权重梯形网络等效电阻的研究
权重梯形网络等效电阻的研究*
邱为钢
(湖州师范学院理学院浙江 湖州313000)
张 萍
(北京师范大学物理学系北京100875)
*国家自然科学基金,项目编号:11275067;浙江省高等学校创新团队,项目编号:T200924;湖州师范学院首届中青年教师卓越教学能力培养计划;浙江省高等学校访问学者教师专业发展项目.
摘 要:权重梯形网络是梯形网络的推广,上、中、下3层各级电阻为等比级数.由电阻的串、并联性质,得到了这个网络N阶等效电阻的递推关系式及计算程序.当权重系数相等时,给出了无穷权重梯形网络等效电阻的解析表达式.
关键词:梯形网络等效电阻权重系数
收稿日期:(2014-08-07)
作者简介:邱为钢(1975-), 男, 博士,副教授,主要从事大学物理的教学和研究.
1引言
把梯形网络电阻看作是一级级的开口形电阻组合,那么,文献[1~4]研究的梯形网络电阻,每一级是相同的.我们可以继续推广这个模型,即每一级开口电阻不再相等,且上、中、下各层电阻前后级成正比关系(权重),而且权重比例系数不同.当级数趋向无穷大时,这个网络的等效电阻如何计算?这就是本文主要研究问题.
2等效电阻递推式
设权重梯形网络电阻的级数为N,等效电阻为RN.每一级的上、中、下层电阻是前一级相应各层电阻的倍数,比例分别为k1,k,k2.最左端的各层电阻分别为r1,r,r2,如图1所示.

图1 权重梯形网络电阻
从最右端的电阻开始往前逐级计算,最右边的一级电阻是
R0=k1Nr1+k2Nr2+kNr
(1)
由电阻的并联关系式,得到第N级电阻与第N-1级电阻的递推关系
(2)
式(2)电阻的迭代公式,很容易用数学软件编程数值计算.数学软件Mathematica的程序为:
R[k1_,k_,k2_,r1_,r_,r2_,N_]:=
理论上当级数N趋向无穷大时,以上程序给出的数值结果就是这个权重梯形网络的等效电阻.但数值计算时,级数N越大,计算时间越大,一般我们取N=100,认为这个值就是等效电阻值.
3权重系数相等时的等效电阻
接下来我们研究电阻的解析性质.当各层电阻的比列系数相同时,即k1=k=k2,式(2)有解析解.设Rn=kN-nPn,式(2)化为

(3)

An=krAn-1+(r1+r2)Bn
(4)
Bn=kAn-1+rBn-1
(5)
如果

(6)
那么就有

(7)

(8)
式(7)除以式(8),计算得到N级梯形网络等效电阻满足的关系式为
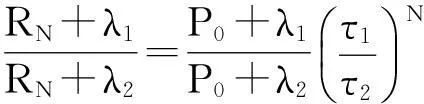
(9)

计算得到式(9)中的各个参数为

(10)
(11)
以及
(12)
式中
4等效电阻方程
接下来我们考虑各层电阻比列系数不同时,无穷梯形网络等效电阻所满足的关系式.设这个无穷等效电阻为R(r1,r2,r,k1,k2,k), 由式(2)取极限,得到

(13)
式(13)就是等效电阻满足的方程,目前看来没有解析解,但当各层电阻的等比系数相同时,可以求解,此时式(13)化为
(14)
由等效电阻的相似性质
R(kr1,kr2,kr,k)=kR(r1,r2,r,k)
(15)
计算得到无穷梯形网络的等效电阻为
(16)
这与式(9)当N趋向于无穷大的极限的结果是一致的. 当比例系数k趋向于1时,式(16)就返回到文献[2]的结果.
5结论
这样,把梯形网络电阻推广到权重梯形网络电阻,得到了等效电阻所满足的关系式.当权重系数相同时,得到了无穷权重梯形网络等效电阻的解析表达式.
参 考 文 献
1江超. 梯形电阻网络的研究. 大学物理, 2000 , 19 (3) :19~22
2陆建隆,谭志中. 关于梯形网络等效电阻的普适研究.大学物理,2001,20 (10) :26~28
3李永安. 梯形网络等效电阻的网络分析. 大学物理,2002 ,21 (12) :9~10
4李永安.梯形网络等效电阻网络分析的再研究. 大学物理,2003 ,22 (10) :12~14
A Study on the Equivalent Resistance of
Weigthed Ladder-shaped Network
Qiu Weigang
(School of Science, HuZhou Teachers College, HuZhou, ZheJiang313000)
Zhang Ping
(Department of Physics,Beijing Normal University,Beijing100875)
Abstract:The weighted ladder-shaped network is a network in which each ladder resistance is a geometric series. The recursion equation of equivalent resistance is derived with a mathematic code. The analytical expression of equivalent resistance is given when the weight coefficients are the same
Key words: ladder-shaped network; equivalent resistance; weigth coefficient

