一系螺旋弹簧动刚度对车辆-轨道耦合振动影响分析

第一作者孙文静女，博士，1989年生

通信作者周劲松男，教授，博士生导师，1969年生

一系螺旋弹簧动刚度对车辆-轨道耦合振动影响分析

孙文静1,2, 宫岛2, 周劲松2, 李卓3

(1.同济大学机械与能源工程学院， 上海201804; 2.同济大学铁道与城市轨道交通研究院， 上海201804;3.北京汽车股份有限公司 汽车研究院， 北京101300)

摘要：建立准确表征一系悬挂轴箱螺旋弹簧波动特性的力学模型，运用动刚度矩阵法求解，研究其对悬挂系统隔振性能影响。结合基于格林函数法的车辆-轨道耦合动力学模型，引入弹簧刚度频变特性，对比分析考虑一系螺旋弹簧频变刚度前后车辆动力学性能之间的差异。结果表明，动刚度矩阵法可以精确求解螺旋弹簧随频率变化的动刚度特性，在一阶模态振动频率后弹簧刚度值呈现103等级的剧烈变化，该结果与有限元模型结果一致；一系螺旋弹簧的动态频率特性导致轮轨激励由车轮至构架的振动位移传递率提高到接近于1，而对车体的振动传递率提高到了10-3左右；在整车车辆-轨道动力学计算中，其对轮轨振动影响较小，但车体与构架出现了较高的高频振动能量峰值。包含一系悬挂动刚度的车辆模型更接近实际，为了降低车辆振动，应尽量提高一系螺旋弹簧自振频率并降低动刚度变化幅值。

关键词：一系悬挂; 螺旋弹簧；动刚度矩阵法; 刚度频变特性; 车辆-轨道耦合振动

基金项目：国家“十二五”科技支撑计划(2011BAG10B01)，中国博士后科学基金(2013M541538)

收稿日期：2013-09-23修改稿收到日期：2014-03-14

中图分类号:U270+1文献标志码：A

Influence of dynamic stiffness of primary suspension on vehicle-track coupled vibration

SUNWen-jing1,2,GONGDao2,ZHOUJin-song2,LIZhuo3(1. School of Mechanical Engineering, Tongji University, Shanghai 201804, China;2. Institute of Railway and Urban Mass Transit, Tongji University, Shanghai 201804, China;3. Beijing Car and Limited by Share Ltd Automobile Research Institute, Beijing 101300, Chin)

Abstract:The dynamic model of helical spring in axle box of primary suspension, which can be solved by using dynamic stiffness matrix method, was established to get its dynamic stiffness for studying the effect of waves propagating in helical spring on the vibration isolation performance of primary suspension. Then, the dynamic stiffness characteristics were introduced into the vehicle-track coupled dynamic model which was then solved with Green’s function method for comparing the dynamic performances between the models with constant stiffness and dynamic stiffness. The results show that the frequency-dependent stiffness can be calculated efficiently with the dynamic stiffness matrix method and the spring stiffness has a thousand-flod dramatic change at the frequency higher than the first modal frequency. This conclusion was verified with the finite element method. This change led to high vibration displacement transmission rate from wheel to bogie at high frequencies, it was shown that it is nearly equal to 1, while the tramission rate from wheel to car body is about 10-3. There are lots of vibration peaks at high frequencies on car body and bogie in vehicle-track coupled dynamic simulation, which are much stronger than those on wheel or rail; the vehicle model including dynamic stiffness of primary suspension spring is more realistic; in order to reduce vehicle vibration, the modal frequency of spring should be raised and the varying of dynamic stiffness amplitude should be as small as possible.

Key words:primary suspension; helical spring; dynamic stiffness matrix method; frequency-dependent dynamic stiffness; vehicle-track coupled vibration

螺旋弹簧是轨道车辆一系悬挂的重要组成部分，其性能直接影响车辆动力学性能，我国部分型号高速列车及和谐号机车出现螺旋弹簧断裂的现象，这表明有必要对车辆螺旋弹簧自身振动及其对高速车辆振动的影响展开深入研究。随着列车速度提高，轮轨激励频率增加，以往动力学分析中，简化的螺旋弹簧线性刚度难以表达其高频振动传递特性。

国外，针对螺旋弹簧的波动效应及振动特性有较多研究，Wittrick[1]将弹簧视为Timoshenko梁建立线性微分方程组，得到了近似解。Mottershead[2]采用特殊有限元法求解振动方程，对于静态问题可以得到精确解。Soroki[3]基于Euler梁理论，采用格林矩阵法与边界条件积分方程，求解弹簧的精确简谐响应，并且分析了无限长弹簧的振动能量传递。符朝兴[4]应用冲击波动理论模拟螺旋弹簧悬架车辆高频振动。张立军[5]利用四端参数法研究螺旋弹簧驻波效应对悬架振动传递特性的影响。刘丽[6]建立中央悬挂弹簧有限元模型，提出采用多自由度系统等效弹簧系统的方法得到动刚度曲线。席德陵等[7-8]对机车车辆上应用的螺旋弹簧进行了特性参数分析、强度计算及测试。但目前，尚无悬挂系统螺旋弹簧动刚度特性对轨道车辆及轨道动力学性能影响的研究。

为此，本研究提出建立准确表征一系悬挂螺旋弹簧波动特性的力学模型，运用动刚度矩阵法进行求解，并采用有限元模型进行对比验证，研究螺旋弹簧波动特性及其对转向架与轮对间更宽频带范围振动传递的影响。结合基于格林函数法的高速车辆-轨道耦合动力学模型，引入弹簧刚度的频变特性，分析其对车辆及轨道振动影响。

1高速车辆轴箱弹簧结构

圆柱螺旋压缩弹簧在各种机械及车辆中的应用十分广泛，轨道车辆上的轴箱弹簧大多采用该种形式，弹簧两端圈应与支撑座有较好的接触，具有较高的工作稳定性且端面磨平。当螺旋弹簧仅在轴线方向承受载荷时，忽略螺旋角影响，简化刚度可由载荷F与变形f的关系得到[9]：

(1)

式中参数的含义如表1所示，上式即用来弹簧设计中确定理论刚度值。

为了提高弹簧的性能，常采用两个或多个直径不同的弹簧同心安装，形成组合弹簧，本文所研究的高速车辆一系轴箱螺旋弹簧即为该并列式组合弹簧。该类型组合弹簧可承受较大载荷，为了避免支撑面的过大扭转和弹簧间相互干扰，弹簧分别做成左旋和右旋，交替安装。组合弹簧的等效刚度为两根弹簧刚度之和：

K=K1+K2

(2)

工作时，两根弹簧的变形量相同，总载荷为与刚度有关的两者载荷之和。

以往，螺旋弹簧往往是以一个简单线性刚度来代替，常用的高速列车一系螺旋钢弹簧在0~20Hz以内的刚度特性几乎与频率无关，为一恒定常数。但在高频区域，应当考虑其变化的动刚度特性对车辆振动产生影响[10]。在多体动力学轨道车辆模型中，通常有两种螺旋弹簧的建模方法，一是采用点到点的力元，仅沿着弹簧作用有轴向力，其二是采用压缩力元，既存在轴向力又存在切向力与力矩。这两种方法都认为与车辆其他结构相比弹簧质量与惯量都非常小，建模时均视为无质量的系统。实际上，轨道车辆上使用的螺旋弹簧其质量体积均较大，随着列车运行速度提高，高频激励条件下悬挂系统的动刚度特性显著，车辆振动传递特性改变。针对以往被忽略的螺旋弹簧动态特性，下节采用动刚度矩阵法求解弹簧解析模型动刚度特性，并采用有限元模型进行验证。

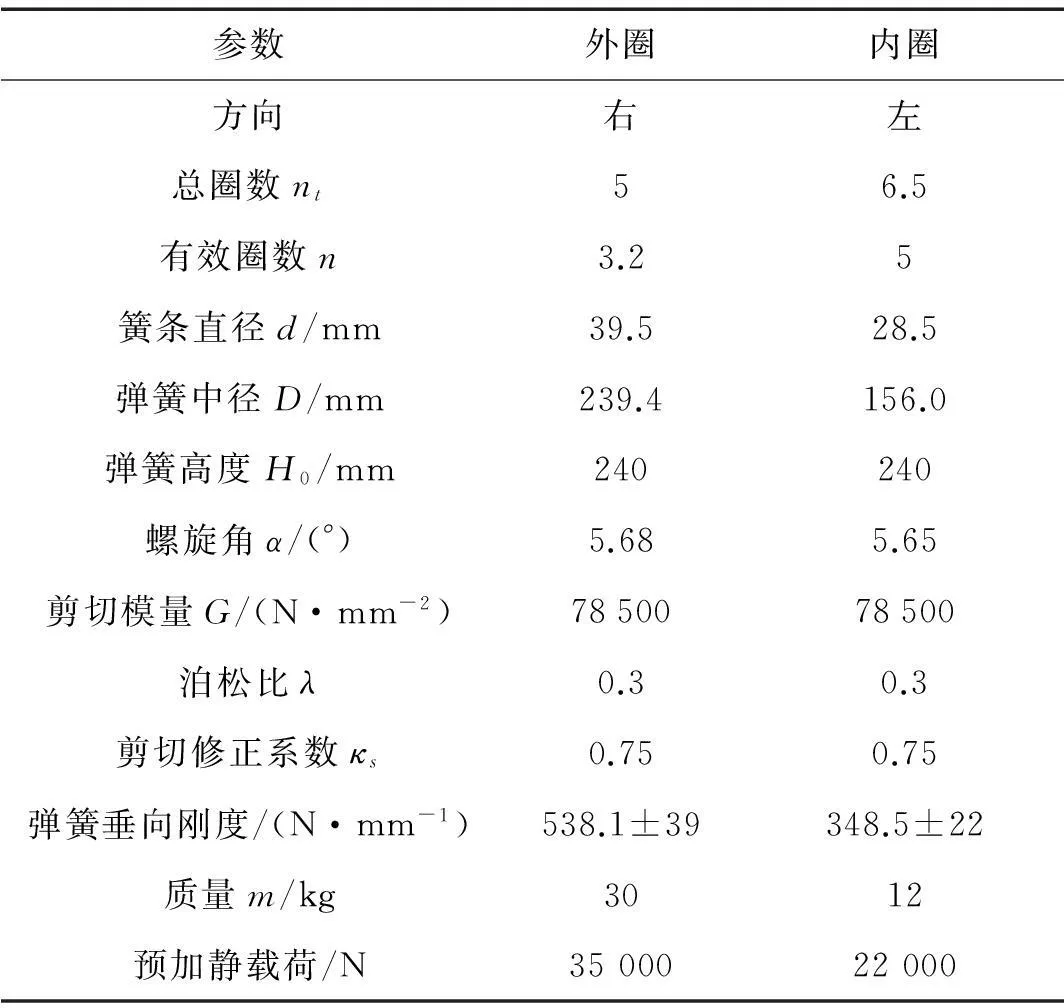
表1　轴箱螺旋弹簧参数

2螺旋弹簧动刚度模型

2.1解析模型

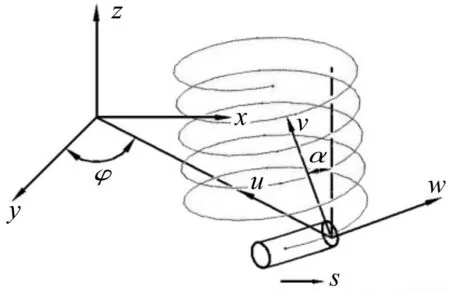
图1　弹簧局部坐标 与整体坐标关系 Fig.1 Co-ordinate system of helical spring

螺旋弹簧的局部坐标与整体坐标系统的关系如图1所示，φ为局部与整体坐标之间转换角，沿着弹簧簧条的坐标为s，α为弹簧螺旋角。

由图1可知坐标转换角φ与簧条位置、螺旋角及弹簧直径的关系如下：

φ=2scosα/D

(3)

依据弹性体计算理论[11]，当螺旋弹簧受到动载荷F作用时，在任意横截面会产生三个方向的力和力矩{P}6×1，并导致三个方向的线性位移和转角{δ}6×1。依据达朗贝尔原理静平衡方程，得到该动力学系统偏微分方程[1]：

(4)

式中，A，B为与弹簧螺旋结构及其材料属性相关的系数矩阵。本文分别考虑螺旋弹簧的自由与施加预载两种工况，两者系数矩阵A，B形式不同，其与所预加的载荷大小有关。

依据式(4)化简得到弹簧载荷与位移间关系式如下：

(5)

依据波动理论，在弹簧中的波可表示为与空间波数k与频率ω相关的叠加[12]，则弹簧的位移和载荷可表示成如下形式：

(6)

式中，k为空间波数，ω为角频率，t为时间。将式(6)代入方程(4)中进行化简得到：

(7)

在给定的频率点ω下，据式(7)，进行特征根计算，得到该方程12个特征根波数ki，同时得到在此波数及频率下的特征向量矩阵[Φ]。

为了得到螺旋弹簧的点刚度及传递刚度值，设定两端的力与位移向量：

(8)

式中，0与L处分别为沿着簧条的弹簧两端点位置，弹簧动刚度即为这两端点处力F与位移U的比值。

依据线性叠加法，弹簧某位置处的位移可表示为由12个不同传递波构成的叠加响应：

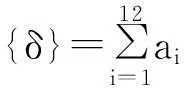
(9)

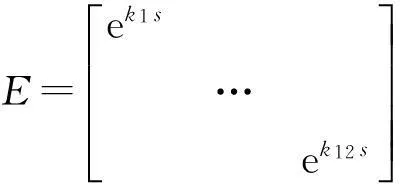
将式(9)求偏微分并代入式(5)中，得到载荷向量：

(10)

依据式(9)及(10)，将s=0，L分别代入，得到式(8)中载荷与位移向量，弹簧刚度矩阵即为：

K=FU-1

(11)

2.2有限元模型

依据表1所列螺旋弹簧结构参数，分别建立内圈与外圈弹簧实体模型，如图2所示。

图2　弹簧的几何模型 Fig.2 Gemetric model of helical springs

采用梁单元对内、外圈弹簧进行单元离散，外圈弹簧有限元模型的节点数为1 235，单元数为1 234，内圈弹簧有限元模型的节点数为1 239，单元数为1 238。约束弹簧顶部中心节点的6个自由度，在弹簧底部中心节点纵向施加1mm幅值的位移正弦激励，并约束其他方向自由度。采用模态叠加法，计算得到0~1000Hz频率范围内，弹簧顶部及底部垂向力随频率变化情况，由于将弹簧视为连续质量单元，因此可得到弹簧点及传递动刚度，定义如下：

(12)

式中，Fb，Ft为在底部作用了幅值xb即1 mm位移激励时，弹簧的底部和顶端的作用力，依据胡克定律，Kp，KT即为弹簧系统的点刚度和传递刚度。

3螺旋弹簧刚度分析结果及讨论

3.1静刚度及模态频率比较

对于内圈与外圈弹簧，采用动刚度矩阵法，有限元计算得到其静刚度值与给出的原始参数进行对比，如表2所示，其中，动刚度矩阵法得到的静刚度值为设定激励频率极低时候的近似静刚度。由表2可见，弹簧自由状态时，解析法与有限元方法计算得到的弹簧静刚度值几乎相等，内外圈弹簧相差分别为0.5%，0.03%，且与给出的原始参数一致。预压缩状态下，内外圈弹簧的静刚度值计算结果均有所下降，但与原始参数差别不大。

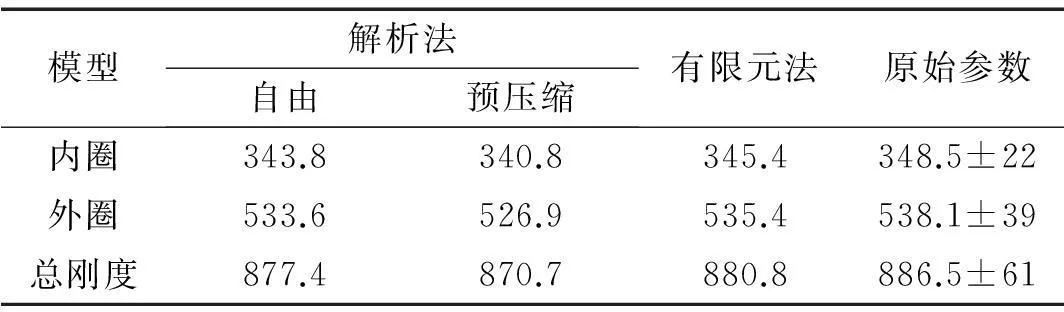
表2　螺旋弹簧静刚度比较(单位：N/mm)

依据弹簧特性，可以得到一端固定，一端自由时，圆柱螺旋压缩弹簧的一阶自振频率的简化算法[9]：

(13)

将圆柱螺旋弹簧简化算法与有限元及动刚度矩阵法计算的弹簧模型一阶模态频率进行比较，如表3所示。由表3可见，动刚度矩阵法、有限元法与简化算法结果吻合较好，其间相差均在1%以下。而在预压缩的状态下，弹簧由于受到压力，导致其产生应力软化效应，从而自振频率会有所减小，这相当于降低了弹簧的刚度，且预压力越大，频率降低的越多，这也是表2中预压缩状态刚度值较小的原因。

表3　螺旋弹簧一阶模态频率比较(单位：Hz)

图3、图4所示为有限元模态分析时，弹簧外圈第一阶与弹簧内圈第十阶的模态振型，虚线表示弹簧原本状态，实线为该阶模态振型最大处。由图可清晰看出弹簧的自身振动特性，其并非无质量恒定刚度系统。

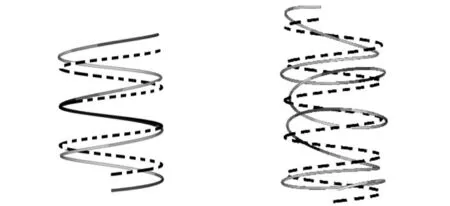
图3 外圈弹簧第一阶模态振型Fig.31stModeshapesofoutspring图4 内圈弹簧第十阶模态振型Fig.410thModeshapeofinnerspring

3.2动刚度频变特性

图5所示为采用动刚度矩阵法与有限元计算得到的弹簧随频率变化的点动刚度曲线。由图可见，在30 Hz以内弹簧保持静刚度特性大小不变，而在接近外圈弹簧一阶自振频率38 Hz，内圈弹簧42 Hz后，由于激励了弹簧的各阶模态振动，不再保持静刚度值不变，而在其附近产生相差几个数量级的剧烈变化，以往采用静刚度值模拟螺旋弹簧显然已不准确。

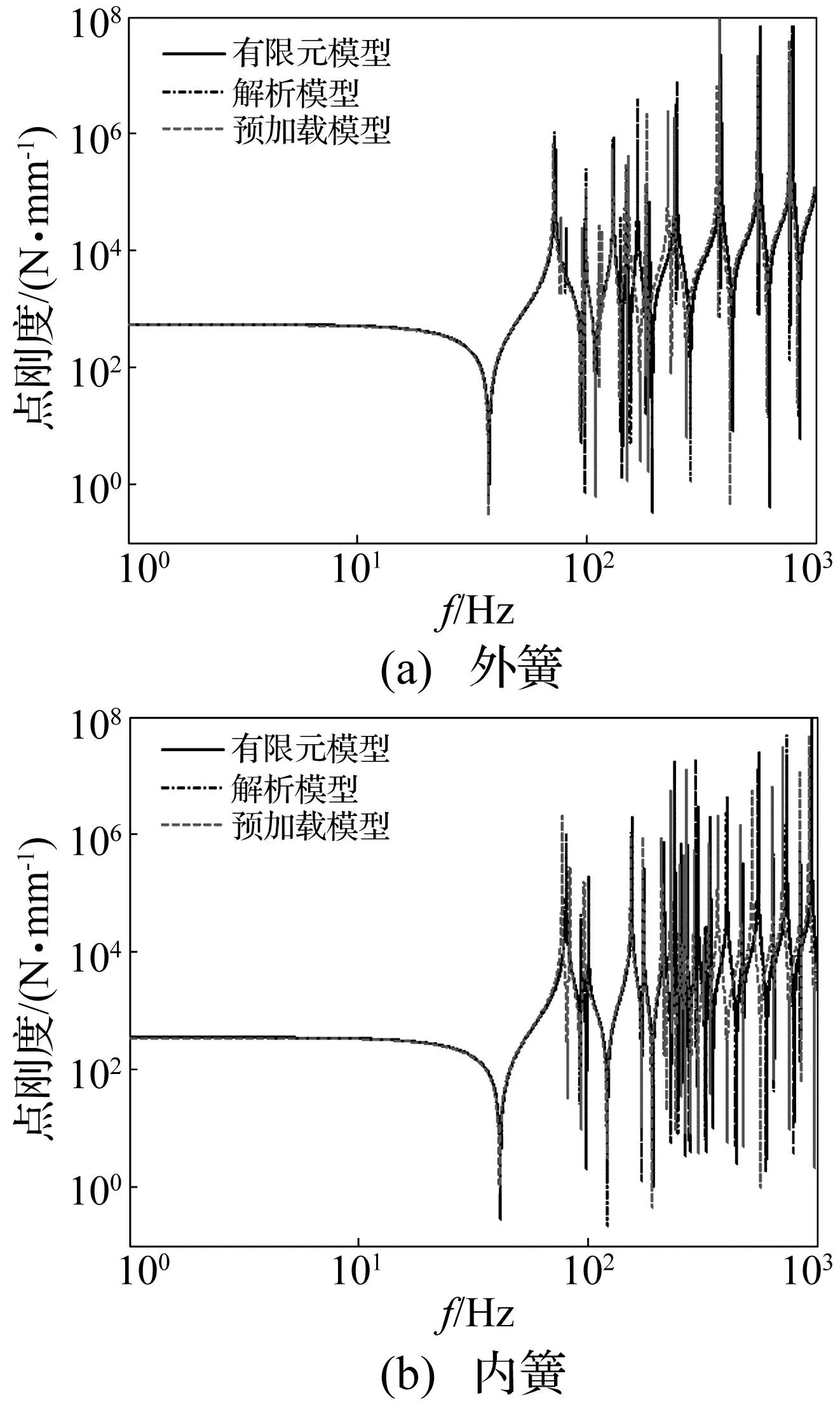
图5　螺旋弹簧点动刚度曲线 Fig.5 Point dynamic stiffness of helical springs

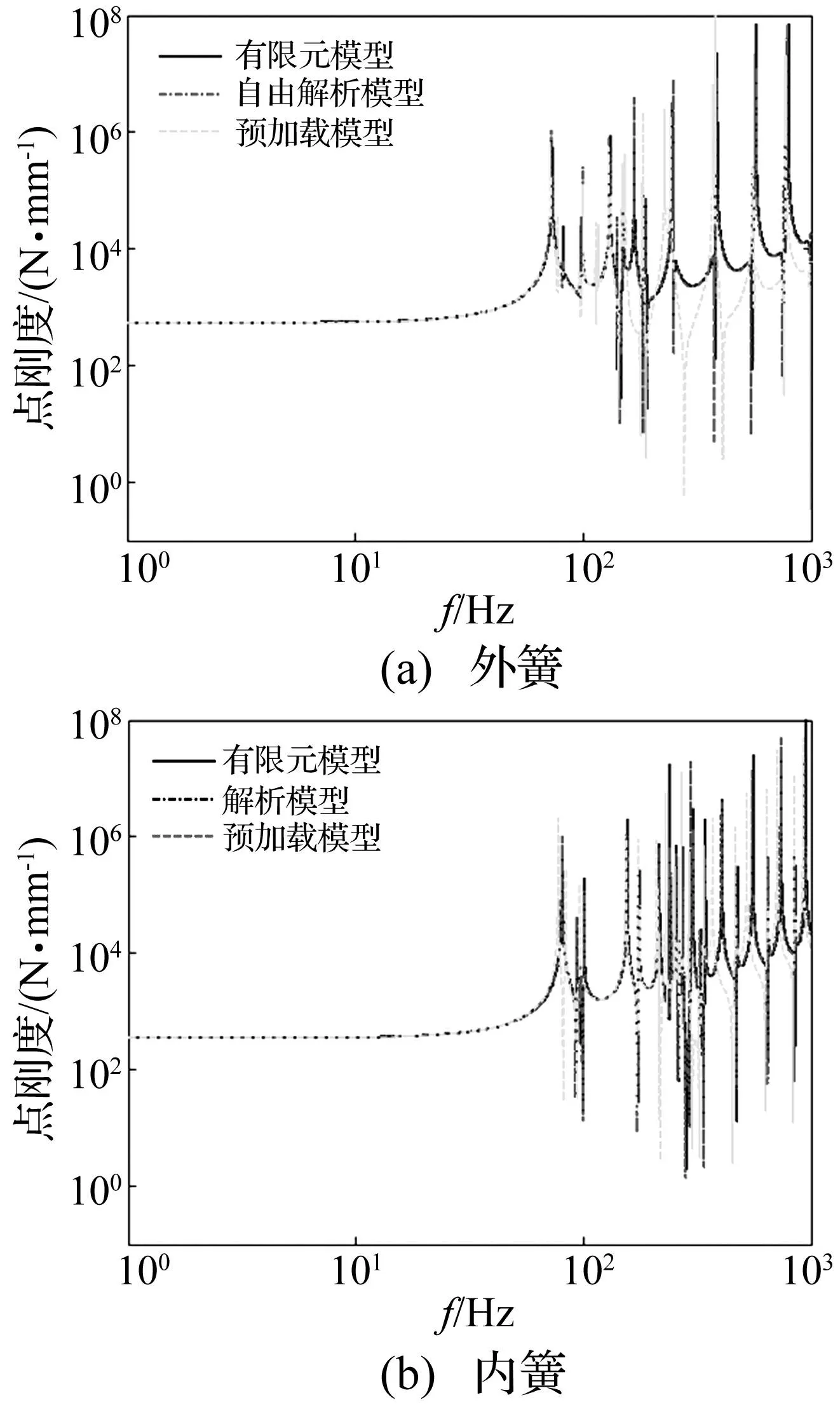
图6　螺旋弹簧传递动刚度曲线 Fig.6 Transfer dynamic stiffness of helical springs

图6所示为内外圈弹簧随频率变化的传递动刚度曲线。由图可见，对于传递动刚度曲线，与点刚度不同在高于70 Hz后弹簧传递刚度值大小产生剧烈变化。同时从图5、图6中看出，解析法与有限元法的差值较小，且由于弹簧内圈与外圈相比，其直径较小圈数较多，在1 000 Hz以内模态阶数更多，刚度值的变化更为频繁密集。并且比较了自由与预压缩状态下的弹簧频变刚度特性，由图5、6可见，预压缩状态下弹簧模态频率有所降低，刚度值略有下降，这是由于弹簧受到了正压力作用导致的。由于预压缩工况下的弹簧更接近于实际工作条件，因而在下节计算中均采用该动刚度计算结果。

4车辆-轨道耦合振动影响分析

为了分析一系悬挂系统螺旋弹簧的动刚度特性对车辆及轨道动力学性能的影响，首先采用简化单轮车辆模型，分析一系弹簧动刚度对车轮至转向架及车体之间振动传递特性影响，而后结合车辆-轨道耦合动力学模型，将螺旋弹簧刚度的频变特性加入整车系统，对比分析静刚度与动刚度一系螺旋弹簧的轨道车辆动力学性能之间的差异。

4.1螺旋弹簧振动传递特性分析

为了了解弹簧动刚度对车辆结构振动传递的影响，建立单轮车辆模型，如图7所示。

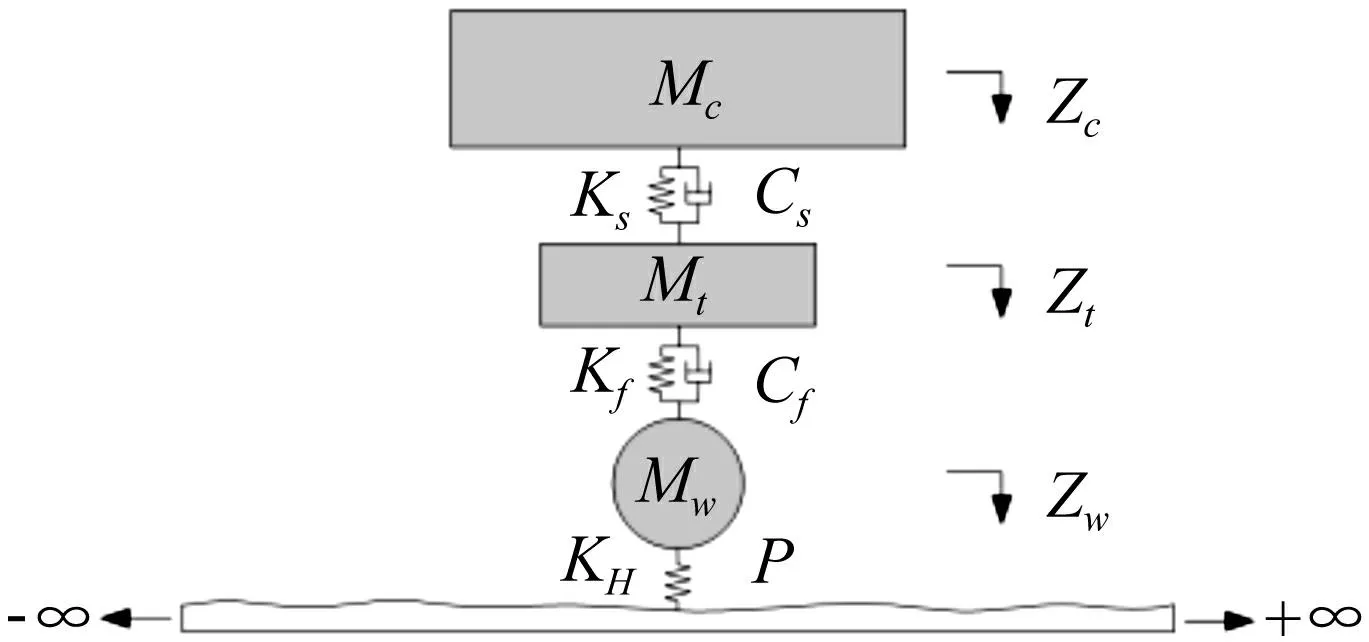
图7　单轮系统模型 Fig.7 Vehicle model of 1 wheel

传统动力学模型中考虑了车体，构架及车轮的垂向自由度zc，zt，zw，Mc，Mt，Mw为车体、构架和车轮质量，ks，cs为车辆系统二系悬挂系统刚度、阻尼，kf，cf为一系悬挂静刚度及阻尼，P为轮轨间作用力，则其运动微分方程为：

(14)

考虑一系弹簧动刚度及橡胶垫阻尼特性，阻尼以损失因子形式η表示在复刚度中：

(15)

式中，Kp*，Kt*为包含橡胶垫阻尼特性的螺旋弹簧点刚度及传递刚度值。得到包含动刚度特性的构架与车轮的动力学方程：

(16)

图8~图9所示为车速250 km/h时，采用一系悬挂静刚度及动刚度模型计算得到的车轮至转向架及车体的振动位移传递率。可以看到，静刚度车辆的车体与构架在整个频段均保持较小的振动传递率，螺旋弹簧起到较好的隔振作用，由于一系悬挂弹簧的动刚度特性，在较高频处导致车体与构架的振动传递率明显增大，显著恶化了车辆系统高频处的振动品质，对于转向架的影响尤为剧烈。

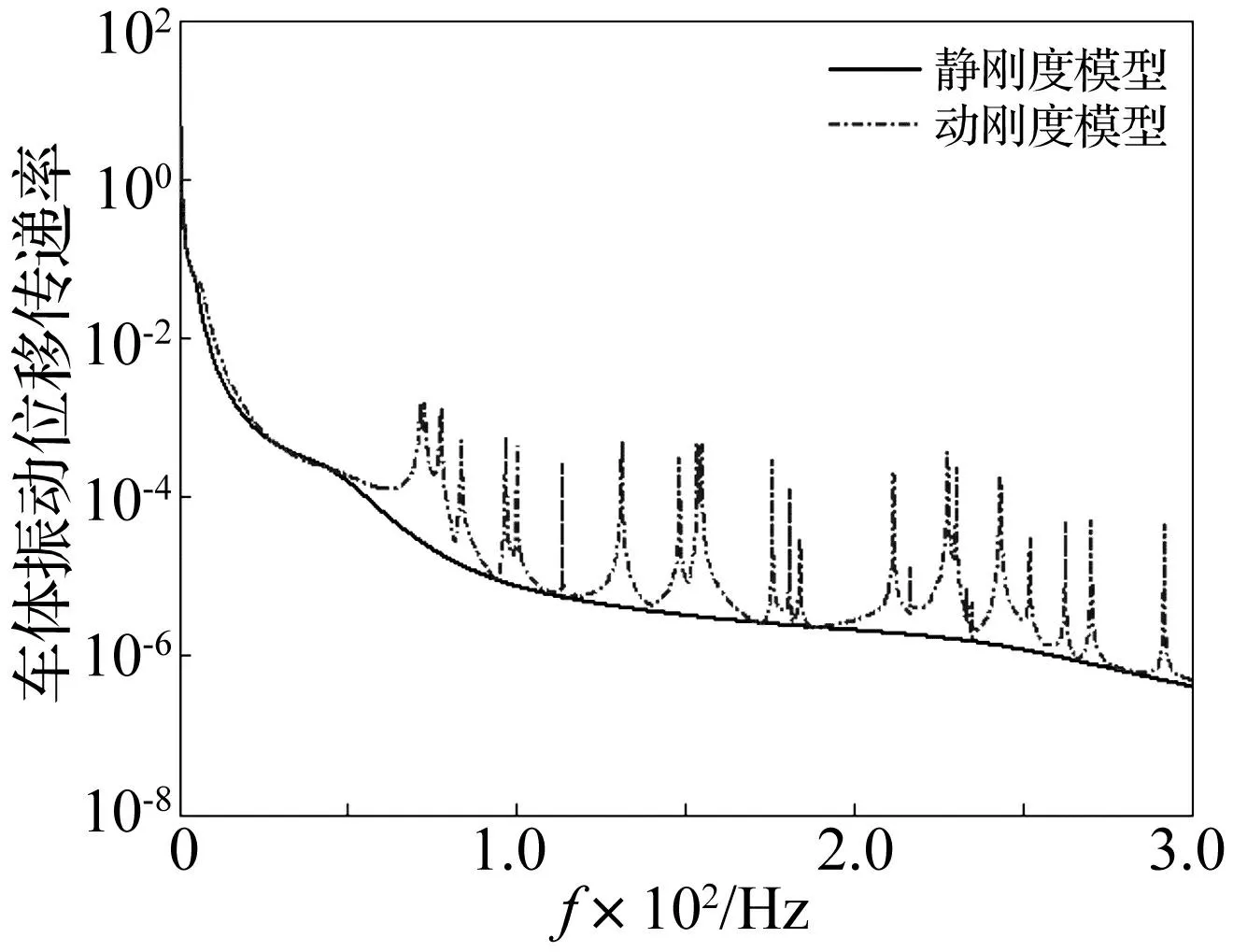
图8　车体振动位移传递率 Fig.8 Displacement transmissibility at car body

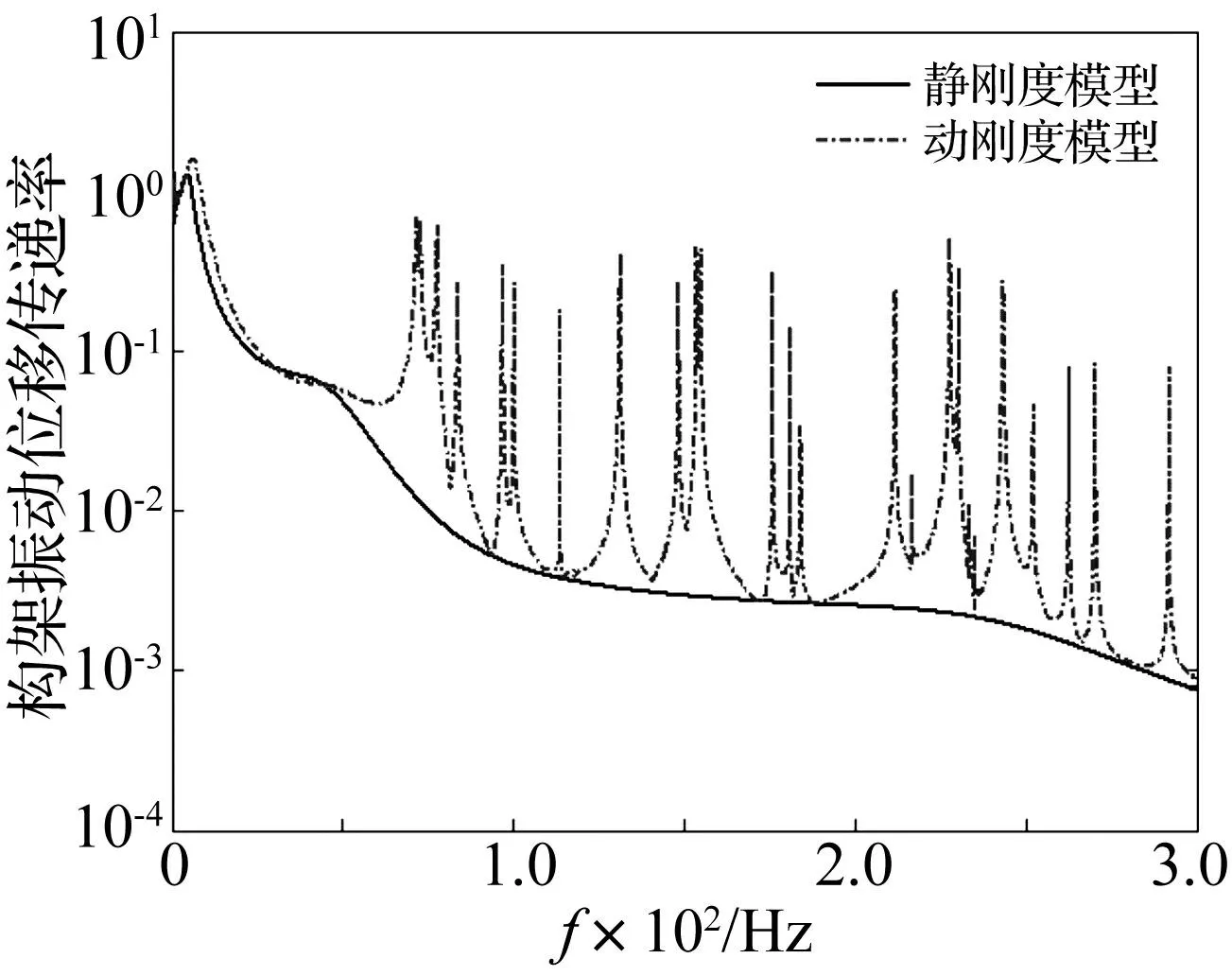
图9　转向架振动位移传递率 Fig.9 Displacement transmissibility at bogie

4.2车辆-轨道耦合动力学影响

4.2.1包含一系螺旋弹簧动刚度特性的车辆-轨道耦合动力学系统

由于一系悬挂系统主要为轴箱弹簧与液压减振器构成的刚度阻尼系统，往下连接轮对，往上连接转向架系统，因而在车辆运行过程中起着十分重要的作用，直接影响车辆的运行安全性及其振动品质。上节采用了简化单轮模型分析了其对振动传递的影响，本节采用动刚度矩阵法计算得到的动刚度曲线对原本的定刚度值进行替换，对整车车辆-轨道耦合动力学系统进行计算，得到其动态特性对整个车辆及轨道系统动力学性能影响。

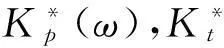
(17)

式中，[M]、[C]分别为车辆系统质量、阻尼矩阵，[Kd]即为包含一系动刚度特性的系统刚度矩阵，{P}为轮轨力向量。

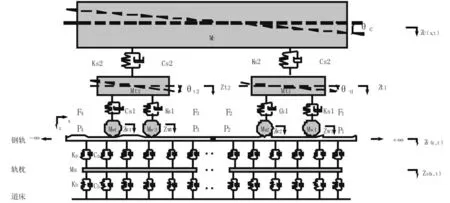
图10　车辆-轨道耦合动力学模型 Fig.10 Vehicle-track coupled dynamic model

如图10所示，轨道视为轨枕道床双层弹簧阻尼连续支撑的弹性钢轨Timoshenko梁系统，考虑钢轨垂向位移zr(x,t)及转动自由度φr(x,t)，建立包含钢轨弹性的轨道系统模型，mr为单位长度轨道质量，E为弹性模量，G为剪切模量，ρ为密度，κ为Timoshenko梁剪切修正系数，A为截面面积，I为轴惯性矩，x，t分别为轨道纵向位置及时间变量，钢轨振动偏微分方程为：

(18)

κGAφr(x,t)=0

(19)

式中，Frs为轨枕对钢轨的作用力，Pj为轮轨力，δ(x-xj)为轮轨接触位置函数。采用格林函数法[13]对轨道系统进行求解，车辆与轨道系统通过线性接触弹簧相互作用[14]。

4.2.2车辆-轨道随机振动响应比较

车速为250 km/h，轮轨激励输入为高速低干扰轨道谱[15]，将采用静刚度值的螺旋弹簧与包含频变刚度特性的高速车辆-轨道耦合动力学振动响应进行比较。图11~图13所示为车轮、钢轨振动加速度及轮轨垂向力功率谱结果，从图中可以看出随着一系螺旋弹簧的动刚度特性在38 Hz之后的剧烈变化，与静刚度模型相比轮轨振动有波动，且集中在弹簧的前几阶自振频率处。由于轮轨高频处的振动是由轨道占主要成分，其不与一系弹簧直接连接，因而动刚度特性对轮轨高频振动影响不大。

图11 车轮振动加速度功率谱Fig.11Vibrationacc.PSDsofwheel图12 钢轨振动加速度功率谱Fig.12Vibrationacc.PSDsofrail图13 轮轨垂向力功率谱Fig.13VerticalcontactforcePSDs

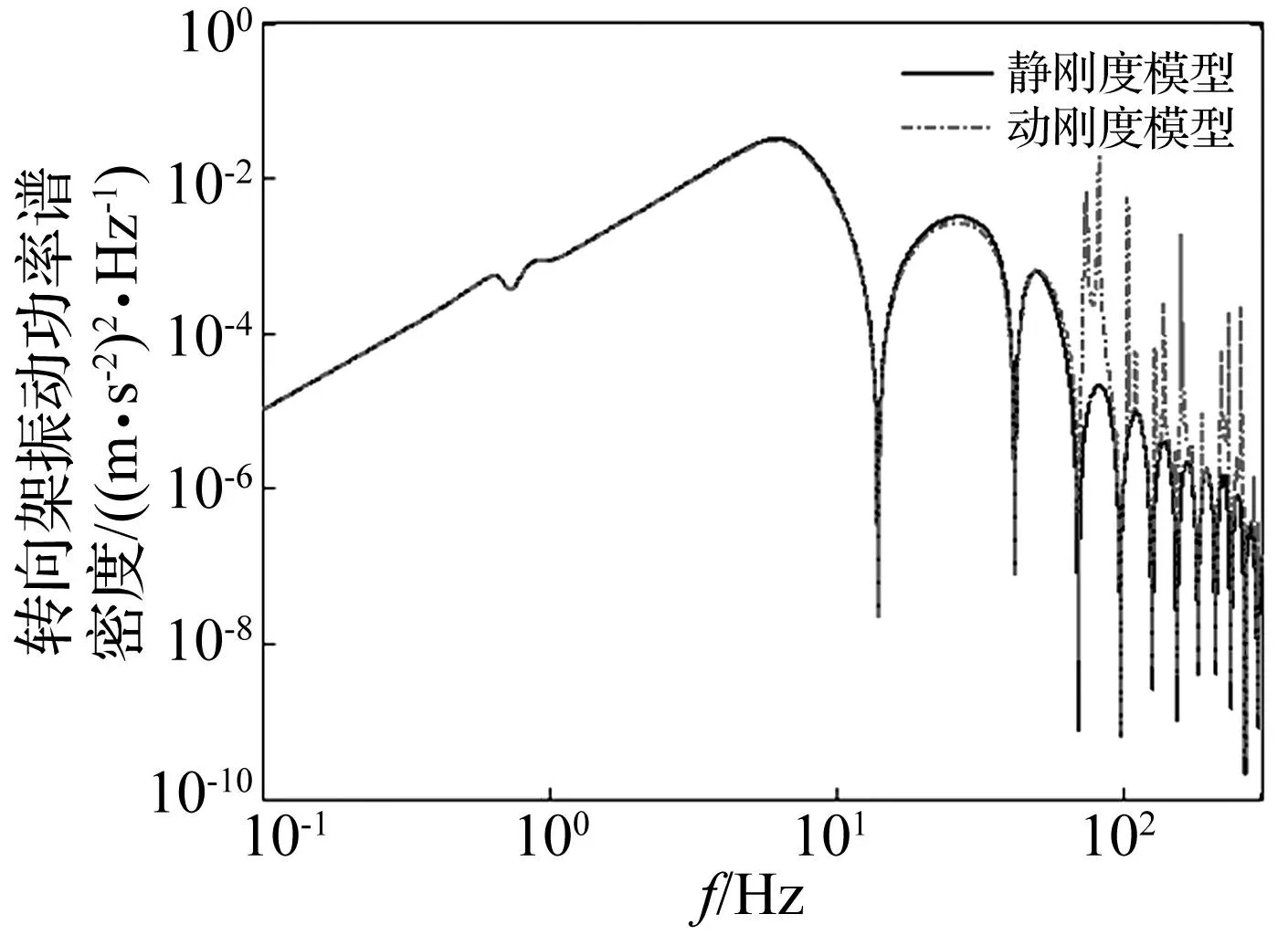
图14　转向架振动加速度功率谱 Fig.14 Vibration acc. PSDs of bogie

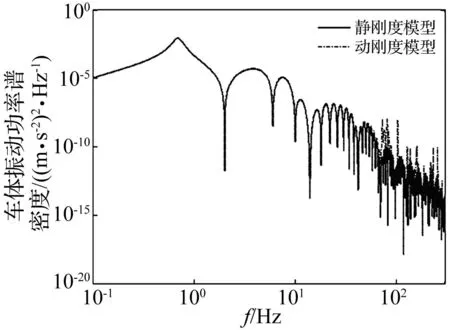
图15　车体中心振动加速度功率谱 Fig.15 Vibration acc. PSDs of car body center

图14-图15所示为构架及车体振动加速度功率谱，由图可见，随着螺旋弹簧动刚度数值的变化，构架和车体的高频振动显著加剧，出现多个峰值，与轮轨系统响应相比，螺旋弹簧对车体及构架的影响更大。可见，一系螺旋弹簧的动刚度频变特性对于车体及构架振动有不利影响，悬挂系统轴箱弹簧作为车辆重要的减振元件一直认为是用于车辆结构高频减振的重要手段，在考虑了弹簧真实动刚度特性后发现，其显然没有达到理想中的高频隔振效果。

5结论

考虑车辆一系悬挂螺旋弹簧的质量及具体结构，采用动刚度矩阵法对其进行动刚度特性计算，并分析了其对高速车辆-轨道耦合系统振动的影响。可以得出以下结论：

(1)采用动刚度矩阵法可以准确求解螺旋弹簧力学模型，得到其振动模态及动刚度频变特性。针对本文所研究的高速车辆一系轴箱螺旋弹簧，预压缩状态下其内外圈第一阶自振频率分别为41.4 Hz、37.5 Hz，相比自由状态其模态频率略有降低，在此频率之后，动刚度相比静刚度值一直保持着103等级的剧烈波动；

(2)在螺旋弹簧的自振频率处，其动刚度特性显著提高了车轮至上方构架及车体的振动传递率。对于构架振动位移传递率在较宽频率范围内均接近于1，由于二系悬挂的进一步隔振作用，对于车体的振动传递相比构架来说有所降低，在10-3左右；

(3)频变动刚度值使得螺旋弹簧悬挂系统在高频处隔振性能降低，其对轮轨振动影响较小，而车体与构架在50 Hz之后的整体高频振动能量显著增大。

本文所研究的车辆是最大运行速度为350 km/h的动车组，轮轨激励频带宽，一系螺旋弹簧频变刚度的影响不可忽略。且在轮轨系统中，车轮或轨道缺陷如车轮不圆、轨道波磨等一直存在，其引起的系统激励频率更高且与弹簧模态频率区间是存在重合的，此时系统会产生较大的共振峰值，极有可能恶化弹簧自身以及轮对至车体、构架的振动。在进行高速车辆动力学计算分析时，能够准确获得一系螺旋弹簧的动态刚度变化，并在动力学计算时考虑这一动态特性，则能够准确的模拟实际工况，为车辆的设计做出更加准确的动力学性能评估。包含一系螺旋弹簧动刚度的系统动力学模型，可为今后车辆减振及弹簧疲劳研究提供一定依据。

参考文献

[1]Wittrick W H. On elastic wave propagation in helical springs [J]. International Journal of Mechanical Sciences, 1966, 8(1): 25-47.

[2]Mottershead J E. The large displacements and dynamic stability of springs using helical finite elements [J]. International Journal of Mechanical Sciences, 1982, 24(9): 547-558.

[3]Sorokin S V. The Green’s matrix and the boundary integral equations for analysis of time-harmonic dynamics of elastic helical springs [J]. The Journal of the Acoustical Society of America, 2011, 129(3): 1315-1323.

[4]符朝兴, 王秀伦. 螺旋弹簧悬架车辆振动的波动理论建模及频响分析[J]. 机械工程学报, 2005, 41(5): 54-59.

FU Chao-xing, WANG Xiu-lun. Wave theory modeling of vehicle vibration and its frequency response analysis of helical spring suspension [J]. Chinese Journal of Mechanical Engineering, 2005, 41(5): 54-59.

[5]张立军, 余卓平. 螺旋弹簧的驻波效应对悬架隔振特性的影响[J]. 振动与冲击， 2002, 21(2): 45-47.

ZHANG Li-jun, YU Zhuo-ping. The influence of spiral spring’s standing wave effect on the automotive suspension vibration isolation characteristics [J]. Journal of Vibration and Shock, 2002, 21(2): 45-47.

[6]刘丽, 张卫华. 金属弹簧刚度频变分析及等效算法[J]. 交通运输工程学报, 2007, 7(5): 24-27.

LIU Li, ZHANG Wei-hua.Frequency variety analysis and equivalent algorithm of metal spring stiffness. Journal of Traffic and Transportation Engineering, 2007, 7(5): 24-27.

[7]席德陵, 龚积球, 张定贤等. 高圆簧 (加橡胶垫) 稳定性计算的研究[J]. 铁道学报, 1992, 14(4): 1-7.

XI De-ling, GONG Ji-qiu, Zhang Ding-xian, et al. A study on the stability calculation for flexicoil springs with rubber pads [J]. Journal of the China Railway Society, 1992, 14(4): 1-7.

[8]佘雷兵, 龚积球. 高柔度圆弹簧 (加橡胶垫) 的稳定性研究[J]. 中国铁道科学, 1991, 1(991): 2.

YU Lei-bing, GONG Ji-qiu. A study of the stability of flexicoil springs with rubber layer [J]. China Railway Science, 1991, 1(991): 2.

[9]张英会,刘辉航，王德成. 弹簧手册[M]. 北京：机械工业出版社, 2008.

[10]Bruni S, Vinolas J, Berg M, et al. Modelling of suspension components in a rail vehicle dynamics context[J]. Vehicle System Dynamics, 2011, 49(7): 1021-1072.

[11]Timoshenko S P, Gere J M. Theory of elastic stability [M]. Courier Dover Publications, 2012.

[12]Lee J, Thompson D J. Dynamic stiffness formulation, free vibration and wave motion of helical springs [J]. Journal of Sound and Vibration, 2001, 239(2): 297-320.

[13]Sun W, Zhou J, Thompson D, et al. Vertical random vibration analysis of vehicle-track coupled system using Green’s function method [J]. Vehicle System Dynamics, 2014, 52(3): 362-389.

[14]Wu T X, Thompson D J. Vibration analysis of railway track with multiple wheels on the rail [J]. Journal of Sound and Vibration,2001, 239: 69-97.

[15]周劲松. 铁道车辆振动与控制[M]. 北京：中国铁道出版社,2012.