人工中耳悬浮式压电振子的优化设计

第一作者田佳彬男，博士生，1986年生

通信作者饶柱石男，教授，博士生导师，1962年生

人工中耳悬浮式压电振子的优化设计

田佳彬， 饶柱石， 塔娜， 许立富

(上海交通大学机械系统与振动国家重点实验室，上海200240)

摘要：为了优化人工中耳悬浮式压电振子的植入效果，设计了一种位移放大结构用于改善振子的输出特性。首先采用微CT扫描和逆向成型技术建立了包括外耳道、中耳和简化耳蜗的人耳有限元模型，通过与文献的实验数据比对验证模型的有效性。然后建立人耳与悬浮振子的耦合力学模型，通过有限元的耦合场分析研究加入位移放大结构前后的人工中耳植入效果。研究结果表明，采用位移放大结构后，振子于中高频段的等效声压级得到明显提升，可以有效降低压电振子的功耗。

关键词：人工中耳；压电振子；有限元建模；位移放大结构

基金项目：国家自然科学

收稿日期：2013-11-08修改稿收到日期：2014-04-03

中图分类号:TH785文献标志码：A

Optimal design of a floating mass type piezoelectric actuator for implantable middle ear hearing devices

TIANJia-bin,RAOZhu-shi,TANa,XULi-fu(State Key Laboratory of Mechanical System and Vibration, Shanghai Jiaotong University, Shanghai 200240, China)

Abstract:To optimize the implant performance of a floating mass type piezoelectric actuator for implantable hearing devices, a displacement amplifier was designed to improve the output characteristics of the actuator. A finite element model of human ear consisting of the external ear canal, middle ear and simplified cochlea was constructed via micro-computer tomography imaging and the technique of reverse engineering. The validity of the model was verified by comparing the model-derived results with experimental data from reference. Then an ear-actuator coupled mechanical model was developed, and the multi-field coupling was considered to study the implant performance of the actuator before and after the displacement amplifier was added. The results showed that the adoption of displacement amplifier can increase the equivalent sound pressure level of the actuator in the middle and high frequency ranges, and the power consumption can effectively be reduced at the same time.

Key words:implantable hearing devices; piezoelectric actuator; finite element modeling; displacement amplifier

近年来，人工中耳作为感音神经性听力损伤的治疗手段已经取得了较大的发展。与传统助听器的声激励不同，人工中耳是将外界的声信号转化成机械信号后直接激励听骨链，因此具有负反馈小，语音清晰度高和高频增益强等特点[1]。人工中耳按其激励源的不同可以分为电磁式和压电式，按其植入方式的不同则分为部分植入式和全植入式。其中，由于压电式较电磁式具有频带宽，制造成本低以及抗电磁干扰等优点，近年来已有多篇文献对惯性压电式人工中耳的植入特性进行了研究[2-3]。同时，人工中耳作为便携式设备，电源续航能力是一个非常重要的参数，特别是对于全植入式人工中耳，尽管可以通过皮肤进行再次充电，但仍然需要几年更换一次。因此，如何降低功耗成为人工中耳的进一步应用中亟待解决的问题。

对于压电式人工中耳而言，现阶段普遍采用压电叠堆的形式作为振子的基本构成[4-5]，这主要是由于压电叠堆具有输出力大，共振频率高等特点，这将非常有利于感音神经性听力损伤的高频补偿。但压电叠堆也有其自身的局限性，即输出位移较小[6]，虽然可以通过增加压电叠堆的层数或激励电压的方式来增大输出位移，但这都将导致压电振子功耗的增加。另一方面，人工中耳作为微型设备植入到人体的中耳腔之中，这会受到人耳本身微小生理尺寸的限制[7]，这也决定了不可能采用过多的压电叠堆层数来增加输出位移。Niezrecki等提出了称之为Moonie的位移放大方案用于改善压电叠堆的输出特性[8]，压电叠堆的位移形变方向与输出形变方向垂直正交，具有较为良好的位移放大效果，并且在增大输出位移的同时不会增加系统的功耗。本文采用Moonie方案对悬浮振子的结构进行了优化设计，并通过计算等效外耳道声压级和功耗的大小对优化的实际效果进行评价。

准确地评价人工中耳的具体植入效果，需要对人耳的传声特性和生物力学机理具有详细的把握。有限单元法作为一种数值方法，不仅可以对人耳复杂的几何形态，超微型的结构特征和非同质的材料特性进行模拟，而且可以应用多场耦合技术对人耳生物力学中所伴随的声固耦合，流固耦合等复杂机理进行研究，从而更加真实地模拟人耳的传声特性。已有相关学者基于中耳的有限元模型对人工中耳的植入特性进行研究[9-11]，但其中耳蜗对于中耳的作用被简化成弹簧和阻尼，这与实验测量的耳蜗输入阻抗并不完全吻合[12-13]。为此，本研究利用高精度的微CT扫描和逆向成型技术构建了人体外耳道和中耳的几何模型与有限元模型，并建立了具有真实大小的耳蜗模型。在此基础上，利用力电耦合方法构建了悬浮振子与人耳耦合的力学模型，通过计算加入位移放大结构前后的人耳输出参数，对等效外耳道声压级，功耗等性能指标进行了综合评价。本文的研究将有利于进一步完善人工中耳的结构设计。

1方法

1.1人耳有限元模型的建立

采用新鲜的人体颞骨标本，应用微CT扫描仪(GE Healthcare，eXplore Locus SP)获得882张医疗影像图片，扫描层的厚度为43.5 μm。利用Simpleware软件(Simpleware公司，英国)对上述图片进行逆向成型，获得外耳道和中耳的三维几何模型。通过有限元软件Abaqus进行网格的划分，获得人体外耳道和中耳的网格模型，其中，鼓膜划分成804个壳单元，外耳道气体和中耳结构均为四面体单元，单元数分别为22 366和48 043。耳蜗采用非螺旋状的，充满液体的双腔导管模型，包括前庭阶、鼓阶、基底膜和卵圆窗，这一简化模型已在多篇文献中应用于耳蜗力学的研究[14-15]。基底膜的尺寸由底部的厚度7.5μm和宽度150μm线性变化到顶部的厚度2.5 μm和宽度500 μm[16]，并划分成482个壳单元，前庭阶和鼓阶的液体容积分别为92.781 μL和93.270 μL，采用六面体单元进行网格的划分，单元数分别为17 577和13 802。最终建立的人耳有限元模型如图1所示。其中，为了显示耳蜗内部的基底膜结构，图1中将耳蜗流体设置成半透明的形式。

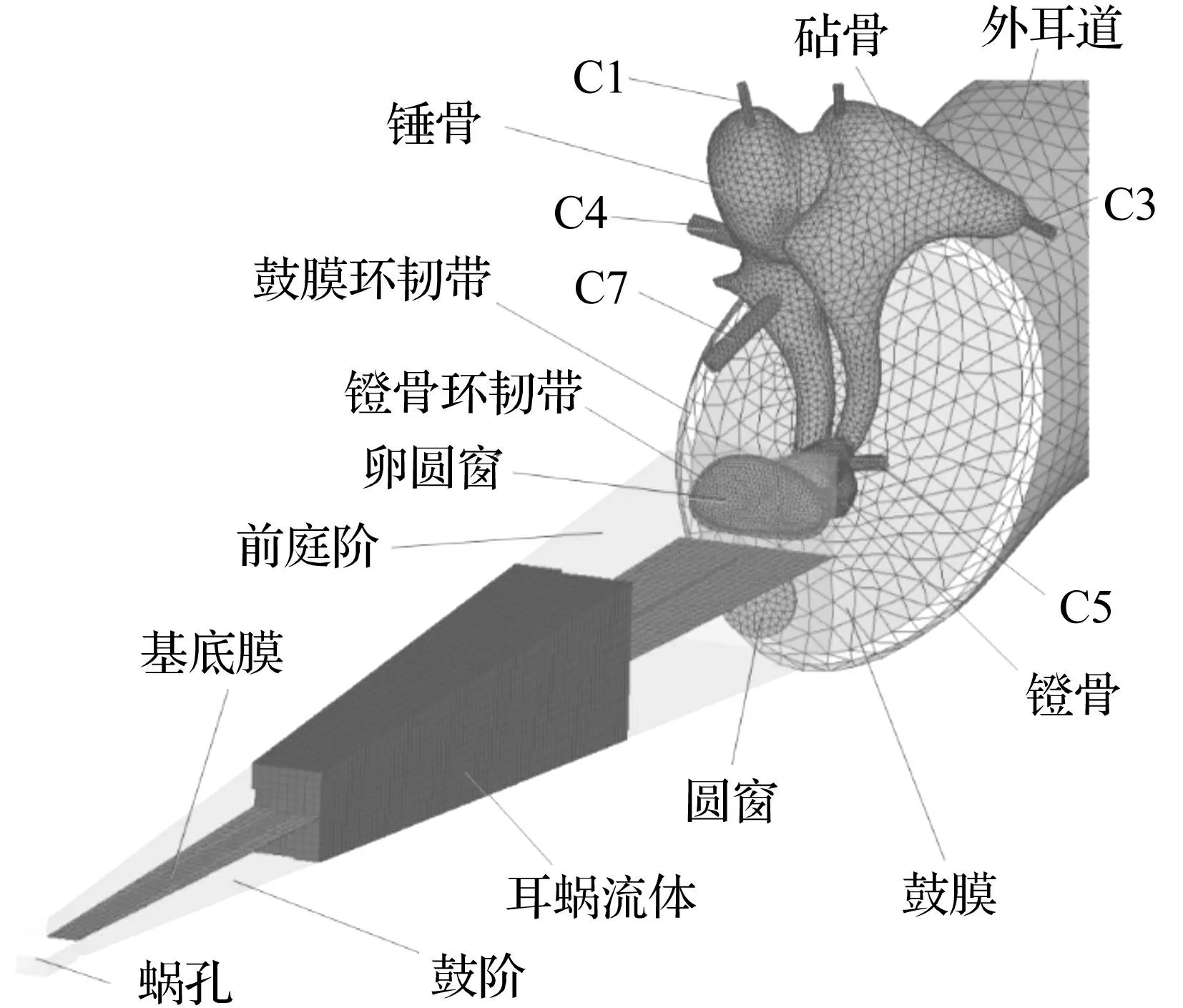
图1　人耳有限元模型 Fig.1 Finite element model of the human ear

人耳力学模型的材料参数分为外耳道气体、中耳部分和内耳部分，其中，外耳道气体的体积模量与密度分别取为0.142 MPa和1.21 kg/m3。中耳听骨链的材料参数主要参考于文献[17]，最终确定的鼓膜、中耳韧带和肌腱、听骨链的材料属性如表1所示。中耳结构的泊松比均为0.3，瑞利阻尼系数取为α=0 s-1，β=0.75×10-4s，边界条件为所有韧带和肌腱的端部固支。内耳部分前庭阶和鼓阶流体的材料特性取为与水相同，即体积模量与密度分别为2 250 MPa和1 000 kg/m3。研究表明，耳蜗基底膜具有沿长度方向刚度渐变的特性[18]，为此，将基底膜的杨氏模量设定为从底部的40 MPa线性减小中间的15 MPa，再依次线性减小到顶部的3MPa，其瑞利阻尼系数取为α=0 s-1，β=0.1×10-3s。

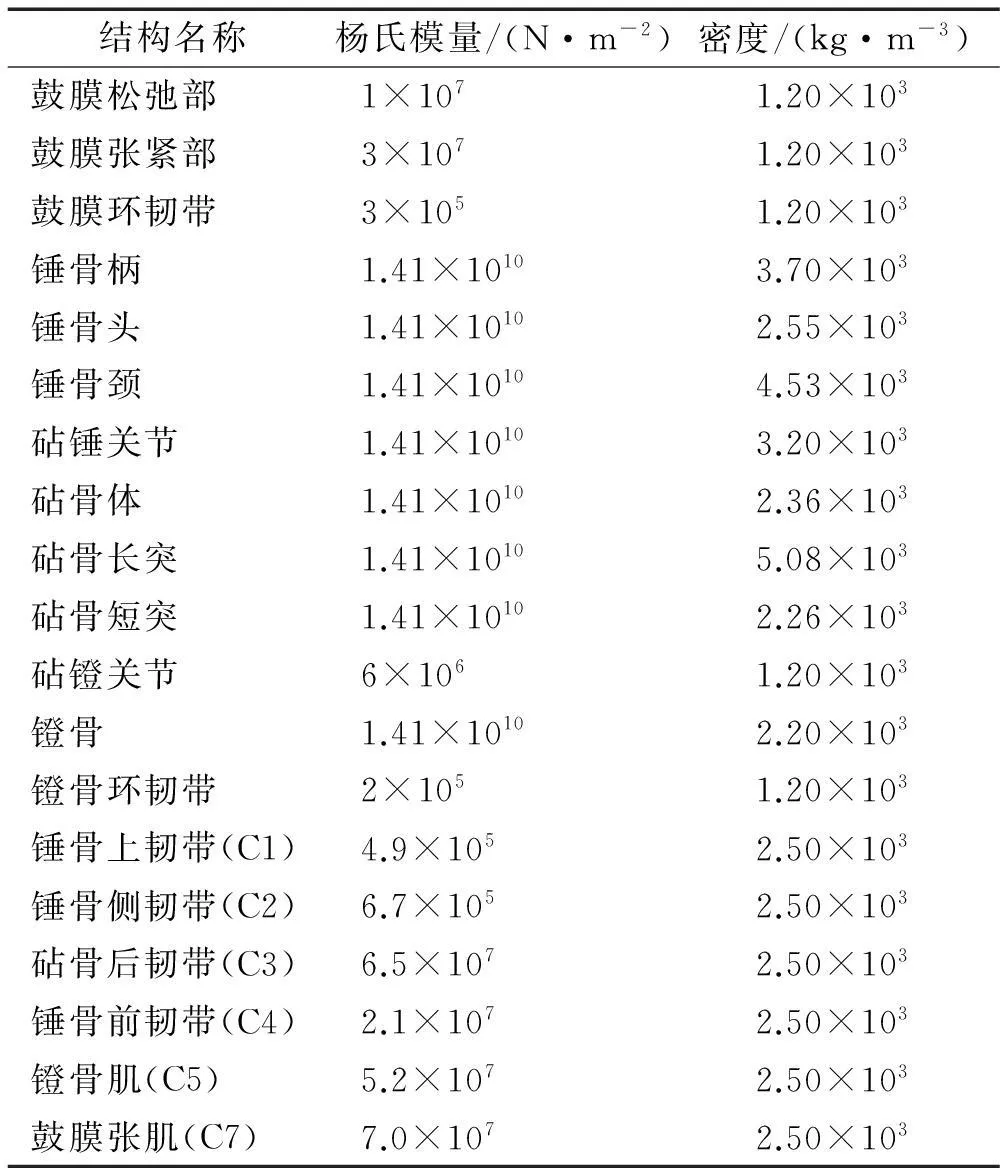
表1　人耳有限元模型材料参数

人耳的动力学模型中，包含了外耳道气体、中耳固体、耳蜗流体和基底膜等结构的多场耦合，本研究中，通过定义流固耦合面来实现流体压力的法向梯度与结构力之间的相互传导，完成人耳系统中流体内边界的设定。流固耦合面包括以下的几个部分：外耳道气体与鼓膜外侧面间的耦合，镫骨底板表面与耳蜗流体的耦合，圆窗与耳蜗流体的耦合，耳蜗隔膜(包含基底膜)两侧与前庭阶和鼓阶流体的耦合。同时，系统的流体外边界设定通过如下的方式实现：外耳道气体毗邻耳道壁面的流体单元表面，以及耳蜗流体毗邻耳蜗骨壁的流体单元表面，定义成Wall边界，即流体压力的法向梯度为零，外耳道入口处的流体单元表面则加载固定幅值的压力载荷，用于模拟正常人耳的声激励。

1.2位移放大结构设计

Monnie位移放大方案如图2所示的结构，由上下两个端盖围成腔体状，压电叠堆置于放大结构的内部。如图2(a)中所示，当压电叠堆产生大小为2Δx的位移形变量时，两个端盖的顶部将会在垂直方向上产生大小为2Δy的位移量。两个位移量之间可以表达成如下关系：

Δy=GΔx

(1)

式中:G为位移放大倍数，其大小与结构的尺寸相关，可通过如下的简化表达式[19]进行计算：

G=L/2h

(2)

式中，L为放大结构腔体的长度，h为腔体的高度。

本研究中，L等于压电叠堆的长度，大小为1.8mm，由于植入位置中耳腔空间的限制，最终确定的位移放大倍数为5，因此得到腔体的高度尺寸为h=0.18mm。

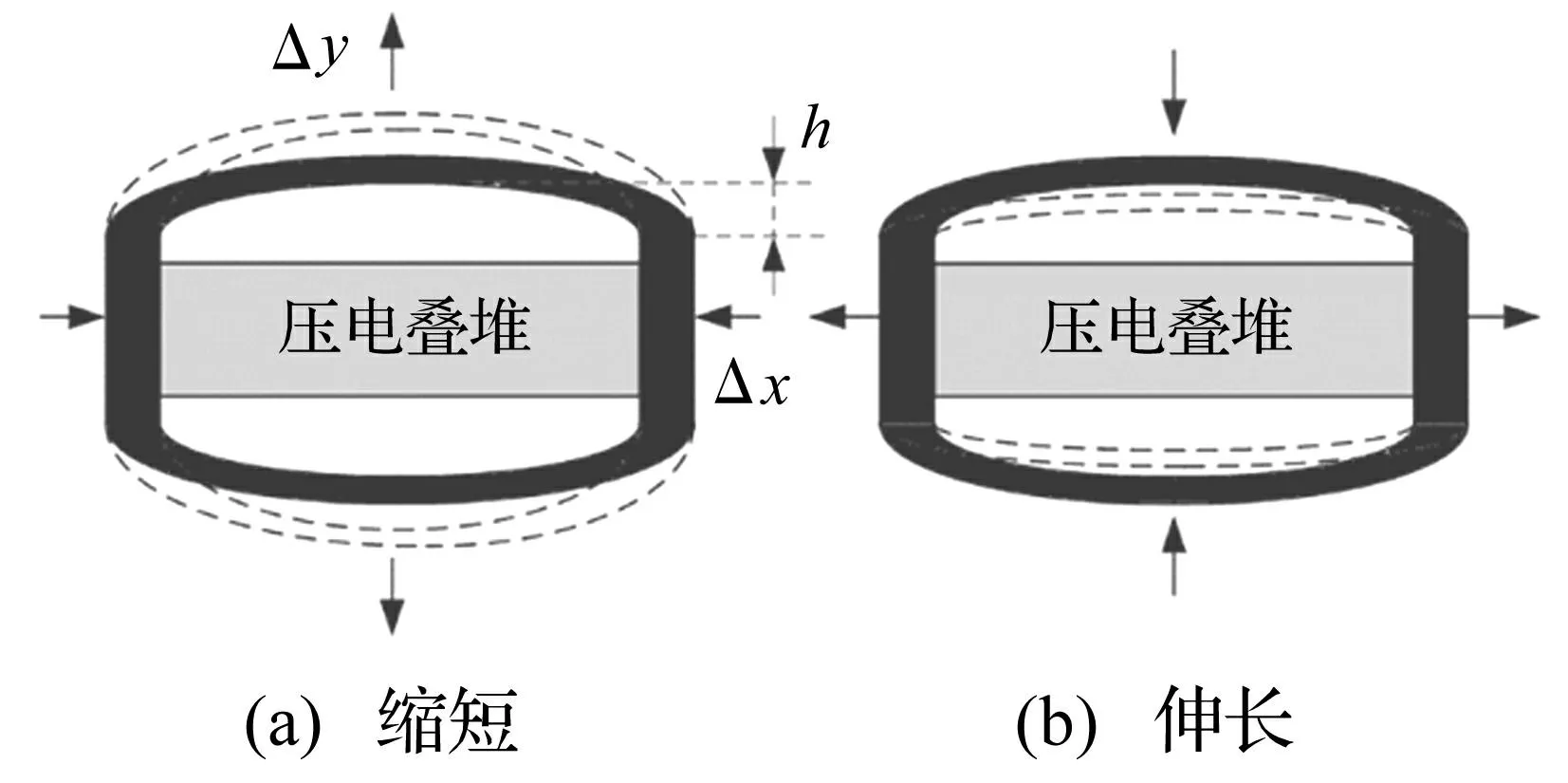
图2　位移放大结构的工作原理图 Fig.2 Schematic illustration of displacement amplifier

1.3压电振子结构参数设计

压电式悬浮振子由绑定装置、压电叠堆和惯性质量三部分结构组成，通过压电叠堆的伸缩将惯性力传递到听骨链。振子尺寸参数的确定需要考虑到人耳本身的生物力学特性，文献[4]中指出，绑定在听骨链上的振子直径d应该小于3 mm，高度h小于2.4 mm。

为了能够定量地衡量加入位移放大结构后压电振子植入效果的改善情况，设计两种振子结构，并分别建立了与人耳耦合的力学模型，振子的绑定位置均为砧骨长突，如图3所示。其中图3(a)中的振子没有加入位移放大结构，直径为2.2 mm，高度为2 mm，总体质量为25 mg。图3(b)中的振子加入了位移放大结构，直径尺寸为2.4 mm，高度为2.3 mm，总体质量为28 mg。

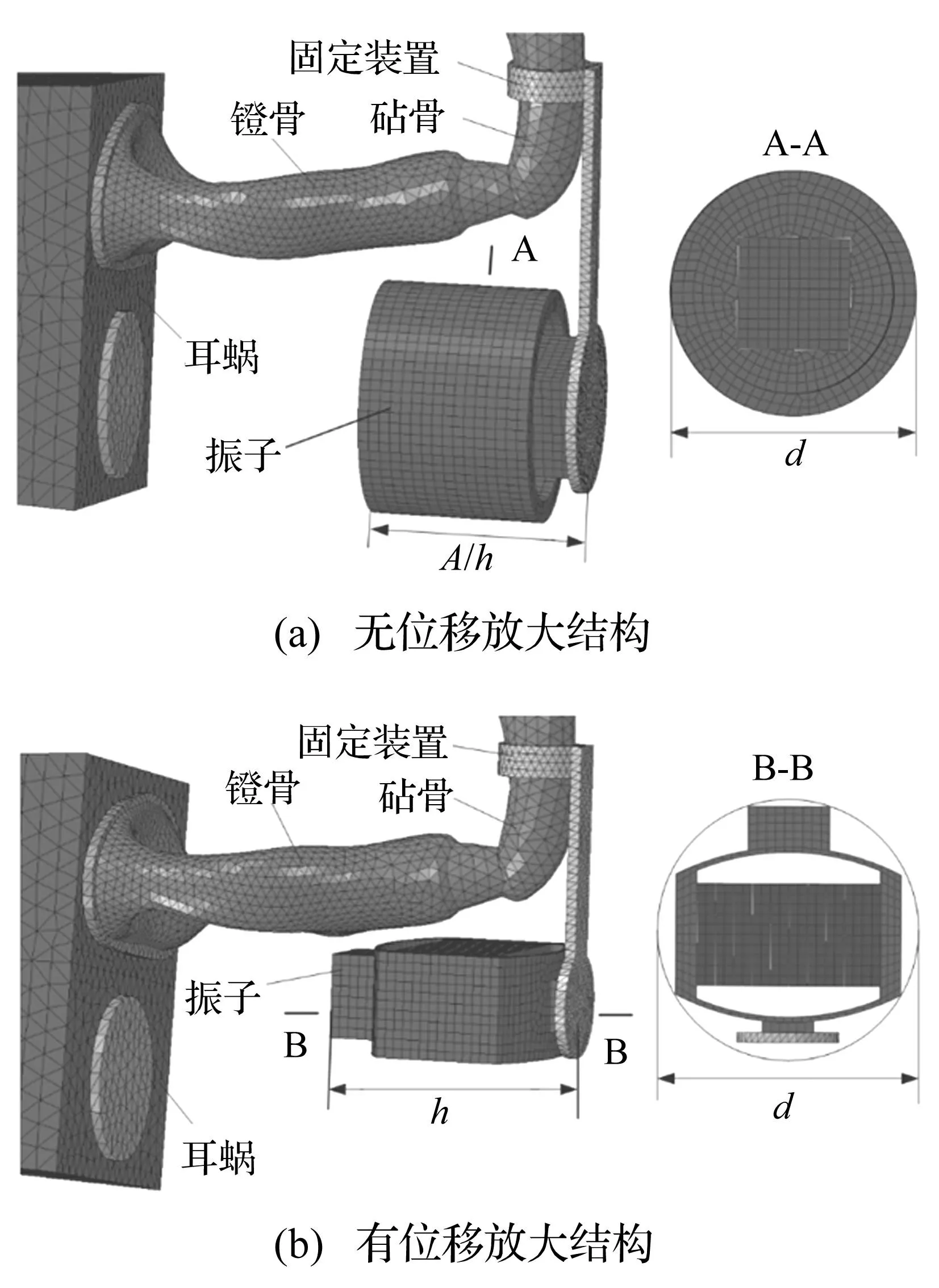
图3　人耳与振子的耦合模型 Fig.3 Coupled model of human ear and actuator

同时，两种压电振子的悬浮质量大小和压电叠堆参数均取为相同，其中，悬浮质量的大小为10 mg，压电叠堆的层数为20，截面尺寸为1 mm×1 mm。本研究中，单层压电陶瓷的材料选为软性的PZT-5H，其作为生物工程材料已被应用于人体的微型驱动器[5]。基于生物相容性的考虑，绑定装置与惯性质量均采用钛合金材料。

2结果与分析

2.1人耳有限元模型的有效性

为了验证模型的有效性，首先模拟正常的人耳声激励，于外耳道的入口处施加90 dB SPL声压，并将计算结果与人耳实验测量数据以及相关的有限元模型仿真结果进行比对，如图4和图5所示。

图4　鼓膜脐部与镫骨底板的位移响应 Fig.4 Displacement response of tympanic membrane umbo and stapes footplate

图4为模型计算的鼓膜脐部与镫骨底板的位移响应，并列出了Gan等的实验测量数据平均值[20]以及有限元模型[16]的计算结果。如图所示，在250~8 000 Hz的频率范围内，本模型与Gan等的模型计算的镫骨底板位移相似度较高，而鼓膜脐部的位移结果则存在一定程度的不同，在250~2 000 Hz和2 000~8 000 Hz的两个频段内分别高于和低于Gan等的计算曲线。同时，通过与实验结果的比较可知，本模型所计算的镫骨底板位移，在低于3000Hz的频率内与实验曲线吻合较好，但在3 000~8 000 Hz的高频处则低于实验测量值，最大可达到8 000 Hz处的-12.38 dB，并且这样的现象也出现在了Gan等的模型计算结果之中。需要指出的是，现阶段的人耳生物力学研究结果表明，人耳特别是中耳的部分结构具有粘弹性的材料特性[21-22]，并用于表征人耳系统的能量耗散机制。本研究以及Gan的有限元模型中，都是通过瑞利阻尼来表达能量耗散，而此种形式所定义的阻尼会随着频率的增大而增大，因此，在一定程度上导致了计算结果与实验数据在高频处的偏差。基于上述的分析，并考虑到个体的差异性，本模型总体上可以用于模拟中耳的传递特性。

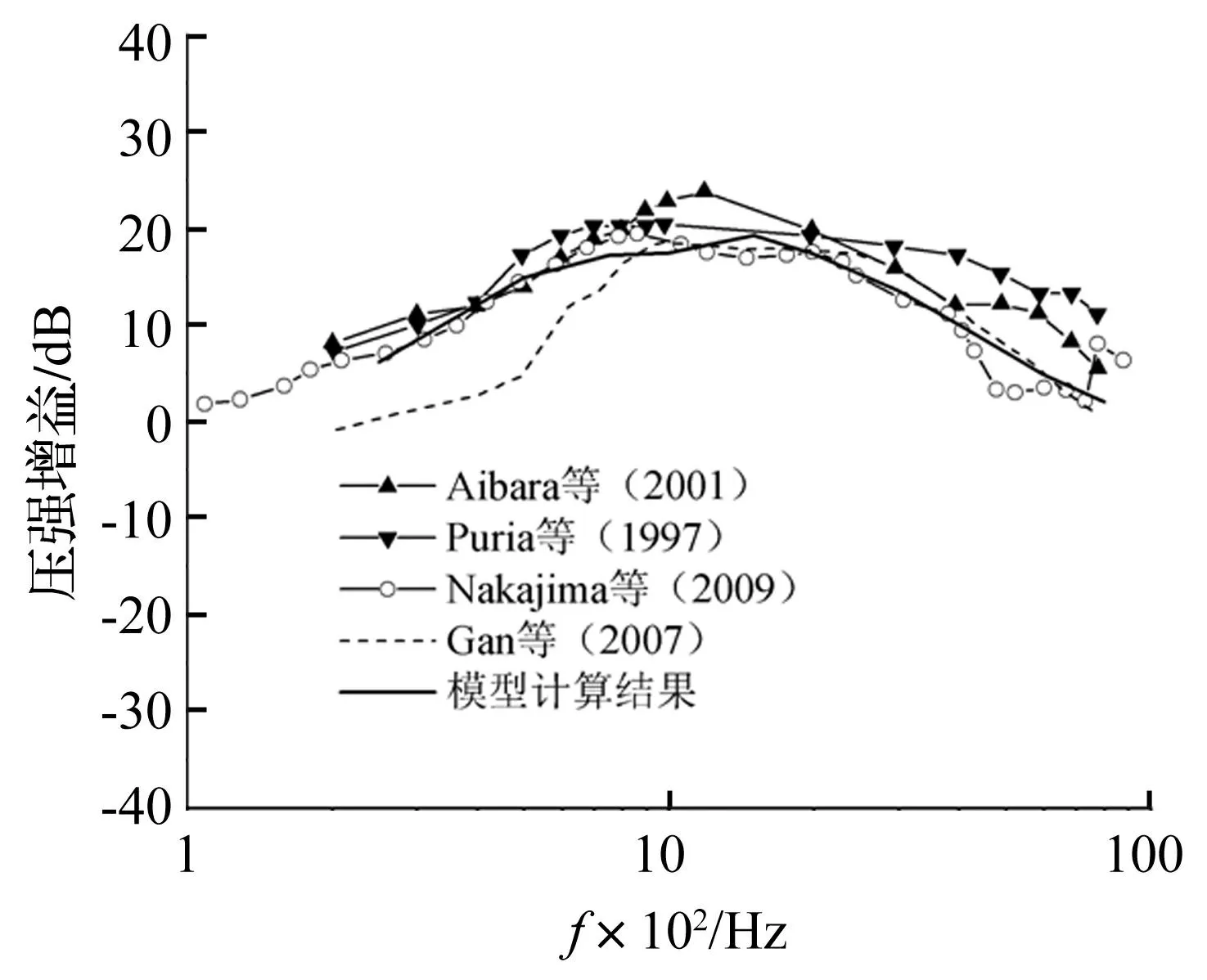
图5　中耳压强增益与实验值对比 Fig.5 Comparison of model-derived middle ear pressure gain with experimental data

中耳压强增益定义为前庭阶靠近卵圆窗处的压强与外耳道内鼓膜附近的压强的比值。图5为模型计算得到的中耳压强增益，并将结果与实验数据[12-13,23]和有限元计算结果[16]进行了比较。由图可见，模型分析得到的中耳压强增益处于一个合理的范围之内，并与Nakajima等[23]的实验数据较为接近，于1 500 Hz处具有20 dB的最大增益值。这说明本文建立的包含耳蜗的人耳有限元模型能够准确地模拟人耳的动力学特性，可以用于人工中耳植入特性的研究。

2.2压电振子的等效声压级

人工中耳植入特性的研究中，一般都以等效声压级作为其植入性能的衡量指标。等效声压级表达了振子驱动电压所对应的外耳道声激励的水平，通过相同的镫骨底板位移响应进行表征，如式(3)所示。

(3)

式中:Peq为等效声压级，dtr和dac分别为振子激励和外耳道声激励下的镫骨底板位移。

为了定量地表达加入位移放大结构前后的植入效果，基于上面建立的两种振子与人耳的耦合力学模型，以90 dB SPL外耳道声激励下的镫骨底板位移作为参考，计算了1 V电压激励下两种不同结构的等效声压级，如图6所示。

图6　两种振子的等效声压级比较 Fig.6 Comparison of equivalent sound pressure between two types of actuators

如图可见，加入了位移放大结构后，压电振子的高频植入效果有了较为明显的改善，1 V电压激励所对应的等效声压级于1 000 Hz处由84 dB增大到86 dB，于4 000 Hz处由103 dB增大到115 dB，随着频率的增加，最大可达到8 000 Hz处的132 dB。由于感音神经性听力损伤多发生于高频段[5]，这将有利于此类患者的听力补偿。同时，该结果也说明，对于相同的等效声压级要求，加入位移放大结构后的压电振子所需的输入电压将会明显的降低。

2.3压电振子的功耗

压电振子的功耗是衡量人工中耳实际适用性的一项重要指标，在有效值为Vrms频率为f的正弦电压的激励下，其对应的电流Irms和功耗Prms分别为：

Irms=2πfCVrms

(4)

式中:C为压电叠堆的电容值，取决于压电叠堆的材料与尺寸，大小为2 893 pF。

本研究中，由于两种振子所采用的压电叠堆参数完全相同，因此，特定的激励频率下，功耗完全取决于激励电压的大小。同时，人工中耳压电振子的设计中，通常都以100 dB SPL 等效声压级所需的激励力、激励位移等作为振子所要满足的基本设计指标[4]，因此，首先由有限元模型计算得到两种压电振子对应于100 dB SPL等效声压级所需的输入电压，再通过式(4)计算得到不同频率下的功耗，结果如图7所示。

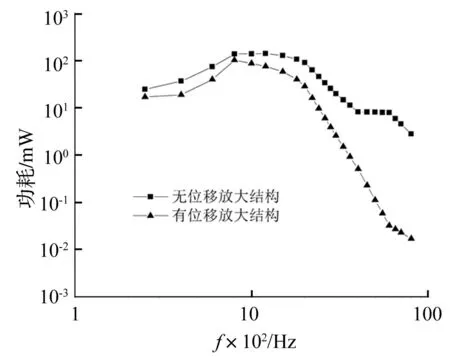
图7　两种振子的功耗比较 Fig.7 Comparison of power consumption between two types of actuators

如图所示，加入了位移放大结构之后，压电振子于250~8 000 Hz频域内的功耗得到了有效的降低。加入放大结构前，振子于1 000 Hz、2 000 Hz和4 000 Hz处的功耗分别为215 μW、141 μW和12 μW，加入放大结构后，对应频率点的功耗分别降低为160 μW、44 μW和0.8 μW，随着频率的增加，功耗的降低量会得到更加可观的效果。

3讨论

本文对于压电振子的优化设计，基于压电叠堆本身所具有的输出力大输出位移小的特点，对其输出位移进行放大。实验表明，对砧骨长突施加8.9×10-5N的激励力便可得到100 dB的等效声压级[24]，可见激励听骨链所需的驱动力非常小。本研究中采用的压电叠堆在1 V电压激励下的最大输出力为 0.721 N，远高于所需的激励力要求，最大输出位移为11.86 nm。为此设计了位移增益量为5的放大结构，由图6和图7的计算结果可知，加入位移放大结构后，压电振子的输出特性有了明显的改善，只需更小的输入电压便可得到100 dB的等效声压级要求，证明了该种方法的有效性。

植入式助听装置的设计，要同时考虑到植入空间限制、振子质量大小和绑定状况等因素。本文设计的两种压电振子满足植入空间的尺寸限制，振子质量分别为25 mg和28 mg。文献[24]中指出，听骨链的附加质量处于20~25 mg的范围内将不会对人耳的动力学特性产生显著影响，因此加入位移放大结构后，振子的质量要稍微高于此范围。同时，建立的振子与人耳的耦合模型中，振子与砧骨通过节点直接耦合的方式进行连接，这在实际的手术中是无法实现的，因此，振子的实际植入效果应该略低于计算结果。本文所设计的压电振子，激励位置为砧骨长突，其他可行的激励位置为砧骨体和镫骨头，可以预见，本文对于压电振子的优化设计将同样适用于这两个激励位置。

4结论

设计了一种位移放大结构用于改善人工中耳压电振子的植入效果。应用微CT扫描技术建立包括外耳道、中耳和简化耳蜗的人耳有限元模型，对位移放大结构和压电振子的尺寸、质量、材料等参数进行优化设计。建立了人耳与压电振子的耦合力学模型，用于压电振子植入效果的评价，并基于该模型计算加入位移放大结构前后压电振子的等效声压级和功耗。结果显示，采用位移放大结构后，压电振子于中高频的等效声压级得到明显的提升，同时功耗也得到了一定程度的降低，达到了优化设计的目的。本文的研究将有利于人工中耳的结构优化和全植入式人工中耳的进一步研究。

参考文献

[1]Horlbeck D. Fully implantable ossicular stimulator [J]. Operative Techniques in Otolaryngology-Head and Neck Surgery, 2010, 21(3): 207-210.

[2]Hong E P, Park I Y, Seong K W, et al. Evaluation of an implantable piezoelectric floating mass transducer for sensorineural hearing loss [J]. Mechatronics, 2009, 19(6): 965-971.

[3]Wang Z, Abel E, Mills R, et al. Assessment of multi-layer piezoelectric actuator technology for middle-ear implants [J]. Mechatronics, 2002, 12(1): 3-17.

[4]Hong E P, Rim M K, Lee S H, et al. Vibration modeling and design of piezoelectric floating mass transducer for implantable middle ear hearing devices[J]. Ieice Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2007, 90(8): 1620-1627.

[5]Wang Z, Mills R, Luo H, et al. A micropower miniature piezoelectric actuator for implantable middle ear hearing device [J]. Biomedical Engineering, IEEE Transactions on, 2011, 58(2): 452-458.

[6]Elhadrouz M, Ben Zineb T, Patoor E. Finite element analysis of a multilayer piezoelectric actuator taking into account the ferroelectric and ferroelastic behaviors [J]. International Journal of Engineering Science, 2006, 44(15): 996-1006.

[7]Handzel O, Wang H, Fiering J, et al. Mastoid cavity dimensions and shape: method of measurement and virtual fitting of implantable devices [J]. Audiology and Neurotology, 2009, 14(5): 308-314.

[8]Niezrecki C, Brei D, Balakrishnan S, et al. Piezoelectric actuation: State of the art [J]. The Shock and vibration digest, 2001, 33(4): 269-280.

[9]Bornitz M, Hardtke H J, Zahnert T. Evaluation of implantable actuators by means of a middle ear simulation model [J]. Hearing Research, 2010, 263(1): 145-151.

[10]Wang X, Hu Y, Wang Z, et al. Finite element analysis of thecoupling between ossicular chain and mass loading for evaluation of implantable hearing device [J]. Hearing Research, 2011, 280(1): 48-57.

[11]Stieger C, Bernhard H, Waeckerlin D, et al. Human temporal bones versus mechanical model to evaluate three middle ear transducers [J]. Journal of Rehabilitation Research and Development, 2007, 44(3): 407.

[12]Puria S, Peake W T, Rosowski J J. Sound-pressure measurements in the cochlear vestibule of human-cadaver ears [J]. The Journal of the Acoustical Society of America, 1997, 101: 2754.

[13]Aibara R, Welsh J T, Puria S, et al. Human middle-ear sound transfer function and cochlear input impedance [J]. Hearing research, 2001, 152(1): 100-109.

[14]Kim N, Homma K, Puria S. Inertial bone conduction: Symmetric and anti-symmetric components [J]. Journal of the Association for Research in Otolaryngology, 2011, 12(3): 261-279.

[15]Steele C, RLim K M. Cochlear model with three-dimensional fluid, inner sulcus and feed-forward mechanism [J]. Audiology and Neurotology, 1999, 4(3-4): 197-203.

[16]Gan R Z, Reeves B P, Wang X. Modeling of sound transmission from ear canal to cochlea [J]. Annals of Biomedical Engineering, 2007, 35(12): 2180-2195.

[17]Gan R Z, Sun Q, Feng B, et al. Acoustic-structural coupled finite element analysis for sound transmission in human ear-Pressure distributions [J]. Medical Engineering & Physics, 2006, 28(5): 395-404.

[18]Wittbrodt M J, Steele C R, Puria S. Developing a physical model of the human cochlea using microfabrication methods [J]. Audiology and Neurotology, 2006, 11(2): 104-112.

[19]Shih W Y, Shih W H, Aksay I A. Scaling analysis for the axial displacement and pressure of flextensional transducers [J]. Journal of the American Ceramic Society, 1997, 80(5): 1073-1078.

[20]Gan R Z, Wood M W, Dormer K J. Human middle ear transfer function measured by double laser interferometry system [J]. Otology & Neurotology, 2004, 25(4): 423-435.

[21]Daphalapurkar N P, Dai C, Gan R Z, et al. Characterization of the linearly viscoelastic behavior of human tympanic membrane by nanoindentation [J]. Journal of the Mechanical Behavior of Biomedical Materials, 2009, 2(1): 82-92.

[22]Zhang X, Gan R Z. Experimental measurement and modeling analysis on mechanical properties of incudostapedial joint [J]. Biomechanics and Modeling in Mechanobiology, 2011, 10(5): 713-726.

[23]Nakajima H H, Dong W, Olson E S, et al. Differential intracochlear sound pressure measurements in normal humantemporal bones [J]. Journal of the Association for Research in Otolaryngology, 2009, 10(1): 23-36.

[24]Ko W H, Zhu W L, Maniglia A J. Engineering principles of mechanical stimulation of the middle ear [J]. Otolaryngologic Clinics of North America, 1995, 28(1): 29.