串列双幅典型断面三分力系数气动干扰效应

第一作者刘志文男，博士，副教授，1975年7月生

邮箱：liuzhiwen757@126.com

串列双幅典型断面三分力系数气动干扰效应

刘志文，陈政清

(湖南大学土木工程学院，长沙410082)

摘要：采用风洞试验与数值模拟相结合的方法对串列双幅典型断面(矩形断面、Π型断面及流线型断面)三分力系数和斯脱罗哈数的气动干扰效应进行了研究。首先针对宽高比为5的单幅矩形断面分别进行了三分力系数的数值模拟和风洞试验测试，数值模拟结果与风洞试验结果吻合良好；然后对串列双幅典型断面不同间距比D/B(D为双幅断面之间净间距，B为单幅断面宽度)对应的三分力系数及斯脱罗哈数进行了数值模拟。研究显示：上游断面阻力系数与单幅断面比较接近，下游断面阻力系数则随间距比D/B的增加而增加；上游断面升力系数、升力矩系数脉动根方差气动干扰因子明显小于下游断面升力系数脉动根方差气动干扰因子，两者均随间距比D/B先增加后减小。

关键词：串列双幅断面；三分力系数；气动干扰效应；数值模拟；风洞试验

基金项目：国家自然科学基金资助项目(50608030, 51178181)；湖南省高校创新平台开放

收稿日期：2012-07-05修改稿收到日期：2013-12-19

中图分类号:U441.3文献标志码：A

Aerodynamic interference effects on aerostatic coefficients of typical sections in tandem arrangement

LIUZhi-wen,CHENZheng-qing(College of Civil Engineering, Hunan University, Changsha 410082, China)

Abstract:Aerodynamic interference effects on aerostatic coefficients and Strouhal numbers of two sections in tandem, namely, two rectangular sections in tandem, two Π-type sections in tandem and two streamlined sections in tandem, were investigated using numerical methods and wind tunnel tests. To validate the accuracy of the numerical methods, the numerical simulation of flow passing a fixed rectangular section with a width-to-depth ratio of 5 was carried out, and the numerical results agreed well with the experimental results. The aerostatic coefficients and Strouhal numbers of different types of two sections in tandom and with a varying separation ratio of D/B(D is the net distance between two sections in tandem, B is the width of the single section) were simulated separately with numerical methods. The results show that the drag coefficients of windward section are close to those of single section, and the drag coefficients of leeward section increase with the increase in D/B; the RMSs of lift and pitching moment coefficients of windward section are significantly less than those of leeward section, and they first increase and then decrease with the increase in D/B.

Key words:two sections in tandem arrangement; aerostatic coefficient; aerodynamic interference effect; numerical simulation; wind tunnel experiment

随着交通量的增加，如何提高桥梁的通行能力越来越受到重视，建设双层桥面桥梁或双幅桥面桥梁是解决这一问题的主要措施之一。在工程实践中，双幅桥面桥梁主要有以下两大类：①桥梁新建时将主梁设计成平行且相互独立分离的两幅桥；②在已建桥梁附近再修建一座与其平行的桥梁。这两类桥由于主梁距离较近，在气流作用下，上游桥面与下游桥面之间存在一定的相互影响，如上、下游桥面气动干扰所引起的双幅桥面主梁涡激共振、颤振稳定性、抖振响应及上下游桥面风荷载等都与单幅主梁断面存在一定的差异，这些影响称为双幅桥面的“气动干扰效应”。随着桥梁跨度的增加，双幅桥面桥梁主梁之间的气动干扰将不容忽视。

气动干扰问题很早就受到关注，而圆柱的气动干扰问题由于其具有广泛的工程应用背景，其研究成果也最多[1-5]。近些年来，随着双幅桥面桥梁建设逐渐增多，大跨度双幅桥面桥梁的气动干扰问题逐渐受到关注。Rowan等[6]针对新塔科马桥，进行了双幅桥面桥梁气动干扰效应研究，通过节段模型和全桥模型试验检验了两座桥的气动干扰效应。Akihiro等[7]对日本大板关西国际机场联络大桥(两公路梁桥之间夹有一与其平行的铁路梁桥)进行了节段模型风洞试验研究；Kimura等[8]研究了串列双幅桥面桥梁之间净间距对双桥面气动干扰效应的影响，研究显示双幅桥面桥梁气动干扰问题十分复杂，当净间距与梁宽之比达到8以上仍存在一定的干扰效应。刘志文等[9-12]对以广州平胜大桥、青岛湾大桥工程红岛航道桥为依托，对大跨度双幅桥面桥梁气动干扰效应进行了试验研究，并对串列双幅典型断面的涡激振动气动干扰效应进行了试验研究。郭震山等[13]以天津海河大桥附近规划建造的一座独塔分离双箱钢箱梁斜拉桥为工程背景，对既有桥梁与新建桥梁主梁之间三分力系数气动干扰效应进行了试验研究。综合以上研究文献可知，大跨度双幅桥面桥梁的气动干扰效应不容忽视，并已引起许多学者的关注，但目前研究重点集中在具体工程，尚缺乏系统研究。对实际桥梁主梁断面进行适当简化，从而对串列双幅典型断面的气动干扰效应进行研究对于研究大跨度双幅桥面桥梁的气动干扰效应具有重要意义。

1典型断面几何参数确定

考虑到实际桥梁断面形式多样，且有栏杆、检修车轨道等附属设施的影响，若直接采用实际桥梁断面进行气动干扰效应的研究，其研究难度较大，且不能抓住气动干扰的主要矛盾，鉴于此，本项目重点针对形状相对比较简单的断面进行气动干扰效应的研究，以尽量获得断面形状、间距等主要设计参数对双幅桥梁断面的气动干扰效应规律。

研究过程中，对实际桥梁主梁断面进行适当简化，设计了三类典型断面(矩形断面、Π型断面和流线型断面)。矩形断面作为典型的钝体断面，在土木工程中有着广泛的应用背景，许多土木工程的典型结构构件是以矩形断面为原形发展起来的，如大跨度桥梁的主梁断面、桥塔断面和桥墩断面等，其气动性能的研究具有重要的意义。Larsen[14]采用离散涡方法对宽高比为5的矩形断面气动性能进行了数值模拟。Matsumoto[15]针对宽高比为5的矩形断面进行了表面压力风洞试验测试，研究显示矩形断面表面压力相关性要比来流紊流相关性大。近几年以来，由国际风工程协会和欧洲流动、湍流及燃烧研究团队共同发起了针对宽高比为5的矩形断面的气动性能研究(A Benchmark on the Aerodynamics of a Rectangular 5：1 Cylinder,BARC)[16]。Π型断面作为另一类钝体断面，由于其在结构受力性能、材料等方面的因素，从经济的角度考虑，在大跨度斜拉桥、悬索桥中应用较多，如荆沙长江公路大桥、杨浦大桥主梁断面等均采用了这种类型的主梁断面。流线型断面由于其良好的气动性能在大跨度桥梁主梁断面中应用十分广泛。

综合以上研究文献，拟定矩形断面、Π型断面及流线型断面结构几何参数如下：模型宽为B=600 mm(流线型断面不计入风嘴的宽度)，高为H=120 mm，具体几何参数见图1。针对这三类典型断面进行三分力系数的气动干扰效应研究，双幅桥面之间间距为：D/B=0.02,0.1,0.2,0.5,1.0,2.0,3.0,5.0,10.0,20.0(D为双幅断面之间净间距；B为单幅断面宽度。)，共30种工况。

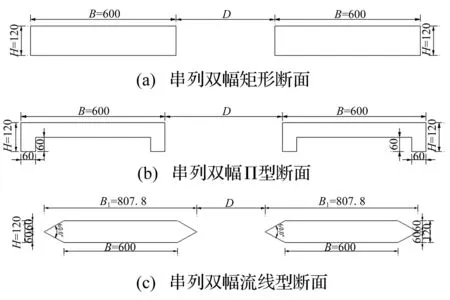
图1　串列双幅典型断面几何参数(单位：mm) Fig.1 Geometrical parameters of typical sections in tandem arrangement (unit: mm)

2单幅断面三分力系数数值模拟

2.1计算区域及网格划分

针对单幅矩形断面，建立如图2(a)所示的计算区域，上游边界距矩形断面上游边为5 B，下游边界距矩形断面下游边为10 B，上、下两侧边界距矩形断面中心均为5 B。计算域边界条件为：矩形断面表面为无滑移壁面边界条件，即VX=0 m/s，VY=0 m/s；上游、上、下侧边界条件为：VX=V0cosa，VX=V0sina，其中α为风攻角，来流风速为V0=10.0 m/s；下游边界条件为压力出口边界，即∂p/∂n=0。空气密度为ρ=1.225 kg/m3，以矩形断面宽度为参考尺寸的雷诺数约为Re=V0B/ν=4.0×105。计算网格采用分块结构化网格，在靠近断面处加密，然后逐步放大，离断面最近的网格间距为0.006B，单元总数为48 400，矩形断面网格如图2(b)所示。单幅Π型断面和单幅流线型断面的计算域和边界条件设置与单幅矩形断面的一致，图2(c)、(d)分别给出了单幅Π型断面和单幅流线型断面网格图。采用基于雷诺平均的k-ωSST湍流模型对流场进行模拟，采用SIMPLE算法求解动量方程中速度分量和压力的耦合问题；采用二阶迎风格式求解速度分量与对流项，时间步长均t=0.005 s。

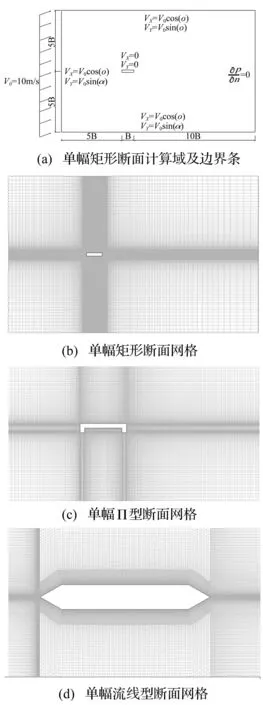
图2　单幅断面计算域与网格 Fig.2 Computational domain and meshes of the single sections

2.2单幅断面三分力系数计算结果

单幅断面的阻力系数、升力系数、升力矩系数及斯托罗哈数定义如下：

(1)

式中：ρ为空气密度；V为来流风速(m/s)；B为单幅断面宽度。

表1给出了单幅断面三分力系数数值模拟结果与试验及已有文献结果。从表1可以看出，单幅矩形断面阻力系数、斯脱罗哈数(St)的数值模拟结果与风洞试验测试结果吻合较好；而且由于矩形断面在0°风攻角风作用下，其升力系数与升力矩系数应为0，本文数值模拟结果均比试验值小，更接近真实值。表明本文数值模拟结果具有足够的精度。

考虑到影响几何断面三分力系数计算结果的主要因素是计算区域、计算网格、湍流模型以及边界条件等，对于单幅断面和双幅断面而言，从断面流场计算的角度考虑，两者之间本质上是没有差别的，故在验证了单幅断面计算精度的前提下，是可以采用本文的数值模拟方法进行不同间距条件下的串列双幅断面三分力系数气动干扰效应研究是可行的。

3串列双幅断面三分力系数气动干扰效应

3.1计算区域及网格划分

采用计算流体力学软件FLUENT分别对串列矩形断面、串列Π型断面和串列流线型断面进行了不同间距比D/B条件下的三分力系数数值模拟。建立如图3(a)所示的计算区域及计算边界条件，即计算区域上游边界距上游矩形断面迎风侧为5 B，计算区域下游侧距上游矩形断面背风侧为20 B，计算区域的上、 下侧边界距断

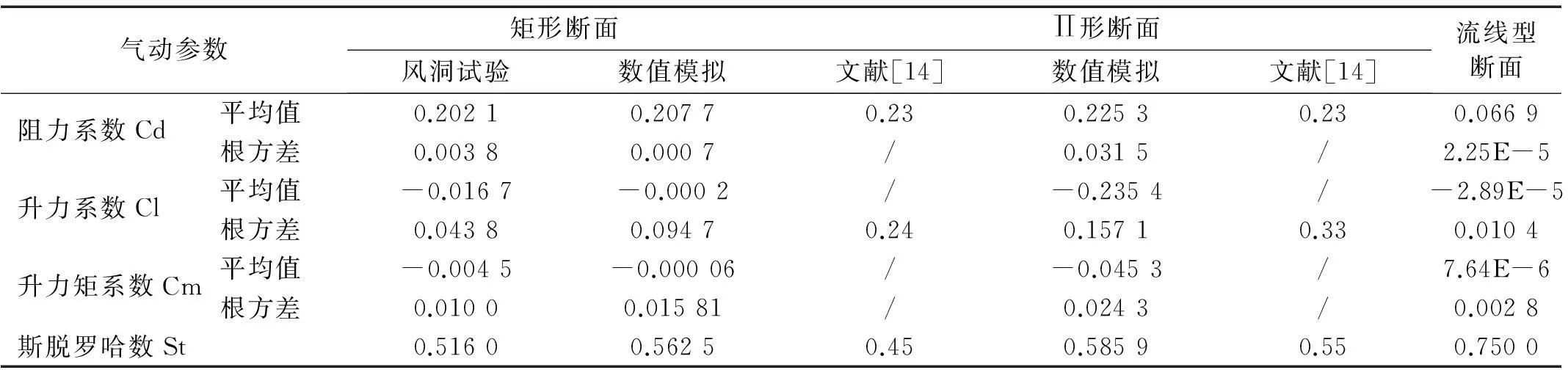
表1　单幅断面三分力系数及St数数值模拟与试验结果

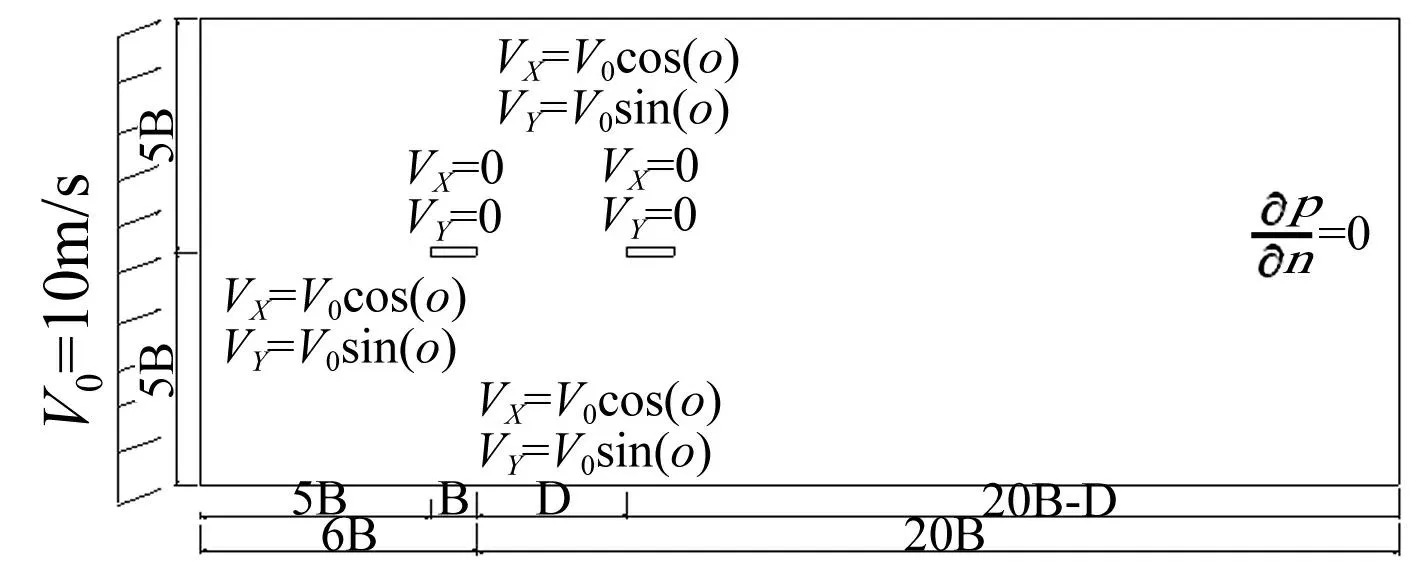
图3　串列双幅矩形断面计算区域及边界条件 Fig.3 Computational domain and boundary conditions of two rectangular sections in tandem arrangement

图4　间距比D/B=0.5、1时串列双幅矩形断面网格 Fig.4 Meshes of two rectangular sections in tandem arrangement with D/B=0.5 and 1

图5　间距比D/B=0.5、1时串列双Π型断面网格 Fig.5 Meshes of two Π-typed sections in tandem arrangement with D/B=0.5 and 1

图6　间距比D/B=0.5、1时串列双流线型断面网格 Fig.6 Meshes of two streamlined sections in tandem arrangement with D/B=0.5 and 1

面中心为5 B。计算域边界条件设置与单幅断面相同，此不赘述。限于篇幅，图4~6仅给出串列双幅矩形断面、双幅Π型断面及双幅流线型断面间距比为D/B=0.5、1.0对应的网格。

3.2串列双幅断面三分力系数计算结果

图7~图9所示为间距比为D/B=1.0和2.0时串列双幅矩形断面、Π型断面及流线型断面上、下游断面系数三分力系数时程曲线，其中CD1,CL1,Cm1分别为上游断面的阻力系数、升力系数和升力矩系数，CD2,CL2,Cm2分别为下游断面的阻力系数、升力系数和升力矩系数。从图7、8中可以看出，当间距比D/B=1.0及2.0时，上游钝体断面(矩形断面、π型断面)的阻力系数大于下游断面的阻力系数，下游钝体断面升力系数根方差及升力矩系数根方差大于上游断面的升力系数及升力矩系数根方差。从图9中可以看出，当间距比D/B=1.0时，上游流线型断面阻力系数小于下游流线型断面阻力系数，下游流线型断面升力系数及升力矩系数根方差大于上游流线型断面升力系数及升力矩系数根方差；当间距比D/B=2.0时，上游流线型断面阻力系数与下游流线型断面阻力系数接近，下游流线型断面升力系数及升力矩系数根方差大于上游流线型断面升力系数及升力矩系数根方差。

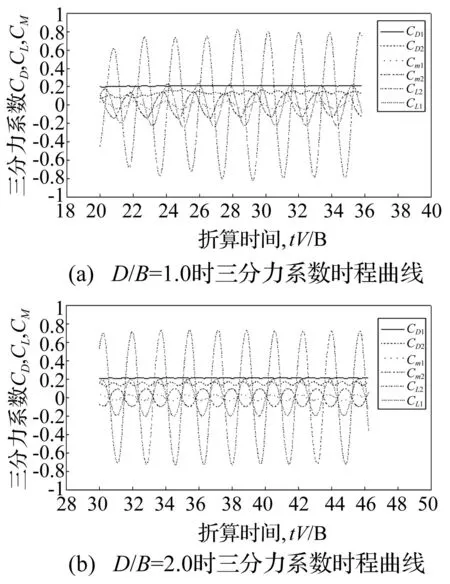
图7　串列双幅矩形断面三分力系数时程 Fig.7 Time histories of aerostatic coefficients of two rectangular sections in tandem arrangement

图8　串列双幅Π型断面三分力系数时程 Fig.8 Time histories of aerostatic coefficients of two Π-typed sections in tandem arrangement

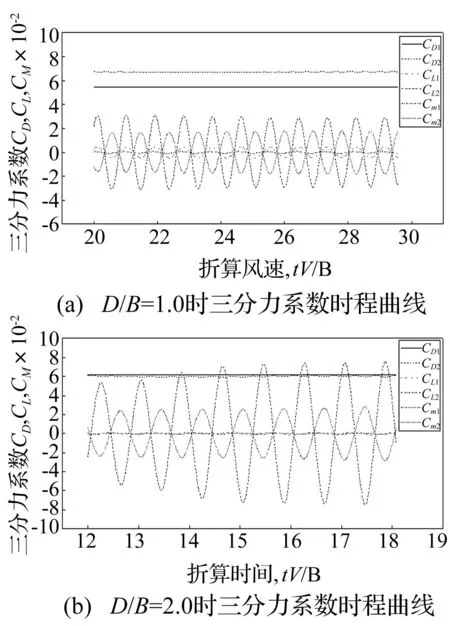
图9　串列双幅流线型断面三分力系数时程 Fig.9 Time histories of aerostatic coefficients of two streamlined sections in tandem arrangement

图10　串列双幅矩形断面三分力系数随间距比D/B变化 Fig.10 Aerostatic coefficients of two rectangular sections in tandem arrangement with D/B

图10~12所示为串列双幅矩形断面、双幅Π型断面及双幅流线型断面三分力系数随间距比D/B的变化曲线。从图10、11中可以看出，上游矩形断面阻力系数平均值与单幅断面比较接近，而下游矩形断面阻力系数平均值随间距比D/B的增加而增加，当间距比D/B=20时，下游矩形断面的阻力系数平均值仍小于上游矩形断面的阻力系数；下游矩形断面升力系数、升力矩系数根方差随间距比D/B的增大而先增加后减小，且大于上游矩形断面的升力系数、升力矩系数根方差。从图11中看出，串列双幅Π型断面三分力系数随间距比D/B的变化规律与串列双幅矩形断面三分力系数随间距比D/B的变化规律相似。从图12中可以看出，上、下游流线型断面阻力系数随间距比D/B的增加而先增加后减小；当间距比D/B≤3.0时，上游流线型断面阻力系数小于下游流线型断面阻力系数；当间距比D/B>3.0时，上游流线型断面阻力系数大于下游流线型断面阻力系数，且均小于单幅流线型断面阻力系数。下游流线型断面升力系数、升力矩系数根方差随间距比D/B的增大而先增加后减小，且大于上游流线型断面的升力系数、升力矩系数根方差。

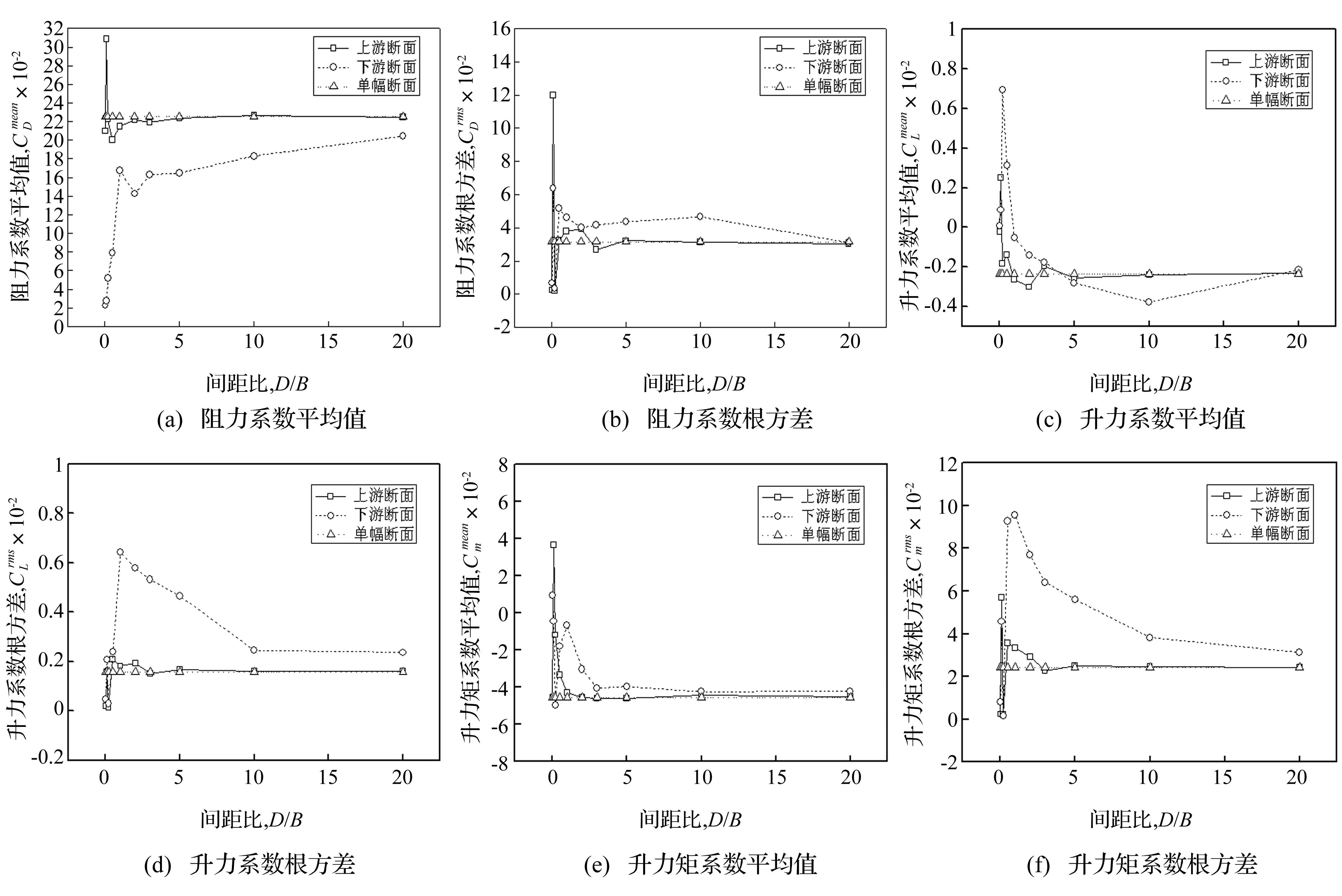
图11　串列双幅Π型断面三分力系数随间距比D/B变化 Fig.11 Aerostatic coefficients of two Π-typed sections in tandem arrangement with D/B

3.3串列双幅断面三分力系数气动干扰因子

为了研究串列双幅典型断面三分力系数及斯脱罗哈数的气动干扰效应，定义如下气动干扰因子：

(2)

式中：IFwindward为上游断面三分力系数或斯脱罗哈数的干扰因子；Cwindward上游断面三分力系数或斯脱罗哈数；IFwindward为下游断面三分力系数或斯脱罗哈数的干扰因子；Cleeward下游断面三分力系数或斯脱罗哈数;Csingle为单幅断面三分力系数或斯脱罗哈数。

图13分别给出了不同断面三分力系数及斯脱罗哈数St气动干扰因子随间距比D/B的变化曲线。从图13中可知：①上游钝体断面(矩形断面、П型断面)，当0.02≤D/B≤1.0时，阻力系数气动干扰因子IFCD=0.9左右；当D/B≥2.0时，气动干扰因子IFCD接近1.0；上游流线型断面，当0.02≤D/B≤3.0时，阻力系数气动干扰因子IFCD=0.51~0.90；当D/B>3.0时，气动干扰因子IFCD=0.82。下游钝体断面阻力系数则随间距比D/B的增加而增加；下游流线型断面，当0.02≤D/B≤3.0时，阻力系数气动干扰因子IFCD=0.70~1.1；当D/B>3.0时，气动干扰因子IFCD=0.75。②上游断面(矩形断面、П型断面、流线型断面)升力系数根方差、升力矩系数根方差气动干扰因子明显小于下游断面升力系数根方差气动干扰因子，两者均随间距比D/B先增加后减小。

图12　串列双幅流线型断面三分力系数随间距比D/B变化 Fig.12 Aerostatic coefficients of two streamlined sections in tandem arrangement with D/B

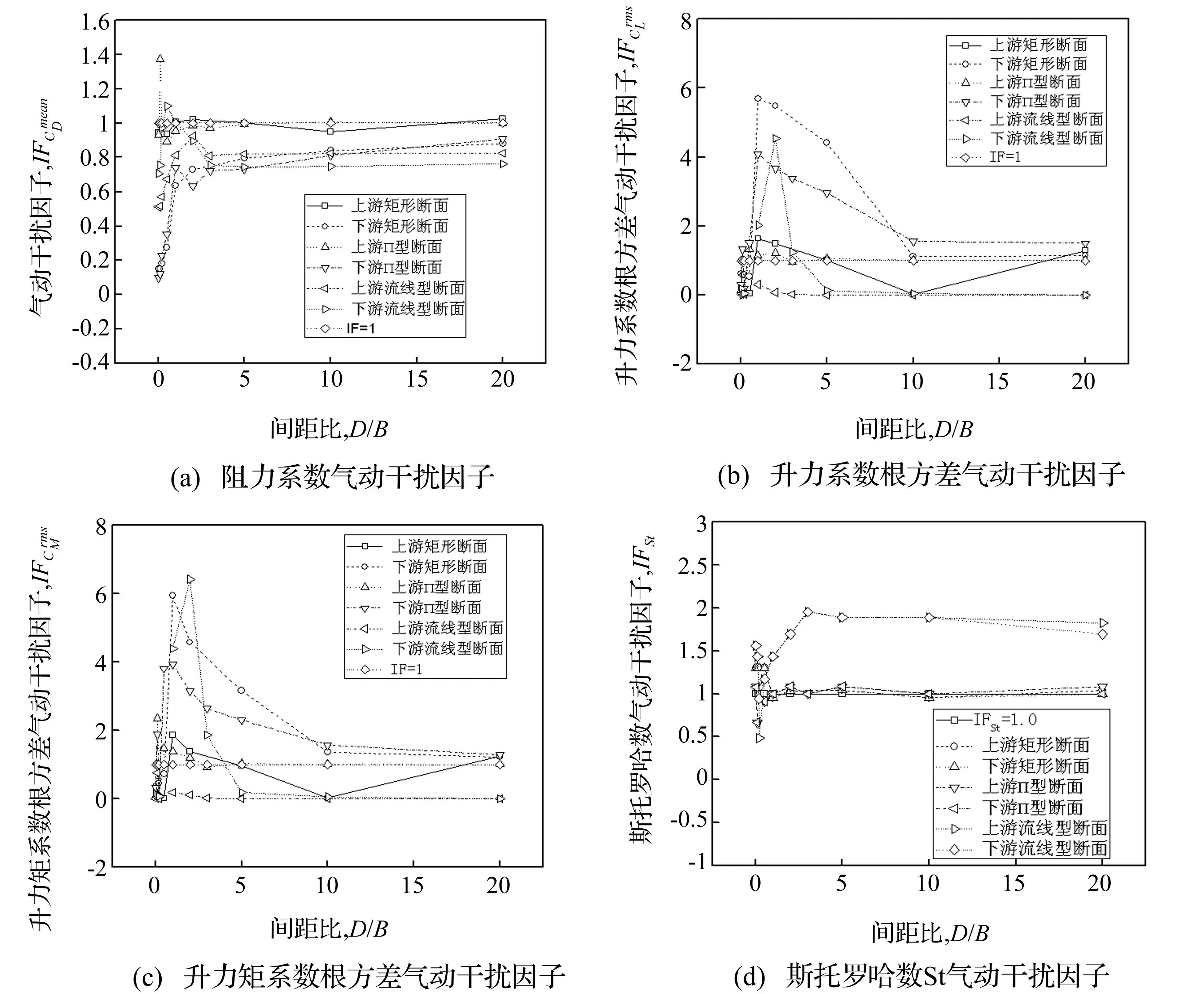
图13　三类典型串列双幅断面三分力系数及斯托罗哈数St气动干扰因子随间距比D/B变化 Fig.13 Aerodynamic interference factors of aerostatic coefficients and Strouhal number of the typical sections in tandem arrangement with D/B

4结论

通过对串列双幅典型断面三分力系数及斯脱罗哈数气动干扰效应研究，得到如下主要结论：

(1)单幅矩形断面三分力系数数值模拟结果与风洞试验测试值吻合较好，表明采用数值模拟方法进行不同间距条件下的串列双幅断面三分力系数气动干扰效应研究是可行的；

(2)上游钝体断面(矩形断面、П型断面)，当0.02≤D/B≤1.0时，阻力系数气动干扰因子IFCD=0.9左右；当D/B≥2.0时，气动干扰因子IFCD接近1.0；下游钝体断面阻力系数则随间距比D/B的增加而增加；

(3)上游流线型断面，当0.02≤D/B≤3.0时，阻力系数气动干扰因子IFCD=0.51~0.90；当D/B>3.0时，气动干扰因子IFCD=0.82。下游流线型断面，当0.02≤D/B≤3.0时，阻力系数气动干扰因子IFCD=0.70~1.1；当D/B>3.0时，气动干扰因子IFCD=0.75。

(4)上游断面(矩形、П型及流线型断面)升力系数根方差、升力矩系数根方差气动干扰因子明显小于下游断面升力系数脉动根方差气动干扰因子，两者均随间距比D/B的增加而先增加后减小。

参考文献

[1]Zdravkovich M M. Review of flow interference between two cylinders in various arrangement[J]. Journal of Fluids Engineering, 1977, 99: 618-633.

[2]Matsumoto M, Shiraishi N, Shirato H. Aerodynamic instabilities of twin circular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 33: 91-100.

[3]Alam M. M., Zhou Y. Strouhal numbers, forces and flow structures around two tandem cylinders of different diameters[J]. Journal of Fluids and Structures, 2008, 24: 505-526.

[4]LIU Xian-zhi, Marc L. Nikitopoulos dimitris. wind tunnel tests for mean drag and lift coefficients on multiple circular cylinders arranged in-line[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 831-839.

[5]Sumner D, Richards M D, Akosile O O. Strouhal number data for two staggered circular cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 859-871.

[6]Rowan A I, Stoyan S, Xie J M, et al. Tacoma narrows 50 years later wind engineering investigations for parallel bridges[J]. Bridge Structures: Assessment, Design and construction, 2005, 1(1): 3-17.

[7]Akihiro H, Naruhito S, Masaru M, et al., Aerodynamic stability of kansai international airport access bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1-3): 533-542.

[8]Kimura K, Shima K, Sano K, et al. Effects of separation distance on wind-induced response of parallel box girders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 954-962.

[9]刘志文,陈政清,刘高,等. 双幅桥面桥梁三分力系数气动干扰效应试验研究[J]. 湖南大学学报(自然科学版), 2008, 35(1): 16-20.

LIU Zhi-wen, CHEN Zheng-qing, LIU Gao, et al.Experimental study of aerodynamic interference effects on aerostatic coefficients of twin decks bridges[J]. Journal of Hunan University (Natural science edition), 2008, 35(1): 16-20.

[10]刘志文, 陈政清. 胡建华,等. 大跨度双幅桥面桥梁气动干扰效应[J]. 长安大学学报(自然科学版), 2008, 28(6): 55-59.

LIU Zhi-wen, CHEN Zheng-qing, HU Jian-hua, et al. Aerodynamic interference effects of large span bridge with twin decks[J]. Journal of Chang’an University (Natural science edition), 2008, 28(6): 55-59.

[11]刘志文, 栗小祜, 陈政清. 均匀流场串列双矩形断面涡激振动气动干扰试验研究[J]. 中国公路学报，2010,23(5): 44-50.

LIU Zhi-wen, LI Xiao-hu, CHEN Zheng-qing. Experiment of Aerodynamic interference on vortex-induced vibration of two rectangular cylinders in tandem in smooth flow field[J].China Journal of Highway and Transport, 2010, 23(5): 44-50.

[12]刘志文，陈政清，栗小祜,等. 串列双流线型断面涡激振动气动干扰试验[J]. 中国公路学报，2010，24(3):51-57.

LIU Zhi-wen, CHEN Zheng-qing, LI Xiao-hu, et al. Aerodynamic interference test on vortex-induced vibration of two streamline cylinders in tandem[J].China Journal of Highway and Transport, 2010, 24(3): 51-57.

[13]郭震山，孟晓亮，周奇,等. 既有桥梁对临近新建桥梁三分力系数气动干扰效应[J]. 工程力学，2010， 27(9): 181-186.

GUO Zhen-shan, MENG Xiao-liang, ZHOU qi, et al. Aerodynamic interference effects of an existed bridge on aerodynamic coefficients of an adjacent new bridge[J]. Engineering Mechanics, 2010, 27(9): 181-186.

[14]Larsen A. Advances in aeroelastic analyses of suspension and cable-stayed bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 73-90.

[15]Matsumoto M, Shirato H, Araki K, et al. Spanwise coherence characteristics of surface pressure field on 2-D bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 155-163.

[16]Schewe G. Reynolds-number-effects in flow around a rectangular cylinder with aspect ratio 1:5[C]//Borri C., Augusti G., Bartoli G. Proceedings of Fifth European and African Conference on Wind Engineering, Florence: Firenze University Press, 2009.