履带急救车非线性减振系统动态性能优化

第一作者杨猛男，博士生，1989年2月生

通信作者徐新喜男，博士，研究员，博士生导师，1965年生

履带急救车非线性减振系统动态性能优化

杨猛，徐新喜，段德光，苏卫华，苏琛

(军事医学科学院卫生装备研究所，天津300161)

摘要：针对履带急救车非线性减振系统在随机激励下的动态性能优化问题，首先提出了一种基于改进的分块增维精细积分法和NSGA-Ⅱ算法的多目标参数辨识方法，对履带急救车非线性减振系统进行了参数辨识；然后，应用Sobol’法分析了减振系统各物理参数对系统输出的全局灵敏度；最后，应用遗传算法对减振系统进行了动态性能优化。结果表明：经过优化，担架台垂向振动加权加速度均方根值由原来的0.521 0 m/s2下降为0.418 3 m/s2，降幅达19.7%，减振系统动态性能得到了明显改善。

关键词：参数辨识；改进的分块增维精细积分法；NSGA-Ⅱ算法；Sobol’法；动态性能优化

收稿日期：2014-08-21修改稿收到日期：2014-10-17

中图分类号:U463.33文献标志码：A

Dynamic performance optimization of a tracked ambulance nonlinear vibration-reduction system

YANGMeng,XUXin-xi,DUANDe-guang,SUWei-hua,SUChen(Institute of Medical Equipment, Academy of Military Medical Sciences, Tianjin 300161, China)

Abstract:For the dynamic performance optimization of a tracked ambulance nonlinear vibration-reduction system under random excitation, a new multi-objective parameter identification method based on the improved partitioning and dimensional increment precise integration method and NSGA-Ⅱ method was proposed to identify the parameters of the tracked ambulance nonlinear vibration-reduction system. The Sobol’ method was used to study the global sensitivity of the parameters with respect to the system output. And then, the dynamic performance was optimized by using genetic algorithm. The optimization results showed that the root mean square value of the stretcher base’s weighted vertical acceleration reduces from 0.5210m/s2 to 0.4183m/s2 with a 19.7% drop, the dynamic performance of the vibration-reduction system is improved significantly.

Key words:parameter identification; improved partitioning and dimensional increment precise integration method; NSGA-Ⅱmethod; Sobol’ method; dynamic performance optimization

加装车载非线性减振系统是提高车内乘员乘坐(卧)舒适性的主要途径，在工程实际中具有广泛的应用，尤其是在一些对振动环境具有特殊要求的车辆上应用更加广泛，例如急救车，其良好的减振性能可以避免伤病员在转运途中受到二次伤害。因此，对车载非线性减振系统进行动态性能优化具有重要的实际意义。

根据试验数据辨识非线性减振系统的物理参数是预测减振系统输出响应的重要手段；对非线性减振系统各物理参数进行灵敏度分析是获得系统参数对输出响应影响程度的主要方法。两者均是非线性减振系统动态性能优化的重要方法和基础。目前，国内外关于参数辨识和灵敏度分析的研究已经很多，方法也较为多样化。在参数辨识方面，Ghanem等[1]提出了一种基于小波分析的参数辨识方法，Pacheco等[2]运用正交函数解决了非线性系统的辨识问题。在灵敏度分析方面，研究方法主要包括多元回归法[3]、Morris法[4]、Sobol’法[5]等。相比于参数辨识，灵敏度分析方法已经发展的较为完备，无论是局部灵敏度分析，还是定性、定量的全局灵敏度分析都有成熟的方法可供参考。但在参数辨识方面，目前却没有发展出一种可供不同工程领域参考的成熟方法，具体问题还需具体分析。

针对目前参数辨识和灵敏度分析的研究现状，首先提出了一种多目标参数辨识方法，并应用该方法，以担架台垂向振动加速度功率谱密度和概率分布为评价指标，以底盘纵梁振动信号为输入，对履带急救车非线性减振系统进行了参数辨识。然后，应用Sobol’法分析减振系统各物理参数对于担架台垂向振动加权加速度均方根值的全局灵敏度。最后，应用遗传算法对减振系统进行了动态性能优化。

1多目标参数辨识方法

多目标参数辨识方法由改进的分块增维精细积分法和NSGA-Ⅱ算法组成，下面分别介绍两种方法。

1.1改进的分块增维精细积分法

将非线性系统运动微分方程表示为

(1)

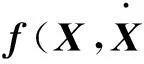
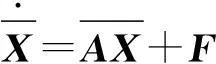
(2)

(3)

记时间步长为τ。令Δt=τ/m，其中m=2L，L= 20。经过推导可得如下计算过程

(4)

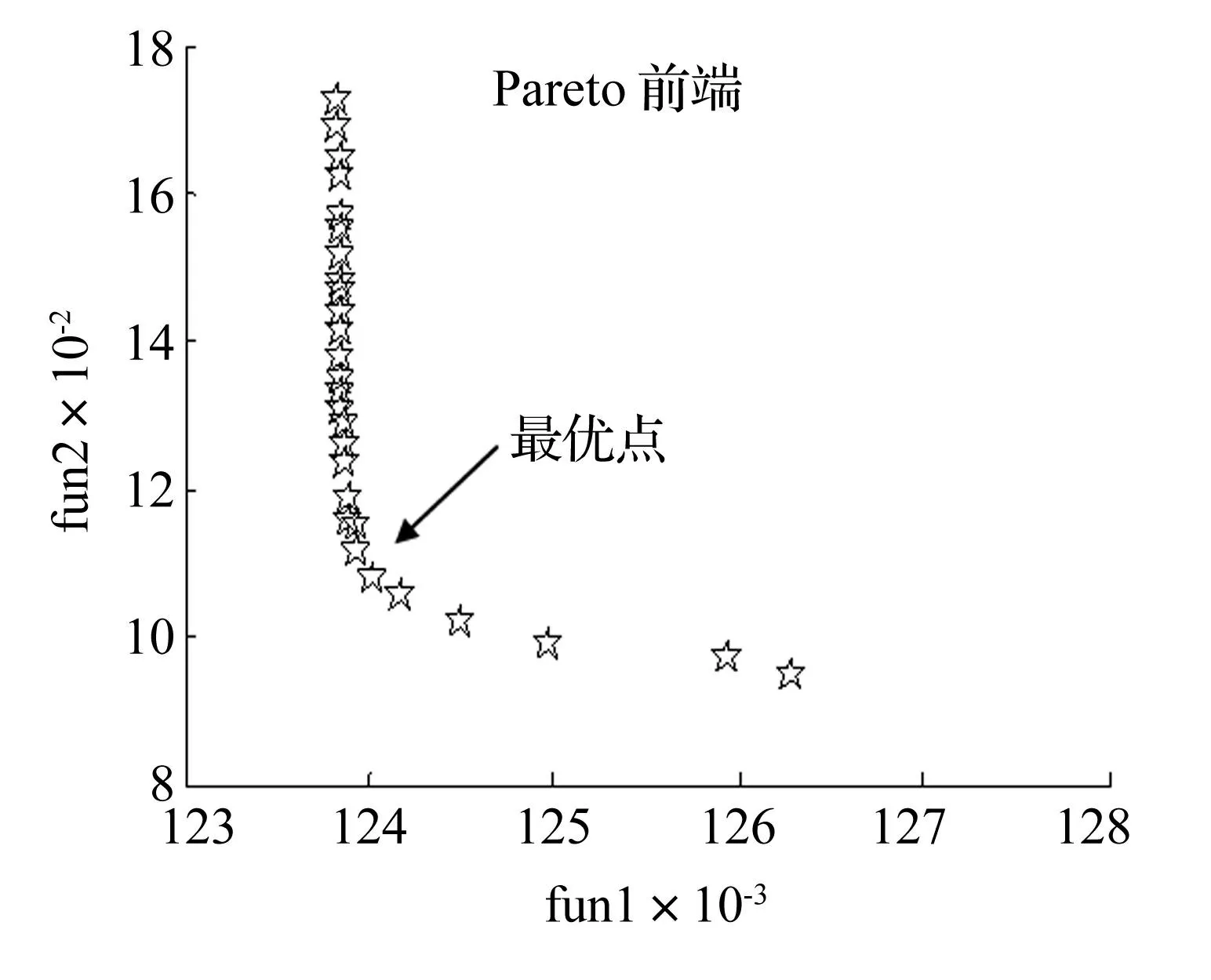
for(iter=0;iter

(5)

当循环(5)结束后，可得

(6)

Y(kτ)=Tk-1Y[(k-1)τ](k=1,2,…)

(7)

式(3)、式(4)、式(5)、式(6)和式(7)构成了分块增维精细积分法。通过观察矩阵F和矩阵H的结构可以发现，算法的计算效率可以继续提高。首先，对矩阵B和矩阵F进行如下分块：

(8)

(9)

通过以上变换，可以使得在每次更新矩阵G时，计算量由原来的2n×2n次乘法变为2n×n次乘法，大大简化了计算。其次，考虑增维后H的特点，Y的最后一行实际上不会对所求结果产生影响，则式(7)可变成如下形式

(10)

即

(11)

式(10)与式(7)相比降低了矩阵维数，这也可以在一定程度上减小计算量。经过式(8)、式(9)、式(10)和式(11)优化后的分块增维精细积分法与原算法相比，矩阵维数和计算量均显著变小，这对于大型结构优化以及长时间仿真具有重要意义。

1.2NSGA-Ⅱ算法

用单一目标或准则对减振系统进行参数辨识所得结果的说服力是不够的，因此有必要对减振系统进行多目标参数辨识。目前，在众多的多目标优化算法中，NSGA-Ⅱ算法无疑是应用最为成功的一个[7-8]。NSGA-Ⅱ算法具有计算量小、搜索效率高的特点，在保持种群多样性和防止优秀个体流失方面表现突出，而且不需要设定初值。所以,选择NSGA-Ⅱ算法作为参数辨识的寻优算法。

1.3多目标参数辨识方法基本流程

(1)建立目标函数。选取多个减振系统输出响应的特征参数为评价指标，应用改进的分块增维精细积分法计算随机激励条件下评价指标的值，并与试验获得的评价指标的值相减，以其差值的平方和为目标函数；

(2)参数设定。根据减振系统实际情况，给出已知参数的值和待辨识参数的范围及约束条件，并对NSGA-Ⅱ算法进行相应设定；

(3)寻优计算。根据已完成的参数设定，应用NSGA-Ⅱ算法对目标函数进行多次寻优计算，直至输出结果稳定，获得最终的Pareto解集；

(4)选择结果。结合工程实际，在Pareto解集中选取合适的点为最优点，以其对应的参数为最终辨识结果。

2减振系统参数辨识

2.1减振系统物理模型

图1　急救车非线性减振系统1/2模型 Fig.1 The 1/2 model of the ambulance nonlinear vibration-reduction system

以文献[9]中的某履带急救车非线性减振系统为研究对象，建立其1/2模型，如图1所示。图中，M1,M2为担架台和大板车厢的质量；J1,J2为担架台和大板车厢的质量在几何中心处绕z轴的转动惯量；Ks,Kz,C1为零刚度减振器的线性刚度、三次非线性刚度和阻尼；K2,C2为橡胶阻尼减振器的刚度和阻尼；l1,l2为担架台和大板车厢的几何中心距离各自减振器沿y轴的距离；q1,q2为振动输入。

Ks、Kz、C1、K2和C2为待辨识参数,M1、M2、J1、J2、l1和l2为已知参数，取值如下：M1=180 kg、M2=2 000 kg、J1=58 kg·m2、J2=3 665 kg·m2、l1= 0.8 m、l2=1.539 m。应用Lagrange方程法推导减振系统运动微分方程，写成式(2)形式如下

式中:Aij(i=5,…,8;j=1,…,8)和Ri(i=1,…,4)的具体表达式见附录1。

2.2参数辨识结果

在参数辨识之前，需要对算法进行一些设置，具体如下：

(1)根据减振系统实际情况给出待辨识参数的取值范围：Ks-[1 000,650 000]、Kz-[1 000,1 000 000]、C1-[500,65 000]、K2-[20 000,8 500 000]、C2-[500,95 000]。

(2)选取文献[10]中履带急救车在越野路(18 km/h)条件下底盘纵梁的振动数据为激励数据，时间长度为80 s，采样频率为250 Hz。

(3)由于担架台振动对伤病员影响较大，而且随机信号的很多时频域指标可以通过其功率谱密度和概率分布推导获得，所以本文选择担架台垂向振动加速度功率谱密度和概率分布为评价指标，建立目标函数如下

(12)

式中:Pxx1和hx1为试验数据的功率谱密度和概率分布；Pxx和hx为仿真数据的功率谱密度和概率分布；p为离散数据个数。

(4)由减振系统实际情况可知，橡胶阻尼减振器的刚度和阻尼大于零刚度减振器的刚度和阻尼，且零刚度减振器的线性刚度大于三次非线性刚度，所以对算法施加的约束条件如下

{Ks

(13)

(5)对NSGA-Ⅱ算法进行如下设置：最优前端个体系数为0.3；种群大小为100；最大进化代数为300；停止代数为200；适应度函数值偏差为1×10-6。

经过以上设置之后，对履带急救车非线性减振系统进行参数辨识，第一前端个体分布如图2所示，其Pareto解集见附录2。

图2　第一前端个体分布图 Fig.2 The first front individual distribution

为了尽可能使两个目标函数值都达到最优，选择图2中所示的点为最优点，其对应的参数辨识结果为Ks=217 435.8 N/m、Kz=30 932.1 N/m、C1= 27 591.2 N·s/m、K2=1457 010.4 N/m、C2= 34 758.2 N·s/m、fun1=0.124 2、fun2=0.105 2。将上述参数重新带入模型，求得仿真条件下担架台垂向振动加速度的功率谱密度和概率分布，并与试验结果进行对比，如图3和图4所示。

图3　功率谱密度对比 Fig.3 The comparison of power spectral density

图4　概率分布对比 Fig.4 The comparison of probability distribution

观察图3和图4可以发现，试验结果与仿真结果基本吻合，尤其是在概率分布方面，吻合程度较高。在功率谱密度方面，试验结果与仿真结果在13~30 Hz和65~75 Hz频率范围内有一定的误差，但由于这两个频率范围内功率谱密度值较小，其差值对结果影响也较小。综合以上分析，辨识结果很好地再现了减振系统对底盘纵梁随机激励的响应，满足使用要求。同时，也证明了本文提出的多目标参数辨识方法的有效性。

3减振系统参数灵敏度分析

参数灵敏度分析包括局部灵敏度分析和全局灵敏度分析两种。针对本文的减振系统，由于零刚度减振器表现出较强的非线性，且各个参数之间相差一个或多个数量级，不宜采用局部灵敏度分析。所以，本文采用Sobol’法对减振系统进行全局灵敏度分析，研究减振系统各参数对于担架台垂向振动加权加速度均方根值的灵敏度。其中，加权加速度均方根值的计算公式如下

(14)

式中:f为频率；Sz(f)为担架台垂向振动加速度功率谱密度；ω(f)为频率加权函数，对于垂向，有

(15)

针对本文的减振系统，假定参数变化符合均匀分布[11]，其变化范围如表1所示。根据表1中的参数分布，利用Latin超立方采样方法生成抽样数据，这里取7 000个采样点，构造一个7 000×5阶的参数矩阵，将参数矩阵传递给改进的分块增维精细积分法程序计算输出响应向量，并采用蒙特卡洛方法[12]计算减振系统各参数的一阶灵敏度和总灵敏度，一共计算10次，取均值为最终结果，如表2所示。为了直观起见，用直方图的形式来表示表2结果，如图5所示。表中的灵敏度数值出现负值是由于采样点数还不够多，但这并不影响对参数灵敏度的判断[13]。

表1　参数变化范围

表2　灵敏度计算结果

图5　减振系统各参数的全局灵敏度 Fig.5 The global sensitivityof the vibration-reduction system parameters

一阶灵敏度反映的是单个参数的变化对输出的影响；而总灵敏度不仅反映了该参数单独变化，还反映了与其它参数交互作用对输出的影响。如果得到的总灵敏度数值上和一阶灵敏度差别很大，说明参数的交互作用明显。观察图5，各参数的一阶灵敏度和总灵敏度差别并不是很大，说明参数之间交互作用不明显。各参数的灵敏度从大到小依次为K2、C2、C1、Ks、Kz。Kz对输出结果基本没有影响，因此，参数优化时将其设为定值。

4减振系统参数优化

采用遗传算法对减振系统进行参数优化，首先要给出优化计算的目标函数和参数变化范围，然后在参数变化范围内对目标函数进行寻优计算，获得优化结果。针对本文的减振系统，以担架台垂向振动加权加速度均方根值为优化目标，其计算公式如式(14)所示。参数的变化范围如表3所示。具体计算时，对遗传算法的参数设置如NSGA-Ⅱ算法，并加入线性约束条件：{Ks

表3　参数变化范围

经过计算，可得优化前后参数对比如表4所示。为了检验优化计算的效果，将优化前后担架台垂向振动加速度功率谱密度进行对比，如图6所示。由表4可知，经过参数优化，担架台垂向振动加权加速度均方根值由原来的0.5210 下降为0.4183 ，降幅达19.7%。由图6可知，参数优化后，担架台在45~55Hz范围内的振动能量明显降低，其能量峰值由原来的0.1008m2/s3下降为0.0208 m2/s3，降幅达79.4%。综合以上分析，参数优化使减振系统的动态性能得到了明显改善，这对于提高急救车内伤病员的乘坐(卧)舒适性具有重要意义。

表4　优化前后参数对比

图6　优化前后担架台垂向振动 加速度功率谱密度对比 Fig.6 The comparison of power spectral density

5结论

针对履带急救车非线性减振系统动态性能优化问题，本文首先提出了一种多目标参数辨识方法，并应用该方法辨识了急救车减振系统的物理参数，然后在灵敏度分析基础之上对减振系统进行了参数优化，有效地改善了车内乘员的乘坐(卧)舒适性。本文研究内容的完整性和严谨性对于同类研究具有很强的借鉴意义，所提出的多目标参数辨识方法很好地解决了随机激励条件下的系统辨识问题，具有较高的应用价值。

参考文献

[1]Ghanem R, Romeo F. A wavelet-based approach for model and parameter identification of non-linear systems[J]. International Journal Non-linear Mechanics, 2001,36(5): 835- 859.

[2]Pacheco R P, Steffen V.On the identification of non-linear mechanical systems using orthogonal functions[J]. International Journal Non-linear Mechanics, 2004, 39(7):1147-1159.

[3]徐崇刚，胡远满，常禹，等．生态模型的灵敏度分析[J]．应用生态学报，2004，15(6)：1056-1062．

XU Chong-gang, HU Yuan-man, CHANG Yu, et al. Sensitivity analysis in ecological modeling[J]. Chinese Journal of Applied Ecology, 2004, 15(6): 1056-1062.

[4]Morris M D. Factorial sampling plans for preliminary computational experiments[J].Technometrics,1991,33(2): 161-174.

[5]尹俊杰，常飞，李曙林，等．基于Sobol法的整体翼梁损伤容限设计参数灵敏度分析[J]．空军工程大学学报(自然科学版)，2013，14(6)：9-12．

YIN Jun-jie, CHANG Fei, LI Shu-lin, et al. Analysis of parameter sensitivity on damage tolerance design of overall beam based on sobol method[J]. Journal of Air Force Engineering University(Natural Science Edition), 2013, 14(6): 9-12.

[6]葛根，王洪礼，谭建国．多自由度非线性动力方程的改进增维精细积分法[J]．天津大学学报，2009，42(2)：113-117．

GE Gen, WANG Hong-li, TAN Jian-guo. Improved increment-dimensional precise integration method for the nonlinear dynamic equation with multi-degree-of-freedom[J]. Journal of Tianjin University, 2009,42(2): 113-117.

[7]Kalyanmoy D, Amrit P, Sameer A, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions On Evolutionary Computation, 2002,6(2): 182-197.

[8]李玥．基于多目标遗传算法的航空发动机多目标优化控制[D]．南京：南京航空航天大学，2007:6-23．

[9]杨猛，徐新喜，苏琛，等．履带急救车非线性减振系统振动特性及运动稳定性分析[J]．振动与冲击，2013，32(17)：183-188．

YANG Meng, XU Xin-xi, SU Chen, et al. Vibration characteristics and motion stability of a tracked ambulance nonlinear vibration-reduction system[J]. Journal of Vibration and Shock, 2013, 32(17): 183-188.

[10]苏琛，徐新喜，高振海，等．某履带急救车减振效率及乘卧舒适性分析[J]．振动、测试与诊断，2012，32(5)：854-857．

SU Chen, XU Xin-xi, GAO Zhen-hai, et al. Analysis on two level damping efficiency and recumbent comfort for tracked emergency ambulance[J].Journal of Vibration, Measurement & Diagnosis, 2012,32(5):854-857.

[11]刘伟，曹刚，翟红波，等．发动机管路卡箍位置动力灵敏度分析与优化设计[J]．航空动力学报，2012，27(12)： 2756-2762．

LIU Wei, CAO Gang, ZHAI Hong-bo, et al. Sensitivity analysisand dynamic optimization design of supports’ positions for engine pipelines[J]. Journal of Aerospace Power, 2012, 27(12): 2756-2762.

[12]张晓航．防空导弹武器装备体系作战效能全局敏感性分析方法研究[D]．长沙：国防科学技术大学，2010：29-36．

[13]陈刚，汪玉，毛为民，等．冲击载荷作用下舰艇管路系统全局参数灵敏度分析[J]．振动与冲击，2007，26(3)：45-48.

CHEN Gang, WANG Yu, MAO Wei-min, et al. Global parameter sensitivity analysis of shipboard piping systems under shock loads[J]. Journal of Vibration and Shock, 2007, 26(3)：45-48.

附录1：

R2=(Kzl1/J1)[(x1-x2)-l1(f1-f2)]3-(Kzl1/J1)[(x1-x2)+l1(f1-f2)]3，R3=(Kz/M2)[(x1-x2)-l1(f1-f2)]3+

附录2：

序号KsKzC1K2C2fun1fun21219485.916625411.44371457130.424835466.164429181.56250.12390.11882219649.265623205.32021457124.840037006.796728856.99100.12380.17273219594.645923893.25821457117.384036402.460829251.30890.12380.14784219605.021823766.26771457123.804136507.533328999.74810.12380.15195215076.499229060.43691456810.595434343.584732052.15360.12450.10186219640.810723323.28271457124.644436916.382628986.74770.12380.16877219629.890723664.63851457122.363236642.215429082.24780.12380.15718219160.630726307.02821457082.229535066.757931600.61720.12390.11129219603.062124156.77651457117.441036229.287329217.61290.12390.141410197279.012331040.80931456664.671034440.963231936.03720.12590.097111217324.756827417.88971457008.786634550.334031833.46890.12400.107712219501.477724421.57611457128.367036043.827129543.57710.12390.135013219555.941024373.55911457119.317535964.088529219.81470.12390.133014211934.603025686.10571456863.838435072.224929216.31820.12390.114915219557.521724530.03981457124.366835884.146729046.83190.12390.130416196567.706732215.52201456629.571134121.194132167.54030.12630.094717219524.579425021.85951457125.069935639.987729116.87080.12390.123318219459.596825516.67751457134.517035072.182729256.82360.12390.115519219523.202324148.76471457116.725136221.716329426.83930.12390.141220215666.925430126.89581456730.805834259.575930430.98790.12500.098621219608.515823470.58971457122.889336772.664628961.02600.12380.162622219565.104923831.96241457122.568736375.443429377.33570.12390.147023219573.072723968.47851457119.569636294.519728946.98150.12390.144024219562.143324195.62741457117.526636115.048229505.63090.12390.137725217435.847927591.17731457010.410734758.246830932.05200.12420.105226219624.021723670.51411457122.483636586.243329102.39010.12380.155027219507.124224828.35411457131.060535716.945529197.02860.12390.125628219649.270223205.33121457124.851537006.843628856.99900.12380.172729219636.840523461.66921457122.243336822.750329067.06820.12380.164630219579.522524723.06591457096.853735850.712329439.81050.12390.1290

注：加粗行为最优点对应数据。