杆中导波声弹敏感模态与激励频率的确定方法

杆中导波声弹敏感模态与激励频率的确定方法

刘飞1，吴斌2，何存富2，赵满全1，郁志宏1

(1.内蒙古农业大学机电工程学院，呼和浩特010018； 2.北京工业大学机械工程与应用电子技术学院，北京100124)

摘要：基于超声导波声弹性效应检测波导结构的应力水平具有潜在的优势。为实现超声导波声弹应力检测的关键技术——检测模态与激励频率的选取，提出一种基于Murnaghan超弹模型的有限元特征频率法。使用该方法计算预应力杆中的频散特性，得到反映不同激励频率应力敏感性的声弹频散曲线，与文献中的L(0,1)模态试验结果进行对比，趋势一致，说明该方法的适用性。为进一步验证该方法的可靠性，选取L(0,1)模态声弹敏感的几组频率，在自制拉伸试验平台上，对碳素钢杆进行超声导波声弹试验。试验结果表明：低应力区域误差较大，在高应力区域误差均低于10%，且声弹常数与理论结果趋势一致。研究表明该理论方法可指导超声导波声弹应力检测时频率与模态的选取。

关键词：导波；声弹性效应；特征频率法；频散特性；预应力

中图分类号:TU378；TB132文献标志码：A

基金项目：国家863计划项目(2011AA11A265); 国家自然科学基金(51205290); 中央高校基本科研业务费专项资金项目(1700219118)

收稿日期：2013-11-08修改稿收到日期：2014-01-02

基金项目：国家自然

收稿日期：2013-09-10修改稿收到日期：2013-12-12

Determination of surveying mode and excitation frequency for waveguard structure stress measurement by use of acoustoelastic effect of guided waves in bar

LIUFei1,WUBin2,HECun-fu2,ZHAOMan-quan1,YUZhi-hong1(1.College of Mechanical and Electrical Engineering, Inner Mongolia Agricultural University, Huhhot 010018, China；2. College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124, China)

Abstract:The method of measuring the stress level of waveguide structures by use of the acoustoelastic effect of ultrasonic guided wave is of potential advantages. In order to select the optimal surveying mode and excitation frequency in acoutoelastic stress testing, a finite element eigenfrequency method based on the Murnaghan hyperelastic model was presented. The dispersion characteristic of a prestressed bar was calculated using this approach, and the acoustoelastic dispersion curve was obtained for describing the stress sensitivity under different excitation frequencies. The results are consistent with those in other literatures. On this basis, selecting the surveying mode and excitation frequency, the acoustoelastic effect of L(0,1) mode was inspected for Q235 carbon steel bar on a homemade tensile test platform. The results show that: the errors are great in low stress region whereas, in high stress region it can be controlled within 10%, and the tendency of acoutoelastic constants is in agreement with the theoretical results. The study proposes a method that can provide a determination method of surveying mode and excitation frequency for stress measurement by using the acoustoelastic effect of ultrasonic guided wave.

Key words:guided waves; acoustoelastic effect; eigenfrequency method; dispersion; prestress

基于超声导波的声弹性效应对结构的应力状况进行检测是近年来新发展起来的一项技术。它主要是利用超声导波传播的速度与应力之间的关系，通过测量传播速度的变化值实现应力的估计[1]。由于该方法可以量测结构中的绝对应力水平，且配合空气耦合、电磁声等换能器还可实现非接触式测量，同时兼具测量范围广、检测精度高，能对结构的缺陷进行无损检测等优点[2]，因而，开展超声导波声弹应力检测技术的研究具有广泛的工程应用前景。

国内外许多学者已在多个领域对该技术的应用进行了深入研究。Chen[3]首次利用超声导波声弹性技术检测预应力杆中的工作应力，并得到了L(0,1)模态随应力的增大而群速度降低的结论。Di Scalea等[4-5]在前人的基础上，进一步研究了纵向模态在不同预应力水平下钢绞线中的传播特性，用Gabor小波变换方法对数据进行分析处理，取得了较好的结果。Philip等[6-7]学者利用半解析有限元在激励频率为100 kHz时，对受轴向载荷无缝钢轨(CWR)中的超声导波传播特性进行了研究，在理论上证实了这一方法的可行性，并分析了温度对弹性模量影响的敏感性。何文等[8-9]对锚杆的工作载荷和螺柱轴向应力的导波声弹性效应，利用体波等效弹性常数法进行了研究，并提出利用纵向模态和弯曲模态相结合的方法检测在役螺柱的轴向应力。刘增华等[10]利用自制的磁致伸缩传感器，对7芯预应力钢绞线中超声导波声弹性效应进行了试验研究，得到激励频率为160 kHz时，L(0,1)模态的群速度和应力之间的关系曲线。

由于超声导波的多模态与频散特性，导波模态与激励频率的选择对超声导波应力敏感性影响显著。如何确定声弹性效应最敏感的模态与所对应的激励频段就显得尤为重要。

本文在借鉴前人研究的基础上，提出一种基于Murnaghan超弹模型的特征频率法。对预应力杆中超声导波的频散特性进行了计算，得到反映声弹敏感性随导波模态与激励频率变化的声弹频散曲线，并与文献试验结果进行了对比验证。通过选取L(0,1)模态频散较小频段的多组激励频率，在自制拉伸试验平台上对声弹特性进行测量，评估应力检测精度，同时与理论方法得到的结果进行对比，验证此方法的正确性。

1预应力频散计算方法

由于杆类结构受力状况多是沿轴向或长度方向的单轴应力，假设预变形是均匀的且是单轴的，考虑材料为Murnaghan超弹性体[11]，可计算得到受单轴应力后的等效二阶弹性常数为:

(1)

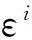
其中：

C1111=C2222=C3333=λ+2μ，

C1122=C1133=C2233=λ，C2323=C1313=C1212=μ，

C111111=2l+4m，

C112233=2l-2m+n，C112323=m-n/2，

C111122=2l，C111313=m，C231321=n/4

m，l，n是Murnaghan三阶弹性常数。

基于以上参数，利用有限元法建立的单元体应变位移关系矩阵与弹性矩阵分别为[12]：

(3)

式中：D是对称矩阵，在这里

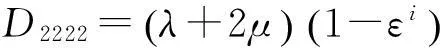
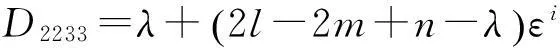
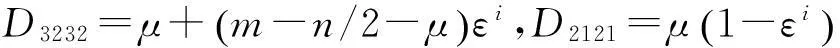
关于此模型利用特征频率法的求解方法及相速度和群速度的计算方法可参见文献[13]，本文不再进行详细论述。

2杆中超声导波声弹特性

超声导波与体波声弹特性的最大差异是受模态与激励频率的影响显著。分析预应力状态下超声导波的频散特性，通过与无应力时的频散特性进行对比，即可实现声弹频散特性的分析。本节利用上述方法，对杆中常见纵向模态与弯曲模态的声弹特性进行计算。

2.1预应力杆中超声导波频散特性

由于纵向模态具有轴对称性，可利用二维轴对称模型计算纵向模态的频散特性。预应力以预定位移的方式施加在端面或者以初始应力与应变的方式施加在模型中。弯曲模态编号一般表示为F(n,m)，其中n表示周向阶次，从截面对称性来看，表示的是反对称面的个数，亦即弯曲方向的个数；m表示轴向阶数，与纵向模态的模态分类方法是一致的。在所有弯曲模态中，由n=1定义的那一族是最重要的，即模态只沿一个方向弯曲[14]。本文只考虑这一族弯曲模态的声弹特性。因此，弯曲模态的计算可由四分之一杆模型实现，其中两径向切面分别设置为对称平面与反对称平面，端面的设置方式与纵向模态相同。

本文计算模型长度L和半径r分别是800 mm和9 mm，加载应力为200 MPa，纵向模态网格单元采用边长为0.5 mm的四边形单元，弯曲模态采用最大网格尺寸为0.5 mm的六面体单元。材料选用与文献试验材料一致的1018号钢，密度ρ=7 843 kg/m3，其弹性常数为：λ=105.4 GPa,μ=83.4 GPa,l=-69 GPa,m=-574GPa,n=-670 GPa[15]。

选择计算的频率范围在400 kHz以下，利用Pochhammer频率方程求解可知，在该频率范围内存在的纵向模态主要有L(0,1)，L(0,2)和L(0,3)模态，存在的弯曲模态主要有F(1,1)，F(1,2)和F(1,3)模态。得到的具有初始应力与无应力对应的频散曲线如图1所示。

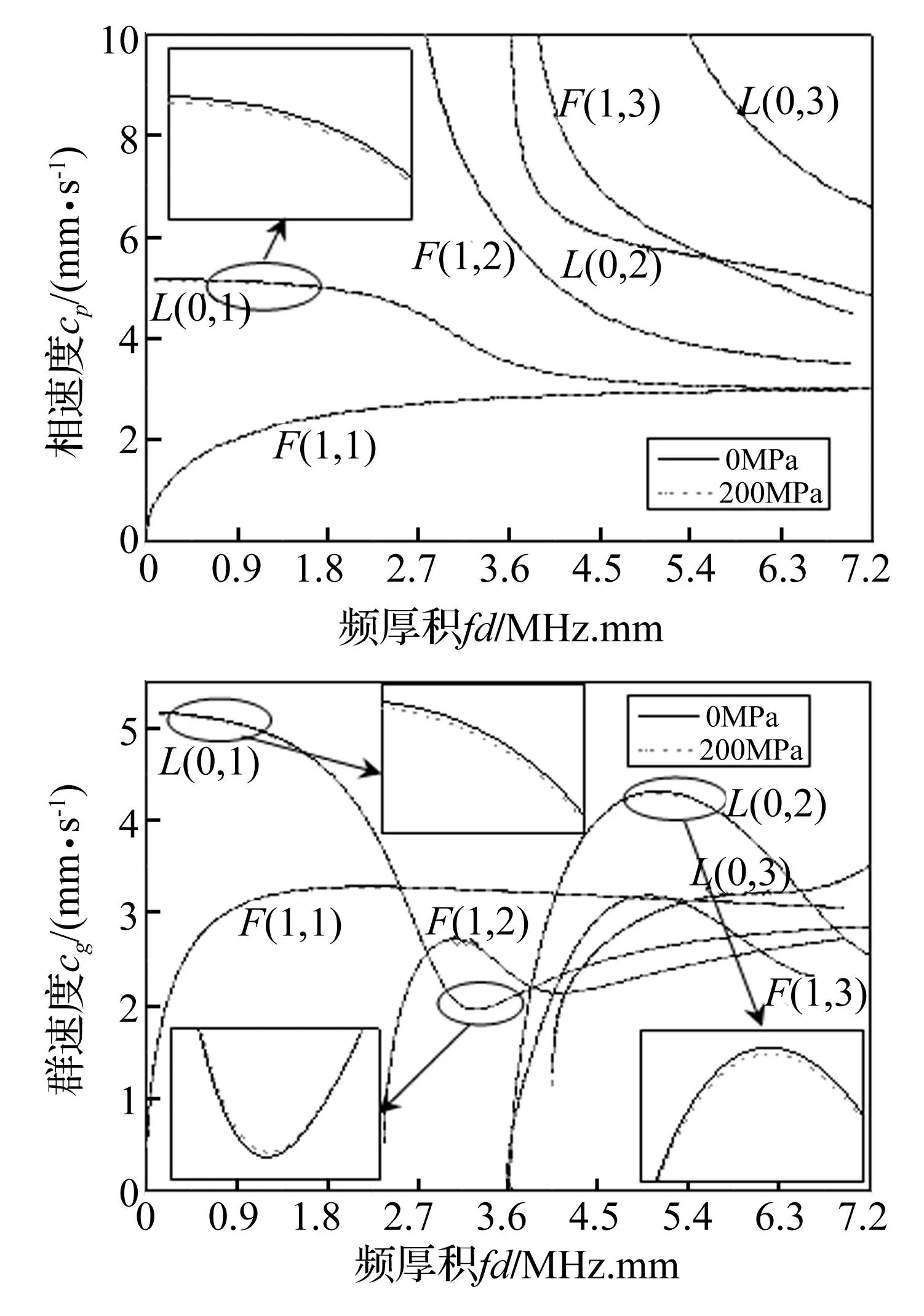
图1　不同应力水平钢杆频散曲线 Fig.1 Dispersion curves of steel bar at different stress levels

2.2超声导波声弹敏感性分析

从图1的结果可看到，在具有初始应力时，各个模态的速度变化较微弱，并不能直接观察到频率与声弹性效应的关系。因而通过选取计算频率点，对相邻特征频率进行线性插值计算对应的相速度与群速度，采用式(4)分别计算各个频率点相速度和群速度相对变化率决定的声弹性常数，并绘制声弹性常数频散曲线来反映频率与声弹性效应的关系，结果如图2所示。

(4)

式中：cσ为应力σ时的速度值，c0为无应力时的速度值。

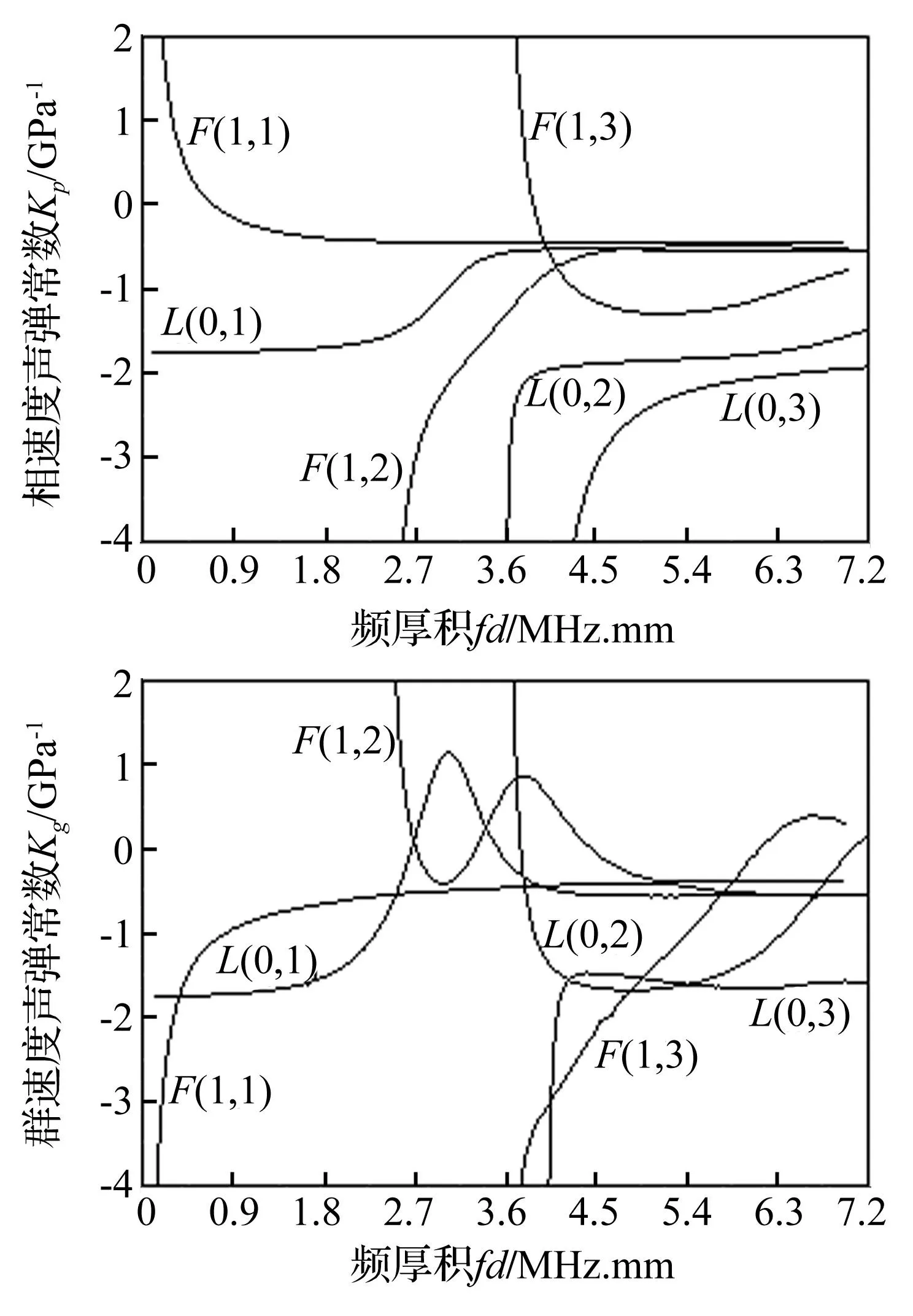
图2　钢杆中纵向模态与弯曲模态的声弹频散特性 Fig.2 Acoustoelastic dispersion for longitudinal and flexural mode

图3　钢杆中L(0,1)模态不同激励频率声弹效应 Fig.3 Variation of the acoustoelastic effect with the excitation frequency for L(0,1) mode

为验证该方法求解的预应力频散关系是否正确，本文通过与文献[16]试验得到的结果进行对比分析。根据频厚积的关系，分别选取L(0,1)模态激励频率点为88 kHz(100 kHz), 132 kHz (150 kHz), 150 kHz (170 kHz), 167.5 kHz (190 kHz), 190 kHz(215 kHz)和264.5 kHz (300 kHz)，由图2群速度声弹常数结果计算各个频率点群速度的相对变化率，结果如图3所示。

图示结果与文献试验得到的结果对比表明：频率对声弹性效应的敏感性趋势完全一致，只是在群速度相对变化率数值上有一些差别，这可能是由于材料的不一致性且在理论计算时没有考虑材料的织构效应造成的，而材料织构效应与声弹性效应对速度变化的影响是在同一个量级[17]。说明利用超弹模型的特征频率法求解预应力结构的频散关系进而选取声弹效益敏感的模态与激励频率是可行的。

因而，可得到以下结论：纵向模态均存在声弹性效应敏感的几个频段。L(0,1)模态群速度声弹性常数在频厚积为3.06 MHz.mm时出现拐点，此时声弹性常数为正，表现为在该频厚积附近群速度随拉应力的增大而递增，且存在无声弹性效应的频率点，这与体波的声弹性效应相比具有较大的差异。结合图1得到的频散曲线，选取频散较弱，声弹性效应较强的模态与所对应的频厚积作为杆中超声导波声弹应力检测的最优选择，可知L(0,1)模态在频厚积低于1.44 MHz.mm时，L(0,2)模态在4.23~5.4 MHz.mm时，L(0,3)模态在5~6.48 MHz.mm时，均适合于声弹应力检测。F(1,1)模态在频散较小的区域声弹性效应较弱，而F(1,2)模态与F(1,3)模态由于很难实现单一模态的激励，在实际检测中并不常用，因而说明弯曲模态相比纵向模态并不适合用于声弹应力检测。

3钢杆中超声导波声弹效应试验研究

3.1试验系统与测量方法

超声导波声弹测量系统如图4所示。主要包括函数发生器、示波器、压电陶瓷片、拉伸装置与锚具等。由于频率对声弹效应的影响只与材料的二阶弹性常数有关，而钢材的二阶弹性常数较为接近，故在试验时选取国内最为常见的Q235碳素钢，以评估不同激励频率的声弹敏感性，试件直径为12 mm。

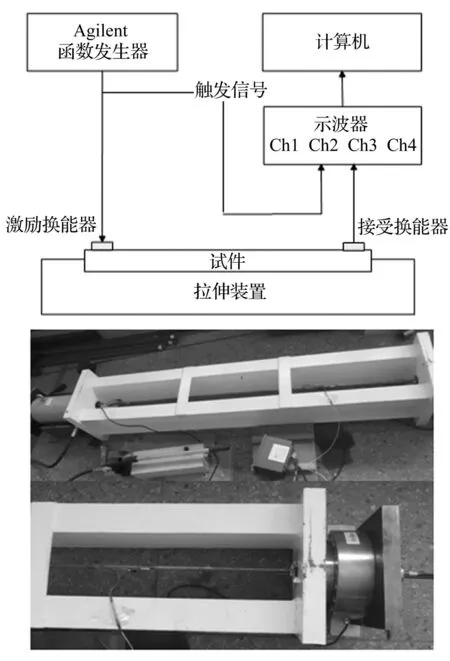
图4　超声导波声弹拉伸系统实物图 Fig.4 Measurement system schematic and picture

试件通过锚具固定在拉伸装置中，在拉伸装置中固定有数显压力传感器，可精确测量施加的应力水平。拉力从0 t加载到2 t，对应最大载荷为屈服极限的75%，每加载0.2 t采集一次数据。采用压电陶瓷片是鉴于其换能效率高，对信号较为灵敏，且信噪比高，从而无需在测试系统中添加功率放大器，可提高系统的稳定性。由于直接测量群速度存在一定的误差，采用式(4)计算的声弹常数并不准确。为克服上述误差，考虑到有应力和无应力时传播的时间相对于时延值二者非常接近，即声弹常数计算可由式(5)表示：

(5)

式中：Δtσ为时延值，L为两传感器间的有效拉伸长度，ΔL有效拉伸长度对应的伸长量。

对式(5)进行变形，即可得到试验声弹常数的计算公式如式(6)所示，其中时延值通过互相关函数法计算有应力和无应力时直达波的信号数据得到。

(6)

式中： E为材料的杨氏模量。

3.2L(0,1)模态声弹试验结果及分析

选取中心频率为120kHz的长度伸缩性压电陶瓷片对L(0,1)模态声弹敏感频段进行声弹试验研究。利用压电片的自身带宽属性，分别激励96kHz，120kHz和140kHz三组频率，进行加卸载试验。计算各个应力点的时延值与群速度相对变化率，图5为频率在120kHz时无载荷与2t拉力加载的信号对比及互相关分析结果。

信号对比结果表明：接收到的原始信号模态单一，无掺杂端面回波成分，适合声弹时延计算；在声弹试验时，随拉力增加信号幅值会升高。为评估L(0,1)模态在各频率点的声弹常数与应力灵敏度，对所有加载点进行互相关运算，计算时间延迟与拉力之间的关系式，结果如图6所示。

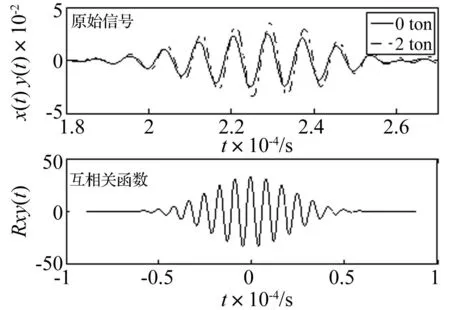
图5　互相关分析结果 Fig.5 Cross-correlation analysis results

由图6结果可知，加载和卸载的线性度较好，且二者也具有较高的一致性。根据加卸载线性拟合斜率的平均值计算声弹常数，并使用该声弹常数评估各个应力点的误差。结果可知：96kHz的声弹常数为-0.012 5GPa-1,用此声弹常数评估的应力值在低应力区域最大误差高于40%，而在拉力大于1t时，试验

结果的误差均低于10%；120kHz的声弹常数为-0.009 8GPa-1, 加载误差较小，当拉力大于0.8t时的误差均小于5%，而卸载误差较大，结果与96kHz的趋势一致；140kHz的声弹常数为-0.006 3GPa-1， 加卸载的误差在低应力区域最高达53.7%，而在拉力为1t以上时，误差均小于10%。以上结果表明超声导波声弹效应适宜评估结构应力是否超载，而不适合检测结构预应力是否缺失。同时发现随频率的增大，时间延迟降低，表明L(0,1)模态在此频段内声弹性效应是逐渐降低的，这与理论得到的结论是吻合的，且声弹常数量值也与国外文献报道的结果[15-17]较为一致。进一步说明了有限元特征频率法求解预应力频散关系的可靠性，表明理论计算的声弹常数可以作为模态与激励频率选取的依据。但鉴于理论模型与实际材料特性的差异，理论声弹常数不可作为标定值去指导工程实测。

图6　群速度相对变化率与加载应力的关系 Fig.6 Relative group velocity change as a function of load stress

4结论

本文基于Murnaghan超弹模型的特征频率法，提出一种计算预应力结构频散关系的方法，并用该方法计算了纵向模态与弯曲模态的声弹频散特性，得到如下结论：

(1)计算L(0,1)模态在不同激励频率点的声弹常数，与文献试验得到的结果进行了对比，趋势一致，验证了该方法的可行性。

(2)通过计算预应力结构的频散关系，得到反映应力敏感性的声弹频散曲线。

(3)利用自制的拉伸试验平台，对L(0,1)模态声弹敏感频段的几组频率进行了声弹常数测量，试验结果线性度较好，与理论方法得到的声弹常数趋势一致，进一步说明理论方法是可靠的。

(4)利用测得的声弹常数评估各个应力点误差可知，在低应力区域误差较大，而在高应力区域误差均可控制在10%以内，表明超声导波声弹效应适宜评估结构应力是否超载，而不适合检测结构预应力是否缺失。

综上所述，该方法可有效地指导超声导波声弹应力检测时模态与激励频率的优化选取。但鉴于理论模型与实际材料特性的差异性，理论计算的声弹常数不可作为标定声弹常数去指导工程实测。

参考文献

[1]ChakiS,BourseG.Guidedultrasonicwavesfornon-destructivemonitoringofthestresslevelsinprestressedsteelstrands[J].Ultrasonics, 2009, 49(2): 162-171.

[2]何存富，吴斌，范晋伟. 超声柱面导波技术及其应用研究进展[J]. 力学进展, 2001, 3(2)：203-214.

HECun-fu,WUBin,FANJin-wei.Advancesinultrasoniccylindricalguidedwavestechniquesandtheirapplications[J].AdvancesinMechanics, 2001, 3(2)：203-214.

[3]ChenHLR,HeY,RaoG.Measurementofprestressforceintherodsofstressedtimberbridgesusingstresswaves[J].Mater.Eval, 1998,56 (8) :977-981.

[4]DiScaleaFL,RizzoP,FriederS.Stressmeasurementanddefectdetectioninsteelstrandsbyguidedstresswaves[J].JournalofMaterialsinCivilEngineering, 2003, 15(3)：219-227.

[5]RizzoP,DiScaleaFL.Ultrasonicinspectionofmulti-wiresteelstrandswiththeaidofthewavelettransform[J].SmartMaterialsandStructures, 2005, 14(4)：685-695.

[6]LovedayPW.Semi-analyticalfiniteelementanalysisofelasticwaveguidessubjectedtoaxialloads[J].Ultrasonics, 2009,49: 298-300.

[7]LovedayPW,WilcoxPD.Guidedwavepropagationasameasureofaxialloadsinrails[C].ProceedingsofSPIE-TheInternationalSocietyforOpticalEngineering, 2010, 7650(23):1-8.

[8]何文,王成,宁建国,等. 端锚锚杆工作载荷的导波确定法[J]. 岩石力学与工程学报, 2009, 28(9):1767-1772.

HEWen,WANGCheng,NINGJian-guo,etal.Guidedwavedeterminationmethodofserviceloadinpartiallygroutedbolt[J].ChineseJournalofRockMechanicsandEngineering, 2009, 28(9):1767-1772.

[9]何文,王成. 基于导波技术的螺柱轴力无损检测[J]. 计算力学学报, 2009, 26(4):604-607.

HEWen,WANGCheng.Guidedwavenondestructivetestingofaxialstressinthestud[J].ChineseJournalofComputationalMechanics, 2009, 26(4):604-607.

[10]刘增华,刘溯,吴斌,等. 预应力钢绞线中超声导波声弹性效应的试验研究[J]. 机械工程学报, 2010,46(2):22-26.

LIUZeng-hua,LIUSu,WUBin,etal.Experimentalresearchonacoustoelasticeffectofultrasonicguidedwavesinprestressingsteelstrand[J].JournalofMechanicalEngineering, 2010,46(2):22-26.

[11]PaoYH,SachseW,FukuokaH,Acoustoelasticityandultrasonicmeasurementofresidualstress[J].PhysicalAcoustics,NewYork,AcademicPress, ⅩⅦ, 1984: 62-140.

[12]MaceBR,DuhamelD,BrennanMJ,etal.Finiteelementpredictionofwavemotioninstructuralwaveguides[J].JournaloftheAcousticalSocietyofAmerica, 2005, 117(5): 2835-2843.

[13]吴斌，刘飞，何存富. 波导结构频散分析的特征频率法及在板条结构中的应用[J]. 计算力学学报, 2013, 30(4):514-519.

WUBin,LIUFei,HECun-fu.Analysisofdispersioncharacteristiceigenfrequencymethodforwaveguidesandapplicationinplatestrip[J].ChineseJournalofComputationalMechanics, 2013, 30(4):514-519.

[14]ROSEJL.固体中的超声波[M]. 何存富，吴斌，王秀彦译. 北京：科学出版社，2004.

[15]TakahashiS,MotegiR.Stressdependencyonultrasonicwavepropagationvelocity:Part2Thirdorderelasticconstantsofsteels[J].Journalofmaterialsscience. 22(1987):1857-1863.

[16]RizzoP,Di-ScaleaFL.Effectoffrequencyontheacoustoelasticresponseofsteelbars[J].Exp.Tech, 2003: 40-43.

[17]WasherGA,Theacoustoelasticeffectinprestressingtendons[D].PhDthesis,JohnsHopkinsUniversity, 2001.

[18]ChenHL,WissawapaisalK.Measurementoftensileforcesinaseven-wireprestressingstrandusingstresswaves[J].JournalofEngineeringMechanics, 2001, 127(6):599-606.

第一作者于蓬男，博士生，1986年生

通信作者章桐男，教授，博士生导师，1960年生

邮箱：tzhang@fcv-sh.com

第一作者杨超男，博士生，1988年2月生

通信作者肖守讷男，研究员，1964年6月生