粘弹性介质中输流碳纳米管的动态稳定性分析

粘弹性介质中输流碳纳米管的动态稳定性分析

梁峰， 包日东， 金莹， 苏勇

(沈阳化工大学 能源与动力工程学院，沈阳110142)

摘要：应用非局部粘弹性夹层梁模型分析粘弹性介质中输送脉动流碳纳米管的动态稳定性。在经典的欧拉梁模型中考虑了由管道内、外壁上的薄表面层引起的表面弹性效应和表面残余应力，同时考虑纳米管道的非局部效应，得到了改进的欧拉梁模型。用平均法对其控制方程进行求解，得到了管道稳定性区域。数值算例揭示了纳米管的壁厚、粘弹性特性、表面效应及两个介质参数对管道动态稳定性的复杂影响，结论可为纳米流体机械的结构设计和振动分析提供理论基础。

关键词：输流碳纳米管；稳定性；参数共振；表面效应；粘弹性介质

中图分类号:O326文献标志码：A

Dynamicstabilityofafluid-conveyingcarbonnanotubeembeddinginlinearviscoelasticmedium

LIANG Feng, BAO Ri-dong, JIN Ying, SU Yong(SchoolofEnergyandPowerEngineering,ShenyangUniversityofChemicalTechnology,Shenyang110142,China)

Abstract:A nonlocal viscoelastic sandwich-beam model was developed to investigate the dynamic stability of a pulsating-fluid-conveying carbon nanotube (CNT) embedding in linear viscoelastic medium. The classical Euler-Bernoulli beam model was modified by considering the effects of surface elasticity and surface residual stress induced by thin surface layers presented on the inner and outer tube walls. The nonlocal effect of CNT was also taken into account. The governing equation was solved via the averaging method and the stability regions were obtained. Numerical examples were presented to reveal the complicated influences of tube thickness, viscoelasticity, surface effects and two medium parameters on the dynamic stability of the CNT. The conclusions drawn in the present paper are thought to be helpful to the structural design and vibration analysis of nanofluidic devices.

Keywords:fluid-conveyingcarbonnanotube;stability;parametricresonance;surfaceeffect;linearviscoelasticmedium

碳纳米管是1991年被发现的一种重要的纳米材料。研究表明，碳纳米管具有十分优异的力学、电磁学和化学性能，其强度是钢的100倍，是已知材料中最高的，但密度仅为钢的1/6，无论是强度还是韧性都远远优于任何已知纤维材料。碳纳米管作为复合材料的增强体，表现出了良好的强度、弹性、抗疲劳性，同时还具有耐强酸、强碱，在空气中973K以下基本不被氧化等优良性质。目前，碳纳米管已经在物理、化学、生物、电子和材料等领域得到了广泛的研究和应用。

由于碳纳米管具有小尺度、低密度、高强度和高硬度等特性，加之完美的空心圆柱形几何结构，使其成为纳米尺度下流体储藏与输运的重要载体。碳纳米管可以作为气体存储的纳米容器，输运流体的纳米管道，最小的毛细血管，纳米级化学试管等，还可以将液态金属填充在碳纳米管内部，使其成为纳米级温度计。由于碳纳米管具有良好的力学、电学和化学特性，其内壁又是极其光滑的，因此可以被用来快速和安全地输送液氢等燃料，为能源的输送提供新的解决办法。另外，植物细胞输水的过程、医学领域的药物流体在蛋白质中输送、生物体中选择性输运粒子流的特性都和碳纳米管输运流体的问题有着相似的动力学机理，都可以用碳纳米管输送流体的动力学模型来描述。

由于普通宏观管道内壁与流体间存在较大的摩擦，在管道安全运行的前提下，流体流速一般不会很大，然而Majumder等[1]通过实验发现，流体在纳米管中的流速比理论预测结果要高4-5个数量级，流体的流动速度可以达到非常大。作为一种典型的小尺度高流速流固耦合系统，输流碳纳米管常常会表现出极其丰富的动力学现象。Yoon等[2-3]应用单弹性梁模型研究了输流碳纳米管的自由振动和结构不稳定性，证明了纳米管道内部的高速流体对管道的振动频率和振幅衰减率有明显影响；基于此项研究，Wang等[4]应用多弹性梁模型研究了输流双壁碳纳米管的固有频率和屈曲失稳特性，发现其共振频率决定于流体流速，当流速达到一定值时，碳纳米管就会发生屈曲失稳；Yan等[5-6]的研究结果也证明了内部高速流体和层间的范德华力是引起输流多壁碳纳米管失稳的重要原因。但总体来说，研究碳纳米管固体力学行为[7]的文献很多，而关于碳纳米管内流体流动问题的研究则较少，有关流固耦合下，尤其是脉动内流作用下碳纳米管的动力学行为以及振动稳定性方面的研究报道就更少。随着纳米科技的发展，输流纳米结构在工业工程、生物、医疗等领域的应用日益广泛，而其力学问题也应该得到广泛关注。这也是本文研究的意义所在。

对于输流碳纳米管的力学特性研究，目前主要采用三种方法：分子动力学法[8]、实验法[9]和连续介质力学方法[10]。由于分子动力学模拟计算量非常大，对计算机处理能力的要求很高，而纳米尺度的实验常受到取材、实验设备和观测手段等条件的限制，所以，尽管连续介质力学方法对于研究分子范畴的物理现象有一定的局限，但仍然成为研究输流碳纳米管力学行为的有效且不可或缺的方法，这也必将是今后一段时期对于输流碳纳米管动力学特性研究的主流方法。自从碳纳米管被发现以来，已经有很多学者利用局部和非局部弹性理论，以连续弹性Euler梁、Timoshenko梁及壳为模型对单壁和多壁输流碳纳米管(包括直管和曲管)的力学特性进行了研究，但目前，利用这些方法对其非线性振动及脉动流作用下的稳定性问题的研究还不多见。因此，很有必要对这方面问题开展深入研究。本文应用非局部粘弹性夹层梁模型研究粘弹性介质[11](模拟周围生物组织液、化学溶剂等环境介质)中输送脉动流碳纳米管的振动稳定性问题，重点分析纳米管的壁厚、粘弹性特性、表面效应及两个介质参数对系统稳定性的影响。所得结论可为工程纳米流体机械的设计分析提供一定的理论基础。

1运动微分方程

图1(a)所示为粘弹性介质中两端固定输流碳纳米管的力学模型。假定管道只发生横向面内振动y(x, t)，x轴为管道轴线，t为时间变量，U为管内流速。K和C分别为粘弹性介质的线性模量和阻尼因子，可通过线粘弹性材料的实验测得。考虑文献[12]中的控制方程及本文中的粘弹性介质，可以得到无表面效应时输流碳纳米管系统的横向振动微分方程为：

(1)

式中：ν、EI、L、m分别为管道的KelvinVoigt型粘弹性系数、弯曲刚度、长度、单位长度的质量，e0a为表征纳米尺度效应的非局部参数；M为管内流体单位长度的质量。图1(b)和(c)分别显示了出现内、外表面层时管道的纵向和横向剖面图。通常，纳米材料的表面层会引起两种附加效应[13-15]：一种是表面弹性效应，其通常表现为弯曲刚度的增加。假定内、外表面层的杨氏模量和厚度均为Es和t0，则增加的弯曲刚度[13,15]可表示为：

(2)

式中，d和D为纳米管的内、外径，如图1(c)所示。

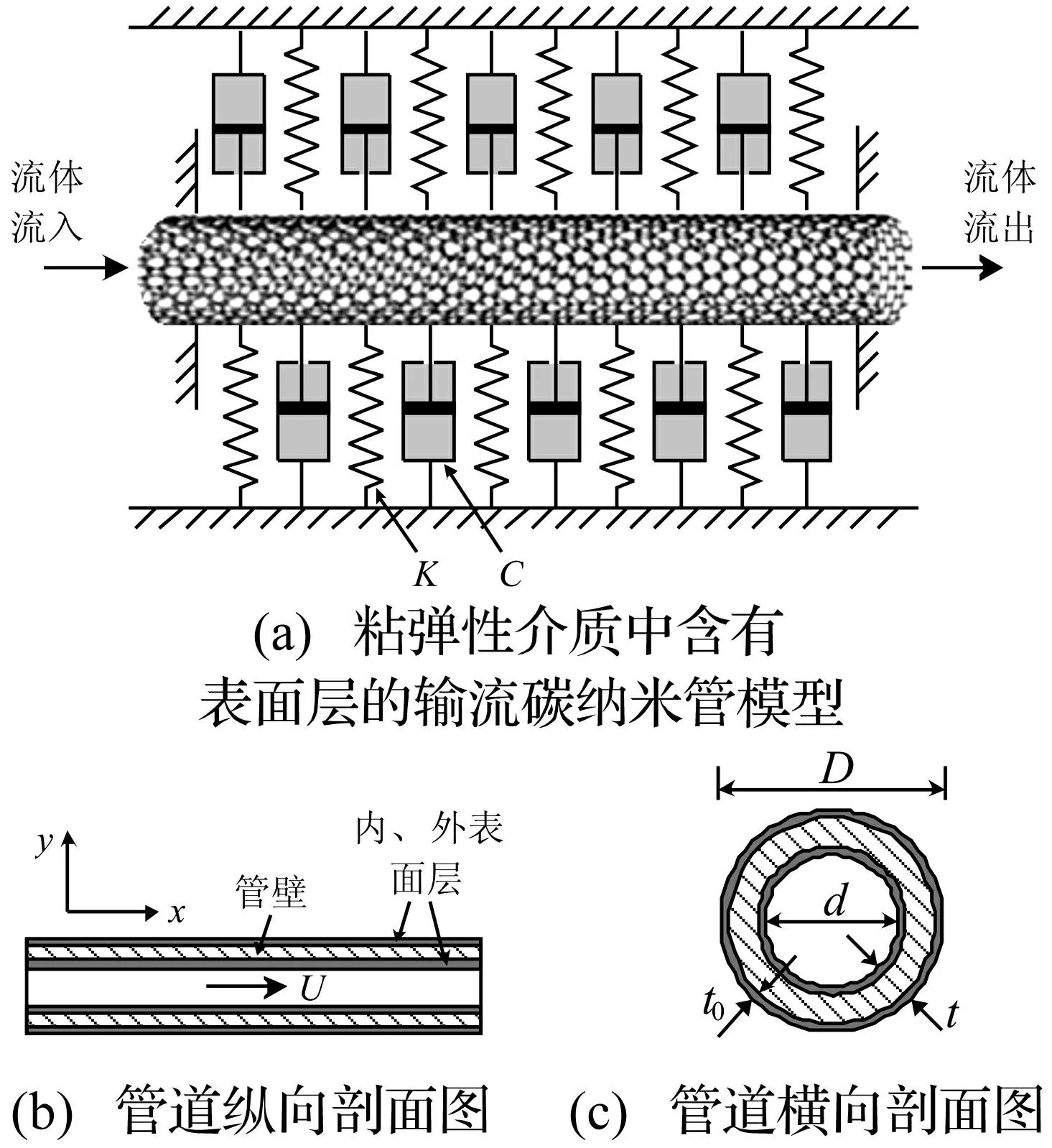
图1　系统的力学模型 Fig.1 Mechanical model of the system considered

另一种是表面残余应力，通常表现为横向分布载荷q(x)的增加[13-14]：

q(x)=Γ(∂2y/∂x2)

(3)

式中常数Γ=2τ0(d+D)，τ0为表面残余应力，可通过广义Young-Laplace方程来计算[15-16]。考虑表面层引起的这两种附加效应，方程(1)可改写为

(4)

引入无量纲变量和参数：

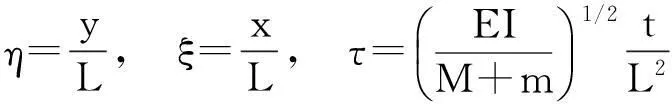
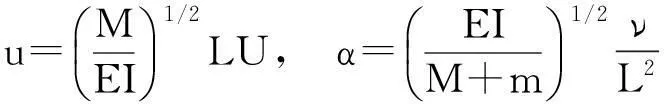
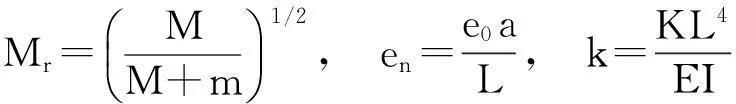
(5)

则式(4)可转化为如下无量纲形式：

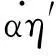
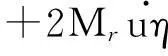
(6)

式中( )′和(·)分别表示∂( )/∂ξ和∂( )/∂τ。输流碳纳米管内微流体的驱动方式种类很多，如压力驱动、电渗驱动、电水力驱动和热驱动等等。本文考虑的输流碳纳米管，其内流可通过电渗驱动实现脉动，此时方程(6)中的流速可表示为：

u=u0[1+μcos(ωτ)]

(7)

式中u0为平均流速，ω和μ分别为无量纲脉动频率和幅值(μ≪1)。由于脉动幅值μ很小，因此介质的线性模量K和阻尼因子C沿管道长度方向可看成是均匀分布的。将式(7)代入方程(6)后用两振型Galerkin展开式：

(8)

进行离散化处理，式中qi(τ)为广义坐标，ψi(ξ)为两端固定梁的振型函数。则由振型的正交性并经适当变换后可得一阶微分方程组：

μB2qcos(ωτ)-αB3q

(9)

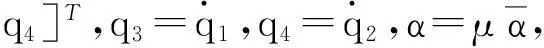
2平均化系统

(10)

z2i-1=aicosβi,z2i=aisinβi,i=1,2

(11)

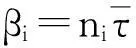
当n1=1/2时，系统平均化方程为：

(12)

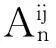
(13)

若系统不满足上式条件，则将发生第一阶主参数共振。

3稳定性分析

本节中将通过数值算例来分析碳纳米管在脉动内流作用时的动态稳定性。为便于计算，算例中采用[111]晶体方向的碳纳米管，因此其几何和物理参数取为：ρt=2700kg/m3(纳米管密度)，d=20nm，t=3nm(壁厚, t=(D-d)/2)，L/D=20 (长径比)，E=70GPa，Est0=5.1882N/m，τ0=0.9108 N/m[15]，ρw=1000kg/m3(内流密度)。其他系统参数值选为：v=5E-11s，e0a=50nm，U=500m/s，K=0.6MPa，C=1.2E-04Pas增大间距(下面各图中未具体给定的参数值均取该组数值)。

图2给出了不同壁厚t和表面参数下由式(13)确定的ω μ平面上第一阶主参数共振边界曲线。其中曲线内部为发生参数共振区域，外部为稳定区域。由图2可见(左侧3条曲线)，随着壁厚的增大，共振区域逐渐从低频向高频方向移动，说明系统共振频率升高，共振从而更难发生，也即提高了系统的稳定性。而且，共振区域越来越小，这说明对一个给定的μ值，引起参数共振的ω范围变小，即系统更加稳定。所以，适当增加纳米管壁厚会提高系统的动态稳定性。这是因为增加壁厚会增大管道刚度，从而系统固有频率和稳定性都将随之提高。

此外，图2中同时分析了表面效应对稳定性区域的影响(右侧3条曲线)。可以看出，当出现表面层以后，不仅共振区域向高频方向移动，而且共振区域也变小，即系统稳定性得到了提高。这种作用尤其在壁厚较小时更为明显。但是，表面层的出现也降低了壁厚变化对稳定性区域的影响，说明表面效应会削弱壁厚对稳定性的作用。表面效应对纳米管系统的复杂影响还可从图3中得到体现，该图取管材粘弹性系数v作为分析参数。从图中可以看出，尽管增大v值不会改变系统共振频率，但随着v值增大，共振区域逐渐变小，说明增大管材粘弹性会提高系统稳定性。而在出现表面层以后，共振区域会整体大幅向高频移动，而且共振区域会显著缩小，说明系统稳定性再次得到提高。这种作用尤其在高v值时更为明显。此外，v值变化对共振区域的影响也会因表面层的出现而增大，说明表面效应能够增强管材粘弹性对稳定性的作用。以上这些都表明了表面效应对纳米管系统稳定性的重要作用，在设计分析纳米流体机械时应重点考虑。

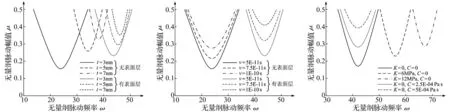
图2 不同壁厚t和表面参数下管道的稳定性区域Fig.2StabilityregionsoftheCNTfordifferenttubethicknesstandsurfaceparameters图3 不同粘弹性系数v和表面参数下管道的稳定性区域Fig.3StabilityregionsoftheCNTfordifferentviscoelasticcoefficientvandsurfaceparameters图4 不同线性模量K和阻尼因子C时管道的稳定性区域Fig.4StabilityregionsoftheCNTfordifferentlinearmodulusKanddampingfactorCofthelinearviscoelasticmediums

图4分析了纳米管外部粘弹性介质的线性模量K和阻尼因子C对系统稳定性区域的影响。由图可以看出，增大K值可以使共振区域向高频移动，且共振区域变小，说明系统稳定性提高。这是因为介质模型中的线性弹簧对管道提供了分散支承，提高K值即提高了支撑力，相当于增大了管道自身的刚度，从而使共振频率增大，共振失稳也更难发生。而增大C值虽然不会改变共振频率，但却会使共振区域大幅缩小，稳定性将会大幅增强。这是因为增大C值会使介质阻尼增大，从而使更多的振动能量被周围介质吸收，系统将更加稳定。粘弹性介质的这个阻尼效应与管材本身的粘弹性特性对系统稳定性的影响是相似的。总之，增大粘弹性介质的两个参数均可以提高输流碳纳米管系统的动态稳定性。

4结论

本文应用非局部粘弹性夹层梁模型研究了处于粘弹性介质中的输流碳纳米管的参数共振稳定性问题。通过文中分析，可得到以下结论：

(1) 适当增加纳米管壁厚和提高管材粘弹性特性可以增强系统的动态稳定性。

(2) 表面效应本身可以提高系统稳定性，而且还会增强管材粘弹性对稳定性的作用，但却会降低纳米管壁厚对稳定性的影响。

(3) 增大纳米管外部粘弹性介质的两个参数值均可以提高系统的稳定性。

综上所述，输流碳纳米管系统的动态稳定性会受到包括材料、流体及环境等在内的多个因素的影响，而这些条件之间的相互影响又是相当复杂的。因此，在设计和分析纳米流体机械时，应综合考虑各个影响因素，以保证其安全、稳定的工作。

参考文献

[1]MajumderM,ChopraN,AndrewsR,etal.Nanoscalehydrodynamics:Enhancedflowincarbonnanotubes[J].Nature, 2005, 438: 44-44.

[2]YoonJ,RuCQ,MioduchowskiA.Vibrationandinstabilityofcarbonnanotubesconveyingfluid[J].CompositesScienceandTechnology, 2005, 65(9): 1326-1336.

[3]ReddyCD,LuC,RajendranS,etal.Freevibrationanalysisoffluid-conveyingsingle-walledcarbonnanotubes[J].AppliedPhysicsLetters, 2007, 90(13): 133122.

[4]WangL,NiQ,LiM.Bucklinginstabilityofdouble-wallcarbonnanotubesconveyingfluid[J].ComputationalMaterialsScience, 2008, 44(2): 821-825.

[5]YanY,WangWQ,ZhangLX.Dynamicalbehaviorsoffluid-conveyedmulti-walledcarbonnanotubes[J].AppliedMathematicalModelling, 2009, 33(3): 1430-1440.

[6]YanY,HeXQ,ZhangLX,etal.Dynamicbehavioroftriple-walledcarbonnanotubesconveyingfluid[J].JournalofSoundandVibration, 2009, 319(3-5): 1003-1018.

[7]杨武, 彭旭龙, 李显方. 锥形纳米管纵向振动固有频率[J]. 振动与冲击, 2014, 33(2): 158-162.

YANGWu,PENGXu-long,LIXian-fang.Naturalfrequenciesoflongitudinalvibrationofcone-shapednanotubes[J].JournalofVibrationandShock, 2014, 33(2): 158-162.

[8]TuzunRE,NoidDW,SumpterBG,etal.Dynamicsoffluidflowinsidecarbonnanotubes[J].Nanotechnology, 1996, 7: 241-246.

[9]WongEW,SheehanPE,LieberCM.Nanobeammechanics:elasticity,strengthandtoughnessofnanorodsandnanotubes[J].Science, 1997, 277: 1971-1975.

[10]YangY,ZhangLX,LimCW.Wavepropagationinfluid-filledsingle-walledcarbonnanotubeonanalyticallynonlocalEuler-Bernoullibeammodel[J].JournalofSoundandVibration, 2012, 331(7): 1567-1579.

[11]张计光, 陈立群, 钱跃竑.Winkler地基上黏弹性输流管的参数共振稳定性[J]. 振动与冲击, 2013, 32(13): 137-141.

ZHANGJi-guang,CHENLi-qun,QIANYue-hong.DynamicstabilityofparametricresonanceforaviscoelasticpipeconveyingpulsatingfluidonWinklerelasticfoundation[J].JournalofVibrationandShock, 2013, 32(13): 137-141.

[12]WangL.Vibrationandinstabilityanalysisoftubularnano-andmicro-beamsconveyingfluidusingnonlocalelastictheory[J].PhysicaE, 2009, 41(10): 1835-1840.

[13]WangGF,FengXQ.Effectsofsurfaceelasticityandresidualsurfacetensiononthenaturalfrequencyofmicrobeams[J].AppliedPhysicsLetters,2007,90(23):231904.

[14]HeJ,LilleyCM.Surfacestresseffectonbendingresonanceofnanowireswithdifferentboundaryconditions[J].AppliedPhysicsLetters, 2008, 93(26): 263108.

[15]FarshiB,AssadiA,Alinia-ziaziA.Frequencyanalysisofnanotubeswithconsiderationofsurfaceeffects[J].AppliedPhysicsLetters, 2010, 96(9): 093105.

[16]ChenT,ChiuMS,WengCN.DerivationofthegeneralizedYoung-Laplaceequationofcurvedinterfacesinnanoscaledsolids[J].JournalofAppliedPhysics,2006,100(7): 074308.