具有初始几何缺陷加劲板的动态屈曲

具有初始几何缺陷加劲板的动态屈曲

马牛静1,王荣辉1,2，韩强1

(1华南理工大学土木与交通学院;2亚热带建筑科学国家重点实验室，广州510640)

摘要：针对工程中常用的加劲板，研究了动态屈曲的求解方法。将加劲板分为母板与加劲肋两个部分考虑，其中母板按经典薄板理论计算，加劲肋视为Euler梁。假定加劲板的位移，利用Hamilton原理结合系统能量和振型叠加法建立了加劲板的动态屈曲特征方程。最后，选择四边简支加劲板进行数值分析，分析中考虑初始几何缺陷的影响，并讨论了初始几何缺陷、加劲肋的数量及其刚度的变化对动态屈曲临界荷载的影响。结果表明：一阶模态的初始几何缺陷对加劲板的临界荷载影响很大，而增加加劲肋的数量及其刚度可以提高加劲板的抗动态屈曲能力。研究结果也为加劲板的结构设计方法提供一定的参考。

关键词：加劲板；初始几何缺陷；动态屈曲；临界荷载；Hamilton原理

中图分类号:O322文献标志码：A

基金项目：国家自然科学基金(51277186)

收稿日期：2013-07-24修改稿收到日期：2013-12-04

Dynamicalbucklingofstiffenedplateswithinitialgeometricalimperfection

MA Niu-jing1,WANGRong-hui1,2, HAN Qiang1(1.SchoolofCivilEngineeringandTransportation,SouthChinaUniversityofTechnology; 2.StateKeyLaboratoryofSubtropicalBuildingScience,Guangzhou510640,China)

Abstract:An approach was presented to study the dynamical buckling of stiffened plates. The stiffened plate was divided into one plate and some stiffeners, with the plate analyzed based on the classical thin plate theory, and the stiffeners taken as Euler beams. Assuming the displacements of the stiffened plate, the Hamilton principle and modal superposition method were used to derive the eigenvalue equations of the stiffened plate according to the energy of the system. Numerical examples of simply supported stiffened plates were presented to study the critical loads with the initial geometrical imperfection considered. A detailed discussion on how the initial geometrical imperfection, the number and the flexural rigidity of stiffeners influence the critical load was carried out. The results show the initial geometrical imperfection in the 1st mode shape has a great effect on the critical load, and the increase of the number and the flexural rigidity of stiffeners can strengthen the dynamical buckling capacity. These conclusions can also provide references to the engineering design of stiffened plates.

Keywords:stiffenedplates;initialgeometricalimperfection;dynamicalbuckling;criticalloads;Hamiltonprinciple

加劲板在船舶、土木、机械和宇航工程上有着广泛的应用，由于加劲板在许多情况下要承受动荷载，因此在加劲板设计中需要考虑一定的面内动荷载。在均布与非均布面内动荷载作用下，加劲板的动力行为对工程设计人员非常重要。加劲板在面内周期动荷载作用下可能发生参数共振，从而引起结构动力失稳破坏，动力失稳破坏荷载可能远远低于结构的静力屈曲荷载。

国内外学者对于加劲板的研究主要集中在静力屈曲问题上[1-4]，而对于加劲板在动荷载作用下屈曲问题的研究成果却比较少。Leipholz[5]提出了广义自共轭的概念，建立了广义的Hamilton原理，用拓展的伽辽金法解出矩形板在随从力作用下，不同边界条件下的临界力。Srivastava等[6]运用有限元法研究了加劲板在非均布面内谐波激励下的加劲板的动力稳定。Patel等[7]运用有限元法研究了加劲壳的静力与动力稳定。Srivastava等研究中均未考虑结构初始缺陷的影响，因此计算结果并不能准确地反映实际情况。张涛等[8]分析了流固冲击下加筋板的非线性弹性动态屈曲，但并未得到加劲板的动态屈曲临界荷载。此外：Huang等[9]研究了轴向时变荷载作用下功能梯度壳的非线性动力屈曲；Yang等[10]运用平均法研究了轴线加速运动Timoshenko梁的动力稳定性；Banichuk等[11]讨论了轴向运动传送带的稳定性问题；Chen[12]研究了轴向周期荷载作用下扭转Timoshenko梁的动力稳定性；程昌钧等[13]求解出粘弹性环形板的临界载荷并得出了动力稳定性的判据；莫宵依等[14]讨论了矩形薄板在非保守力作用下的动力稳定性问题；周银锋等[15]研究了随从力作用下粘弹性板的动力稳定性。韩大伟等[16]基于双特征参数法和应力波理论，求解了三边简支一边固支矩形薄板在面内轴向冲击载荷作用下动力屈曲位移的解析解。邓磊等[17]将临界应力和屈曲惯性项指数参数作为双特征参数求解，研究了面内阶跃载荷作用下矩形薄板的塑性动力屈曲问题。以上学者对梁、板、壳的动力稳定问题作了大量的研究工作，但并未涉及加劲板动力稳定的研究。

鉴于目前加劲板动态屈曲的研究成果并不多见，且各种方法均存在一定的缺点，本文针对四边简支加劲板，提出了动态屈曲临界荷载的求解方法，运用Hamilton原理建立加劲板动态屈曲特征方程。分析中考虑初始几何缺陷的影响，并讨论了初始几何缺陷、加劲肋的数量及其刚度的变化对动态屈曲临界荷载的影响。研究结果也为加劲板的结构设计方法提供一定的参考。

1参数说明与控制方程的建立

1.1参数说明

1.2加劲板的位移函数及初始几何缺陷的考虑

考虑四边简支加劲板，则简谐振动板的横向位移函数可以表示为：

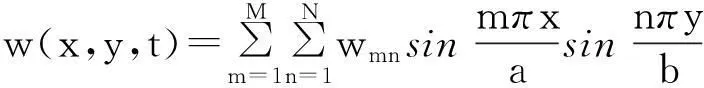
(1)

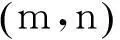
板件在加工及制作中，不可避免地存在误差导致板件出现各种面外的变形，这些面外变形称为初始几何缺陷。初始几何缺陷在加劲板的制作和安装过程中是无法避免和估计其大小的，初始几何缺陷的形状通常可以根据板的屈曲模态确定[18]：

(2)

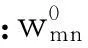
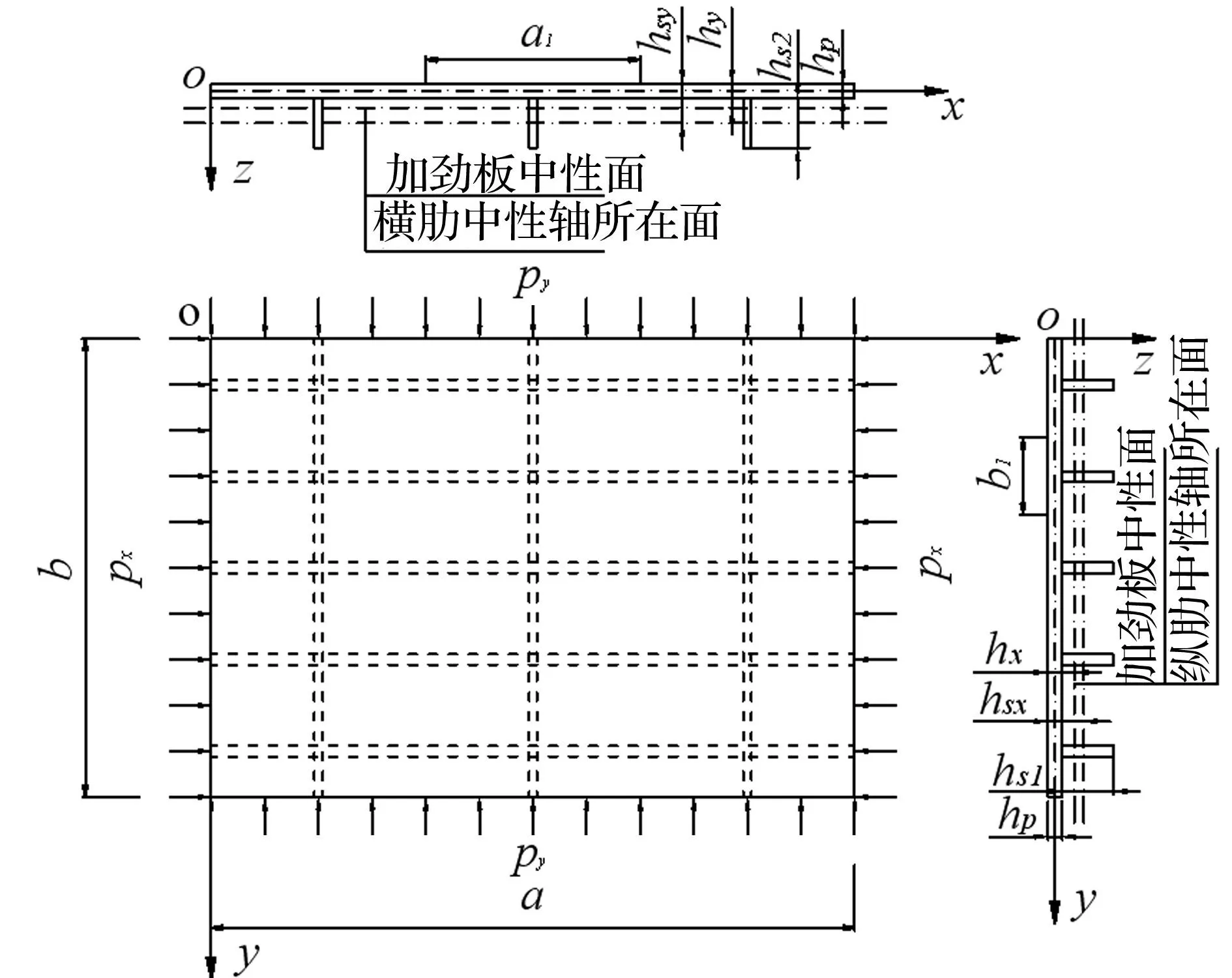
图1　加劲板计算示意图 Fig.1 Geometry of a stiffened plate

1.3控制方程的建立

分析中作以下两点假设：第一，将加劲肋视为Euler梁，同时考虑扭转效应；第二，母板按经典薄板理论计算。下面分别计算纵肋、横肋及母板的动能与应变能，并运用Hamilton原理建立加劲板动态屈曲特征方程。加劲肋的应变能包括拉压应变能、弯曲应变能与扭转应变能，母板的应变能包括弯曲应变能与膜应变能。为了得到加劲肋应变能中的拉压应变能以及母板应变能中的膜应变能，首先应确定纵肋、横肋中性轴及母板中性面x与y方向的应变，根据图1所示加劲板的几何参数经过简单的几何运算可以得到纵肋、横肋中性轴及母板中性面的应变分别为：

(3)

(4)

(5)

另外，母板中面应力与应变的关系为：

(6)

(7)

(8)

根据以上各式可以确定纵肋、横肋及母板的动能与应变能。

工程中通常不考虑面内惯性效应[18]，因此加劲板动能的计算只考虑横向运动的动能。第k条纵肋的动能与应变能分别为：

(9)

(10)

第k条横肋的动能与应变能分别为：

(11)

(12)

母板的动能与应变能分别为：

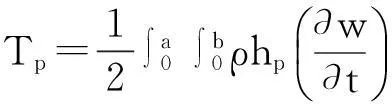
(13)

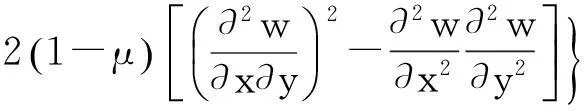
(14)

根据式(9)~式(14)可以得到加劲板总的动能与应变能分别为：

T=Tsx+Tsy+Tp

(15)

V=Vsx+Vsy+Vp

(16)

考虑加劲板沿x与y方向分别作用有均匀面内随从压力px与py，并且令：

py=λpx=λp

(17)

式中：λ为一常数，表示py与px的比例关系。

外力所做的功为：

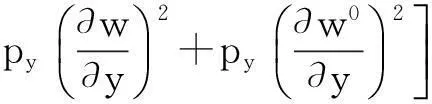
(18)

根据式(15)、(16)和(18)，并运用Hamilton原理可以得到关于加劲板动态屈曲的一组线性齐次方程组，用矩阵形式可表示为：

(19)

给定不同的p值，式(19)成为关于ω2的广义特征值问题。随着p增大，ω2可能出现两种情况：其一是ω2由正变负，使ω2=0时的p值为发散失稳临界荷载，简称发散荷载；其二为ω2由一对相邻的值彼此接近到相等，然后成为一对共轭复数，使一对相邻的ω2相等时的p值为颤振失稳临界荷载，简称颤振荷载。运用MATLAB编制相应的计算程序可以方便地实现这一计算过程。

2算例分析

2.1加劲板参数

选择如下参数对加劲板动态屈曲临界荷载进行讨论：ρ=7.85×103kg/m3、E=2.1×1011Pa、μ=0.3、G=8.1×1010Pa、a=1.5m、b=1.2m、hp=0.005m、hs1=hs2=0.09m、D=2.404×103N·m2/m、EAsx=EAsy=7.56×107N、λ=0.5。

2.2方法验证

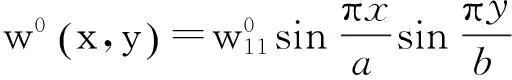
由表1可以看出，对于前两种加劲板，当级数项数取到7×7时，发散荷载已经收敛；对于第三种加劲板，当级数项数取到8×8时，发散荷载收敛。这说明只需选取8×8项级数即可满足计算要求。另外，文献[7]的有限元方法的计算结果与本文方法的计算结果比较接近，但均偏高，一方面验证了本文方法的正确性，另一方面是由于文献[7]中的有限元方法计算中未考虑初始几何缺陷的原因，而初始几何缺陷的存在会使得加劲板的临界荷载降低，因此本文的方法更具有实用性。

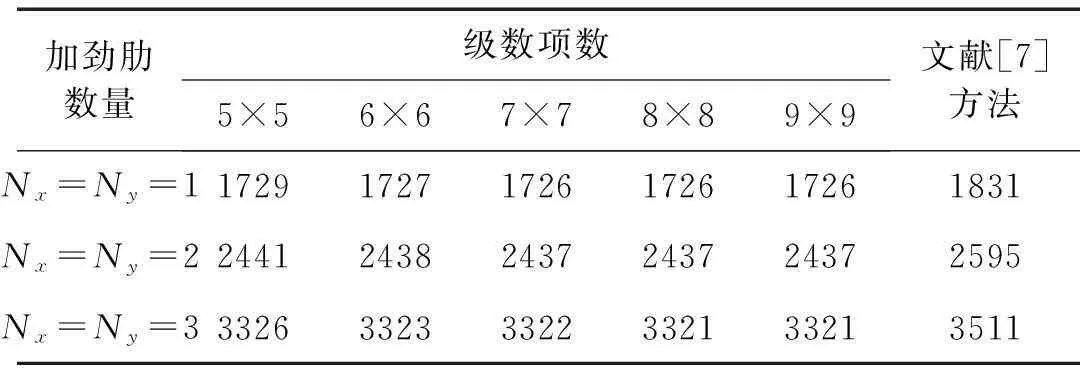
表1　四边简支加劲板的发散荷载(单位：kN/m)

2.3动态屈曲的影响因素分析

为了分析加劲板动态屈曲的影响因素，针对以下四种情况分别讨论初始几何缺陷、加劲肋的数量及其刚度的变化对动态屈曲临界荷载的影响：

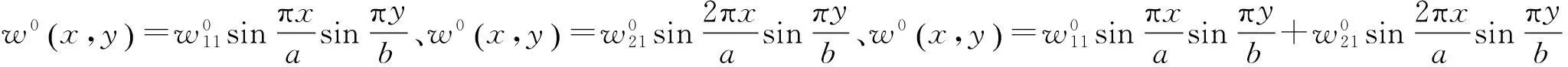
根据前面的分析结果，为了保证计算精度，以下计算中取M=N=8即可。根据以上三种情况计算得到的临界荷载同样是发散荷载，图2~图4分别是初始几何缺陷、加劲肋的数量及其刚度的变化对荷载-频率曲线的影响。

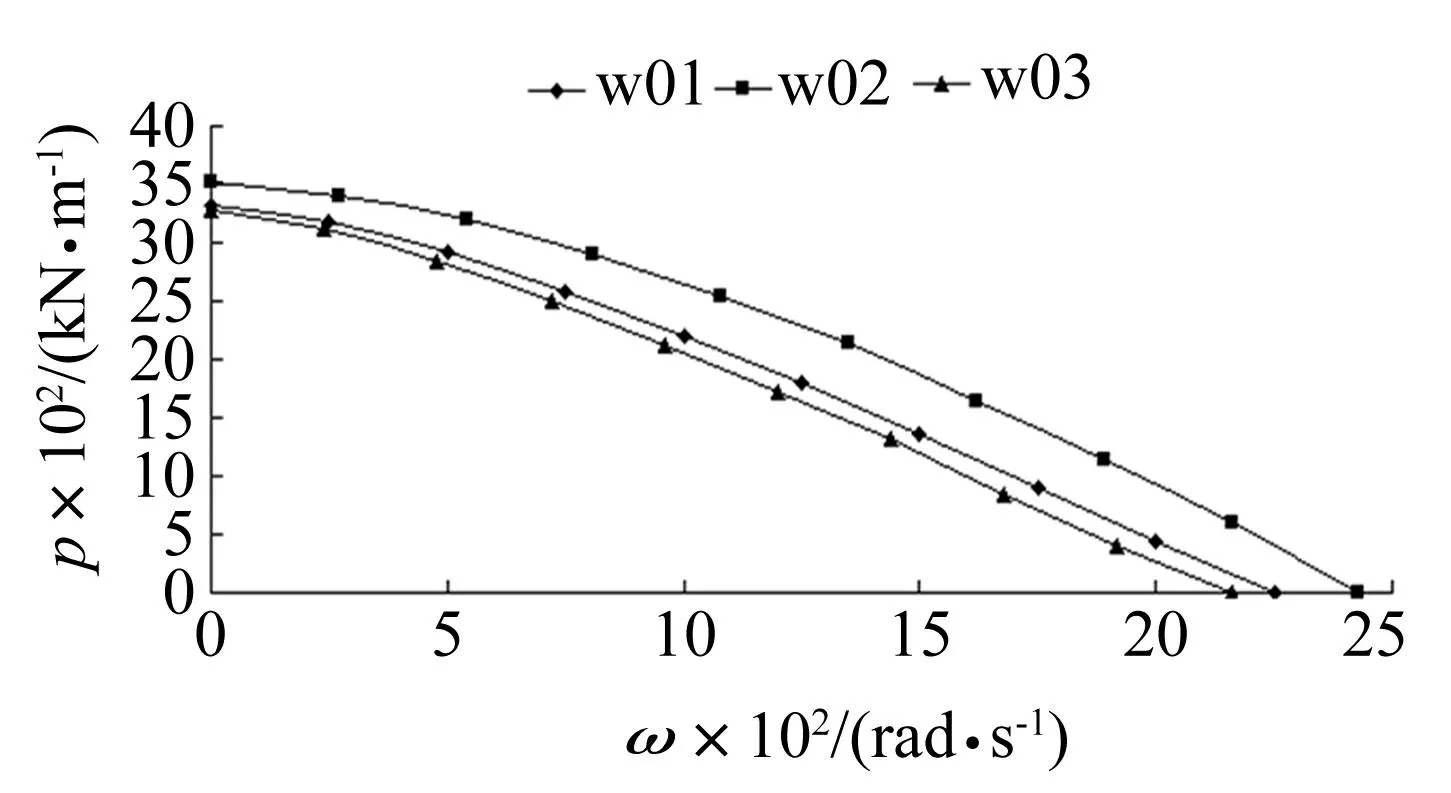
图2　初始几何缺陷的变化对荷载-频率曲线的影响 Fig.2 The influence on load-frequency curves of the initial geometrical imperfections

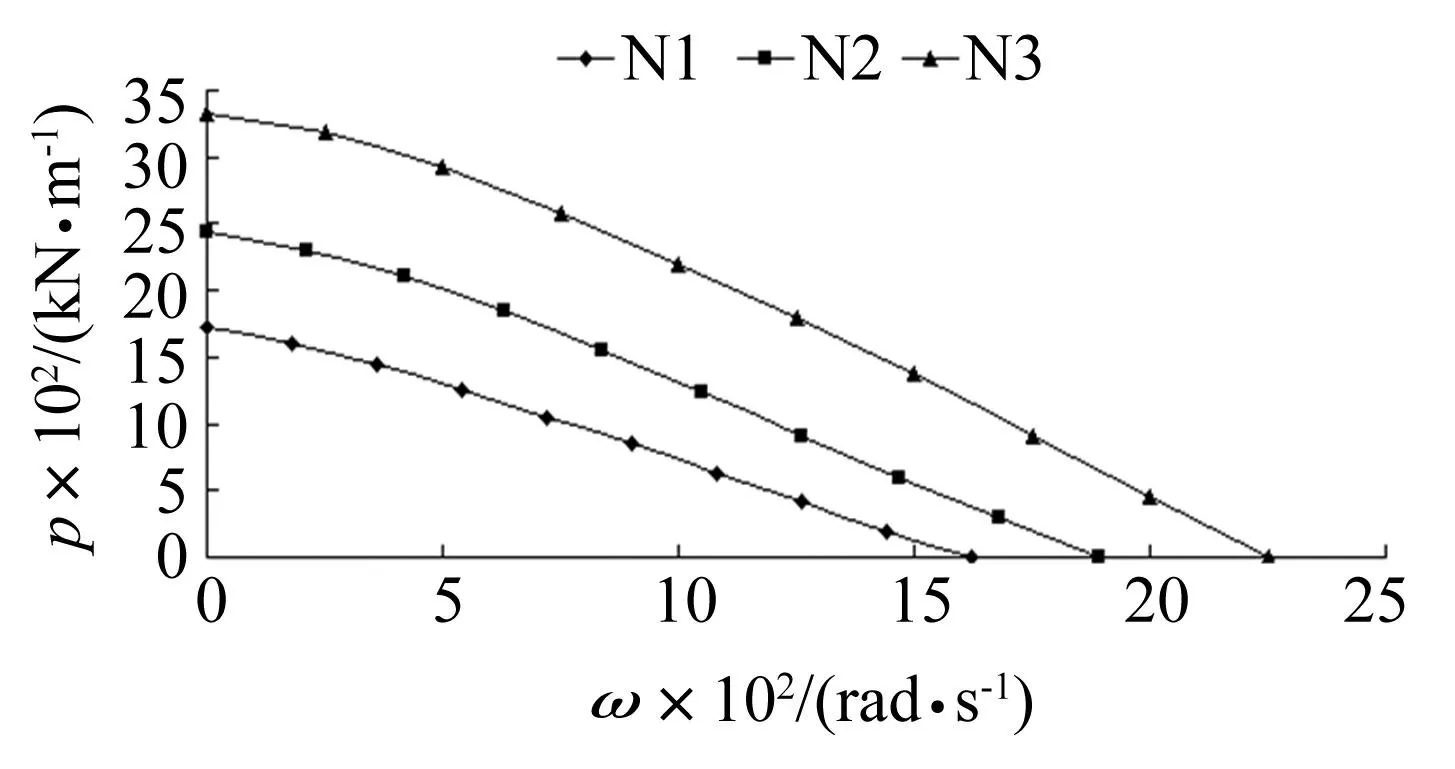
图3　加劲肋的数量的变化对荷载-频率曲线的影响 Fig.3 The influence on load-frequency curves of the numbers of stiffeners

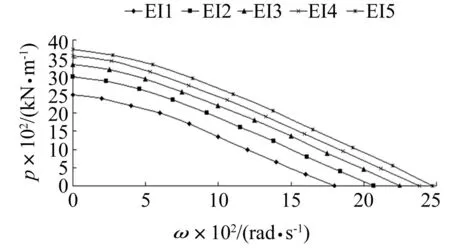
图4　加劲肋的抗弯刚度的变化对荷载-频率曲线的影响 Fig.4 The influence on load-frequency curves of the flexural rigidities of stiffeners

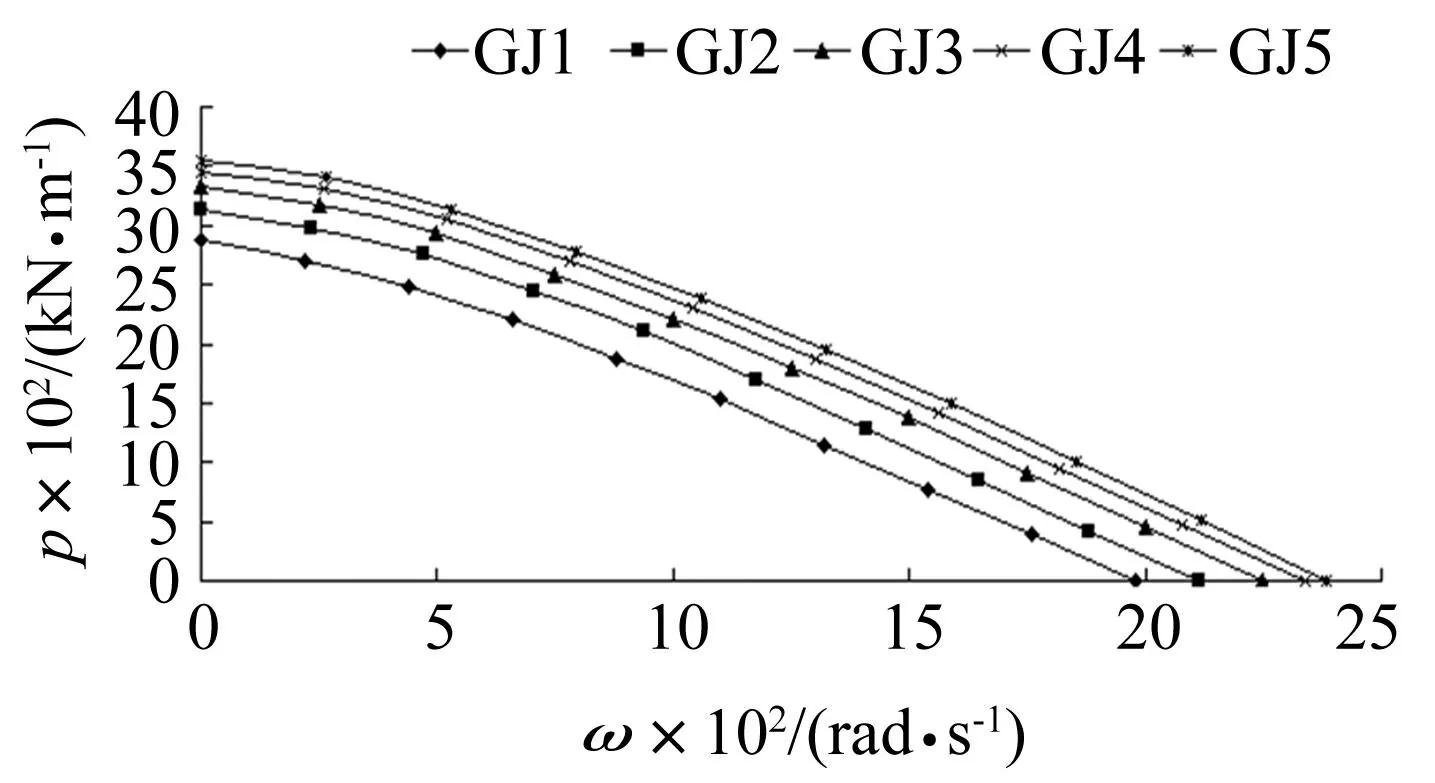
图5　加劲肋的扭转刚度的变化对荷载-频率曲线的影响 Fig.5 The influence on load-frequency curves of the torsional rigidities of stiffeners

图2给出了三种缺陷形式下，加劲板的荷载-频率曲线。可以看出，当初始缺陷形式含有一阶模态时，加劲板一阶模态在动态屈曲模态中绝对占优，且使得屈曲易于发生，也就是说，不含一阶模态的初始几何缺陷有利于提高加劲板抵抗动态屈曲的能力。

图3给出了三种不同数量加劲肋情况下，加劲板的荷载-频率曲线。可以看出，随着加劲肋数量的增加，加劲板的动态屈曲临界荷载迅速增加，另外可以发现，在x与y方向同时设置3个加劲肋的临界荷载大约是在两个方向同时设置1个加劲肋的2倍，这也进一步说明加劲肋的设置可以有效提高加劲板的抗动态屈曲能力。

图4给出了加劲肋抗弯刚度不同的五种情况下，加劲板的荷载-频率曲线。可以看出，当抗弯刚度由2.85×103N·m2增加到3×103N·m2时，加劲板的临界荷载的增幅大约500 kN/m，而当抗弯刚度由3.3×103N·m2增加到3.45×103N·m2时，加劲板的临界荷载的增幅大约只有200 kN/m，这说明随着加劲肋抗弯刚度的提高，加劲板的动态屈曲临界荷载亦随之增加，但是增幅逐渐变小。

图5给出了加劲肋扭转刚度不同的五种情况下，加劲板的荷载-频率曲线。可以看出，当扭转刚度由115 N·m2增加到130 N·m2时，加劲板的临界荷载的增幅大约250 kN/m，而当扭转刚度由160 N·m2增加到175 N·m2时，加劲板的临界荷载的增幅大约只有100 kN/m，这说明随着加劲肋扭转刚度的提高，加劲板的动态屈曲临界荷载亦随之增加，但是增幅逐渐变小。

3结论

本文运用Hamilton原理建立了具有初始几何缺陷加劲板动态屈曲的特征方程。选取一个数值算例，对四边简支加劲板的动态屈曲临界荷载进行分析，主要得到以下几点结论：

(1)本文方法的正确性通过文献[7]有限元方法的计算结果得到验证，同时由于考虑了初始几何缺陷，并且采用比较少的级数项数便可以收敛，因此本文的方法更具有实用性；

(2)对于本文的各种形式的四边简支加劲板，动态屈曲临界荷载均为发散荷载；

(3)一阶模态的初始几何缺陷对加劲板的临界荷载影响很大，而不含一阶模态的初始几何缺陷有利于提高加劲板抵抗动态屈曲的能力；

(4)增加加劲肋的数量可以显著提高加劲板的抗动态屈曲能力；

(5)随着加劲肋抗弯刚度的提高，加劲板的动态屈曲临界荷载亦随之增加，但是增幅逐渐变小。

(6)随着加劲肋扭转刚度的提高，加劲板的动态屈曲临界荷载亦随之增加，但是增幅逐渐变小。

参考文献

[1]Timoshenko S P, Gere J M.弹性稳定理论[M].张福范译.北京:科学出版社, 1965.

[2]Paik J K, Lee M S. A semi-analytical method for the elastic-plastic large deflection analysis of stiffened panels under combined biaxial compression/ tension, biaxial in-plane bending, edge shear, and lateral pressure loads [J]. Thin-Walled Structures, 2005, 43(3): 375-410.

[3]李立峰,邵旭东.正交异性闭口加劲板的承载力分析理论及试验研究[J].土木工程学报, 2007, 40(6): 42-48.

LI Li-feng, SHAO Xu-dong. Theoretical study and model test on the capacity of orthotropic U-rib stiffened plates [J]. China Civil Engineering Journal, 2007, 40(6): 42-48.

[4]狄谨.钢箱梁梯形肋加劲板受力性能与设计方法研究[D].西安:长安大学, 2009.

[5]Leipholz H, Pfendt F. Application of extended equations of galerkin to stability problems o f rectangular plates subjected to follower forces [ J] . Computer Methods in Applied Mechanics and Engineering, 1983, 37: 341-365.

[6]Srivastava A K L, Datta P K, Sheikh A H. Dynamic instability of stiffened plates subjected to non-uniform harmonic in-plane edge loading [J]. Journal of Sound and Vibration, 2003,262(5):1171-1189.

[7]Patel S N, Datta P K, Sheikh A H. Buckling and dynamic instability analysis of stiffened shell panels[J]. Thin-Walled Structures, 2006, 44(3): 321-333.

[8]张涛,刘土光,熊有伦,等.流固冲击下加筋板的非线性动态屈曲[J].应用数学和力学, 2004, 25(7): 755-762.

ZHANG Tao, LIU Tu-guang, XIONG You-lun, et al. Dynamic buckling of stiffened plates under fluid-solid impact load [J]. Applied Mathematics and Mechanics, 2004, 25(7): 755-762.

[9]Huang H W, Han Q. Nonlinear dynamic buckling of functionally graded cylindrical shells subjected to time-dependent axial load [J]. Composite Structures, 2010, 92(2): 593-598.

[10]Yang X D, Tang Y Q, Chen L Q, et al. Dynamic stability of axially accelerating Timoshenko beam: Averaging method [J]. European Journal of Mechanics A/Solids, 2010, 29(1): 81-90.

[11]Banichuk N, Jeronen J, Neittaanmaki P, et al. On the instability of an axially moving elastic plate [J]. International Journal of Solids and Structures, 2010, 47(1): 91-99.

[12]Chen W R. Dynamic stability of linear parametrically excited twisted Timoshenko beams under periodic axial loads [J]. Acta Mechanica, 2011, 216(1-4): 207-223.

[13]程昌钧,范晓军.粘弹性环形板的临界载荷及动力稳定性[J].力学学报, 2001, 33(3): 365-376.

CHENG Chang-jun, FAN Xiao-jun. Critical loads and the dynamical stability of viscoelastic annular plates [J]. Acta Mechanica Sinica, 2001, 33(3): 365-376.

[14]莫宵依,计伊周,王忠民.矩形薄板在非保守力作用下的动力稳定性[J].西安理工大学学报, 2000, 16(4): 370-375.

MO Xiao-yi, JI Yi-zhou, WANG Zhong-min. Dynamic stability of rectangular plates under the action of nonconservative forces [J]. Journal of Xi’an University of Technology, 2000, 16(4): 370-375.

[15]周银锋,王忠民,王砚.考虑随从力作用的运动粘弹性板的动力稳定性[J].工程力学, 2009, 26(1): 25-30.

ZHOU Yin-feng, WANG Zhong-min, WANG Yan.Dynamic stability of moving viscoelastic plate subjected to follower force [J]. Engineering Mechanics, 2009, 26(1): 25-30.

[16]韩大伟，王安稳.三边简支一边固支矩形薄板动力屈曲解析解[J].振动与冲击,2013,32(2):140-142.

HAN Da-wei,WANG An-wen.Analytical solution to dynamic buckling of a rectangular thin plate with one edge clamped and other three edges simply supported[J].Journal of Vibration and Shock,2013,32(2):140-142.

[17]邓磊,王安稳,毛柳伟.面内阶跃载荷下矩形薄板的塑性动力屈曲[J].固体力学学报,2013, 34(5):459-465.

DENG Lei, WANG An-wen, MAO Liu-wei. Plastic dynamic buckling of rectangular thin plates subject to in-plane step load[J]. Chinese Journal of Solid Mechanics, 2013, 34(5):459-465.

[18]Amabili M. Nonlinear vibrations and stability of shells and plates [M]. Cambridge: Cambridge University Press, 2008.

第一作者严波男，博士，教授，博士生导师，1965年5月生