非对称周期结构中耦合波的传播特性

非对称周期结构中耦合波的传播特性

陈荣,吴天行

(上海交通大学机械系统与振动国家重点实验室,上海200240)

摘要：为了揭示周期结构中纵向波和弯曲波的耦合作用，设计了对称和非对称周期结构。考虑子结构中的纵向和弯曲耦合运动，利用导纳法和传递矩阵法，得到了周期单元的传递方程。由于结构中存在多种波的耦合作用，在求解周期单元的传播系数时将出现变态矩阵，采用波型分组法，求得了周期结构中多种波型的传播系数。推导了半无限长和有限长周期结构在纵向力、横向力和弯矩作用下的动态响应。数值计算结果表明，对称周期结构中纵向波和弯曲波的带隙结构相互独立；非对称周期结构中纵向波和弯曲波的耦合明显改变了两种波的带隙结构，只有在两种波阻带重叠的频段内结构上的振动响应才存在衰减。

关键词：周期结构；传递矩阵法；Euler梁；耦合波；传播系数

中图分类号:TB115;TH113;O321文献标志码：A

基金项目：国家自然科学基金资助项目(51079118,51279148);武汉理工大学自主创新研究基金资助(135105006)

收稿日期：2014-05-12修改稿收到日期：2014-07-30

基金项目：国家自然科学基金资助(11072066);国家重点基础研究发展计划(973)：(2013CB733004)

收稿日期：2013-05-28修改稿收到日期：2014-02-11

Coupledwavepropagationinasymmetricperiodicstructures

CHEN Rong, WU Tian-xing(StateKeyLaboratoryofMechanicalSystemandVibration,ShanghaiJiaotongUniversity,Shanghai200240,China)

Abstract:Symmetric and asymmetric periodic structures were designed to investigate the coupling of longitudinal and flexural waves propagating in the structures. By use of mechanical mobility method and transfer matrix method, transfer matrices of the elements were derived in the consideration of the coupling of longitudinal and flexural wave motions. The multiple types of waves propagating in the periodic structures were divided into two categories to avoid the numerical difficulties in solving the case of ill-conditioned transfer matrix. The propagation constants of the longitudinal and flexural waves were calculated, and the harmonic responses of semi-infinite and finite periodic structure in symmetric and asymmetric arrangements were obtained. Numerical simulations reveal that longitudinal wave and flexural wave are uncoupled in symmetric periodic structure; the band structures of longitudinal and flexural wave are significantly influenced by the coupling of the two waves, and longitudinal and flexural vibration response are attenuated only in the zones where stop bands of the both waves overlap.

Keywords:periodicstructure;transfermatrixmethod;eulerbeam;couplingwave;propagationconstant

在实际工程中，许多结构如磁悬浮列车的承载导轨、多跨距桥梁、船舶结构、 钢筋混凝土都是由一定数量相同或类似的单元结构，以相同方式连接而成的，他们具有振动带隙特性。当一种弹性波在一维对称周期结构中传播时，某些频率范围内波不能通过，称之为带隙(bandgap)；而某些频率范围内波可以自由传播，称之为通带(passband)。对于非对称周期结构，多种波在结构中传递和反射之后可能会引起相互干涉、耦合，而不同波型的耦合作用会改变结构中原有单一波型的振动带隙，进而影响周期结构的振动传递衰减性能。因此有必要对非对称周期结构中不同波的耦合振动带隙进行研究。

从20世纪60年代开始，各国对周期结构的振动特性给予了更多的关注，并进行了比较深入的理论和实验研究，研究对象主要集中在实际工程中广泛应用的周期结构，如周期支撑，周期梁、板和壳体，以及周期桁架结构等。而对复杂周期结构中多种波耦合的研究的文献则相对较少。早在半个世纪以前，Muller[1]把钢筋混凝土地板简化成带偏心子结构梁，研究了梁结构中耦合波的传播特性。Mead[2]采用动柔度法研究了一维周期结构中波的传播，之后他利用单元传递方程的特征向量提取正则力向量和位移向量[3]，计算了半无限长周期结构的耦合振动响应，并解释了带偏心谐振器的周期简支梁中纵向-弯曲波的相互耦合、转换现象[4]。Heckl[5]建立了周期简支Timoshenko梁的力学模型，研究了周期梁中纵向波、弯曲波、剪切波和扭转波的耦合特性，并给出了不同波的传播系数。Roy等[6]采用传递矩阵法，研究了带对称/非对称柔性筋的周期梁中的弯曲波的衰减特性。近期，Friss等[7-8]针对一种带非对称分支结构的周期梁，研究了半无限长周期梁中纵向-弯曲耦合波的传播特性，并实验验证了有限长周期梁的振动响应。Yi等[9]采用传递矩阵法计算了周期单元中耦合波的传播系数，发现在结构中传播的三种对称波和三对反对称波相互耦合。黄修长等[10-11]研究周期结构中波传播特性的对象主要集中在一维结构，即结构中只存在单一波型的情形，而对非对称周期结构中耦合波传播特性的研究还相对缺乏。

本文分析了非对称周期结构中纵向-弯曲耦合波的传播特性，并与对称周期结构中波传播进行了比较，揭示了耦合作用对结构中波传播系数和对半无限长和有限长周期结构振动响应的影响。这一研究工作将为非对称梁类结构中求解耦合波传播系数提供一种有效方法，并为非对称梁类结构的减振设计提供参考依据。

1模型描述

如图1(a)和(b)所示分别为由横向梁和竖向梁交替排列组成的半无限长对称周期结构和非对称周期结构模型。施加在结构端部的激振力向量FIeiωt包含沿着x方向的纵向力(fIx)、沿着y方向的横向力(fIy)以及绕着z轴的弯矩(MIz)。因此结构的响应具有三自由度，包括纵向速度、横向速度和转角速度。当施加激振力时，非对称结构上的响应由纵向波和弯曲波共同引起。而为了更好地理解结构中弯曲波和纵向波的耦合效果，有必要分析纵向波和弯曲波互不耦合的结构(即对称周期结构)的波传播特性。对称/非对称结构的周期单元如图1(c)所示。为了减少传播系数的个数，我们在沿着y轴中心的横梁上分割，这样选取的周期单元只有一个输入端一个输出端，相应地所要求解的传播系数的个数较少。

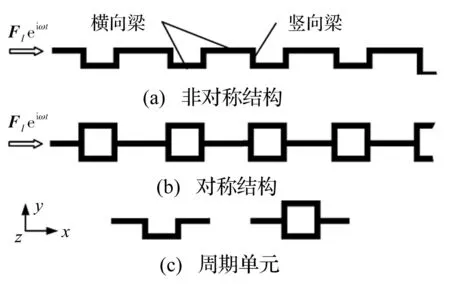
图1　周期结构模型 Fig.1 Model of periodic structure

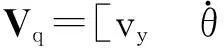
2力学模型

2.1子结构振动导纳方程

如图2所示为对称/非对称结构周期单元的振动传递路径以及各子结构端部振动量Ux的标识，其中Uq=[VqFq]T(下标q表示I、11、12、21、22、31、32、41、42或O)，Vq为端部的速度向量，Fq为端部的力向量。将如图2中所示各子结构模型化为一具有密度ρ，以损耗因子η描述结构阻尼的Euler梁和一等截面杆的组合模型，综合两端自由杆的纵向振动导纳和两端自由Euler梁的弯曲振动导纳，得到各子结构的振动导纳方程[12]，写成传递方程形式

U11=TAUI，U21=TBU12，U31=TCU22，

U42=TDU32，UO=TEU41

(1)

其中:Ty表示梁y的振动传递矩阵(下标y表示A、B、C、D或E)。各子结构连接界面处连续性条件，可知界面力和速度存在如下关系

Uz2=CUz1

(2)

其中C=(I0;0 -I)，I为单位矩阵，0表示零矩阵，下标z=1, 2, 3, 4。

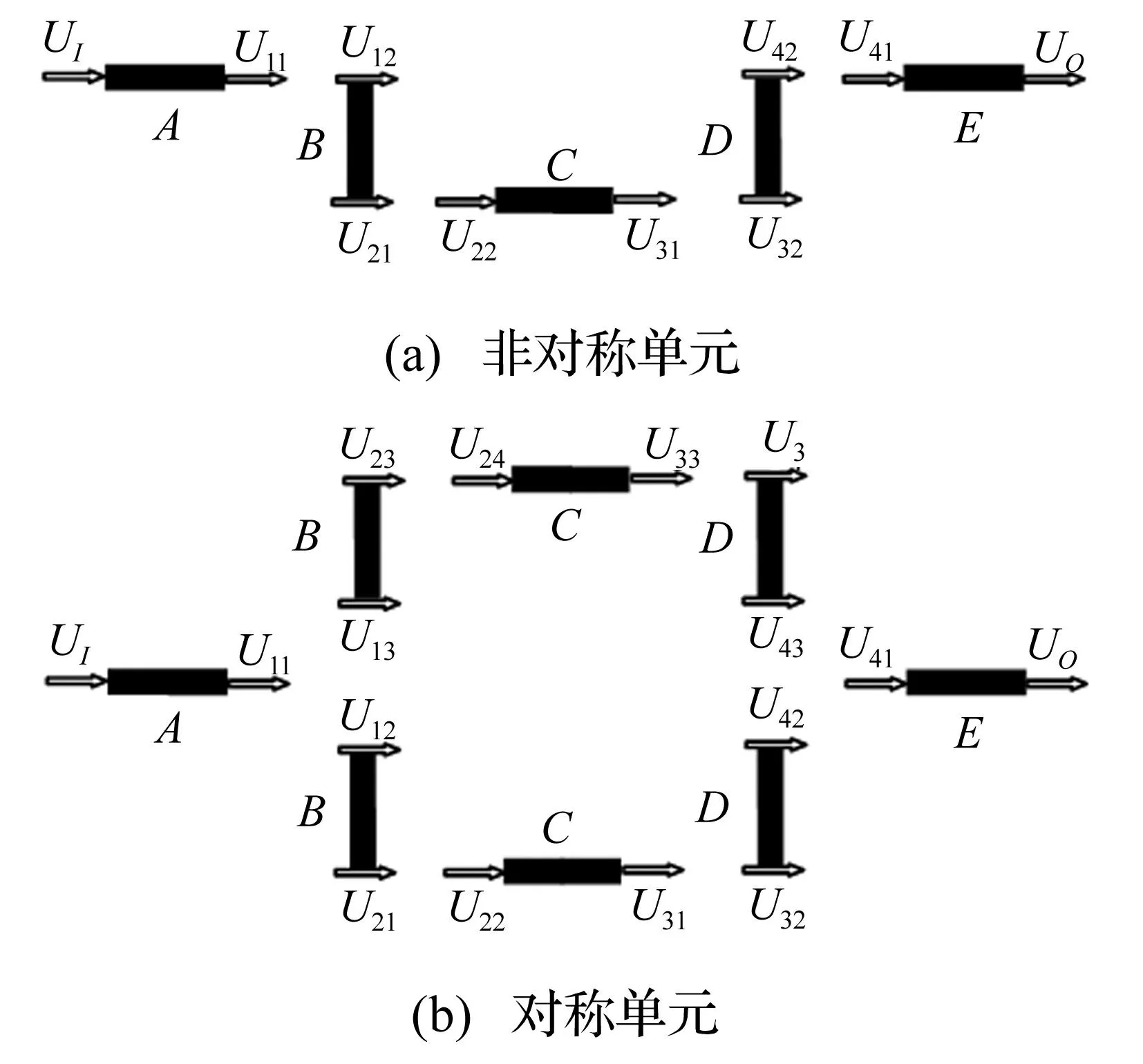
图2　振动传递路径 Fig. 2 Vibration transmission path

周期单元的振动传递方程可以写成如下形式

UO=Ta(s)UI

(3)

依据传递矩阵法，综合式(1)~式(6)可以求得非对称结构周期单元的传递矩阵Ta=TECTDCTCCTBCTA。同理可以求得如图2(b)所示对称结构的传递矩阵Ts=TECUCTA，其中

式中:M=Mt+Mb，Tt=TBCTCCTD，Tb=TDCTCCTB，Xij为矩阵X的第3i-2行至(3i)行第3j-2列至3j列子矩阵，i, j=1, 2，这里矩阵X表示矩阵M、Tt或Tb。

把对称/非对称周期单元的传递方程式(7)写成导纳方程的形式

(4)

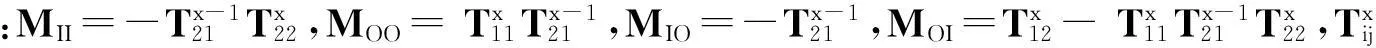
2.2传播系数

当一种波通过周期结构时，由周期单元端部的速度连续性和力平衡性，可知速度向量VI、VO和力向量FI、FO存在如下关系[4]

VO=eμVI，FO=-eμFI

(5)

综合式(4)和式(5)，可得周期单元端部的速度向量与力向量的关系

VI=(MII-eμMIO)FI

(6)

代入式(4)并消去VI可得方程

(MII+MOO-eμMIO-e-μMOI)FI=0

(7)

表示为特征值问题，式(7)可以写成

(8)

基于第一节中对速度和力的分类，把周期单元输入/输出端的速度和力向量分块

同样地，依据类型1和类型2坐标把周期单元的子导纳矩阵分块，并且由于单元的对称性，子导纳矩阵存在如下关系

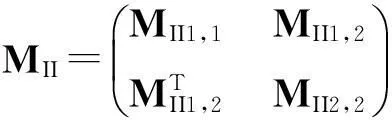
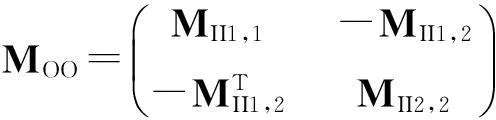
(9)

其中:子矩阵MII1,1，MII2,2，MIO1,1和MIO2,2都为对称矩阵。把欧拉公式eμ=(sinhμ+coshμ)/2以及式(13)分别代入式(11)和(12)可得

(10)

(12)

由式(9)或(12)可以求得3对传播系数，即横向运动，转角运动和纵向运动对应的波型的传播系数。

2.3半无限长周期结构的动态响应

激振力F0施加在半无限长周期结构的端部时，结构中存在三种正向传播波，对于非对称周期结构三种波都影响结构的振动响应，而对于对称周期结构，结构的纵向运动只受纵向波的影响而弯曲运动只受弯曲波的影响。利用波动理论可得到半无限长结构激励点和传递到第q个周期单元右端的速度响应分别为[7]

(12)

(13)

其中e-qμ表示包含所有e-qμi的对角矩阵，i =1,2,3，f+为3个正向传播波的正则化力向量所组成的3×3矩阵，它通过把3个正向传递波的传播系数-μi依次代入式(11)求得的3个正则力向量叠加而成。

2.4有限长周期结构动态响应

对于半无限长周期结构，不考虑边界波的反射作用，而工程实际中的周期结构往往是由有限周期单元组成的，因此有必要考虑结构的边界反射研究有限长周期结构的动态响应。对于包含N个周期单元的两端自由对称/非对称周期结构，把结构在激励点处分成两个子结构，分别记为m-子结构和(N-m)-子结构，利用波动理论可得到周期结构在第q个周期单元左端的振动响应方程[8]

Vq=MqmFm

(14)

其中:Mqm=δqm(I+γmm-1δmm)-1为周期结构的导纳矩阵δqm=(ζ+e-(q-m))μ+ζ-e(q-m)μe-(N-m)μrBe-(N-m)μ)(f++f-e-(N-m)μrBe-(N-m)μ)-1，γmm=(ζ+e-mμrA+ζ-e-mμ)(-f+e-mμrA-f-e-mμ)-1,δmm可以通过把矩阵δqm中的q替换成m得到， I 为三阶单位矩阵,rA=f+-1f-和rB=f--1f+为结构边界的反射矩阵，ζ+=MIIf+-MIOf+e-μ，ζ-=MIIf--MIOf-eμ。

3数值分析及讨论

下面给出了对称/非对称周期结构的数值分析，为了简便起见，我们把所有子结构取相同的物理参数，即所有子结构的材料均为铝，其密度ρ为2 700kg/m3，弹性模量E为7.8×1010N/m2，结构阻尼通过取复弹性模量实现，即E*=E(1+iη)，η=0.001为结构阻尼比。如图1(c)所示周期单元中，所有沿着x方向的横向梁尺寸相同，长度、宽度和厚度分别为0.1m、0.02m和0.01m，所有沿着y方向的竖向梁尺寸相同，长度、宽度和厚度分别为0.05m、0.02m和0.005m。矩阵计算和数值分析在Matlab7.0中完成。

3.1传播系数

研究表明[7]对称周期结构中不存在纵向-弯曲耦合波，也就是纵向激振力不会引起弯曲波，而横向力或弯矩不会激起纵向波。如图3所示为对称周期结构中三类波型传播系数的衰减系数和相位系数的频变曲线。由于近场弯曲波的相位系数特征比较简单，为了简洁起见图中省略了该系数。纵向波依次在936~1 043Hz，1 522~2 757Hz和大于2 820Hz等频段出现阻带，即在这些频段内波不能传播。衰减系数越大，表征阻带内波经过相同周期数的传播后衰减幅度也越大。在其他频率范围，纵向波将毫无衰减地传递，称为通带。在通带范围内，纵向波传播系数的虚部近似地呈线性递增或递减，两个相邻阻带，波的相位相差π。阻带的频率位置和带宽则取决于结构的几何和材料属性。弯曲运动则由两个波型控制，其中一种波型的传播系数具有很高的衰减系数，在所研究的频率范围内都为阻带，称之为近场波[7]，与非对称结构中的近场弯曲波所不同的是，本文所研究对称结构中近场波在636~892Hz频段与弯曲波的衰减系数相同。另外一种弯曲波则由通带和阻带构成。弯曲波在结构中传播与否取决于这两种弯曲波型阻带的叠加，即只有在164~194Hz，403~896Hz，936~1 075Hz，1 228-2 890Hz，3 057~3 710Hz和大于3 834Hz的频段内，结构中的横向运动和转动才是被完全禁止的。

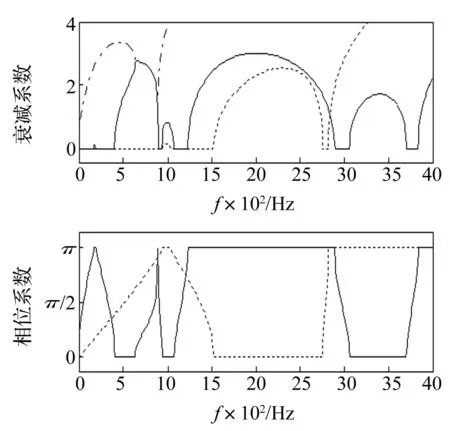
——为弯曲波，—-为近场弯曲波，---为纵向波 图3　对称结构中三类波型传播系数 Fig.3 Propagation constants in symmetry periodic structure

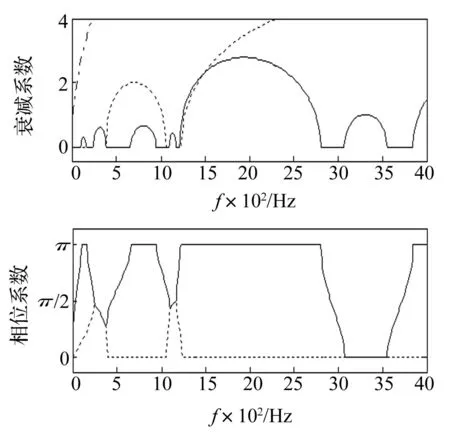
——为弯曲波，—-为近场弯曲波，---为纵向波 图4　非对称结构中三类波型传播系数 Fig. 4 Propagation constants in asymmetry periodic structure

如图4所示为非对称周期结构的传播系数的衰减系数和相位系数频变曲线。由于纵向-弯曲波的耦合作用，三种波型对结构的纵向、横向和弯曲运动都有贡献。非对称周期结构中也存在一个衰减系数很大的近场弯曲波，且该系数远大于如图3所示结果，因此非对称周期结构中的近场弯曲波衰减速度更快。如图3所示的纵向波和弯曲波的相位曲线都是以点的方式相交，并且相交后并不影响各自相位的变化趋势。而在图4中，相位曲线相交处，即在234~380Hz和1 093~1 164Hz频段出现重叠。纵向波的相位经过这些频段后，变成原来弯曲波的相位，而弯曲波的相位变成纵向波的相位，这表明在该频段出现了波型的强耦合或波型转换。在强耦合频段纵向波和弯曲波在结构中不能传播，属于阻带。另外660~949Hz，1 214~2 804Hz，3 070~3 555Hz和大于3 848Hz等频段,无论纵向波和弯曲波都不能传递，也属于阻带,而103~155Hz，384~660Hz, 949~1 060Hz，2 804~3 070Hz和3 555~3 848Hz等频段,纵向波和弯曲波中总有一种波型被禁止而另一种波型可以自由传播,属于通带，这一点也可以由下一节中结构的振动响应得到验证。

3.2半无限长周期结构

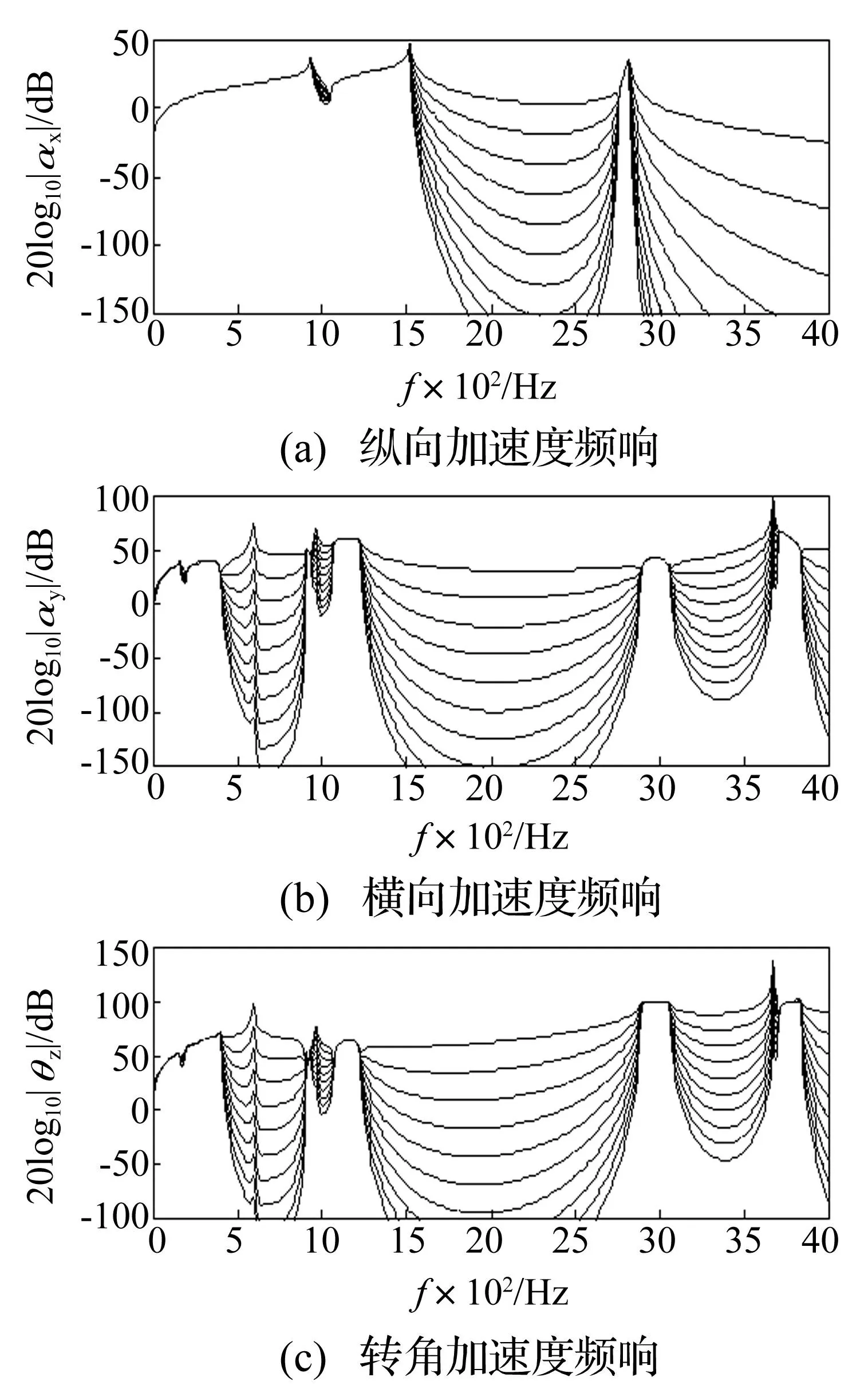
图5　复杂力作用下，对称结构上纵向(上图)、 横向(中图)和转角(下图)加速度频响 Fig.5 Longitudinal, transverse and angular acceleration responses on symmetry structure excited by a complex force

下面我们分析波型耦合对半无限长周期结构振动响应的影响。以在结构端部施加复杂简谐激振力F0=(1 1 1)T为例，比较无限长对称/非对称周期结构的振动响应的区别。如图5所示为对称周期结构上距离激励端前十个周期单元处的加速度频响，其中ax，ay和θz分别表示纵向，横向和转角加速度，加速度频响以分贝的形式表示。图5上图为纵向加速度频响，它在如图3所示纵向波的阻带频段出现明显的振动衰减现象，衰减幅度的大小与振动通过的周期数目成正比。图5的中、下图所示的横向和转角加速度频响在弯曲波的阻带频段出现明显的振动衰减现象。由此可见，在结构中纵向波和弯曲波共同存在的情形下，纵向振动响应不受弯曲波的影响，而弯曲振动响应也不受纵向波的影响，这也验证了对称周期结构中不存在纵向波和弯曲的耦合。另外，如图5所示，在纵向波和弯曲的通带，结构上无论经过多少个周期单元，其上振动响应毫无衰减。

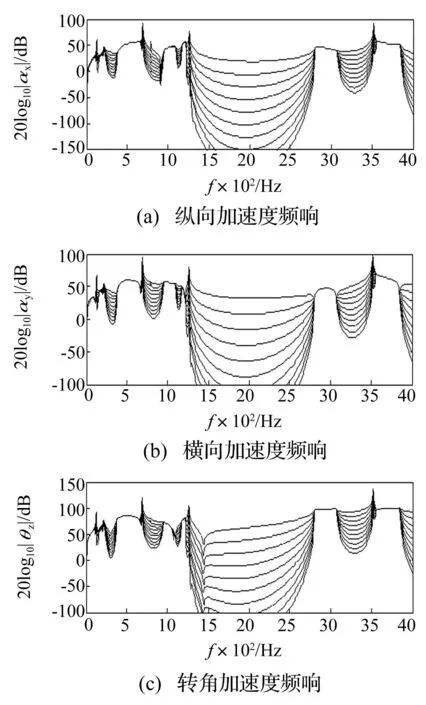
图6　复杂力作用下，非对称结构上 纵向、横向和转角加速度频响 Fig.6 Longitudinal, transverse and angular acceleration responses on asymmetry structure excited by a complex force

如图6所示为非对称周期结构上距离激振端前十个周期单元处的加速度频响，它们是由结构中纵向和弯曲波的耦合的作用结果。其中上图为纵向加速度频响，中图和下图所示分别为横向和转角加速度频响。与对称周期结构振动响应最明显的区别就是非对称周期结构的纵向和弯曲振动响应的衰减区域相同，而这些区域刚好与如图4所示阻带，即纵向波和弯曲波都不能在结构中传播的频率范围一致，其衰减幅度的大小与振动通过的周期数目成正比。而在通带无论经过多少个周期单元，结构上的纵向和弯曲振动响应无衰减。

3.3有限长周期结构

无限长周期结构仅考虑结构上的入射波(即正向传播波)，而工程实际中的结构都是有限长度的，不能忽略其边界的反射波(即负向传播波)。下面计算含10个周期单元的有限长对称/非对称周期结构在复杂激振力作用下的振动响应。对称周期结构两端自由，激振力作用于结构端部，分析结构上激励点以及距离激励点2个单元、4个单元和8个单元处的纵向加速度、横向加速度和转角加速度响应，结果分别如图7中上图、中图和下图所示。与无限长对称周期结构的振动响应相同点之处为，有限长周期结构上的纵向振动在纵向波阻带出现衰减，弯曲振动也在弯曲波阻带出现衰减，只是衰减幅度稍微变小。不同之处为，在波型通带，无限长周期结构中不同位置的振动响应相同，且曲线平滑无波峰；而有限长周期结构加速度频响曲线出现很多峰值，发现在每个通带，曲线上存在10个峰值，这一数值与结构中的周期数目是相等的，峰值所在的频率与两端自由周期结构固有频率一一对应。

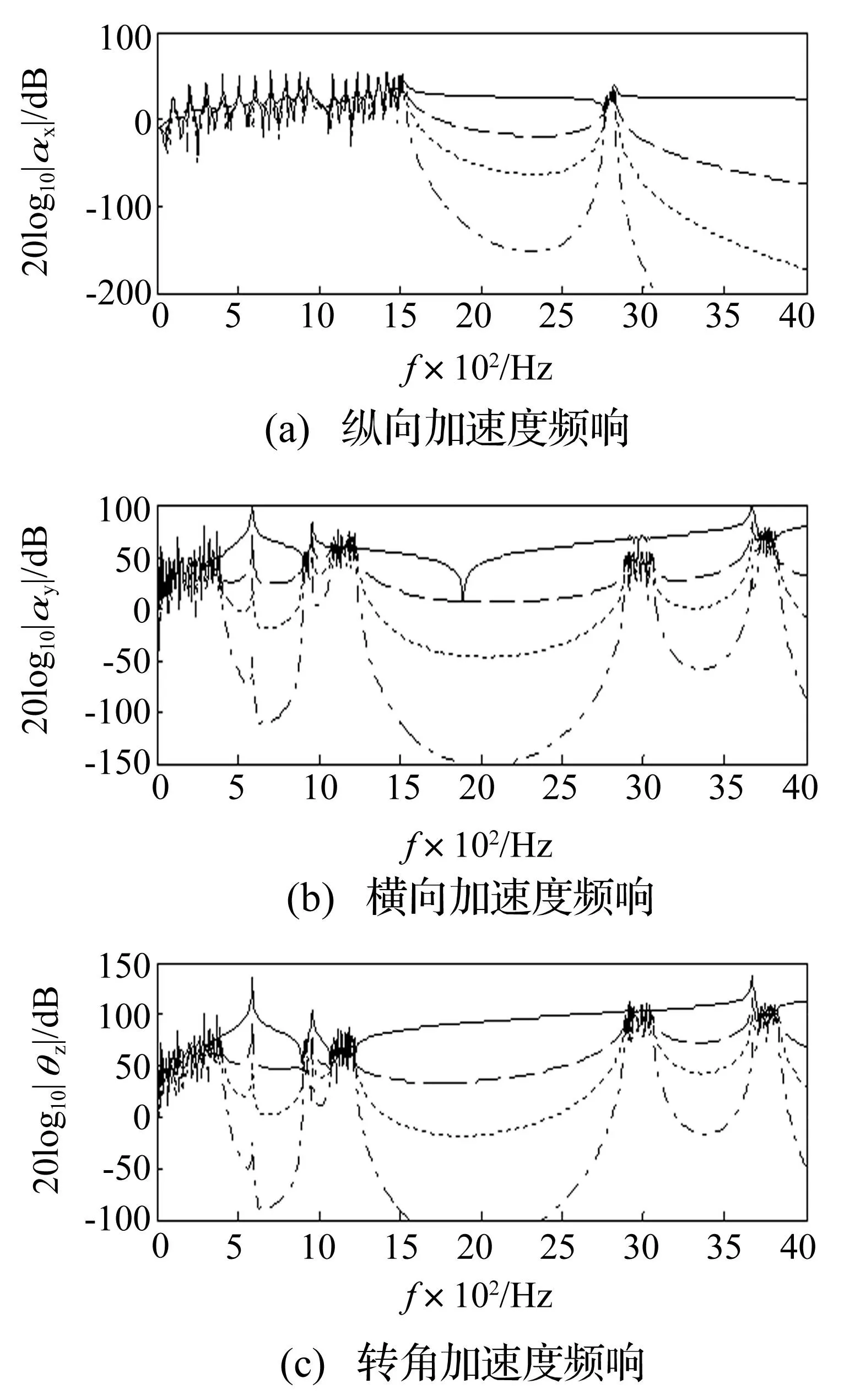
——　激振点，— —距离2个单元， ---距离4个单元， — - —距离8个单元 图7　复杂力作用下，对称结构上纵向(上图)、 横向(中图)和转角(下图)加速度频响 Fig.7 Longitudinal, transverse and angular acceleration responses on symmetry structure excited by a complex force

如图8所示为两端自由非对称周期结构上的纵向加速度、横向加速度和转角加速度响应。其中实线、虚线、点线和点划线分别为激励点以及距离激励点分别2个单元、4个单元和8个单元处的加速度频响曲线。与无限长非对称周期结构的振动响应相同点之处为，有限长周期结构上的纵向振动和弯曲振动也在纵向-弯曲耦合波阻带出现衰减。不同之处为，有限长周期结构加速度频响曲线出现很多峰值，在每个通带，曲线上存在10个峰值，峰值所在的频率与两端自由周期结构固有频率一一对应。

——激振点，— —距离2个单元， ---距离4个单元， — - —距离8个单元 图8　复杂力作用下，非对称结构上纵向、横向和转角加速度频响 Fig.8 Longitudinal, transverse and angular acceleration responses on asymmetry structure excited by a complex force

4结论

本文设计了对称和非对称周期结构，求解了周期结构中纵向和弯曲波的传播系数，推导了半无限长和有限长周期结构在复杂简谐力作用下的动态响应。数值研究结果表明：对称周期结构中纵向波和弯曲波的带隙结构相互独立，纵向波的阻带决定结构纵向振动响应的衰减频段，而弯曲波的阻带决定弯曲振动响应的衰减频段；非对称周期结构中纵向波和弯曲波的耦合明显改变了两种波的带隙结构，只有在两种波阻带重叠的频段结构上的振动响应才有衰减，纵向和弯曲振动响应衰减的频段相同。本文的研究工作为非对称梁类结构中求解耦合波传播系数提供了一种有效方法，并为非对称梁类结构的减振提供参考依据。

参考文献

[1]MüllerHL.Biegewellen-Dämmungansymmetrischenundexzentrischensperrmassen[D].Berlin:TechnischenUniversitätBerlin, 1957.

MüllerHL,Attenuationofbendingwavescausedbysymmetricalandeccentricblockingmasses[D].Berlin:TechnicalUniversityBerlin, 1957.

[2]MeadDJ.Wavepropagationandnaturalmodesinperiodicsystems:I.Mono-coupledsystems[J].JournalofSoundandVibration, 1975, 40(1):1-18.

[3]MeadDJ.Wavepropagationandnaturalmodesinperiodicsystems:II.Multi-coupledsystems,withandwithoutdamping[J].JournalofSoundandVibration, 1975, 40(1): 19-39.

[4]MeadDJ,MarkusS.Coupledflexural-longitudinalwavemotioninaperiodicbeam[J].JournalofSoundandVibration, 1983, 90(1): 1-24.

[5]HecklMA.CoupledwavesonaperiodicallysupportedTimoshenkobeam[J]JournalofSoundandVibration, 2002, 252(5): 849-882.

[6]RoyAK,PlunkettR.Waveattenuationinperiodicstructures[J].JournalofSoundandVibration, 1986, 104(3): 395-410.

[7]FriisL,OhlrichM.Couplingofflexuralandlongitudinalwavemotioninaperiodicstructurewithasymmetricallyarrangedtransversebeams[J].J.Acoust.Soc.Am., 2005, 118(5): 3010-3020.

[8]FriisL,OhlrichM.Coupledflexural-longitudinalwavemotioninafiniteperiodicstructurewithasymmetricallyarrangedtransversebeams[J].J.Acoust.Soc.Am., 2005, 118(6): 3607-3618.

[9]YiY,CheukMM,Astudyofcoupledflexural-longitudinalwavemotioninaperiodicdual-beamstructurewithtransverseconnection[J].J.Acoust.Soc.Am., 2009, 126(1): 114-121.

[10]黄修长，徐时吟，蒋爱华,等. 曲梁周期结构隔振器特性研究[J]. 振动与冲击，2012，31(5)：171-175.

HUANGXiu-chang,XUShi-yin,JIANGAi-hua,etal.Dynamicpropertiesofaperiodiccurved-beamstructureisolator[J].JournalofVibrationandShock, 2012, 31(5):171-175.

[11]王刚，温激鸿，刘耀宗,等. 一维粘弹材料周期结构的振动带隙研究[J]. 机械工程学报，2012，40(7)：47-50.

WANGGang,WENJi-hong,LIUYao-zong,etal.Researchonthevibrationbandgapsofonedimensionalviscoelasticperiodicstructure[J].ChineseJournalofMechanicalEngineering, 2012, 40(7):47-50.

[12]FrankF,JohnW.Advancedapplicationsinacoustics,noiseandvibration[M].Florida:CRCPress, 2004.

第一作者夏雪宝男，博士生，1989年1月生

通信作者向阳女，教授,博士生导师，1962年10月生

邮箱：yxiang@whut.edu.cn

第一作者潘冬男，博士，1984年5月生

邮箱：pandonghit@163.com