反常二重积分收敛性的判定

反常二重积分收敛性的判定

刘继成，王湘君

(华中科技大学 数学与统计学院，武汉 430074)

[摘要]华东师范大学数学系编《数学分析(下册)》教材在第21.8节介绍了反常二重积分收敛的定义、判定定理，作者发现教材中对本节内容的处理不够清晰，特别是没有给出定理21.19关于反常二重积分收敛等价于绝对收敛的直观解释.本文优化了该节的内容，理顺了反常二重积分收敛的判定方法，证明了无界区域上的二重积分转化为累次积分的定理，构造例子说明了反常一重积分收敛与反常二重积分收敛的本质区别.通过分析例子表明，在本文框架下判定反常二重积分收敛性及计算积分值是非常有效的.

[关键词]反常二重积分； 绝对收敛； 无界区域

[收稿日期]2015-03-24

[基金项目]华中科技大学自主创新研究基金(2014TS066)

[中图分类号]O172.2[文献标识码]C

通讯作者注王湘君为.

1反常二重积分收敛的定义

首先叙述无界区域上的反常二重积分收敛的定义，参见文献[1]P.279.

定义1设f(x,y)为定义在无界区域D上的二元函数.若对于平面上任一包围原点的光滑封闭曲线γ，f(x,y)在曲线γ所围的有界区域Eγ与D的交集Eγ∩D=Dγ上恒可积.令

若极限

存在有限，且与γ的取法无关，则称f(x,y)在D上的反常二重积分收敛，并记

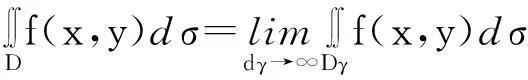
(1)

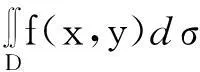
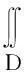
2非负函数反常二重积分收敛的判定

若f(x,y)是非负的，定义1等价于只要存在一列包围原点的光滑封闭曲线序列γn，满足Eγn⊂Eγn+1且当n→∞时dγn→+∞，其中Eγ为γn所围的有界区域，f(x,y)在Dn=Eγn∩D上可积，且极限(1)存在.由被积函数的非负性及单调收敛定理，极限存在等价于有上界.因此，对非负被积函数有下面的结论，见文献[1]P.280定理21.17.由定义1，下面定理条件的必要性是显然的.

定理2设在无界区域D上f(x,y)≥0，γ1,γ2,…,γn,…为一列包围原点的光滑封闭曲线序列，满足

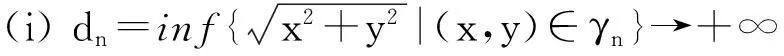
其中Dn=Eγn∩D，则反常二重积分(1)收敛，并且

正如上面的解释，利用定理2，要判断非负函数在无界区域上反常积分的收敛性及积分值，只需对为一列包围原点的光滑封闭曲线序列验证性质(i)和(ii)，同时得到积分收敛性和积分值.通常，选择En=[-n,n]×[-n,n]或者En={(x,y)|x2+y2≤n2}，γn为其边界.显然，γn满足(i).对于(ii)，由单调收敛定理，只需验证

例1证明反常二重积分

(2)

γn满足(ii).由定理2知，积分(2)收敛，且

注1文献[1]中证明例1的方法是利用P.281定理21.18.经比较，直接利用定理2更简单.

定理3设f(x),g(x)≥0，且无穷积分

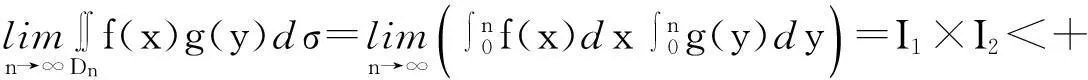
例2计算反常积分

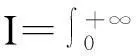
的值.

解考察二重反常积分

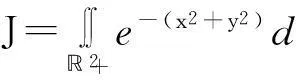
例3若p,q>0，则

证对Gamma函数Γ(p)，令x=u2，则dx=2udu，则

对Beta函数B(p,q)，令x=cos2θ，则dx=2cosθdθ，则

由定理3，有

=B(p,q)·Γ(p+q).

3一般函数反常二重积分收敛的判定

为了对一般函数反常二重积分收敛性进行判定，需要下面的Cauchy收敛准则.

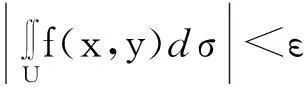
其中B(0,R)是以原点为圆心，R为半径的圆域.

证必要性是显然的，下证充分性.考虑函数

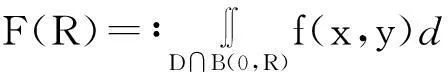
函数F(R)对所有的R有定义，且由Cauchy条件知，当R→+∞时，F(R)收敛，其极限记为I.∀ε>0，存在R>0使|F(R)-I|≤ε.对于平面上任一包围原点的光滑封闭曲线γ，且dγ≥R，有

定理5(比较判别法)设f(x,y)为定义在无界区域D上的二元函数.若对于平面上任一包围原点的光滑封闭曲线γ，f(x,y)在曲线γ所围的有界区域Eγ与D的交集Eγ∩D=Dγ上恒可积.又设满足同样条件的非负函数g(x,y)满足

|f(x,y)|≤g(x,y)，∀(x,y)∈D，

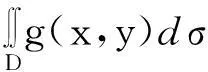
证直接由定理2和定理3立得.

例4设D=(-∞,+∞)×(-∞,+∞)，判断反常二重积分

的收敛性，并说明理由.当积分收敛时，求积分的值.

解首先证明I绝对收敛.令Dn=[-n,n]×[-n,n], 则当n→+∞时，dn→+∞，且

所以，I绝对收敛.其次，直接计算

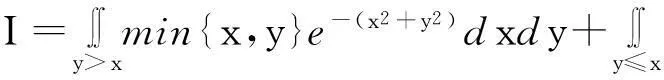
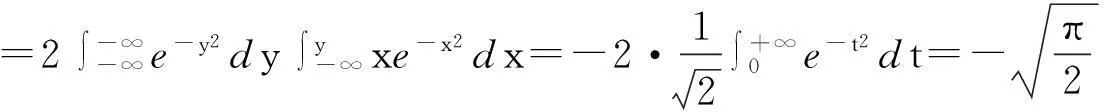
4条件收敛蕴含绝对收敛的直观理解

对于反常二重积分，可以证明：∫Df(x,y)dσ条件收敛，则必定绝对收敛 (见[1] P283定理21.19，或者证明见[2] P276定理13.4.2).这一点与反常一重积分有本质的不同.为了能直观上理解该性质，在本节中我们将以例子来给予分析和比较.由此，要判断一般函数反常二重积分的收敛，等价于判断其绝对值的非负函数积分的收敛，这已在第2节和第3节中讨论.

我们首先回顾无穷限反常一重积分的定义(参见[1]上册P272)，然后用例子说明，反常一重积分收敛与反常二重积分收敛不同性质的本质是由于定义不同造成的.

定义6设函数f(x)定义在无穷区间[a,+∞)上，且在任何有限区间[a,u]上可积，如果存在极限

则称此极限J为函数f(x)在[a,+∞)上的无穷限反常积分，记作

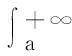
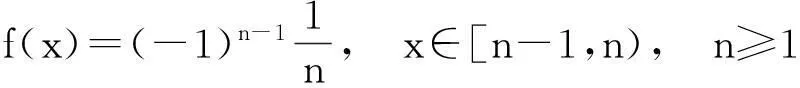
h(x,y)=f(x)g(y)，

其中f(x)与例5中相同，

现在来考察反常二重积分

是否收敛，是否绝对收敛.

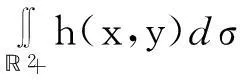
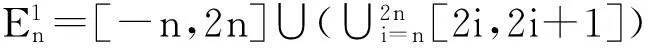
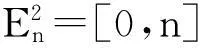
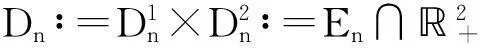
最后一个等式是因为数列

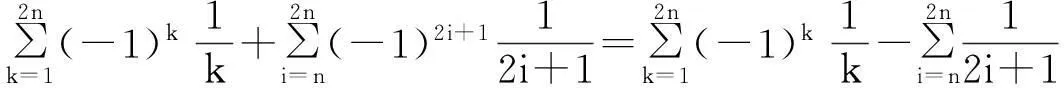
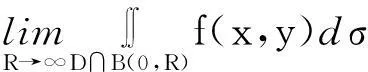
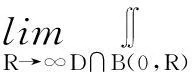
正是如此，反常二重积分必须是定义1中对任意的区域Dγ的极限来定义，而不是某类特别的区域.

另外，如果将定义6改为下面的形式，则反常一重积分与反常二重积分收敛性质相同.

定义6′设f(x)为定义在无穷区间[a,+∞)上的函数，若对R上任一包含原点的有界集合En，f(x)在En与[a,+∞)的交集En∩[a,+∞)=Dn上恒可积.设γn为En的边界，令

dn=inf{x|x∈γn}.

若极限

存在有限，且与En的选取无关，则称f(x)在[a,+∞)上的无穷限反常积分收敛，记作

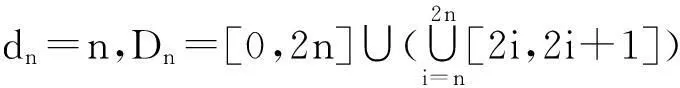
发散.

[参考文献]

[1]华东师范大学数学系. 数学分析(下册)[M]. 北京：高等教育出版社， 2014.

[2]陈纪修，於崇华，金路. 数学分析[M]. 2版. 北京：高等教育出版社， 2004.

[3]卓里奇B A. 数学分析[M]. 蒋铎，王昆杨，周美珂，邝荣雨译. 4版. 北京：高等教育出版社， 2006.

[4]崔尚斌. 数学分析教程[M]. 北京：科学出版社，2013.

[5]吴良森，毛羽辉，韩士安，吴畏. 数学分析学习指导书(下册)[M]. 北京：高等教育出版社，2004.

On Criteria for Convergence of Improper Double Integral

LIUJi-cheng,WANGXiang-jun

(School of Mathematics and Statistics, Huazhong University of Science and Technology, Wuhan 430074, China)

Abstract:The definition and criteria for convergence of improper double integral were introduced in Section 21.8 of “Mathematical Analysis”, written by Department of Mathematics, East China Normal University. We found that contents in this section are unclear; especially the conclusion of Theorem 21.19 is not intuitively explained. In this paper, we optimize contents of this section, rationalize the criteria for convergence of improper double integral, obtain a theorem to transform improper double integral on unbounded domain into an iterated integral, give the intuitive explanation of Theorem 21.19 and calculate some examples by using the framework in this paper. By analyzing the examples, our framework is very effective to judge the convergence and calculate the value of improper double integral.

Key words: improper double integral; absolute convergence; unbounded domain