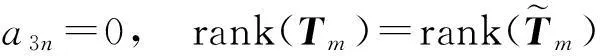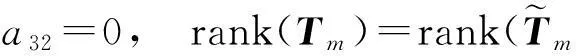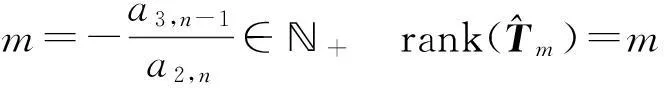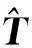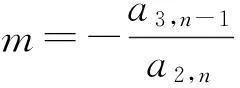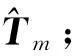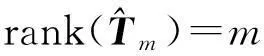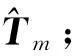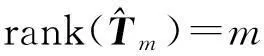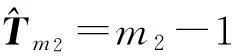一类多项式系数二阶线性微分方程解法的研究
一类多项式系数二阶线性微分方程解法的研究
胡亦郑1,李素梅2,罗勇1
(1. 温州大学数学与信息科学学院,浙江温州325035;2. 西安交通大学数学与统计学院,西安710049)
[摘要]给出了一类具有多项式系数的二阶线性微分方程有多项式型特解和通解的充要条件,并在Maple下实现了这类微分方程具有多项式型特解和通解自动判定和求解的算法.
[关键词]多项式系数; 多项式型特解; 算法实现
[收稿日期]2014-12-04
[基金项目]浙江省教育厅项目(Y2013127178)
[中图分类号]O175.1[文献标识码]A
1引言
二阶线性常微分方程
P(x)y″+Q(x)y′+R(x)y=f(x)
(1)
在自然与工程技术中有着极其广泛的应用,对于它的求解问题,也一直为大家所关注.
众所周知,如果已知(1)对应的齐次方程:
P(x)y″+Q(x)y′+R(x)y=0
(2)
的通解,利用常数变易法,即可求出(1)的通解. 而对于方程(2),如果已知它的一个特解,依照Liouville公式,可用积分的方法求出与线性无关的另一个特解,从而可求出它的通解[1],即
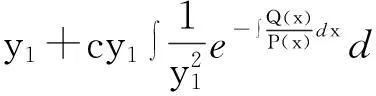
(3)
通过这种方法,将求解方程(1)的通解的问题转化为求方程(2)的一个特解的问题.在学习(2)这类方程时,可知当P(x),Q(x),R(x)为常数时,总是可解的,因此可以把这类方程看作"可解方程".但在实际问题上遇到的方程大多数不属于可解范畴.对于这类问题,通常会采用幂级数法,可以得到其在某邻域内的局域解,但这是无穷级数解或近似解;另外还有较多人提出不同的方法来解决一些具有某些特点的变系数方程,比如将一类变系数二阶线性常微分方程转化为已知的特殊的可解方程或者将变系数方程化为常系数方程等[2,3].
本文主要通过递推公式给出了系数为多项式的二阶线性齐次常微分方程存在多项式特解和通解的充要条件,该条件简单、易于判断,是一个可以算法化的条件. 进一步给出了Maple程序,实现自动判定和求方程的多项式型特解或通解.
2主要结论
引理1设A为n×m的矩阵,X为m维列向量,齐次线性方程组AX=0有非零解且非零解第一个分量不为零的充要条件是
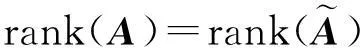
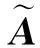
为AX=0的解.将AX=0写成分块矩阵方程的形式,即
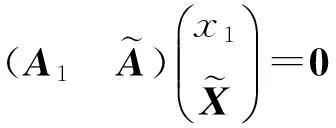
(4)
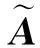
等价于矩阵方程(4)有解
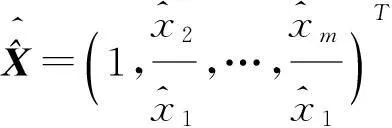
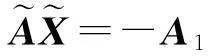
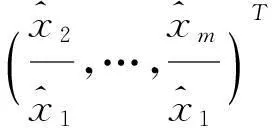
当且仅当
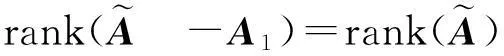
即有
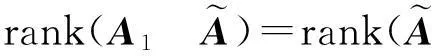
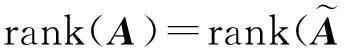
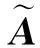
首先来讨论方程系数为2次多项式的情形.不妨设方程(2)的系数为
(5)
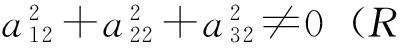
定理2具有(5)形式系数的二阶齐次线性常微分方程(2)存在m次多项式型特解的充要条件是
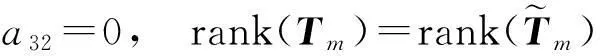
其中Tm为(m+2)×(m+1)矩阵,即

证若方程(2)具有一次多项式特解,即
y=A1x+A0(A1≠0),
则将y代入方程(2)的左边,有
左边 =a32A1x3+(a22A1+a31A1+a32A0)x2+(a21A1+a30A1+a31A0)x+a20A1+a30A0
这里
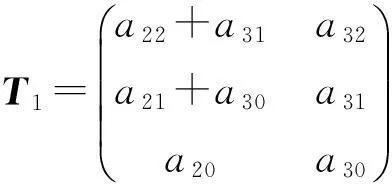
故由引理1可知,要使方程(2)恒成立,当且仅当有
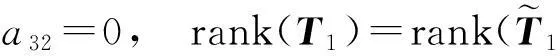
若方程(2)具有二次多项式特解,即
y=A2x2+A1x+A0(A2≠0),
则将y代入方程(2)的左边,有
左边 =a32A2x4+(2a22+a31)A2x3+(2a12+2a21+a30)A2x2+(2a11+2a20)A2x+2a10A2
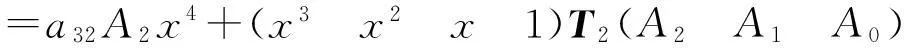
这里
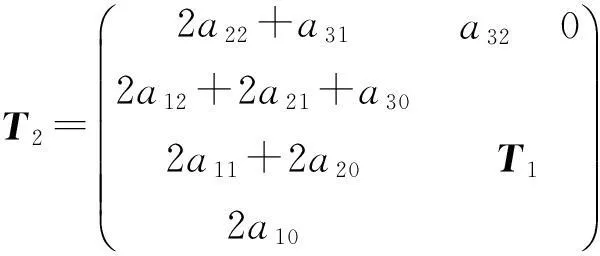
故由引理1可知,要使方程(2)恒成立,当且仅当有
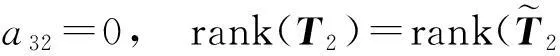
一般地,若方程(2)具有m次多项式特解,即
y=Amxm+Am-1xm-1+…+A1x+A0(Am≠0),
则将y代入方程(2)的左边,有
左边 =a32Amxm+2+(ma22+a31)Amxm+1+[(m2-m)a12+ma21+a30]Amxm
+[(m2-m)a11+ma20]Amxm-1+(m2-m)a10Amxm-2+a32Am-1xm+1
这里
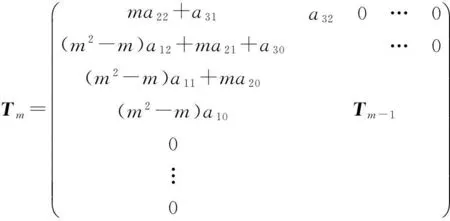
故由引理1可知,要使方程(2)恒成立,当且仅当有
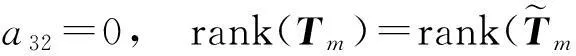
定理2得证.
定理3若a22≠0,则系数具有(5)形式的二阶齐次线性常微分方程(2)存在m次多项式型特解的充要条件是
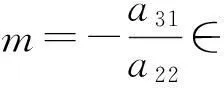
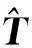
证由定理2可知,微分方程(2)具有m次多项式特解当且仅当
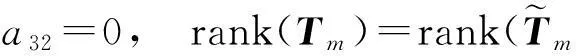
注意到Tm的第一行中第一个元素为ma22+a31,其余为0,故由
知必有
ma22+a31=0,
即
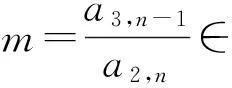
且Tm-1中对角线元素为
ka22+a31≠0,k=0,…,m-1,
即
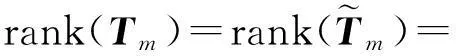
故在上述条件下,微分方程(2)具有多项式特解等价于
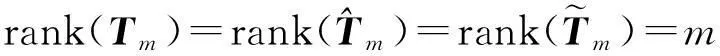
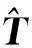
注由定理3知,当a22≠0,具有(5)形式的二阶齐次线性常微分方程(2)至多具有一多项式特解.
定理4系数具有(5)形式的二阶齐次线性常微分方程(2)存在多项式通解的充要条件是
a32=0,a22=0,a31=0,f(m)=m(m-1)a12+ma21+a30
有两个整数解m1 证由定理2,3可知,有 a32=0,a22=0,a31=0. 当a32=0,a22=0,a31=0时,注意到Tm中的 Tm(m+1,m+1)=0,Tm(i,i)=Tm(i,i+1)=0,i=1,2,…,m, f(m)=0,m∈+. 当f(m)=0有唯一正整数解m(可以是重根)时,注意到此时 f(k)≠0,k=0,1,…,m-1, 故TmX=0有一维的非零解,故只有唯一多项式特解,不能构成多项式通解.当f(m)=0有两个正整数解m1 当且仅当Det(Tm2,m1)=0.该充要条件得证. 接下来讨论方程系数为n次多项式的情形.不妨设方程(2)的系数为 (6) 定理5具有(6)形式系数的二阶齐次线性常微分方程(2)存在m次多项式型特解的充要条件是 其中Tm为(m+n)×(m+1)矩阵,即 证类似定理2的证明. 若方程(2)具有m次多项式特解,即 y=Amxm+Am-1xm-1+…+A1x+A0(Am≠0), 则将y代入方程(2)的左边 =m(m-1)a1,nAmxn+m-2+m(m+1)a1,n-1Amxn+m-3+…+m(m-1)a1,0Amxm-2 +ma2,nAmxn+m-1+ma2,n-1Amxn+m-2+ma2,n-2Amxn+m-3+…+ma2,0Amxm-1 +a3,nAmxn+m+a3,n-1Amxn+m-1+a3,n-2Amxn+m-2+…+a3,1Amxm+1+a3,0Amxm +a3,nAm-1xn+m-1+(xn+m-2xn+m-3…x1)Tm-1(Am-1…A0)′ =a3,nAmxn+m+(xn+m-1xn+m-2…x1)Tm(Am…A0)′, 这里 故由引理1可知,要使方程(2)恒成立,当且仅当有 定理5得证. 由定理5,类似于定理3、定理4的证明可知如下定理. 定理6若a2,n≠0,则具有形式(6)系数的二阶齐次线性常微分方程(2)存在m次多项式型特解的充要条件是 定理7具有形式(6)系数的二阶齐次线性常微分方程(2)存在多项式通解的充要条件是 a3,n=0,a2,n=0,a3,n-1=0,f(m)=m(m-1)a1,n+ma2,n-1+a3,n-2 有两个正整数解m1 rank(Tm1)=m1,rank(Tm2)=m2-1. 3算法和例子 在这节中将给出自动判定具有多项式系数的二阶线性常微分方程具有多项式型特解和通解的简单算法,并在Maple下实现了该算法,同时给出具体的例子进行验证. 算法: 输入:常微分方程(2)的系数P(x),Q(x),R(x)[a1,n,…,a10,a2,n,…,a20,a3,n,…,a30]. 输出:判定方程(2)是否存在多项式特解或通解. 若是,给出特解或通解. PS={二阶线性常微分方程(2)系数a1,n,…,a10,a2,n,…,a20,a3,n,…,a30} 若a3,n≠0返回(无多项式特解); 若a2,n≠0 求解线性方程TmX=0的非零解,构造并返回(多项式特解) 否则返回(无多项式特解); 否则/* 即:a2,n=0 若a3,n-1≠0返回(无多项式特解); 求解m(m-1)a1,n+ma2,n-1+a3,n-1=0,设解为m1,m2; 若m1,m2都不是正整数,返回(无多项式特解); 若m1,m2中只有一个是正整数,设为m 求解线性方程TmX=0的非零解,构造并返回(多项式特解) 否则返回(无多项式特解); 若m1,m2都是正整数,设m1 求解线性方程Tm2X=0的非零解,构造并返回(多项式通解) 否则返回(无多项式通解). 例1求(x2+x+1)y″+(x2+2x+1)y′+(-x-1)y=0的多项式特解. 解输入系数多项式 P(x)=x2+x+1,Q(x)=x2+2x+1,R(x)=-x-1; 利用算法,输出 存在多项式型特解,特解是y=x+1. 例2求(-1/3x2+x+18)y″+(x+1)y′-y=0的多项式通解. 解输入系数多项式 P(x)=-1/3x2+x+18,Q(x)=x+1,R(x)=-1; 利用算法,输出 存在多项式型特解,特解是y=x+1,y=-972-27x2+x3, 故有多项式型特解,通解是y=C1(x+1)+C2(-972-27x2+x3). 例3求如下多项式 (x5-23323/60x4-23323/360x3-23323/2160x2-23353/12960x+6/5)y″ +(23333/2592-6x4+23321/12x3+23321/72x2+23321/432x)y′ +(1/36+6x3+x2+1/6x)y=0 的通解. 解输入系数多项式 P(x)=x5-23323/60x4-23323/360x3-23323/2160x2-23353/12960x+6/5, Q(x)=23333/2592-6x4+23321/12x3+23321/72x2+23321/432x R(x)=1/36+6x3+x2+1/6x 利用算法,输出存在多项式型特解,特解是y=-23333+72x,y=432-5x2+432x6,故有多项式型通解,通解是 y=C1(72x-23333)+C2(432-5x2+432x6). [参考文献] [1]东北师范大学微分方程教研室. 常微分方程[M].北京:高等教育出版社,2005. [2]阎恩让. 变系数二阶线性微分方程可解的充要条件[J].西安电子科技大学学报(自然科学版),2004,31(5):796-800. [3]孙智勇. 变系数二阶常微分求解的基本研究及Maple在其中的应用[M]. 沈阳:东北师范大学,2006. The Study of the Solutions for a Second Order Linear Differential Equation with Polynomial Coefficients HUYi-zheng1,LISu-mei2,LUOYong1 (1. College of Mathematics and Information Science , Wenzhou University,Wenzhou Zhejiang 325035, China; 2. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049 ,China) Abstract:The sufficient and necessary condition that there exists the polynomial particular solutions and the generalized solutions of a second order linear differential equation with polynomial coefficients is given. And it is realized to automatically determine whether the second order linear differential equation with polynomial coefficients has polynomial particular solutions and the generalized solutions and to automatically solve the polynomial particular solutions and the generalized solutions in Maple. Key words: polynomial coefficient; polynomial particular solution; algorithm