区域高等学校科技发展效率评价研究

区域高等学校科技发展效率评价研究

刘鑫桥

（中国人民大学教育学院，北京 100872）

摘 要：科学地评价不同区域内高等学校的科技投入产出效率是合理优化资源配置及充分利用有限教育投入的关键，对我国产出更多顶尖科研成果，提升中国高等教育在世界范围的竞争力至关重要。DRF－DEA两步法将因子分析与数据包络分析的优点相结合，以区域高等学校科技效率评价为中心，采用因子分析将综合评价指标体系的投入与产出指标提取出意义明确的公因子降维，利用DEA模型计算各区域的效率并进行排序，研究结果表明：高等学校科技发展的总效率均值较低，纯技术效率均值较高；多数区域高等学校科技发展处于无效率的状态，DEA无效主要原因在于规模过小；高等学校科技发展的投入不足，继续增大投入可以达到规模收益递增的效果。

关键词：因子分析；数据包络分析；科技效率；超效率DEA

中图分类号：G648 文献标志码：A

收稿日期：2014－10－23

基金项目：北京市教育委员会共建项目“高等教育与城市创新能力研究”（2008994008）的阶段性成果之一

作者简介：刘鑫桥（1989－），男，山东泰安人，中国人民大学教育学院硕士研究生，主要从事教育经济、教育管理以及教育政策研究。

一、问题的提出

科学技术是推动一个区域经济社会发展的第一生产力，而区域内的高等学校是推动科学技术进步的重要支撑，是科学技术创新体系中的重要组成部分。科学地评价区域高等学校的科技投入产出效率是必要的和紧迫的，合理的优化资源配置及充分利用有限的教育投入，对产出更多顶尖科研成果，提升中国高等教育在世界范围的竞争力至关重要。国内外采用数据包络分析（DEA）中经典的CCR、BCC模型及拓展的SE－DEA、C2GS2等多种模型对高校的投入产出效率进行了一系列评价研究，主要分成两类：一类是关注不同高校个体之间的科研、创新及管理的效率，如罗杭采用超效率DEA对中国的“985”工程大学展开效率评价［1］，尹伟华采用Bootstrap修正的DEA方法对教育部直属高校科研效率进行全面的分析评价［2］；另一类是关注不同区域间高校的科技、科研及创新等效率，如周静等采用DEA模型对29个不同地区高校的科技创新效率进行比较研究［3］。

上述研究，无论对高校哪种效率的评价，虽然所研究的主题不同，但研究思路与过程均较为类似，均是通过构建评价指标体系，然后采用模型进行实证分析，根据数据分析结果给出结论与建议。早期的研究所采用的模型较为简单，随着适合多投入、多产出系统的DEA模型的引入，使实证分析结果更加科学合理。但它们也存在一个明显的不足：研究中所构建的指标体系指标数目较少，不能全面地反映决策单元的特征。当然，出现这一问题的原因在于DEA模型对决策单元个数与投入产出指标个数之间的限制，研究表明：决策单元个数一般应为投入产出指标个数的三倍［4］，而我国的内地省（市、自治区）数量为31个是客观不变的，在此限制下构建全面的投入产出指标体系非常困难，只能进行人为主观的取舍，因此，在不全面指标体系基础上进行的效率评价，其科学性也就受到质疑。如何尽量减少主观性的选择指标，从本质上突破指标数量的限制至关重要。DRF－DEA两步法将因子分析与数据包络分析的优点相结合，首先采用因子分析将评价指标体系的投入与产出指标提取出意义明确的公因子，达到降维的目的，然后从投入角度采用CCR、BCC、超效率DEA计算出总效率EFF、纯技术效率TE、SEDEA值，并通过上述结果分析出规模效率SE、规模收益情况RTS及效率综合排名。

二、DRF－DEA两步法的原理与步骤

（一）第一步，DRF数据降维

因子分析（DRF）以相关性为基础，从数据内部的特征出发，在协方差矩阵或相关矩阵的基础上将错综复杂的原始指标综合成较少的公共因子。这些因子能够反映原始指标的绝大部分信息（方差），之间却不存在相关性，从而达到数据压缩降维的目标。

（二）第二步，DEA效率评价

数据包络分析（DEA）是基于线性规划评价相同类型组织相对有效性的非参数模型，其允许多投入、多产出的特点相对其他评价方法具有绝对优势。最初的DEA是由Charnes和Cooper在规模报酬不变基础上引入的CCR模型，其评价结果称为决策单元的总效率。随后Banker等引入规模报酬可变的BCC模型，其评价结果称为决策单元的纯技术效率。总效率可以分解为纯技术效率与规模效率。在采用CCR、BCC计算效率时凡是有效的决策单元其效率值均表示为1，因此无法比较同时有效的决策单元之间的效率高低，在经典DEA模型基础上放松效率值不大于1的约束，引入超效率DEA可以对决策单元总效率进行充分排序。

（三）DRF－DEA两步法的优势

DRF与DEA结合的优势主要体现在三个方面：一是在根本上突破了DEA模型对投入产出指标个数与决策单元个数之间的限制，在构建指标体系时，可以完全从决策目标的内涵出发，抛开对投入产出指标个数的考虑；二是杜绝了指标体系中各项指标之间的相关性对效率评价结果的影响，囿于知识的局限性，在构建指标体系的过程中可能无法发现不同指标之间具有强相关性，但是进行因子分析提取的公因子之间不存在相关性，从而让效率评价结果更科学；三是减少AHP等方法主观上对指标主次的赋权，让其更科学地反映评价目的与评价内容。另外，在因子分析对投入产出指标降维提取的公因子的过程中，可以获得因子得分，清晰地反映决策单元所处实际水平，在后续效率评价的过程中，充分考虑各类投入产出的多少，从而达到多层次、多目标综合评价的效果。

三、决策单元选择与指标体系构建

（一）决策单元的选择

决策单元（DMU）的选择是进行DEA分析的基础，研究区域高等学校的科技投入产出，“区域”的界定非常关键，考虑到同一区域内政策及经济环境的内在一致性，直接按行政区划将其分为31个区域作为决策单元更合理［5］。同时将31个省市划分为31个区域作为决策单元满足DEA模型的要求：DMU必须是相同的类型、在同一市场环境下运作、具有相同的任务与目标等［6］。

（二）指标体系的构建

区域内高等学校的科技投入与产出均包括多个方面，科学的评价指标体系应是客观系统、可比性强，并且是可操作的。采用逐步分解的方法，可将科技投入与科技产出分别作为一级指标，科技投入中包含人力资源的投入、经费的投入以及机构项目数的投入三个二级指标，分别寻找能体现其内涵的三级指标，包括教学与科研人员（X1）、研究与发展人员（X2）、R＆D成果应用及科技服务人员（X3）、参与研究生数（X4）、研究与发展机构数（X5）、研究项目数（X6）、基础研究经费（X7）、应用研究经费（X8）、试验发展经费（X9）、R＆D成果应用经费（X10）、科技服务经费（X11）；科技产出包括数量产出和商业转化金额产出两个二级指标，包括出版科技著作数（Y1）、发表学术论文数（Y2）、国外学术刊物论文数（Y3）、国际级项目验收（Y4）、专利申请数（Y5）、专利授权数（Y6）、专利出售总金额（Y7）、技术转让合同金额（Y8）等八个三级指标。研究中为保证统计数据的权威性及统计口径的一致性，所用数据均来源于教育部科学技术司编写的《2012年高等学校科技统计资料汇编》。

四、区域高等学校科技效率评价的实证分析

（一）基于DRF的投入产出指标降维

采用SAS软件对科技投入的11个三级指标X1—X11进行因子分析，KMO值为0．828，说明指标间存在较强的相关性，适合于DRF降维，因子分析结果如表1，通过方差最大化旋转后的因子载荷阵可以看出公因子11在X4、X6、X7、X8、X9、X10六个指标上有较大的载荷，反映了区域科技投入中的财力投入，因此可以称为财力投入因子；公因子I2在X1、X2、X3、X5、X11五个指标上有较大的载荷，反映了区域科技投入中的人力投入，因此可以称为人力投入因子。采用同样的方法及步骤对科技产出的八个三级指标Y1～Y8进行DRF降维，KMO值为0．719，提取出一个公因子O1，可称为产出因子。

由于SAS给出的因子得分有非正数存在，代表低于平均水平，但是采用DEA进行投入产出效率分析时，负数不符合要求，因此对因子得分进行转换，公式如下：

表1　因子载荷阵与方差贡献率

其中A是因子得分，i代表区域，i∈［1，31］，j代表公因子，j∈［1，3］。标准化之后的因子得分介于1与10之间，上述变换并不影响原变量的本质含义。转换之后的投入产出数据如表2所示，可以发现在财力投入方面，北京、上海、江苏居于前列，三个区域的科技经费投入与直观上的经济发展水平相符；在人力投入方面，江苏、辽宁、广东三个区域在前三位；而在科技产出方面，北京、江苏、上海三个区域在前三名。

三项指标的数值排名与普遍的认识比较一致，经济发达地区在财力投入方面较多，而经济落后地区的投入比较少；高校数量多的地区在人力投入方面会比较充足，同时区域内的重点高校的数量也影响了科技人力资源的投入；科技产出受投入的影响，无论财力资源还是人力资源投入多的地区，科技产出均比较丰富。

表2　标准化的高等学校科技投入产出指标及排名

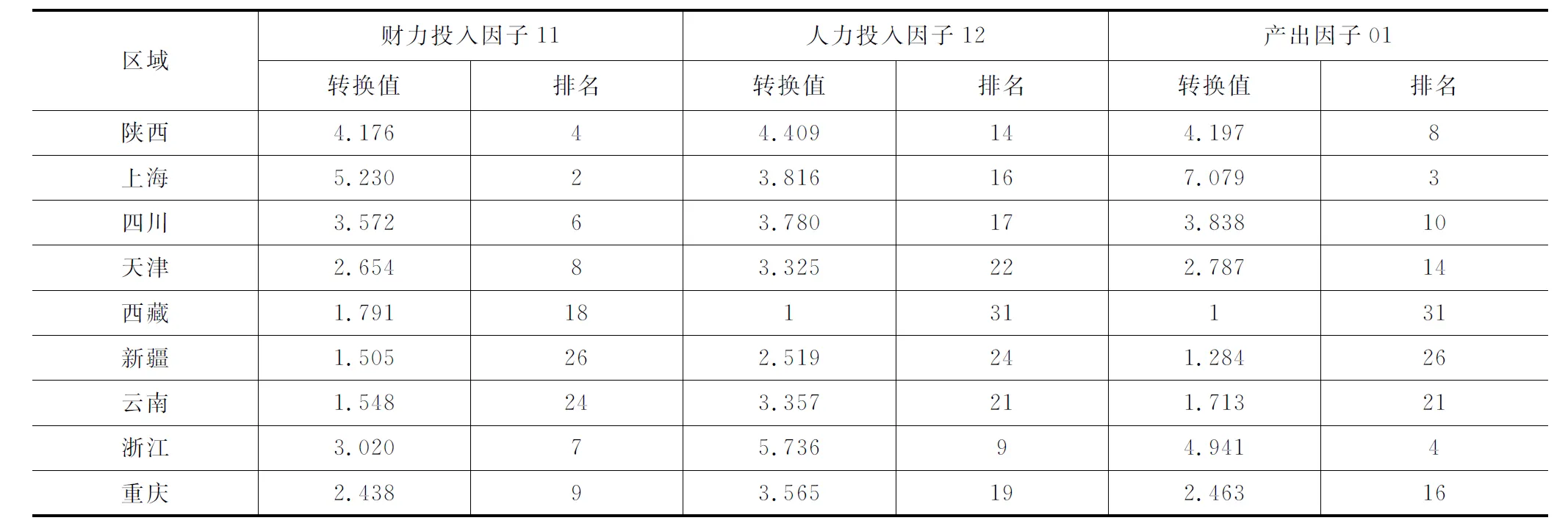
续表2

（二）基于DEA的科技效率综合评价

根据表2中标准化后的区域高等学校科技投入因子与产出因子的数据，分别从投入角度采用CCR、BCC、超效率DEA计算出总效率EFF、纯技术效率TE、SE－DEA值，并通过上述结果分析计算出规模效率SE、规模收益情况RTS及超效率综合排名，结果如表3。

表3中显示，根据CCR计算出的总效率均值为0．697，说明当前区域高等学校的科技投入产出效率不高，其中有北京、河南、上海、江苏四个地区的值为1，四个地区的投入产出是有效的，达到生产前沿线。其他27个区域是无效的，在产出保持不变的情况下可以减少投入或者在投入不变的情况下增加产出，青海、西藏、海南三个区域在总效率的后三位。根据BCC计算出的纯技术效率均值为0．915，说明各区域的资源浪费状况较低，总效率低并不是资源浪费造成的，其中北京、河南、上海、江苏、广西、新疆、海南、西藏、青海等九个区域值为1，这些区域的科技投入相对其他22个区域是有效的，不存在资源浪费的状况，其中广东、陕西、吉林三个区域的纯技术效率居后三位，均低于0．8，说明三个区域有超过20%的科技投入没有达到最适合的产出。根据总效率与纯技术效率可以计算出规模效率来说明决策单元是否处于最适合的规模，规模效率的平均值为0．768，当前我国高校科技投入产出的总体规模效率水平不高，同时结合规模收益情况，北京、河南、上海、江苏、辽宁五个区域规模报酬不变，其他26个区域的规模效率均低于1，规模报酬递增。

采用超效率DEA模型进一步计算出SE－DEA值并按其大小排序，可以清楚地看出各个区域的效率排名，北京、河南、上海排在前三名，而海南、西藏、青海排在后三名。

表3　DEA效率评价分析结果

续表3

按照《中国统计年鉴》中的东部地区、西部地区、中部地区、东北地区划分方法，四个地区的平均效率如表4所示。东北地区的总效率与规模效率最高，东部地区与东北地区比较接近，仅有西部地区的总效率低于全国平均值，也就是东部、东北地区的投入产出效率是高于中部、西部地区的，改善西部地区的总效率更有助于全国总效率的提高。西部地区的纯技术效率最高，规模效率最低，造成西部地区总效率低的原因主要在于规模效率低，而其投入资源是非常能有效利用的，提高西部地区的效率应该从改善其规模效率入手。东部地区与东北地区在三种效率上的平均值都与全国的平均值差异不大，因此，关注中部与西部地区效率的提高，对全国范围的效率提高至关重要。

表4　四个地区的平均效率

五、结论及建议

本文采用DRF－DEA两步法对31个省（市、自治区）的高等学校科技投入产出效率进行分析，通过因子分析提取出能够充分反映投入产出的公因子，对指标体系达到降维的效果，克服了DEA模型对决策单元与投入产出指标个数之间的约束，增强了分析结果的科学性。实证结果表明：北京、河南、上海、江苏的总效率和规模效率是有效的，北京、河南、上海、江苏、广西、新疆、海南、西藏、青海的纯技术效率是有效的。

将31个区域分为四类：一类区域的高等学校处于最优科技效率状态，纯技术效率与规模效率均为1，有北京、河南、上海、江苏四个区域，处于最优生产规模及相对有效率的状态；二类区域的高等学校短期内易改善为最优状态，0．9＜纯技术效率＜1，0．9＜规模效率＜1，该类区域短期内调整投入产出量，非常容易达到最优生产规模及相对有效率的状态，符合条件的仅有黑龙江、浙江两个区域；三类区域的高等学校处于生产无效率的状态，纯技术效率＜0．9，规模效率≈1，包括辽宁、山东、广东、湖北、湖南、陕西六个区域；四类地区的高等学校科技发展处于规模过小的状态，规模效率＜0．9且规模收益递增，其规模过小造成固定成本相对较高，平均成本提高，可以通过增大规模扩大产出达到最优，包括河北、安徽等19个区域。

从以上分析结果可以发现当前我国多个省市的高等学校科技发展依旧处于无效率的状态，区域的高等学校科技效率与经济发展水平有较强的相关性，大部分地区的DEA无效是因为规模过小造成的，国家对高等学校科技发展的投入不足，继续增大

投入可以达到规模收益递增的效果。提高高等学校科技效率应当从以下三个方面入手。

1．大力增加高等学校的科技投入，促进产生高水平的科技产出。全国有26个区域的规模收益是递增的，足以证明当前的科技投入是不充足的，增加科技投入、扩大规模，促进高校科技水平的发展是可行的。

2．依据纯技术效率对不同区域间的投入调整。要减少纯技术效率低的区域的投入，发挥资源杠杆的作用，刺激各区域改善资源利用状况，对纯技术效率高的区域进行更多的资金、人力投入，让有限的资源得到更有效的配置和利用。有些区域如陕西、湖北等高校数量众多，纯技术效率却较低，应该深刻反思在资源利用上的缺陷，做到将区域内的资源投入发挥最大效用。

3．鼓励区域间的学习借鉴。当前不同区域间的效率差距巨大，总效率最高的北京的效率值是总效率最低的青海的效率值的近六倍，一半左右的区域总效率及纯技术效率均低于平均值，因此，引导效率低的区域向效率最优地区学习是至关重要的。

参考文献：

［1］罗杭．2011年中国“985”大学效率评价———效率水平排序，影响因素研究与松弛变量分析［J］．清华大学教育研究，2013 （2）：87－95．

［2］尹伟华，袁卫．基于Bootstrap－DEA方法的中国教育部直属高校科研效率评价［J］．统计与信息论坛，2013，28（6）：61－69．

［3］周静，王立杰，石晓军．我国不同地区高校科技创新的制度效率与规模效率研究［J］．研究与发展管理，2005，17（1）：109－117．

［4］Pedraja－Chaparro F，Salinas－Jimenez J，Smith P．On the Quality of the Data Envelopment Analysis Model［J］．Journal of the Operational Research Society，1999，50（6）：636－644．

［5］刘鑫桥．高等教育发展水平与效率的不一致性———基于因子DEA方法的实证分析［J］．中国人民大学教育学刊，2014（1）：39－55．

［6］Banker R D，Charnes A，Cooper W W．Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis［J］．Management Science，1984，30（9）：1078－1092．

On the Evaluation of Technological Development Efficiency of Colleges in Different Regions

LIU Xin－qiao

（School of Education，Renmin University of China，Beijing 100872，China）

Abstract：Scientific evaluation on the technological input－output efficiency of colleges in different regions，on one hand，is pivotal to optimize resource allocation and make the most of finite educational input．On the other hand，it＇s vital for more scientific achievements production and enhancing the competitiveness of China＇s higher education worldwidely．DRF－DEA combines the advantages of both factor analysis and data envelopment analysis（DEA）．Based on DRF－DEA method，the paper extracts objective common factors from all the input and output indicators of the evaluation index system，which is centered in the evaluation of regional college technology efficiency，for dimension reduction．On this basis，the DEA model is applied to calculate and then rank the efficiency values of all the regions．Empirical results show that the mean of total efficiency is low while the mean of pure technology efficiency is relatively high．The technology developments of most regions＇colleges are inefficient，which mainly results from their too small scale and insufficient input for technology development．Furthermore，continue to increase the input can achieve increasing return to scale．

Key words：factor analysis；data envelopment analysis；technology efficiency；Super－Efficiency DEA

（责任编辑朱春花）