巧妙设计 打造高效的数学课堂练习
李必虎
【关键词】巧妙设计 数学练习 小学数学
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2015)11A-0059-01
练习是有效的思维训练方式,也是基本的课堂教学形式,有助于学生理解数学知识和掌握数学技能。如何进行有效的练习设计,提升学生的数学思维呢?笔者认为,教师要充分考虑学生的层次和水平,将枯燥乏味的数学练习变成美味的营养大餐,一方面激发学生的兴趣,另一方面为学生提供思维动力。
一、过渡练习,调动数学胃口
在小学数学新授课堂中,学生对新知的掌握仅限于活动探究,并没有获得实际意义上的内化和巩固,因而需要教师根据教学内容,设计相应的过渡练习,充分展示学生的思路,调动学生的数学胃口。
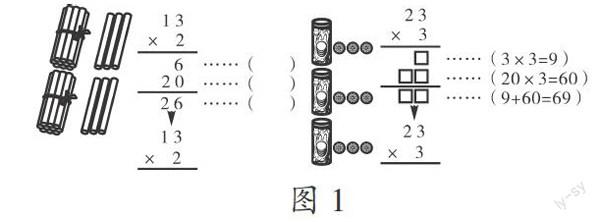
例如,在教学北师大版二年级数学下册《两位数乘一位数的算法》时,教学的重点是要让学生掌握两位数乘一位数的笔算方法,教学的难点是理解两位数乘一位数的算理。对于数学计算教学来说,核心思想是要让学生在理解算理的基础上掌握算法。为了使学生获得知识的内化,笔者设计了这样一组过渡练习:黄瓜有13行,每行有2棵,一共有多少棵?书包的价钱是文具盒的3倍,文具盒23元/个,书包多少钱?学生分别列出竖式(如图1)进行计算,由此理解算式的意义。在理解算理的基础上,学生认为在竖式计算时,要将两位数写在上面,一位数写在下面,然后个位对齐,用两位数中的个位去乘一位数,再用两位数的十位去乘一位数,两个积相加就得到乘积。
在以上练习设计中,教师突出了位值的分解,利用数形结合的方式,顺利过渡到竖式计算,并能够有效沟通算理和算法之间的联系,打开了学生的思维空间。
二、变式练习,提高数学素养
有效的课堂练习,一方面取决于内容,另一方面则取决于多种形式的综合呈现。在小学数学新授课教学中,教师要深入钻研教材,将复杂的数学内容转变为简约的变式练习,通过学生的思维碰撞,从不同的侧面揭示知识的本质,从更多的角度去理解、巩固所学知识,使学生的营养全面均衡,提高数学素养。
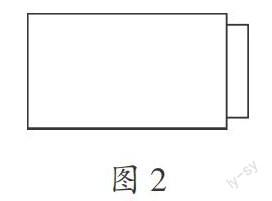
例如,在教学北师大版二年级数学下册《认识长方形和正方形》时,在学生基本掌握了长方形和正方形的概念之后,笔者设计了这样的变式练习:(1)信封中有一个四边形(如图2),四个角都是直角,你能根据露出的这一个角,猜出图形是什么吗?(2)露出的部分长、宽各是多少?根据露出的部分,猜出它是什么形状?学生认为可能是长方形,也可能是正方形。此时笔者继续变式:如果信封里的图形是正方形,那么边长是多少?学生通过测量得露在外面的边长为8厘米。此时笔者继续引导:如果信封里的图形是长方形,长可能是8厘米,那么它的宽会比8厘米怎样?学生认为,如果长是8厘米,那么宽就就会比长短一些。如果信封里的图形是长方形,宽可能是8厘米,那么它的长会比宽怎样?学生根据长方形长、宽的关系,认为长应该比8厘米长。由此,学生对长方形和正方形的基本特点有了直观的认知。
这样的变式练习,既能有效促进学生的积极思考,又有助于学生对长方形的长和宽的理解和把握,同时训练了学生的逆向思维,提高了学生的数学素养,为下一步巩固长方形的特点奠定了基础。
三、开放练习,发展数学思维
如果说过渡练习是开胃小菜,变式练习是正餐的话,那么开放练习就是一道甜点,一方面满足学有余力的学生,另一方面则抓住学生思维活动的焦点,使学生感到真实、新奇、有趣,使思维潜移默化地向高层次迈进,拓展思维空间。
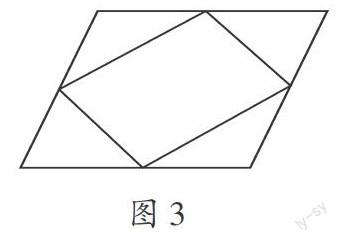
例如,在教学北师大版五年级数学上册《平行四边形的面积》时,笔者设计了这样的开放练习:(如图3)大平行四边形的底边是10厘米,高是8厘米,连接大平行四边形的四条边的中点,形成一个小平行四边形,求小平行四边形的面积。
在解决这道练习题时,有的学生采用添加辅助线的方法进行比较和推理,从而得出小平行四边形的面积是大平行四边形面积的的一半;有的学生将这个平行四边形先看做一个长方形,推理出小平行四边形的面积等于大平行四边形面积的一半,再从特殊到一般,推理出小平行四边形的面积是原来大平行四边形面积的一半。这样的练习设计,大大地促进了学生思维的发展。
总之,教师要巧妙设计,本着“练习有量但不过量,训练到位而不越位”的原则,设计有效的过渡练习、变式练习和开放练习,为学生提供营养丰富的数学大餐。
(责编 林 剑)

