两难区影响因素与控制策略

刘润乔， 韩加蓬， 刘洪光

(山东理工大学 交通与车辆工程学院， 山东淄博255049)

两难区影响因素与控制策略

刘润乔， 韩加蓬， 刘洪光

(山东理工大学 交通与车辆工程学院， 山东淄博255049)

摘要：通过建立车速时变的两难区数学模型来获取各车辆两难区长度范围，研究分析车速、黄灯时间、车辆加减速度、反应时间与两难区之间的影响关系.根据黄灯启亮时车辆的加减速情况，采用黄灯时间由小到大循环判断的预测方法，提出两难区车载预警和黄灯时间控制策略，该策略可有效降低车辆陷入两难区事件的发生概率，减少交叉口车辆交通事故.

关键词：车速时变；车载预警；黄灯时间预测；两难区影响因素

两难区是驾驶员在交叉口处既通不过也停不下的区域，即驾驶员在看到黄灯启亮后既不能安全停在停止线上，又不能在不超速违规行驶的前提下顺利通过交叉口，无论驾驶员选择停还是行，在红灯期间都将落在交叉口内[1].迄今为止国内外学者在黄灯时间调整和两难区车载预警控制中已获得了大量研究成果：王金梅等[2]分析了两难区与被动闯红灯的联系，通过对困境区域车辆的举例分析，表明正确设置黄灯时间和安装闯红灯自动拍摄装置对防止陷入两难区和闯红灯有重要意义；黄玮等[3]研究分析两难区的产生原因和理论黄灯时间的计算方法，提出了采用感应信号逻辑控制降低车辆陷入交叉口两难区的概率；Carroll等[4]进行了绿灯终止提前警告系统的设计和安装，实测结果表明该警告系统可使闯红灯现象减小40%～45%，有效地减小车辆陷入两难区的概率.本文研究分析两难区影响因素，设计车路协同方式下的两难区车载预警控制策略，根据黄灯启亮时车辆的加减速情况，提出车辆加速和减速情况下的两难区车载预警控制策略，研究设计两难区黄灯时间调整控制策略，采用黄灯时间由小到大循环判断的预测方法，获取解决两难区问题的最佳黄灯时间.

1 两难区影响因素研究分析

1.1两难区的确定

1)黄灯启亮时，对于那些还未越过停止线的车辆，要想在红灯启亮前安全停靠于停车线前，那它离停止线的距离必须大于不同情况下的停止距离L1，该距离可表示为：[5]

(1)车辆实际停止距离

(1)

式中：v为车辆实际速度(m/s);Tr为驾驶员反应时间; a为车辆实际制动减速度.

(2)车辆以最高限速行驶的最小停止距离

(2)

式中：v0为交叉口车辆最高限速(m/s); a1为普通制动下车辆制动减速度最大值.

(3)实际车速下车辆的最小停止距离

(3)

式中：v为车辆实际速度(m/s); a1为普通制动下车辆制动减速度最大值.

2)黄灯启亮时，对于那些还未越过停止线的车辆，想要在红灯启亮前不超速顺利通过交叉口，那它离停止线的距离必须小于不同情况下的通过距离L2，该距离可表示为：

(1)车辆实际通过距离

(4)

式中：v为车辆实际速度(m/s);L0为机动车的长度(m);Ty为黄灯时间(s);W为交叉口的直径(m);a为车辆实际加速度.公式(4)曲线如图1所示.

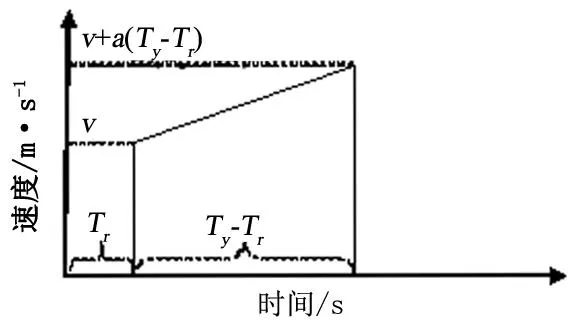
图1　车辆以加速度a通过交叉口的速度-时间变化图

(2)车辆在最高限速下的最大通过距离

(5)

式中：v0为交叉口车辆最高限速(m/s)，a0为车辆最大加速度.公式(5)曲线如图2所示.

图2　车辆在最高限速下通过交叉口的速度-时间变化图

3)传统两难区数学模型[6]采用公式(2)和公式(5)建立，此模型的精确度不是很高，因为假设车辆以最高限速行驶的最小停止距离作为停车基准线，由图3可知，如果车辆离停车基准线的距离小于此值，则不能停下来，如果车辆以实际速度下的最小停止距离作为停车基准线，则处在L1和L2之间的车辆可以停下，这与以最高限速行驶的最小停止距离作为停车基准线时得出的结论不符，故本文根据交叉口车辆速度时变性，采用公式(3)和公式(5)建立两难区数学模型.

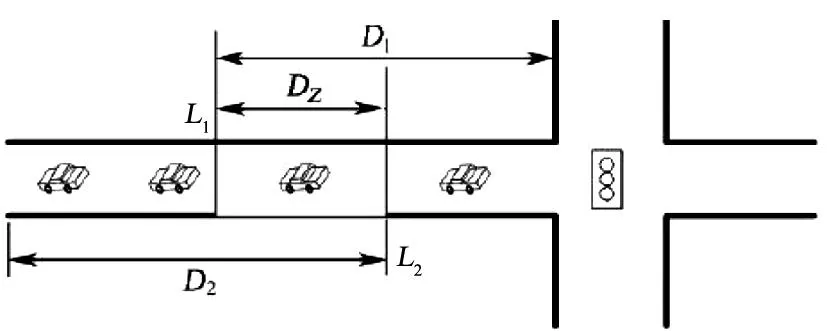
图3　两难区区域长度示意图

1.2两难区的长度

1) 黄灯启亮时，对于那些还未越过停止线的车辆，要想在红灯启亮前安全停靠于停车线前，应满足如下条件[7]：

(6)

2) 黄灯启亮时，对于那些还未越过停止线的车辆，在红灯启亮前能不超速且顺利通过交叉口，应满足如下条件：

(7)

如果式(6)和式(7)同时不满足的话，则

(8)

两难区区域长度如图3所示.图3中D1为不满足式(6)的区域长度；D2为不满足式(7)的区域长度；DZ为两难区区域长度，可以用L1与L2之差表示，即

(9)

(1)若DZ>0，L1>L2(如图4所示),则此情况下存在两难区域，DZ值越大，两难区区域长度越大，车辆陷入两难区的概率越大.

图4　L1>L2时两难区示意图

(2)若DZ>0,L1

图5　L1

(3)若DZ=0,L1=L2(如图6所示)，则此情况下两难区域为一条线，也就不存在两难区域.

图6　L1=L2时两难区示意图

1.3针对两难区影响因素研究分析

两难区是一个时空概念区域，车辆是否会陷入两难区，不仅与驾驶员的反应时间有关，还与车辆此时所在的位置、速度、制动减速度以及黄灯时间有密切关系[8].

车辆在不违章超速前提下，利用式(9)对车辆车速v、最大减速度a1、最大加速度a0和驾驶员反应时间Tr以及黄灯时间Ty进行研究分析，得到：

(10)

(11)

(12)

(13)

(14)

从式(10)和(11)可以看出a0和a1都相对于DZ的偏导数小于0，两难区域长度DZ随着a和a1的增大而减小，呈递减关系，表明车辆的动力性和制动性能越好，陷入两难区的可能性越低，但车辆加速度过大影响车辆的操作稳定性和行驶安全性，加大车辆追尾和急刹车事件的发生.

从式(12)可以看出Tr相对于的DZ偏导数大于0，表明两难区域长度DZ随着驾驶员反应时间Tr的增大而增大，呈递增关系.然而个人反应时间因人而异，且影响条件很多，比如驾驶员在酗酒或疲劳状态下反应时间都会加大，无疑加大了车辆陷入两难区的概率.

从式(13)可以看出Ty相对于DZ的偏导数小于0，说明两难区域长度DZ随着黄灯时间Ty的增大而减小，呈递减关系.虽然黄灯时间的延长有利于减小陷入两难区的概率，但过长的黄灯时间会增加驾驶员在交叉口处的等待时间，影响交叉口车辆的通行效率.

从式(14)看不出车速与两难区域长度的递增、递减关系.可将交叉口车辆最高限速设为10m/s，驾驶员反应时间设为1s，车辆普通制动减速度最大值a1设为3m/s2，车辆最大加速度设为3m/s2，车长L0为5m，交叉口的直径W=15m，则式(9)可变为

(15)

图7为速度-黄灯时间-DZ关系图.

图7　速度-黄灯时间-DZ关系图

如果交叉口黄灯时间为定值4s，则式(15)变为

(16)

将式(16)对车速v求导得

(17)

2 两难区控制策略

2.1 两难区黄灯控制策略

黄灯时间的合理设置可显著减少车辆陷入两难区的概率[9]，提高交叉口的安全性和车辆的通行效率.

2.1.1 国外黄灯时间设置

1)美国交通工程师协会的交通工程师手册推荐的黄灯时间计算公式为

(18)

式中：Y为黄灯时间(s);τ为驾驶员反应时间，取1s；v为车辆进入交叉口的速度(m/s)；G为重力加速度，取9.8m/s2；g为坡度(%)；d为制动减速度，这里取定值3.05m/s2.

2)日本交通工程师协会的交通信号控制手册中推荐黄灯时间计算公式为

(19)

式中：Y为黄灯时间(s)；τ为驾驶员反应时间取0.7s；v为车辆进入交叉口的速度(m/s)；d为制动减速度，这里取定值3m/s2.

3)德国交通信号控制规范要求黄灯时间的计算公式为

(20)

式中：Y为黄灯时间(s)，一般取最小值;τ为驾驶员反应时间取1s;v为车辆进入交叉口的速度(m/s);d为制动减速度，这里取定值3.5m/s2.

2.1.2 针对陷入两难区车辆的理想黄灯时间设置

当DZ≤0时，车辆不管在什么位置，都不存在两难区，只有选择区，该黄灯时间计算公式为

(21)

参照图7黄灯时间与两难区的关系，考虑到黄灯时间设置太长会影响交叉口通行效率，可将DZ=0所对应的黄灯时间作为不存在两难区的理想黄灯时间设置.此时该车辆在交叉口处不存在两难区，也就没有陷入两难区的可能性，不过单凭此式计算出来的黄灯时间值偏大，交叉口前后车辆容易因为对黄灯时间的错误判断而发生追尾事故，影响交叉口通行效率.

2.1.3 针对陷入两难区车辆的黄灯时间控制策略

本文采用黄灯时间由小到大循环判断的预测方法.由于两难区域长度随着黄灯时间的增大而减小，则先将黄灯时间Ty设为1s，以Ty=Ty+1进行循环判断.该策略可在安装有无线通信ZIGBEE技术的信号灯监测系统中实现.

首先对某一辆车进行判断，当黄灯启亮时，系统检测出驾驶员反应时间Tr和此刻车辆所处的位置即到停止线的距离S1，车速v、黄灯时间Ty(开始为1s)，由公式(9)计算出DZ的值.若DZ≤0，由图5可知车辆在任何位置都不会处在两难区，则输出黄灯时间Ty.反之，若DZ>0，由图4可知且车辆到停止线的距离不在L1≤S1≤L2范围内，则车辆不会处在两难区，输出黄灯时间Ty；如果车辆到停止线的距离满足L1≤S1≤L2，车辆会处于两难区，需进行Ty=Ty+1重新判断，直至输出黄灯时间Ty.

再根据各车辆对应的黄灯时间Ty对其进行修正，将黄灯时间最大设为5s，则解决两难区最佳黄灯时间为

(22)

黄灯时间控制策略流程图如图8所示.

图8　黄灯时间控制策略

2.2 两难区车载控制策略

根据黄灯启亮时车辆的加减速情况，提出车辆加速和减速不同情况下的两难区车载预警控制策略.该策略可在安装有GPS和无线通信ZIGBEE技术的车载系统中实现.

黄灯启亮时，系统收集各车辆交叉口控制参数：驾驶员反应时间Tr和此刻车辆所处的位置即到停止线的距离S1，车速vi、车辆最大加速度a0，从信号灯监测中心发出的黄灯时间Ty，由公式(9)计算出DZ的值.

2.2.1 车辆加速状态下的车载控制策略

黄灯启亮时，若车辆加速度大于等于0，当求出DZ=0，L1=L2(如图6所示)，且车辆距离停止线恰好为L1时，则提示驾驶员既可在红灯启亮前安全停靠于停车线前又可在红灯启亮前不超速顺利通过交叉口.

当求出DZ>0(如图4所示)时，如果车辆离停止线的距离小于L2，则应该提醒驾驶员在红灯启亮前不超速顺利通过交叉口；如果车辆离停止线的距离大于L1，则应该提醒驾驶员减速制动在红灯启亮前将车停靠于停止线前；如果车辆离停止线的距离在L1和L2之间，则车辆在红灯启亮前既不能安全停靠于停止线前又不能在不超速的情况下通过交叉口，说明车辆已陷入两难区，此时信号灯监测系统将进行黄灯时间控制，提醒驾驶员注意行车安全，避免追尾和碰撞.

当求出DZ<0(如图5所示)时，如果车辆离停止线的距离小于L1，则应该提醒驾驶员可在红灯启亮前不超速通过交叉口；如果车辆离停止线的距离大于L2，则应该提醒驾驶员减速制动，在红灯启亮前将车停靠于停止线前；如果车辆离停止线的距离在L1和L2之间，则车辆在红灯启亮前既可以安全停靠于停止线前又可在不超速的情况下通过交叉口，说明车辆处于选择区，提醒驾驶员随意选择停或行.

2.2.2 车辆减速状态下的车载控制策略

2.2.3 针对陷入两难区车辆的车载控制策略

图9为车载预警系统控制示意图，图9中各量含义如下：A——不提示，B——提示可以此交叉口最大限速通过交叉口，C——提示减速停车，D——车辆陷入两难区，提示黄灯时间将延长，E——提示可以此速度通过交叉口，F——可以此减速度停车，G——提示加大制动力度停车.

图9　车载预警系统控制示意图

3 结论

(1)本文两难区数学模型体现车速时变动态特性，且车辆最大减速度和最大加速度参数没有定义标准和推荐值，均以实际每一辆车的真实参数进行两难区预测.

(2)对两难区长度影响因素分析可知：当DZ≤0时不存在两难区，且DZ值越小，处于选择区的可能性越大，越能提高交叉口的通行效率和安全性.

(3)两难区长度DZ随着驾驶员反应时间Tr的增大而增大；随着车辆加速度a的增大而减小；随着黄灯时间Ty的增大而减小；当黄灯时间一定时，可以找到使两难区域长度最小的车速；当车速一定时，

随着黄灯时间的增加，DZ值急剧下降，可以找到满足DZ=0的黄灯时间.

(4)根据黄灯启亮时车辆实际加减速情况，选用相应的两难区车载预警控制策略.

(5)在以往解决两难区黄灯时间问题上，黄灯时间通过DZ=0计算得出，忽略了DZ>0时车辆也有不在两难区的可能性，本文黄灯时间的设置通过Ty=Ty+1循环判断DZ>0时车辆是否不在两难区，该法可使求出的黄灯时间显著变小，更能提高交叉口的通行效率.

(6)本文主要针对交叉口直行车辆进行分析，对于处于左转弯待转区的车辆，由于停止线向前延伸，通过交叉口的直径W变短，陷入两难区的概率很低，故不做研究.但对于直行车道区来说，如果也将停止线向前延伸一段距离，该方法是否能够解决两难区问题也将是需要深入研究的.

参考文献：

[1]张存保, 陈超, 严新平. 车路协同下信号控制交叉口两难区问题改善方法[J]. 中国安全科学学报, 2012, 22(6): 86-91.

[2]王金梅, 王兆安, 邓雯, 等. 与闯红灯违规相关的困境区域的研究[J]. 西安交通大学学报, 2005, 39(2): 205-209.

[3]黄玮, 金向东, 马万经. 信号控制交叉口两难区控制问题初探[C]// 2008 第四届智能交通年会论文集. 青岛: 全国智能运输系统协调指导小组, 2008: 317-322.

[4]CarrollJM,SrinivasaRS,HassanAC.Designandinstallationguidelinesforadvancewarningsystemsforend-of-greenphaseathighspeedtrafficsignals[R].Texas:TransportationInstitute, 2003.

[5]钱洪波, 韩皓. 再论道路交叉口信号控制中黄灯信号问题[J]. 交通信息与安全, 2012, 30(5): 94-101.

[6]GazisD,HermanR,MaradudinA.Theproblemoftheambersignallightintrafficflow[J].OperationsResearch, 1960, 8(1): 112-132.

[7]PanagiotisP.DriverbehaviordilemmazoneandsafetyeffectsaturbansignalizedintersectionsinGreece[J].AccidentAnalysisandPrevention, 2007(39): 147-158.

[8]OlsonP,RotheryR.Decelerationlevelsandclearancetimesassociatedwiththeamberphaseoftrafficsignals[J].TrafficEngineering, 1972, 42(4): 16-19.

[9]SheffiY,MahmassaniH.Amodelofdriverbehaviorathigh-speedsignalizedintersections[J].TransportationScience, 1981, 15(1): 50-61.

(编辑：郝秀清)

收稿日期：2014-09-07

作者简介：刘润乔，男，liurunqiaol@163.com; 通信作者：韩加蓬，男，hjpsdlgdx@sdut.edu.cn

文章编号：1672-6197(2015)02-0051-06

中图分类号：TH137

文献标志码：A

Influencingfactorsandcontrolstrategiesofdilemmazone

LIURun-qiao,HANJia-peng,LIUHong-guang

(SchoolofTransportationandVehicleEngineering,ShandongUniversityofTechnology,Zibo255049,China)

Abstract:The vehicle dilemma zone length range had been got through the dilemma zone model where the speed was changedfrom moment to moment. Thedilemma zone effect relationshipwas analyzedin the aspectsof yellow light time, vehicle's acceleration and deceleration, vehicle speed, and reaction time. According to the vehicle's acceleration and deceleration conditions, using the prediction methods of amberlightstime to cycle judgment, dilemma zone amberlightstime control strategy and vehicle warning control strategywereproposed. Thesestrategies could reduce theincidence of being involved inthe dilemma zone events,and decrease the traffic accidents.

Key words:speed variable; vehicle warning; prediction of amberlight time; influencing factorsof the dilemma zone