一类三次系统的大同宿分支

尚德生, 周运明， 周爱华

(山东理工大学 理学院， 山东淄博255049)

一类三次系统的大同宿分支

尚德生, 周运明， 周爱华

(山东理工大学 理学院， 山东淄博255049)

摘要：利用多参数摄动理论和微分方程定性理论，通过对一类三次系统扰动形成的大同宿轨研究，得到该系统至少有5个极限环，并给出极限环的分布为3+(1,1)分布.

关键词：摄动； 分支； 三次系统； 极限环； 大同宿轨

1引言与主要结论

文献[1]研究了下面的 Liénard系统

(1)

证明了对ε的解析函数a1,a2,a3，且|ε|充分小时系统至多存在三个极限环。文献[2]又研究了系统

(2)

发现系统可以有四个极限环。文献[3]又进一步讨论下面的三次系统

(3)

其中f2(x,y)=a1+a2x+a3x2+a4y2.单纯地通过对同宿轨和双同宿轨的扰动进行研究得到系统(3)可以有五个极限环，其分布为 1+(2, 2)的结构.

首先利用对双同宿轨扰动得到一个大的同宿轨，然后再研究大同宿轨的稳定性，并利用改变大同宿轨的稳定性的方法进行研究，得到系统(3)仍然可以有5个极限环，但是得到一种新的分布3+(1,1)(即在三个大极限环里面包含两个分离的小极限环)，这种分布是文献[3]中没有的. 以定理形式给出.

定理 1 系统 (3)至少可以有5个极限环，其分布是 3+(1，1).

注：利用扰动大同宿轨研究极限环的方法已经在文献[4]中运用，在这里利用这一方法来讨论另外一个不同的多项式系统.

2扰动大同宿轨及引理

由于未扰动系统是Hamilton的，其Hamilton函数为

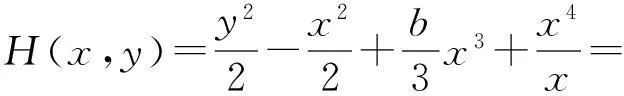
而H(x,y)=0对应未扰动系统的双同宿轨，记为

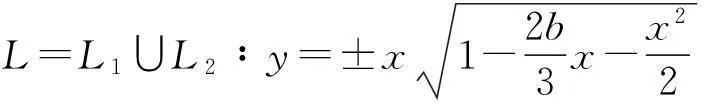
x1≤x≤0,或0≤x≤x2,其中

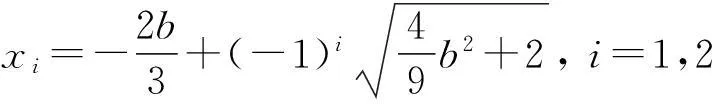
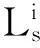
其中

Mi(a)=-∮Li(a1+a2x+a3x2+a4y2)ydx=

2[Ai1a1+Ai2a2+Ai3a3+Ai4a4],i=1,2

(4)

根据文献[3]的计算得

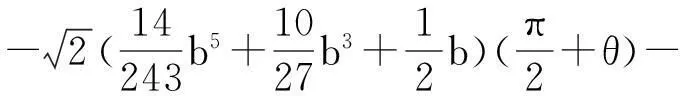
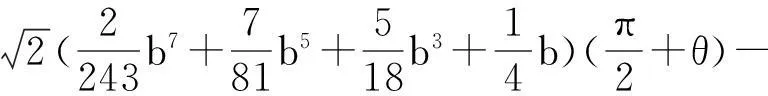
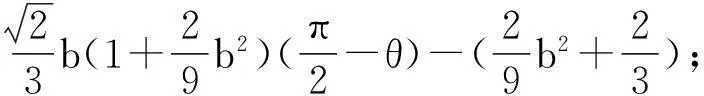
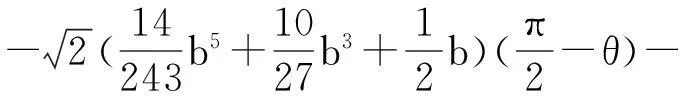
显然，有下述引理成立

引理 1如果b>0，则存在函数

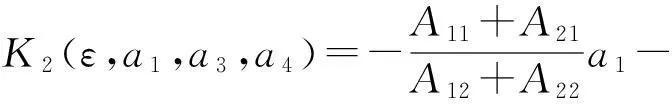
(5)

附近有一个大同宿轨Γ*存在的充分必要条件是

a2=K2(ε,a1,a3,a4),即d1+d2=0

且d1≠0.对于d1>0及d1<0的情况分别见图1(a)、(b).

图1　当d1+d2=0而d1=0时形成的大同宿轨

由于系统(3)在原点扰动下的散度为

div(3)|Oε(0,0)=-εa1+O(ε2),

可得下面的引理成立

引理 2存在函数

K1(ε,a3,a4)=O(ε)

(6)

使得div(3)|Oε(0,0)≥0(<0)当且仅当

a1≤(>)K1(ε,a3,a4).

引理 3 (Ⅰ)如果ai=Ki,i=1,2成立，则当t→±∞时，积分

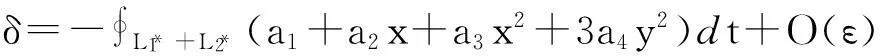
δ=-∮L1+L2(a1+a2x+a3x2+3a4y2)dt+O(ε).

(Ⅱ)当δ>0(<0)时，大同宿轨Γ*是不稳定(稳定)的.

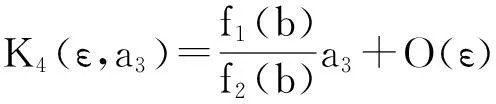
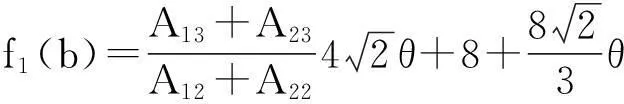
证明 (Ⅰ) (Ⅱ)的证明见文献[5-6]. 对于(Ⅲ)的证明，结合文献[2-3]中的计算，得到

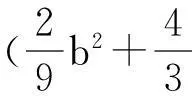
从而在 ai=Ki,i=1,2的条件下有

δ=δ10(b)+δ20(b)=

a3f1(b)+a4f2(b)+O(ε),

其中

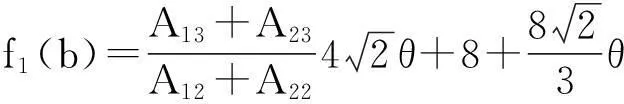
a4≥(<)K4(ε,a3)

(7)

这可以通过化简并利用Mathematica7.0得到结论(注意：当 b>0时，有f2(b)>0).

根据文献[6-7]的方法和公式计算在条件 ai=Ki,i=1,2,4下系统关于大同宿轨Γ*的一阶鞍点量. 为了便于理解，重述主要结果如下：

对于形如

的系统，在原点处的一阶鞍点量 R11有下面的计算公式

[fxy(fyy-fxx)+gxy(gyy-gxx)-

fxxgxx+fyygyy]/λ}

这里各函数的导数都是计算其在原点处的值(详见文献[7]).

根据该公式易求得系统对应大同宿轨Γ*处的一阶鞍点量为

R11=(3a4-ba2-a3)ε.

引理 4在条件ai=Ki,i=1,2,4下，当a3ε>0时，大同宿轨Γ*处的一阶鞍点量

R11=-4Ma3ε+O(ε2)<0，

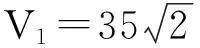
且

s1=529659+379053b2+111510b4+

18060b6+1400b8,

s2=395118+1125819b2+768744b4+

244440b6+40320b8+2800b10,

s3=59049+41553b2+1662606b4+

1524744b6+544320b8+89040b10+5600b12,

17199b2+7980b4+980b6)θ+140b3(9+2b2)θ2

根据文献[6]可以得到下面的结果

引理 5 如果大同宿轨Γ*为顺时针定向的，且一阶鞍点量R11>0(<0)，则大同宿轨Γ*为外不稳定 (稳定)的.

3焦点的稳定性

下面讨论在条件(5)-(7)下，焦点Piε(xi0+O(ε),O(ε)),i=1,2的稳定性问题，其中

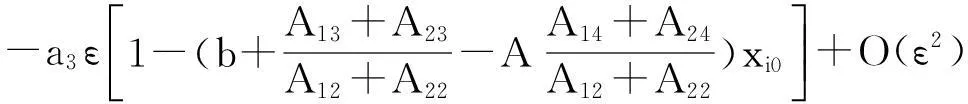
这样对于奇点Piε,i=1,2处，可以先不考虑前面的-a3ε，利用数学软件Mathematica7.0分别画出其在b>0部分的图像，如图2所示.

图2　扰动后焦点Piε的图像(其中-εa3<0固定)

且可得图像的两个零点b1≈0.379626，b2≈5.03778. 这样根据图像和-a3ε的符号可得到表1.

表1　系统(3)在两焦点Piε,i=1,2处对于

根据文献[5-6]得到引理6:

引理6当div(Piε)<0(相应地>0)时，焦点div(Piε)是稳定(相应地不稳定的).

4系统的环性分析及定理证明

下面在ε>0充分小且a3>0固定的条件下完成定理1的证明和系统分析.

对于d1+d2=0，且d1>0的情形，根据上述表1及引理6，得到对于b∈(0,b1)的情形，焦点P1ε是不稳定的，而P2ε是稳定的. 这样根据图1(b)的大同宿轨内剩余的两条稳定和不稳定流形走向，可知在大同宿环内各有一个小的极限环出现，它们分别围绕P1ε和P2ε；对于b∈(b1,b2)，由于焦点Piε,i=1,2都是稳定的，故而在大同宿轨内仅有一个小的不稳定极限环出现，它围绕P2ε；而对于b∈(b2,+∞)，情形与 b∈(0,b1)时完全相同，在大同宿轨内也各有一个小环分别围绕P1ε和 P2ε.

由于R11<0，根据引理5得到大同宿轨是稳定的，这样对于固定的a3>0，如果|a4-K4| ≪a3，且a4>K4，则有δ>0，根据引理4知道大同宿轨这时改变稳定性，即由稳定变成不稳定，可以根据环域定理得到在大同宿轨外有一个稳定的大极限环Γ1,s出现；然后对固定的a3,a4，让|a1-K1|≪|a4-K4|≪a3，且a1>K1，这时大同宿轨再次改变稳定性，即由不稳定变成稳定，又可以在大同宿轨外，在Γ1,s内出现一个不稳定的大极限环Γ2,u；最后，对于固定的a1,a3,a4，如果|a2-K2|≪|a1-K1|≪|a4-K4|≪a3，且a2>K2，则大同宿轨破裂，同时原大同宿轨的不稳定流形在稳定流形的外面，从而又有一个稳定的大极限环 Γ3,s出现在Γ2,u内部. 这样系统(3)在这种情况下会出现3个大极限环套着左右各一个小极限环的现象，记为3+(1,1)(如图3所示).

图3　五个极限环的3+(1,1)分布

其它情形可以类似讨论，而出现极限环的个数及分布分别如下：

当d1>0时,若b∈(b1,b2),则为3+(0,1)分布；若b∈(b2,+∞),则为3+(1,1)分布.当d1<0时，若b∈(0,b1),则为3+(0，0)分布;若b∈(b1,b2),则为3+(1,0)分布；若b∈(b2,+∞),则为3+(0,0)分布.

这样，通过先设定参数使得未扰动系统原先的两个同宿轨同时破裂并产生一个大同宿轨，然后来研究大同宿轨的稳定性，并通过适当扰动来改变大同宿轨的稳定性，在最后改变参数值让大同宿轨按照预定的要求破裂的方法，得到系统(3)可以出现5个极限环，其分布为3+(1,1)，定理1得证.

注：在该类扰动下系统解的有界性判断比较困难，所以不能判断在Γ1,s的外围是否还有大极限环存在，所以根据我们的方法得到系统(3)可以存在 3+(1,1)分布的至少5个极限环的结论.

参考文献:

[1]IlieveID,PerkoIM.Higherorderbifurcationsoflimitcycles[J].JournalofDifferentialEquations,1999, 154: 339-363.

[2]韩茂安. 一类三次系统极限环的个数与分布[J]. 数学年刊，2002, 23A(2): 143-152.

[3]ShangDS,HanMA,SunJP.Theglobalbifurcationofacubicsystem[J]. 应用数学学报(英文版), 2006，22(2):325-332.

[4]ShangDS.ThelargeHomoclinic-loopbifurcationofakindofcubicsystem[J]. 数学进展, 2009，38(6): 755-760.

[5]韩茂安，陈健. 双同宿分支中极限环的个数[J]. 中国科学, 2000, 30A(5): 401-414.

[6]韩茂安. 动力系统的周期解与分支理论[M]. 北京：科学出版社, 2002，287-332.

[7]HanMA,ZhangTH.Somebifurcationmethodsoffindinglimitcycles[J].MathematicalBiosciencesandEngineering(英文版),2006,3(1):67-77.

(编辑：刘宝江)

收稿日期：2014-09-09

作者简介：尚德生，男，sdsshang@163.com

文章编号：1672-6197(2015)02-0027-05

中图分类号：O175.12

文献标志码：A

The large Homoclinic loop bifurcation of a kind of cubic system

SHANG De-sheng, ZHOU Yun-ming， ZHOU Ai-hua

(School of Science, Shandong University of Technology， Zibo 255049, China)

Abstract:In this paper, the bifurcations of a large homoclinic loop, which obtained by perturbing a kind of cubic system, are considered. Through applying the bifurcation theory of planar dynamical systems, we obtain that the given system can have at least five limit cycles, and the distributions of the limit cycles are 3+(1, 1).

Key words:perturbation; bifurcation; cubic system; limit cycle; large Homoclinic loop