一种适于GEO卫星姿轨控结合的正常模式东西控制方法

胡文静，聂琨坤，王学梅

（北京空间信息中继传输技术研究中心，北京 100094）

0 引言

GEO卫星在轨始终受地球形状摄动、日月摄动、太阳光压摄动等三种主要摄动力的作用，在东西（经度）、南北（纬度）方向漂移。定点位置保持就是克服这三种摄动的影响，使卫星始终保持在定点位置东西和南北方向误差在保持环范围内。在GEO卫星的东西位置保持控制过程中，通过安装在星上的10N推力器产生向东或向西的作用力，完成平经度和偏心率的协同控制。文献［1-2］对GEO通信卫星位置保持原理及实施策略进行了阐述；文献［3］提出了一种偏置动量卫星东西位置保持策略优化方法，可有效延长东西位置保持周期；文献［4］提出了GEO卫星连续式等间隔脉冲推力东西位置保持策略，可长期有效地控制卫星平经度在漂移环范围内，利于控制过程的组织实施。

某DFH-3平台GEO卫星（以下简称A星）正常模式东西位置保持控制时，使用动量轮作为主要的控制器件。因东西向安装的推力器存在不对称性，为确保控制期间动量轮转速、转速差保持在正常值范围内，采取先进行动量轮转速控制而后进行正式点火的控制策略。其直接影响是：每次东西控制时间变长，整个控制时长约3h，其中动量轮转速控制近2h，正式点火1h多；控制效率低，位保点火过程中因姿态或动量轮转速超限而多次暂停控制，东西控制量并不大，但点火时间耗费1h。

为提高控制效率，缩短控制时间，同时尽量减少手动操作，需对控制过程进行改进，研究更高效、可靠的控制实施方法。本文对一种适于GEO卫星姿轨控结合的正常模式东西控制方法进行了研究。

1 原因分析

1.1 东西位置保持原理

由于地球是不规则的扁球体，产生的切向摄动使GEO卫星星下点在东西向漂移。为保持卫星的定点精度，须进行东西方向的位置保持，一般将星下点控制在定点位置保持环范围内。在实施东西位置保持期间，由于采用对称推力器产生X向速度，改变卫星轨道半长轴，从而改变卫星星下点。东西位置保持的控制要素包括经度、半长轴和偏心率，通过设计合适的保持环控制这些要素。如图1所示，保持环的横坐标为经度差，纵坐标为半长轴与同步轨道半径差，在漂移加速度作用下，卫星由保持环左下方的初始位置点A向西漂移至点B后逐渐返回漂移至点C，在C处进行位置保持，降低半长轴至点A，重复新一轮漂移周期。东西保持环可分成以下区域：

a）轨道漂移率控制所需的保持环半宽度Δld（3区）；

b）轨道偏心率造成的平经度日振荡Δle（2区）；

c）轨道确定、轨道／姿态控制及短周期项摄动造成的平经度误差Δlm（1区）。

东西位置保持控制主要通过控制星上推力器产生向西或向东的推力脉冲，其总的效果是完成平经度、平经度漂移率和偏心率的控制。在东西位置保持实施前，要精确测轨定轨，以计算准确的位置保持控制参数（主要包括推力器选择，工作脉宽、周期和次数，点火启控时刻及偏航确定系数等）；在位置保持期间，因卫星成对推力器的推力差别、推力偏斜及安装误差等形成对星体的干扰力矩，故在每次东西位保控制后，应计算位保控制时的干扰力矩，并在下次同类型（姿控模式、推力方向、推进分支、关调制占空比等相同）轨控中予以补偿；轨控结束后，也应进行精确测轨定轨，对轨控推力和干扰力矩进行标定。但对DFH-3平台的三轴稳定卫星，正常模式下进行东西位置保持控制时，推力器并不参与卫星姿态控制，动量轮是主要的姿控设备。

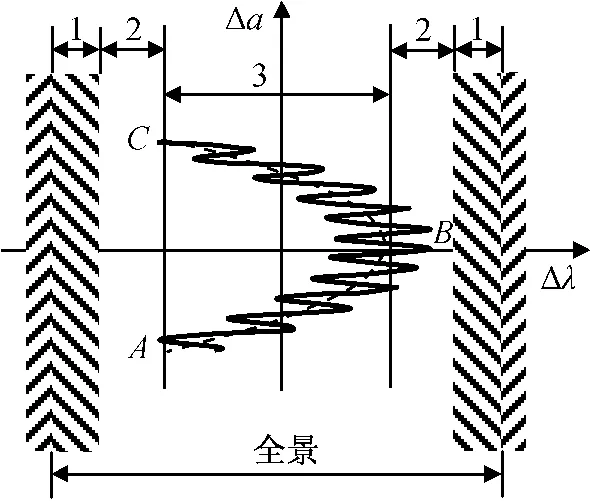
图1 东西方向位置误差分配Fig.1 V-configuration wheels fixing

1.2 动量轮姿态控制原理

动量轮三轴姿态稳定系统工作原理基于动量矩守恒，即卫星的总动量矩矢量对时间的导数等于作用在卫星上外力矩矢量之和［5］。因动量轮是以内力矩作为控制力矩，故当外力矩矢量之和为零时，卫星总动量矩守恒。通过改变动量轮的动量矩矢量，就可吸收卫星多余的动量矩，从而实现对姿态的控制。

A星安装的V型动量轮，构型结构如图2所示。动量轮1（MW1）和动量轮2（MW2）为角动量相同的偏置动量轮（RW）在y-z平面构成V型安装，每个轮子角动量与－y轴的夹角均为β，另一个备份反作用轮RW安装在z轴上。该构型提供了偏置角动量三种组合模式：主份工作模式，MW1，MW2组成V型；＋L型备份，MW1，RW组成；－L型备份，MW2，RW组成。当 MW1或 MW2失效时，可切换至＋L型或－L型备份模式，可靠性较高［6］。通过力矩分配，V，L型轮在俯仰轴和偏航轴上均能产生连续的控制力矩分量，分别控制卫星俯仰姿态、滚动姿态。正常模式下，A星姿态控制采用轮控和角动量管理结合的方法。V型动量轮主份工作时，将控制动量方向设置在偏航轴上，以获得较好的滚动控制精度。当有俯仰姿态误差时，可用地敏测量，通过由MW1，MW2在－y轴上合成的角动量附近同时增加或减小转速，实现俯仰姿态的连续控制。

图2 单自由度V型偏置动量系统构型Fig.2 V-configuration wheels fixing with single freedoom

A星滚动控制为角动量控制，通过调整动量轮在偏航轴上的角动量大小控制卫星的滚动姿态角。滚动控制器先根据敏感器测量值给出控制角动量，再基于动量轮的偏航角动量测量值，将控制角动量转换为滚动控制力矩，然后与俯仰控制力矩经力矩分配计算，获得每个动量轮的控制力矩电压。

定性分析滚动轮控变化时，不考虑章动时有简化角动量公式

Hz＝－Hyφ＋hz. （1）

式中：Hz为偏航轴角动量；Hy为俯仰轴动量偏置；φ为滚动角；hz为动量轮在偏航轴向产生的角动量变化量。A星进行东西位置保持时，由推力器2、3共同喷气，推力器2产生＋X、－Z向力矩，推力器3产生＋X、＋Z向力矩。理论上，推力器2、3同时点火时偏航方向力矩应相互抵消，但由于推力器2、3喷气效率、安装角度不同，造成了Z向力矩不均衡，形成偏航方向的干扰力矩。对A星来说，推力器3产生＋Z向的力矩要大于推力器2产生的－Z向力矩。当干扰力矩使姿态发生正向滚动偏差（φ＞0）时，动量装置应在偏航轴的负方向产生角动量变化量（hz＜0），以吸收扰动角动量。上述状态对MW1、MW2转速影响的直接结果为：MW1的转速减小，MW2的转速增大，两动量轮转速差增大。

因此，在东西控制前先控制动量轮转速至标称转速，再将动量轮1的转速控制到下限转速附近，将动量轮2的转速控制到上限转速附近，如图3所示。控制期间动量轮转速差变化最大达到1 200r／min。

1.3 正常模式东西控制流程

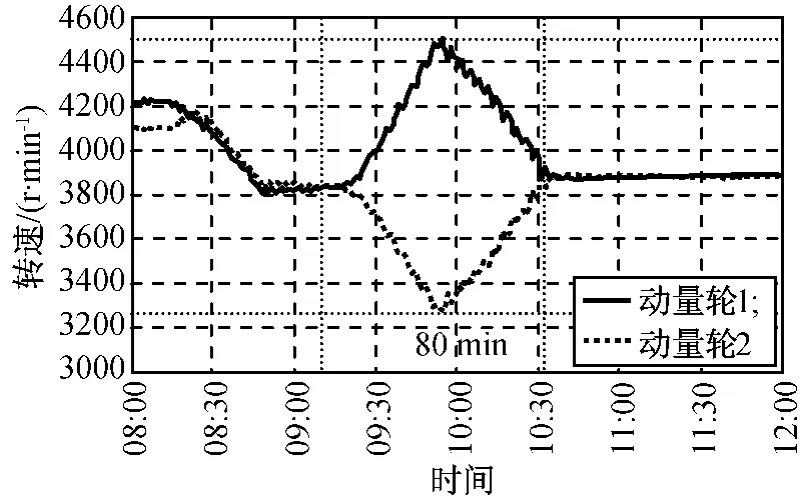
图3 东西控制期间动量轮转速Fig.3 Rotation rate change of momentum wheel during east-west maneuver

实际长常模式东西位置保持卫星控制时，正式点火开始后，需根据卫星姿态和动量轮转速的变化控制卫星点火进度。正常模式下，使用偏置动量轮进行卫星姿态控制，如卫星姿态超过正常模式姿控门限、动量轮转速超出正常范围内时，应立即停止推力器点火，否则可能造成卫星姿态异常。正常模式东西控制流程如图4所示。

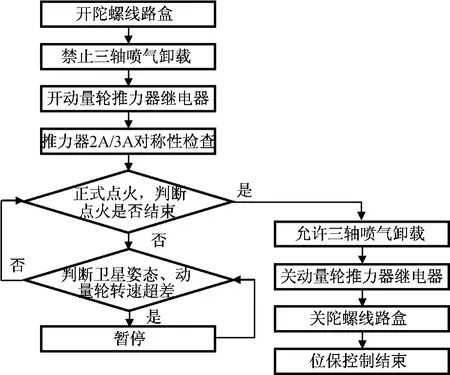
图4 改进前正常模式东西控制流程Fig.4 Formal flowchart of normal mode east-west maneuver

实际控制期间星上地敏俯仰角、滚动角如图5所示。因轨控期间推力器的不对称性，卫星姿态变化较明显，滚动角在（－0.38°～0.51°）范围内变化，控制过程中不得不暂停点火过程，待卫星姿态稳定后再继续点火控制。因此，造成了实际点火时间较长（约80min）。

2 姿轨控结合东西控制方法

图5 东西控制期间滚动和俯仰角Fig.5 Rolling angle and pitching angle during east-west maneuver

由于2A／3A推力器存在不对称性，根据A星的在轨管理经验，为避免姿态出现超差，位保点火过程中通常需进行一定的姿态控制。参考干扰力矩估计与补偿计算结果，推力器标定系数为0.91，因此是采用5∶1的比例关系交替进行轨道和姿态控制：每进行5次推力器2、3点火，进行1次推力器2点火。为提高控制效率，缩短控制时间，同时也尽量减少手动操作，采取5次推力器2、3位保点火后，实施1次2A点火动量轮转速控制，以便更好地控制卫星姿态及动量轮转速变化，减少在位保点火过程中因姿态或动量轮转速超限而暂停的次数。轨控和姿控结合的正常模式东西位置保持卫星控制流程如图6所示。

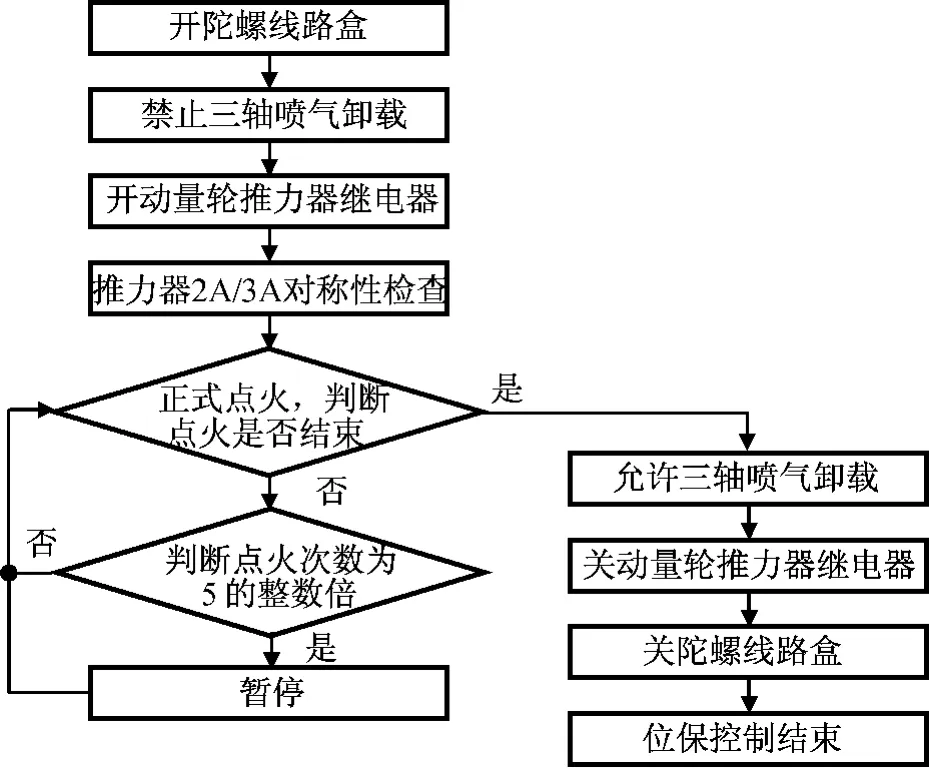
图6 姿控和轨控结合的东西控制流程Fig.6 Flowchart of attitude control and orbit control east-west maneuver

为比较在改进东西控制方法前后的控制效率，同样在正常模式下，对A星实施东西位置保持控制。为确保东西控制期间动量轮转速、转速差保持在正常值范围内，在控前用时0.5h实施动量轮转速控制，将动量轮控制到标称转速左右。正式控制开始后，按轨控和姿控相结合的控制策略，进行5次2A／3A位保点火后，进行1次2A点火实施动量轮转速控制，以更好地自动控制卫星姿态及动量轮转速变化，减少在位保点火过程中因姿态或动量轮转速超限而暂停的次数。

东西位保控制期间星上地敏俯仰角和滚动角如图7所示。由图可知：卫星姿态角变化范围为－0.23°～0.1°，满足正常模式姿控要求。控制过程中动量轮转速如图8所示。由图可知：因控制过程中采用了轨控与姿控结合的控制策略，2A推力器的单独点火补偿了推力器不对称性引起的动量轮转速变化，控制过程中动量轮转速差变化约400r／min；控制结束后，动量轮转速保持在标称转速附近。点火期间，卫星姿态稳定、动量轮转速未超限，实际控制的整个正式点火过程耗时约30min。

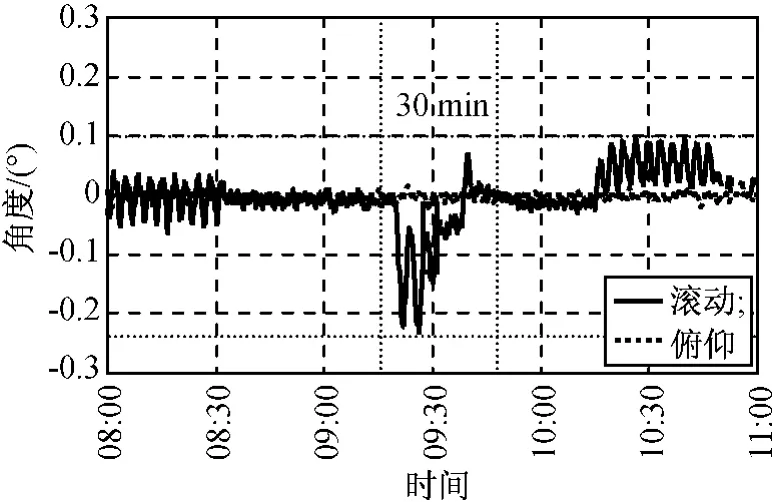
图7 东西控制期间滚动和俯仰角Fig.7 Rolling angle and pitching angle during east-west maneuver

图8 东西控制期间动量轮转速变化Fig.8 Rotation rate of momentum wheel during east-west maneuver

3 结束语

本文基于实际东西控制效率低的原因分析，提出了在轨控过程中进行角动量主动补偿控制（即姿轨控结合的东西控制）方法，并在实际任务中得到了验证。结果表明：该法减小了控制过程中姿态及动量轮转速变化，显著减少了控制时间。这种控制方法可推广应用到推力器对称性较差的GEO卫星正常模式下东西位置保持控制中。

［1］ 李于衡.地球静止轨道通信卫星位置保持原理及实施策略［J］.飞行器测控学报，2003，22（4）：53-61.

［2］ 李于衡，刘宁宁.在轨跟踪与数据中继卫星测控关键技术（上）［J］.上海航天，2006，23（4）：1-7.

［3］ 陈 宏，郑 军，李于衡.偏置动量卫星东西位置保持策略优化方法［J］.上海航天，2011，28（3）：37-41.

［4］ 常建松，李全军，袁 勇.静止轨道卫星连续式等间隔脉冲推力东西位置保持策略［J］.空间控制技术与应用，2013，39（2）：53-57.

［5］ 周 军.航天器控制原理［M］.西安：西北工业大学出版社，2001.

［6］ 屠善澄.卫星姿态动力学与控制（2）［M］.北京：中国宇航出版社，1998.