折叠变换媒质散射特性与参数分析

庞旭东，朱伟华，朱守正

（1.上海机电工程研究所，上海 201109；2.华东师范大学 信息科学与技术学院，上海 200241）

0 引言

变换电磁学利用坐标变换的方法，可根据需要设计特定本构参数（介电常数ε，磁导率μ）的介质，使电磁波在这些介质中以期望的方式传播或散射，从而达到对电磁波的操控，结合超材料技术，可设计多种新颖器件［1－3］。早期的应用是电磁隐身斗篷，其后发展出了多种不同的坐标变换方式（如折叠变换），以及其他功能的变换电磁学器件（如电磁波集中器、电磁波扩展器和电磁波旋转器等）［4－9］。

电磁波集中器／聚焦器对入射电磁波有汇聚作用，并可放大此器件内部物体的散射，这些性能类似光学器件中凸透镜的功能，而应用频段则拓展至电磁波谱领域［6－11］。电磁波集中器可分为普通型和折叠变换式两类。目前对这两类器件的研究缺乏统一性，对后者的研究相对更少。少量文献对集中器散射放大作用研究，但对折叠变换媒质散射放大特性的定量对比分析尚不深入［11］。折叠变换式集中器的媒质参数多为负值，目前暂未有文献对其参数详细分析。本文对折叠变换式集中器变换媒质的散射特性进行了仿真验证与计算。

1 理论基础

上述两类电磁波集中器的坐标变换函数均为折线型分段函数［6－9］。对折叠变换式集中器二维圆柱模型，在柱面波照射，波源频率f＝3GHz，波源距离d＝0.9m，a＝0.1m，b＝0.2m，k＝3条件下，用Comsol Mutiphysics有限元法分析软件仿真，结果如图1（a）所示［6］。其中：内圆r＝a为器件的内边界；外圆r＝b为器件的外边界；k为倍率。两者的对比如图1（b）所示。采用圆柱坐标系，原始空间和变换空间分别为（r，θ，z），（r′，θ′，z′）。此处：r，θ，z分别为各自空间径向分量、角度分量和轴向分量。

图1（b）中：r为原始空间圆柱半径；纵轴r′为变换空间圆柱半径；折线1、2分别为普通电磁波集中器和折叠变换式集中器的坐标变换函数。折线2表示将0≤r≤s区域压缩到0≤r′≤a（s＞b），s≥r≥b区域被变换到a≤r′≤b，且b≤r≤s区域被翻折回b≤r′≤s。其中带有局部空间的翻折，是一种折叠变换，称其变换媒质为折叠变换媒质或互补媒质，参数多为负值［5］。折线1中a＜s＜b，表示普通型集中器／聚焦器［6－9］。坐标变换函数中s的不同取值可得到两种不同器件。

图1 仿真与对比Fig.1 Simulation and comparison

器件的坐标变换公式可统一表示为

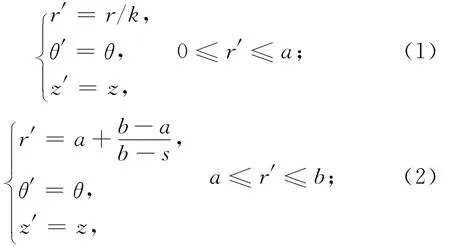
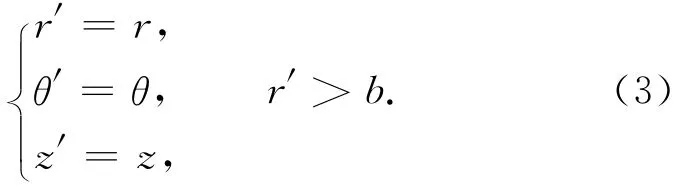
式中：s＝ka［6－9］。折线1、2的s值范围不同，故普通型集中器1＜k＜b／a，折叠变换式集中器k＞b／a。对图1的模型b／a＝2，普通型集中器的k只能限制为小于2；折叠变换式集中器的k可大于2，甚至更高，其媒质参数也会出现负值。

令sinθ＝y／r，cosθ＝x／r，折叠变换式集中器柱坐标系中介电常数ε各分量可表示为

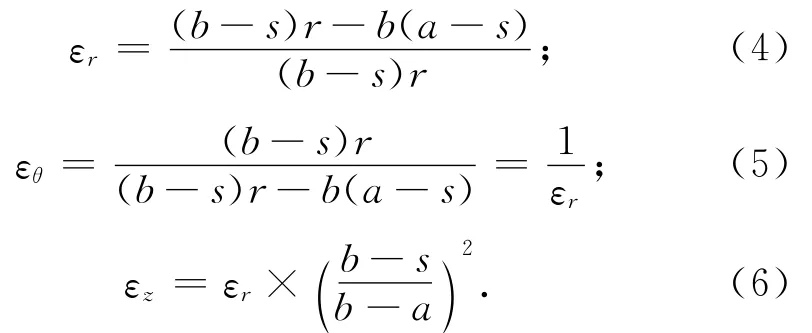
介电常数ε张量在x、y向分量可表示为

2 散射特性

由图1（a）可知：与普通型集中器类似，折叠变换式集中器对入射波也有汇聚作用，具电磁散射放大功能，相当于电磁波谱领域的凸透镜［5－9］。倍率为k的集中器，对内置物体的散射尺寸，其放大倍数为k。折叠变换式集中器的倍率k＞b／a，可突破器件尺寸的限制，实现较高倍率的散射放大作用。

本文用数值仿真计算验证折叠变换式集中器的散射特性。在图1（a）器件模型内部放置一较小尺寸物体的模型，用平面波照射得到散射模式的仿真结果。本文选取F－22隐形飞机截面形状的二维仿真模型（实际飞机的共形缩比模型）作为内置物体，模型机身长度h＝0.134 6m，模型翼展宽度w＝0.10m。对飞行体，本文设置仿真模型的边界为金属，器件尺寸a＝0.1m，b＝0.2m。对各种模型散射模式的仿真结果，分别定量计算其散射宽度值［10］。因有限元法计算的结果是近场数据，故还需由Huygens原理将近场数据转为远场数据，再计算散射宽度

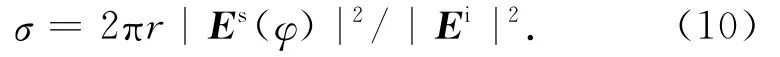
式中：Ei，Es分别为入射电场场强和散射电场场强；φ为柱坐标系中方向角度；r为其径向距离。

对k＝4.5的折叠变换式集中器散射放大功能进行了仿真验证与计算。f＝3GHz，k＝4.5时TE平面波从左照射模型的仿真及散射宽度计算结果如图2～4所示。为便于比较，统一σ取值范围为0～5.5m。由图可知：图3（a）集中器中原尺寸模型的散射与图4（a）4.5倍尺寸模型基本相等，且远大于图2（a）原尺寸模型。

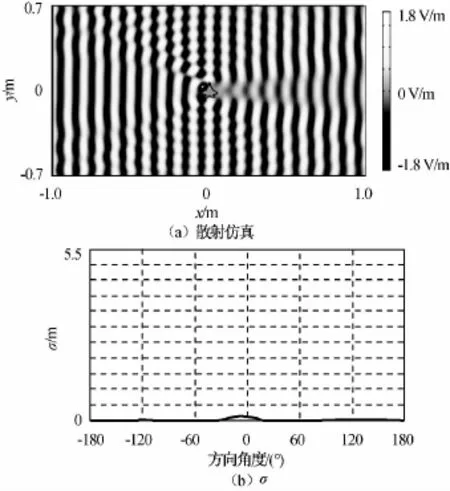
图2 原尺寸隐身飞机仿真和计算结果Fig.2 Simulation and calculation result of stealth aircraft with original size

用类似方法对其他倍率的折叠变换式集中器散射特性也进行了研究，结果验证了图2～4的结论：倍率为k的折叠变换式集中器，对内置物体的散射尺寸，其放大倍数为k（k＞b／a），可实现较高倍率的散射放大。

散射放大作用是一种超散射可用于设计多种新颖的变换电磁学器件［11－12］。在军事领域，折叠变换式集中器可用于诱饵机和干扰机，在防空领域的突防与反突防有潜在的军事价值。

3 参数分析

讨论不同变量（倍率k或器件相对厚度D）下折叠变换媒质参数极值的变化，以及整体参数分布的规律。此处：D＝（b－a）／a。

设a＝0.1m，b＝0.2m，当D＝1时不同倍率k下ε各方向分量极值如图5所示。

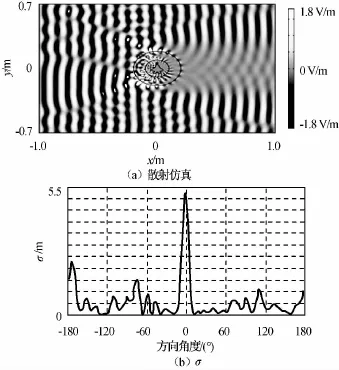
图3 集中器内原尺寸隐身飞机仿真和计算结果Fig.3 Simulation and calculation result of stealth aircraft with original size in concentrator

图4 4.5倍尺寸模型仿真和计算结果Fig.4 Simulation and calculation result of model with 4.5times size

设a＝0.1m，b为0.1～0.4m，s＝0.4m，当k＝4时不同D的ε各向分量极值如图6所示。

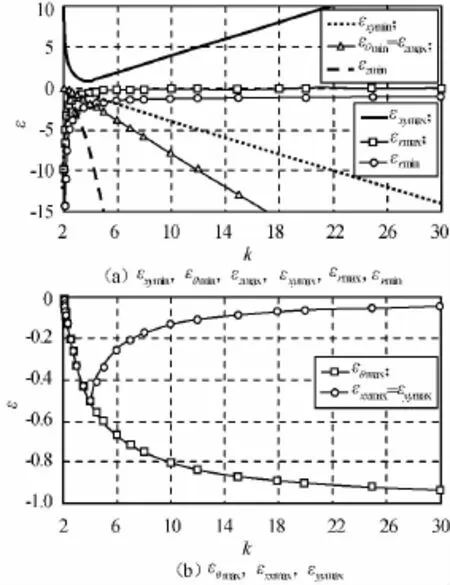
图5 不同k时ε各向分量极值Fig.5 Various component extremums ofεunder different k

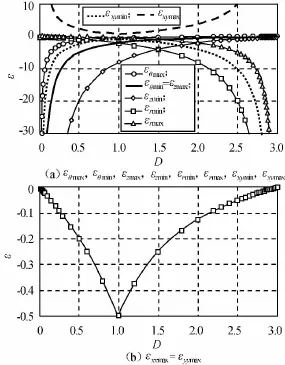
图6 不同D时ε各向分量极值Fig.6 Various component extremums ofεunder different D

归一化参数（η＝（ηmax－ηmin）／ηmax）分别如图7、8所示。由图7可知：ηr，θ，z随k增大而增大，表明随着器件放大能力的提高，变换媒质参数的分布范围不断增大，意味着实际实现的难度加大；ηxx，yy随k先减小后上升，在k＝4处取得最小值75%，综合考虑两者及实现难度，可认为：k＝4是器件设计的最优化倍率值。由图8可知：ηr，θ，z不随D发生变化，保持75%不变；ηxx，yy随D先减小后增大，在D＝1处取得参数分布最小值，综合两者可认为D＝1是器件设计的最优化尺寸。

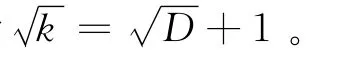
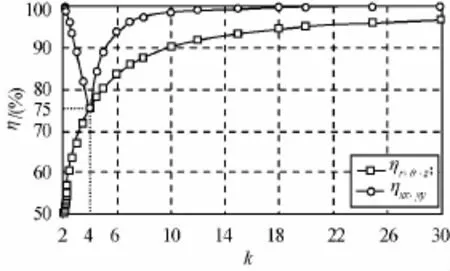
图7 不同k时ηFig.7 Normalized parameter under various k

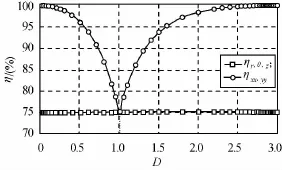
图8 不同D时ηFig.8 Normalized parameter under various D

4 结束语

本文对折叠变换媒质的散射特性和参数进行了研究。仿真计算并验证了折叠变换式集中器变换媒质的散射特性，讨论了折叠变换媒质的参数极值及其归一化分布范围，给出了其最优化设计。研究有一定参考的价值。

［1］ LEONHARDT U.Optical conformal mapping［J］.Science，2006，312：1777－1780.

［2］ PENDRY J B，SCHURIG D，SMITH D R.Controlling electromagnetic fields［J］.Science，2006，312（5781）：1780－1782.

［3］ LI Ting－hua，YANG Jing－jing，HUANG Ming，et al.Arbitrary control of the electromagnetic field in two－dimensional waveguide and slit using metamaterials［J］.Appl Phys A，2011，105：509－515.

［4］ SCHURIG D，MOCK J J，JUSTICE B J，et al.Metamaterial electromagnetic cloak at microwave frequencies［J］.Science，2006，314（5801）：977－980.

［5］ CHEN H，CHAN C T，SHEN P.Transformation optics and metamaterials［J］.Nature Mater，2010，9：387－396.

［6］ ZHANG Kuang，WU Qun，FU Jia－hui，et al.Cylindrical electromagnetic concentrator with only axial constitutive parameter spatially variant［J］.J Opt Soc Am B，2011，28（6）：1573－1577.

［7］ YANG Jing－jing，HUANG Ming，YANG Cheng－fu，et al.Metamaterial electromagnetic concentrators with arbitrary geometries［J］.Opt Express，2009，17（22）：19656－19661.

［8］ LI Wei，GUAN Jian－guo，WANG Wei.Homogeneous－materials－constructed electromagnetic field con－centrators with adjustable concentrating ratio［J］.J Phys D Appl Phys，2011，44：125401，6.

［9］ LI T，HUANG M，YANG J，et al.Three dimensional electromagnetic concentrators with homogeneous material parameters［J］.Progress in Electromagnetics Research M，2011，18：119－130.

［10］ GENTE R，JANSEN C，GEISE R，et al.Scaled bistatic radar cross section measurements of aircraft with a fiber－coupled THz time－domain spectrometer［J］.IEEE Transactions on Terahertz Science and Technology，2012，99：1－8.

［11］ YANG Tao，CHEN Huan－yang，MA Hong－ru，et al.Superscatterer：enhancement of scattering with complementary media［J］.Opt Exp，2008，16（22）：18545－18550.

［12］ LUO Yang，HE Lian－xing，ZHU Shou－zheng，et al.Changing the scattering of sheltered targets［J］.Phys Rev A，2011，83：043809，7.