分离模块化航天器系统评估和优化设计研究

徐 明，王金龙

（1.北京航空航天大学 宇航学院，北京 100191；2.中国民航大学 空中交通管理学院，天津 300300）

0 引言

F6是美国国防高级计划研究局（DARPA）对分离模块概念进行研发验证项目［1］。DARPA对其技术性能和经济优势进行了广泛的研究，投资Lock－heed Martin Company（LM），Northrop Grumman Corporation（NG），Orbital Sciences Corporation（OSC），Boeing Company（BC）等四家公司以价值为中心的设计方法进行F6项目的第一阶段工作，于2009年2月准时完成［2］。第二阶段的工作于2009年11月启动，由OSC公司负责。同时DARPA表示会于2013年实现在轨演示验证。通过F6项目的不断深入研究，研究人员提出了以价值为中心的航天器设计方法（VCDM）［3］。VCDM 通过对寿命期、技术风险、不确定性的多方面考虑，获取最高的投入产出比，达到以最小成本获取最大价值的目标。此方法通过对能力、成本和风险的价值化将设计的技术属性转化到商业范畴，以“净现值”权衡系统优劣［4］。文献［5］研究实现分离模块方式的太空快速响应系统面临的问题，从技术、组织机构支持、经济和政治四个方面进行分析并研究其内在联系。文献［6－7］总结F6项目中取得的成果，对设计方法进行合理化并讨论以价值为中心的设计标准与传统的系统工业过程标准的联系，评价以价值为中心的设计在F6项目中的重要性，重述分离模块航天器的概念，比较分离模块航天器与传统整天航天器的优缺点，并介绍一系列分离模块航天器的设计制造的以价值为基础的技术方法。文献［8］对分离模块航天器和传统航天器进行属性、策略、模型比较，评价分离模块航天器的成本和价值优势。文献［9］比较分析了四家公司设计的VCDM工具模型构架、风险和净现值量化等的工具特征，对参与F6项目第二阶段OSC公司研发的PIVOT工具进行跨学科优化，通过动态生命周期仿真和参数模型评估生命周期成本影响，用非参数的计算机物理模型评估航天器的质量影响，研究结果表明分离模块航天器的生命周期成本较传统整体航天器有优势。文献［10］研究能解决F6项目结构两个难题的设计工具GT－FAST，用实例分析FT－FAST设计工具处理输入、模型、属性、假设的方式。随着分离模块航天器设计的发展，国内许多学者也开始研究相关项目。文献［11］介绍了分离模块航天器的概念和进展，分析和探讨了以价值为中心的航天器设计，对国内的分离模块航天器发展提出启示和建议。文献［12］针对航天器概念设计阶段的不确定多学科设计优化进行研究，验证其可行性和有效性。

本文对分离模块化航天器系统评估和优化设计进行了研究。

1 成本、价值及评估指标

航天器的设计成本包括航天器研制成本和发射运营成本，同时也包含了各种不确定因素存在而可能发生的成本。所有的成本统一量化为货币单位形式进行统计。从航天器设计的准备阶段至其生命周期结束的所有成本的总和构成分离模块航天器的总成本。

VCDM研究的前提是将航天器设计的技术价值定量，每种以价值为中心的航天器设计方法中均有价值化准则对航天器进行价值评估计算，将航天器的实际应用技术转化为定量价值。对价值的定量评估并非绝对测量，而是作为一种评估工具，为任务决策提供信息。在以价值为中心的航天器设计过程中，通过价值量化准则对航天器进行价值量化，考虑不确定性因素对价值生成的影响，直到航天器生命周期结束所获取的价值之和为航天器的总价值。

F6第一阶段项目中，四家公司采用不同商业指标对航天器的成本与价值收益进行评估，不同商业指标的侧重点各异。净现值（NPV）广泛用于经济、金融、会计等领域，是评价设计方案优劣的一种方法。NPV不仅权衡成本与价值收益，而且考虑方案的执行时间问题，反应方案的时间效率。方案决策者通过对NPV的值进行方案决策，决策法则为：净现值为正则采用，净现值为负则不采用，多个备选方案决策时挑选正值最大的方案。为更好地评估航天器系统，本文采用NPV作为评估指标。分离模块航天器系统设计方案优劣以NPV大小衡量，NPV值大表示投入成本少，产出收益大，设计方案优；反之，设计方案劣。引入VCDM 航天器设计中，以NPV值大小权衡航天器的总体投入产出比。NPV可表示为

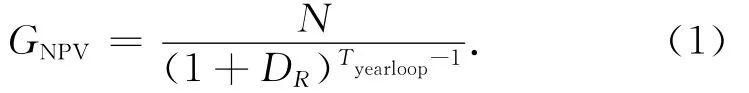
式中：DR为贴现率；N为净现金流；Tyearloop为航天器生命周期。

2 航天器研制模型

2.1 分离模块航天器的体系结构建模

航天器体系结构建模是对航天器成本和价值收益评估的前提。分离模块航天器系统因其结构特征与传统航天器有较大不同，故其体系结构建模也截然不同。国内外分离模块航天器的体系结构建模研究中，较常见的对分离模块航天器层次的定义，从低到高依次为组件、模块、星簇，如图1所示［12］。

组件在航天器中能独立完成某项任务，是分离模块航天器建模中的最小单位。在DARPA的第一阶段任务中，四家公司分别对组件进行建模，主要包括以下。

a）任务的有效载荷。分离模块航天器设计和价值评估最终目标是小成本获得高价值，价值获取的唯一途径是有效载荷。有效载荷通过任务完成获取价值，而不同的任务需要不同的有效载荷完成，如对地观测有效载荷（EO）。

图1 组件、模块和星簇关系Fig.1 Relationship among component，module and cluster

b）测控组件，通过中继卫星实现对星簇的连续测控。

c）任务数据处理组件，星上高性能计算机，用于处理复杂的任务数据。

d）数传通信组件，星上负责星星间、星地间通信和数据下载上传的组件。

e）数据存储组件，如固态硬盘，主要功能为存储有效载荷完成任务而产生的大量数据，为数据传输做准备。在建模阶段通过经验和设备参数对各组件进行属性赋值，如质量、功率、成本、技术成熟度等。

模块由多个组件构成，可在空间中实现独立自由飞行。构成模块的组件除有效载荷等功能性组件外，还包括电源、热控等卫星平台的相关组件。模块的属性取决于其组件和平台的属性，在对组件进行建模并整合后可得到模块的属性。

星簇即分离模块航天器，由多个分离模块编队飞行构成，完成某项或某些目标任务。

航天器系统总体设计包括航天器星体设计和发射运载设计，航天器发射运载方案的建模是航天器系统必不可少的部分。本文发射运载器选择Minotaur I，Athena I，Taurus 2210，Taurus 3110，Minotaur IV，Athena II。发射运载器不同，发射运载能力和可靠性亦不同，发射运载成本会相应有所不同。在发射运载设计方案中，应根据模块设计适当选择。

模块中分离组件的组合、星簇中模块的分割、运载发射设计均会对航天器的成本和价值评估产生影响。航天器的成本与价值的评估对模块中分离组件的组合、星簇中模块的分割和运载发射设计进行优化，使航天器能获得更高的投入产出比。

2.2 航天器系统评估模型

2.2.1 成本模型

分离模块航天器成本主要考虑模块研制成本、发射与运营成本和风险成本三部分。其中：航天器的商业保险成本归入发射与运营成本，暂不考虑地面设备成本与软件开发成本；风险成本考虑由于各种不确定性因素而出现的模块研制时间推迟、发射运载失败、在轨故障等情况维护而需要投入的成本。

成本按属性可分为不可循环和可循环两种，对应有子系统中的可循环使用部件设计和不可循环使用部件设计。这种分类设计主要针对部分方案可重复使用的设备，在第一次计算成本后，第二次的成本核算可在第一次的基础上乘以学习曲线率系数即为第二次使用的成本。分离模块航天器在生命周期内成本计算流程如图2所示。

图2 成本计算过程Fig.2 Procedure to estimate cost during life

a）模块研制成本

航天器总体设计中含有不同的组件模块，不同组件模块的成本各异，同类模块因技术成熟度与研制时间不同也会出现差异。在成本核算中用可循环与不可循环成本分类分别计算。在同一类模块进行研制时，第1个模块包含技术不成熟带来的较高成本，同一类模块的后续研制成本因可循环部件的成本而相对减少。

考虑批量生产，单元模块的成本估算为

式中：Cmodule_i1为第i类模块中第一个模块的研制成本，包括不可循环使用成本Cmodule_i1（NRE）和可循环使用成本Cmodule_i1（REC）两部分；Cmodule_iQ为同类型第Q个模块的成本；LRmodule为该类模块研制生产的学习率。模块给重复成本和重复成本通过模块所携带组件成本进行估算，成本估算公式参考小卫星成本模型（SSCM07）。

令通货膨胀引起的第i类中第Q个模块研制成本溢值为Cmodule_iQ_inflated，有

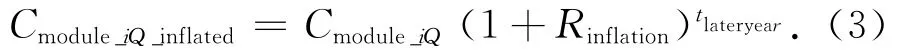
式中：Rinflation为年通胀率；tlateryear为模块研制年时间。所有模块的研制成本

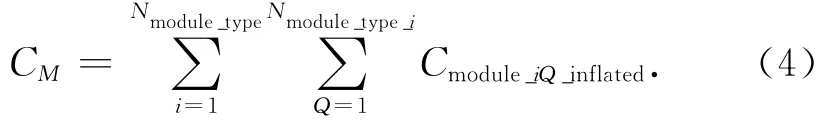
式中：Nmodule_type为分离式航天器包含的所有模块类型数；Nmodule_type_i为第i类模块数。

b）发射与运营成本

发射运载方案根据模块属性进行设计，方案确定后模块的发射运载成本按方案执行成本统计。航天器在总体设计中会对发射运载器产生潜在的约束，有效载荷的安装等限制模块发射的自由组合。不同模块可组合发射，因此发射次数不大于模块个数。

由于发射运载器成本巨大，在技术条件允许时应尽可能减少发射次数，在发射运载器运载能力范围内采取多个模块同一运载器发射。总发射成本为每次发射成本之和。

分离模块航天器在轨运行时，每个模块都可视作独立小卫星，因此在运营成本中按模块进行成本统计。近似定义每个模块每年的运营成本为200万美元，则航天器总运营成本

式中：Tij为第i类型第j模块的在轨运行总时间。

以上两部分之和即为发射与运营成本。若设计方案能理想实现，整个分离模块航天器成本即为模块研制成本和发射与运营成本之和。但实际的空间环境和技术因素等不能保证方案的理想实现，因此整个航天器成本还包括不确定性部分。由不确定性因素而引发的成本不确定项定义为风险成本。

c）风险成本

航天器研制、发射和在轨运行过程中存在各种不确定性因素，导致的任务延期、发射失败、在轨故障等问题均需要成本投入以保证航天器的正常在轨运行。因此，考虑将这些不确定性因素带来的风险转化为以资金度量的风险成本Crisk，以此衡量设计方案的稳健性和可靠性。本文主要考虑发射失败和在轨故障两种情况。

一是发射失败。若发射失败，则该次发射所携带的模块需重新研制和发射。假设重新发射的模块和运载器不变，发射失败的风险成本

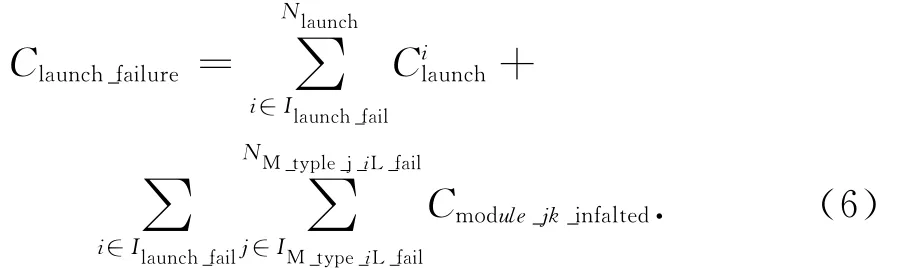
式中：为第i个运载器的发射成本；Ilaunch_fail为发射失败运载器对应的发射编号；IM_type_iL_fail，NM_type_j－iL_fail分别为发射失败运载器i携带的模块类型编号及其数量；Cmodule_jk_inflated为第j类中第k个模块研制成本溢值。

二是在轨故障维修。若分离模块航天器在轨出现故障，采用发射同型模块对故障模块进行在轨更换实现故障维修，则在轨故障维修成本为该新模块的研制成本与发射成本之和，即

式中：Claunch_ops_failure，Nops_failure分别为在轨运行故障模块更换所需发射成本和次数；IM_type_iops_failure，NM_type_j－iops_failure分别为在轨故障模块类型编号及其对应故障模块数量。

则有

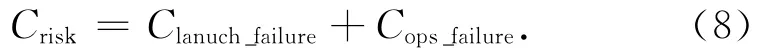
综上所述，分离模块航天器总成本为模块研制成本、发射与运营成本和风险成本的总和。

2.2.2 价值模型

收益模型是衡量航天器价值收益的标准。分离模块航天器因模块多，携带载荷的功能和工作方式不同，所属的通信方式也各异。价值模型应将载荷产生的价值趋于一个可衡量的统一量，最终换算成货币量的形式。

航天器的任务都需要根据通信链路传输到地面，所有载荷工作产生的价值均以数据形式表示。在航天器的价值模型中，对数据采取不同的加权因子而进行价值货币化。不同载荷对数据的敏感程度和获取量不同，同时数据的重要性也不同。目标任务重要的数据加权时应取较大的加权因子，反之，则应使用较小的加权因子。

通信链路的有效性对价值模型也有影响。航天器设计中常存在多种通信链路，每种链路的通信的速率和有效率不同，相同的载荷通过不同的链路传输，得到的价值不同。对数据传输的计算主要是基于航天器根据轨道定义计算出的过顶的次数和时间，通过对高速率和低速率空地传播的有效过顶次数的统计，确定过顶的具体时间值。同时，对各种数传链路的可靠性进行计算从而得到可信数据量，以可信数据量进行价值计算。

若两个载荷分别采用LR_SG，HR_SG，LR_247三种方式进行数传，计算价值

式中：δi，δj分别为载荷i，j的加权因子；Ni_LR_SG，Nj_LR_SG，Ni_HR_SG，Nj_HR_SG，Ni_LR_247，Nj_LR_247分别为载荷i，j通过LR_SG，HR_SG，LR_247数传方式得到的有效数据量。分离模块航天器生命周期内价值收益计算流程如图3所示。

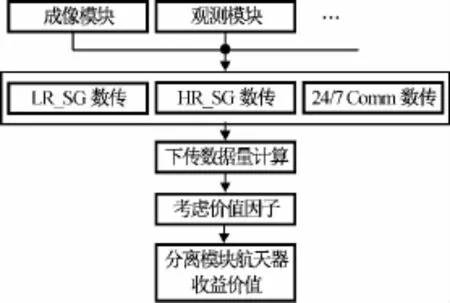
图3 航天器价值计算流程Fig.3 Estimation procedure of value during life

2.2.3 不确定性模型

以价值为中心的航天器设计方法中，除受模型精确度的影响外，影响成本与价值评估的准确度主要是确定性因素。不确定性模型建立的准确度和全面性对成本与价值评估的准确度产生重大影响。在航天器的生命周期内，不确定性因素时时对航天器产生影响。主要影响可分为对成本模型的影响和发射运营的影响。

成本模型的不确定因素分布在模块成本、发射成本和操控成本中，根据经验和技术成熟度TRL设定不确定性因子的上界和下界。同时利用与成本和价值水平相关的参数进行不确定性成本的计算，如离散率、学习曲线率、发射运载学习曲线率、保险成本因子、通货膨胀率、年平均操作成本等。

三角形分布是工程项目成本风险理论中最广泛应用的模型。通过三角形分布可从中预测最大、最小和最可能的值，靠近最大、最小值的值出现的可能性小于靠近最可能值的值。各种不确定性的概率分布不同，但通过三角形分布可较准确地对各种不确定性进行研究。本文用三角形分布对不确定性进行建模，以成本不确定性为例进行研究。设成本上限和下限分别为Cmax，Cmin，标准期望成本为Cs，判定因子A＝（Cs－Cmin）／（Cmax－Cmin）。用随机变量p进行随机判定：若p≤A，则

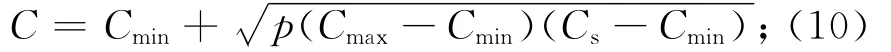
若p＞A，则

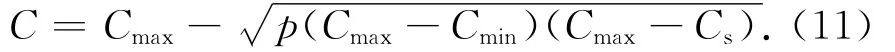
不确定模型对发射运营阶段的航天器的影响主要体现在发射是否成功、模块是否出现在轨故障等，这些均会对成本与价值产生影响。发射成功与失败的不确定性模型依赖于发射运载器的可靠性，而模块在轨故障的不确定性模型依赖于模块的可靠性。

以上不确定性模型均将不确定性因素作为随机变量，利用概率论中的事件概率处理方法对相应的成本与价值进行核算。

3 成本与价值评估流程

实现分离模块航天器的成本与价值评估需按航天器生命周期的时间历程。航天器的生命周期大致分为模块设计与研制、发射运载、在轨调试与运营三个阶段，每个阶段内分别对成本与价值进行核算，最终在航天器生命周期截止时得到总体的成本与价值。评估流程如图4所示。

在设计的初始化阶段主要是对相关参数的定义赋值，由用户选择航天器任务设计过程中需考虑的不确定性因素，用户自行选择功能组件进行组装成模块及模块的发射运载。相关参数的赋值包括对分离模块航天器飞行环境参数定义和模块物理参数、卫星平台、数传特性等参数的设置。模块研制和发射日程表的变化、发射失败、在轨失败等不确定性因素由用户自行设置。在对地观测载荷、高带宽通信组件等功能性组件满足组件组合约束的条件下，用户根据任务内容设计。

设计阶段的成本按需求对不确定性因素选取、通货膨胀率等进行计算汇总。按航天器在此阶段所耗费的成本进行累加。若考虑模块研制时间延迟等不确定性因素，则应根据通货膨胀率、延迟时间等计算风险成本。由于此阶段的航天器并未在轨，不能创造价值，不考虑价值。

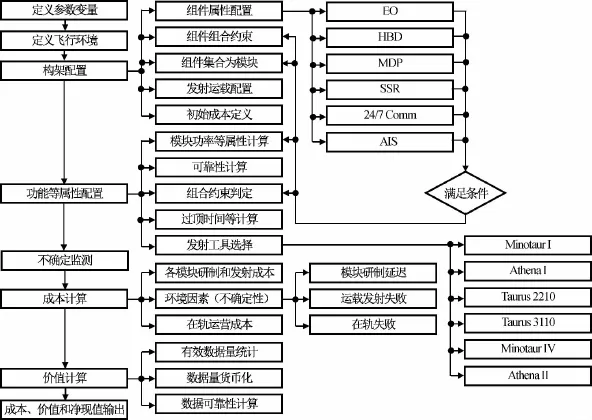
图4 分离模块航天器成本与价值评估流程Fig.4 Estimation procedure of value and cost during life

航天器的不同模块按用户设计方案依次进行发射。若发射方案中不考虑不确定性因素，则仅计算发射运载成本。如用户选择考虑发射失败、发射延迟等不确定性因素，成本计算应包括风险成本。由于发射运载成本巨大，用户在设计模块组合发射时应考虑发射运载器的可靠性和模块的研制成本，将发射失败后所耗费的风险成本降至最低。发射阶段由于模块还未进行正常运作，未产生价值收益，故收益为零。

在轨调试部分的持续时间为1个月，可与在轨操控阶段联合计算。从在轨操控部分开始，模块的功能组件能开始在轨运作，能产生价值收益。不同功能组件产生的不同技术收益均通过数传方式获取。数据量大小可衡量收益多少。但不同功能组件的技术收益的实际利用价值不同，在计算价值收益的过程中除考虑数传方式不确定性外，还要加入价值因子，将不同功能组件的收益根据利用价值的效率价值化。

成本与价值收益在此阶段均受不确定性因素的影响。模块在轨运行受到不确定因素影响、模块寿命到期等可能会使模块功能失效，若用户选择模块替换，则将替换模块的研制成本和替换模块的发射运载成本作为风险成本加到航天器的总成本中。在此替换期间，失效模块不产生价值，价值收益应停止计算。

分离模块航天器的成本和价值收益按此流程计算，直至航天器生命周期终止。根据得到的成本与价值收益，考虑生命周期的时间项得出评估指标NPV的值。

4 基于遗传算法确定性多学科优化

价值导向的评估方法可自定义输出多种目标结果，包括平均成本的期望值和方差、平均收益的期望值和方差、净现值等，导致优化过程本质是求解Pareto意义下多目标最优问题。在具体操作过程中，需针对不同目标结果的权重系数，比较优化结果连续性（剔除突变的设计结果）。

用通用优化平台的确定性多学科优化问题，无法甄别对优化过程影响微弱的参数，将蒙特卡罗仿真转化为优化迭代，导致搜索效率下降。迭代过程的本质是各种情况的并行比较，本文考虑搜索效率和平台实用性，用遗传算法作为计算平台对分离模块航天器进行参数优化。

VCDM工具的最终目的就是在精确建立的航天器平台及各模块的模型、不确定性模型，通过遗传算法的初始化、个体评价、选择运算、交叉运算、变异运算直至满足终止条件，最终获得好的成本与价值关系。分离模块航天器的评估并非绝对评估计算，而是相对比较并为分离模块航天器设计方案提供参数优化根据。通过航天器系统成本与价值的评估，确定主要影响因素，通过调整参数达到航天器系统的最优投入产出比。

在分离模块航天器系统优化过程中，先对航天器系统进行建模，包括体系结构建模、发射运载方案设计、成本价值和不确定性建模。其次，确定优化目标和优化参数。优化目标根据航天器任务要求而具体确定，若要求航天器经济稳定性好，则应将任务的优化目标设置为NPV方差最小；若要求航天器投入产出比最高，则将任务的优化目标设置为NPV均值最大。之后，用遗传算法寻找最优方案。分离模块航天器优化设计流程如图5所示。

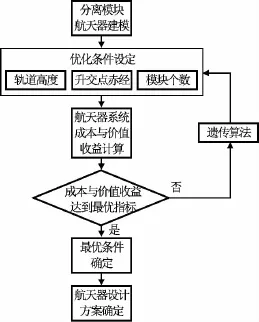
图5 优化设计方法流程Fig.5 Optimization procedure of NPV during life

5 实例仿真

分离模块航天器的系统评估和优化设计均按航天器的生命周期历程进行，通过对整个生命周期内航天器的模块研制、发射与运营等阶段的成本与价值核算得到系统评估值，用户根据任务确定优化目标，通过遗传算法平台得到分离模块航天器的优化参数。

5.1 系统评估

取航天器轨道高度500km，降交点地方时为上午10：30，轨道为太阳同步轨道。航天器设计研究任务在1月份开始，模块的设计时间为2年，生命周期为5，10年。可分离组件6个，其相关参数见表1。表中：FIT为1 000h内失败次数，是表征组件可靠性的参数。

表1 可分离部件性能和参数设置Tab.1 Parameters of separable components

考虑成本不确定性、日程表变化、发射失败、在轨故障失败、商业保险、模块替换等因素，得NPV见表2、3。两种生命周期的航天器的成本与价值计算结果见表4、5。

分别将置信水平设置为0.5，0.68，用蒙特卡罗方法所得两种生命周期的航天器的成本和收益分别如图6、7所示。

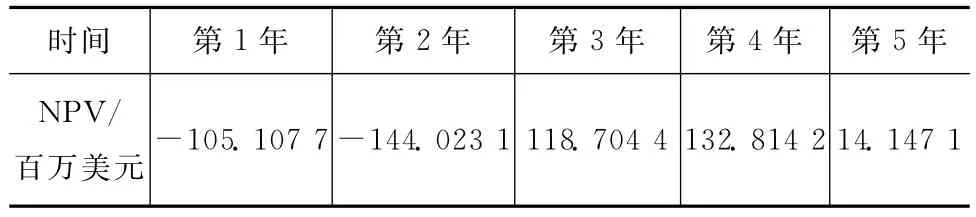
表2 5年生命周期航天器的净现值NPVTab.2 History of NPV during 5years

表3 10年生命周期航天器的净现值NPVTab.3 History of NPV during 10years

生命周期不同，成本和价值就会不同。生命周期长，在轨操控成本、模块替换成本等会相应增加，同时创造的价值也会增加。因此，航天器生命周期10年的成本和价值与5年的相比较会有较大的增大。

表4 5年生命周期航天器的平均成本与收益Tab.4 Cost and value of fractionated spacecraft during 5years

表5 10年生命周期航天器的平均成本与收益Tab.5 Cost and value of fractionated spacecraft during 10years

图6 航天器成本与价值分布（5年）Fig.6 Ergodic representation of value and cost for fractionated spacecraft during 5years

图7 航天器成本与价值分布（10年）Fig.7 Ergodic representation of value and cost for fractionated spacecraft during 10years

NPV值是多种不确定性因素共同作用的结果，与分离模块航天器的生命周期长短无关系。远离置信区间的点是多种不确定因素同时发生的结果，在实际工程实践中可能性极小，评估中不予考虑。

分离模块航天器不同模块数的NPV值如图8所示。整体航天器在初期阶段的投入产出比优势较显著，随着时间延长，分离模块航天器的投入产出比越来越高。这与F6项目中对分离模块航天器的技术论证相符。

图8 不同模块数航天器净现值NPV分布Fig.8 NPV of spacecraft with various number of fractionated modules

5.2 航天器系统优化设计

对生命周期5年的分离模块航天器进行优化，优化变量为轨道高度、降交点地方时和模块数，各自的约束边界分别为［400，700］km，［9，13］h，［1，6］。遗传算法参数为：进化代数50，每代种群数100。以最大化NPV均值为目标，所得优化结果如图9所示：轨道高度573.715km，降交点地方时11.237，模块6个。以最小化NPV的标准差作为目标，所得优化结果如图10所示：轨道高度598.939 6km，降交点地方时11.32，模块数1个。

图9 以NPV均值为目标的优化结果Fig.9 Optimal scheme refined by mean of NPVs

系统优化设计初始化的寻优条件中设置的模块数为1～6，寻优过程中遗传算法根据优化目标要求对模块数及轨道高度和降交点地方时进行寻优以获取更好的优化目标。以NPV均值最大为优化目标所得结果表明：分离模块航天器的投入产出比高于整体航天器，在此模型专中模块个数为6时，航天器获取最高的净现值。系统优化设计的优化目标不同，所得优化结果也不同。若保持航天器模型和寻优条件不变，以NPV的标准差最小为优化目标，则模块为1的航天器最优，即整天航天器的稳定性更高，与实际工程实践相符。

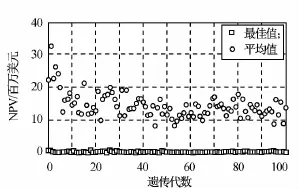
图10 以NPV方差为目标的优化结果Fig.10 Optimal scheme refined by variance of NPVs

在建立航天器模型基础上，用户可根据具体航天器任务设定不同的优化目标，用遗传算法的优化计算，得到优化目标最优时的优化条件参数。航天器系统的评估目的是对已设计的航天器系统进行成本与价值收益评测，而确定性学科的优化设计则根据用户的需求为目标，对航天器系统参数进行调整寻优，保证用户得到更高的投入产出比。

6 结束语

本文用VCDM方法对分离模块航天器进行设计，建立成本模型、价值模型和不确定性模型。对模块功能组件按模块的物理约束、功能约束和用户需求进行组合设计，在发射运载器承载能力范围内，设计航天器的模块组合发射方案。对分离模块航天器生命周期内的模块研制、发射运载、在轨操控三个阶段的不确定性进行分析，根据三角形概率分布计算航天器的风险成本。统计整个生命周期的成本与价值收益，得到分离模块航天器的总成本和总价值收益。用蒙特卡罗方法得到不同不确定性因素影响下的航天器总成本和总价值收益并进行分析。基于遗传算法以NPV为优化目标对分离模块航天器设计进行确定性学科优化，得到的优化条件可作为航天器设计参数，能达到NPV最大。

分离模块航天器以其技术性能和经济优势受到越来越多重视，以价值为中心的航天器设计方法VCDM能评估航天器的投入产出比，在航天器设计中具有极大的指导意义。对成本与价值评估的确定性学科优化能直接为设计者提供最优的参数值，在未来的航天器设计中将会起到重要的作用。

［1］ BROWN O C，EREMENKO P.Value－centric design methodologies for fractionated spacecraft：Progress summary fromphase1of the DARPA system F6program［R］.AIAA，2009－6540.

［2］ McCORMICK D，BARRETT B，CLAPP－BURNSIDE M.Analyzing fractionated spacecraft architectures using RAFTIMATE－A Boeing tool for valuecentric design［R］.AIAA，2009－6767.

［3］ EICHENBERG B E，WISNIEWSKI M J，CHOI S W，et al.Using a value－centric tool framework to optimize lifecycle cost，value，and risk of spacecraft architecture［R］.AIAA，2009－6765.

［4］ O’NEIL D A，MANKINS J C.The advanced technology lifecycle analysis system （ATLAS）［R］.IAC－04－IAA.3.6.3.01.2004.

［5］ RICHARDS M G，ZOE S，O’NEILL M G，et al.Implementation challenges for respnsive space architectures［R］.AIAA，RS7－2009－2004.

［6］ BROWN O.The value proposition for fractionated space architectures［R］.AIAA，2006－7506.

［7］ BROWN O.Application of value－centric design to space architectures：the case of fractionated spacecraft［R］.AIAA，2008－7869.

［8］ MATHIEU C，WEIGEL A L.Assessing the flexibility provided by fractionated spacecraft［R］.AIAA，2005－6700.

［9］ O’NEILL M G，YUE H，NAG S，et al.Comparing and optimizing the DARPA system F6program valuecentric design methodologies［R］.AIAA，2010－8828.

［10］ LAFLEUR J M，SALEH J H.GT－FAST：apoint design tool for rapid fractionated spacecraft sizing and synthesis［R］.AIAA，2009－6802.

［11］ 刘 豪，粱 巍.美国国防高级研究计划局F6项目发展研究［J］.航天器工程，2010，19（2）：92－98.

［12］ YAO Wen，CHEN Xiao－qian，ZHAO Yong，et al.A fractionated spacecraft system assessment tool based on lifecycle simulation under uncertainty［J］.Chinese Journal of Aeronautics，2012，25：71－82.