确定贮箱流固耦合纵向振子模型参数的有限元方法

韦 笑，杨琼梁，张美艳，唐国安

（1.复旦大学 力学与工程科学系，上海 200433；2.上海宇航系统工程研究所，上海 201109）

0 引言

液体运载火箭的结构振动与推力脉动存在耦合，这种耦合可能使运载火箭在主动飞行段产生较大的动态响应，甚至使其发生纵向不稳定振动。因此，对运载火箭进行动力稳定性的分析对火箭飞行安全有重要意义。分析稳定性时，需建立贮箱及推进剂的纵向振动模型，其中弹簧振子模型因其简便、高效而在工程中被广为采用［1］。1961年，文献［2］提出了贮箱液固耦合的纵向质量－弹簧模型。文献［3］对Wood模型中的贮箱箱底模型进行了进一步研究，修正了贮箱和推进剂弹簧振子模型中的3个刚度系数。文献［4］将贮箱筒壁及箱底置于同一分析模型，用实验进行了对比分析。文献［5］用经典板壳理论中的无矩板理论得到贮箱筒壁的动力学方程，对Wood模型中贮箱筒段模型部分进行了细化与改进。文献［6］提出了一种贮箱流体多自由度的质量－弹簧模型。贮箱和推进剂的弹簧振子建模方法及刚度系数计算公式至今仍被应用，但为能用壳体理论推导出刚度系数的计算公式，必须对贮箱的变形和受力引入多种假设，如筒段和箱底被认为是等厚度的各向同性均质薄壳，且壳体内只有面内的张力和剪力，而无弯矩和扭矩。对实际工程中通过加筋等工艺提高强度和刚度的薄壳容器，必须经壁厚等效等处理后才能套用经典的壳体理论。此外，新型复合材料壳体具明显的各向异性，这也将增大经典壳体理论分析的难度。

有限元方法是一种通用的方法，不受各向异性、非均质／变厚度壳体等限制。用有限元方法计算贮箱在液体压力及上面级箭体载荷作用下的箱体变形和液体质心位置变化可获得较高精度。有限元与纵向振动弹簧振子的建模方法结合，能克服经典壳体理论的局限，适应更复杂箱体结构的贮箱和推进剂建模。本文用有限元方法对贮箱流固耦合纵向振子模型参数的确定进行了研究。

1 贮箱和推进剂纵向振动的弹簧振子模型

液体火箭推进剂贮箱常为圆柱形箱体，且其结构部分一般由前底、筒段、后底三部分组成。箱底的底形可分为半球形底、半椭球形底、锥形底和三心底等，筒段则多为圆柱壳。半椭球底柱形贮箱如图1（a）所示。在纵向振动简化分析时，箱内液体以及与液体接触部分的壳体（贮液段）可等效为由弹簧和质量组成的振子模型，如图1（b）所示。通常，振子模型包含1个质量参数Mp和3个刚度参数k1，k2，k3，其中Mp为贮箱内液体质量。

图1 贮箱箱体与贮液纵向耦合振动的振子模型Fig.1 Structure and deformation of tank

为确定振子k1，k2，k3，考虑以匀加速度上升的贮箱段箱体，在液体压力p（x）和上面级箭体载荷F的作用下，贮液段箱体将发生变形，设筒段上下两端的位移分别为x1，x0，并约定位移方向向上为正。箱内液体的质心也将发生改变，位移量为xp。用振子等效该段箱体和箱内液体纵向耦合振动模型的原则为：当图1（b）所示的振子上端受F、质量块受惯性力作用时，振子的上下端点及质量块分别出现与x1，x0，xp相同的位移量。据此原则，确定振子刚度参数的关键是计算在F，p（x）作用下贮液段箱体的变形。

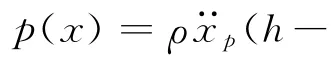
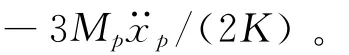
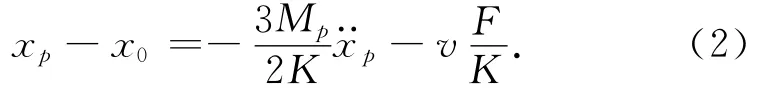
用式（1）、（2）消去变量F，并由关系x1－x0＝（x1－xp）＋（xp－x0）可得液体质心位移控制方程

对图1（b）的弹簧－质量振子，易得液体质心位移控制方程为

由式（3）、（4），可确定振子模型中的二个参数

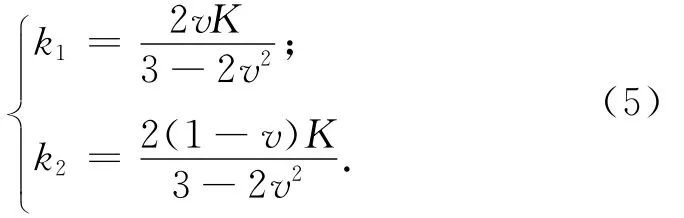
振子模型中3个弹簧串－并联后的刚度就是贮箱贮液段的纵向刚度K，则第三个刚度参数

在微小动态扰动前提下，无论结构是否均质或各向异性，位移都可用柔度系数表示为外载荷的线性函数

2.4 影响新生儿黄疸严重程度相关危险因素的Logistic回归分析 以新生儿黄疸病情轻重程度作为因变量，将胎龄、胎儿出生时体质量、头颅血肿、喂养方式、开奶时间、母婴血型不合6因素作为回归性分析的自变量，建立Logistic回归模型。结果显示:开奶时间、母婴血型不合、喂养方式是新生儿黄疸病情严重程度的主要危险因素(P<0.05)。见表3。

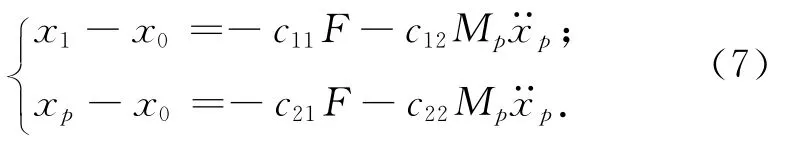
根据位移互等定理和柔度矩阵的正定性，有c21＝c12＞0且c11c22＞c12c21［7］。从式（7）中消去变量F，可得

比较式（4）、（8），可确定振子模型中的第一、二个弹簧的刚度系数

与式（6）类似，第三个弹簧的刚度系数

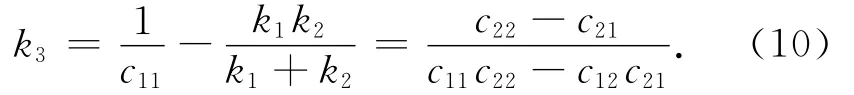
对柔度系数，可用通用程序用有限元方法计算。设计两组计算工况：

则，可得式（7）中的柔度系数为

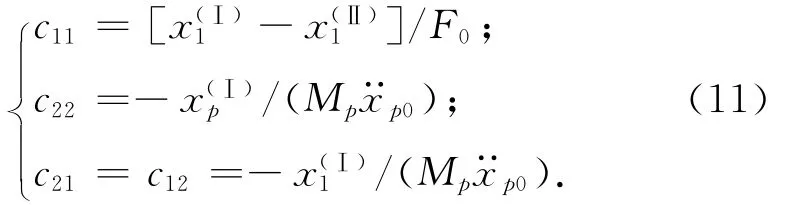
2 液体质心在贮箱变形后位置计算

建立贮箱贮液部分的有限元模型如图2（a）所示。此处仅示意了无加强筋的箱体结构，但由有限元方法的特点可知，对更复杂的箱体结构变形也能进行建模计算。有限元计算能给出模型中每个节点的位移分量，且可认为模型中每个单元在变形后的位置是确定的。

定义液体的质心坐标为

其中积分区域为变形后液体所占据部分的三维空间。

图2 贮箱有限元模型Fig.2 Finite element mesh of propellant tank

根据高斯公式，有

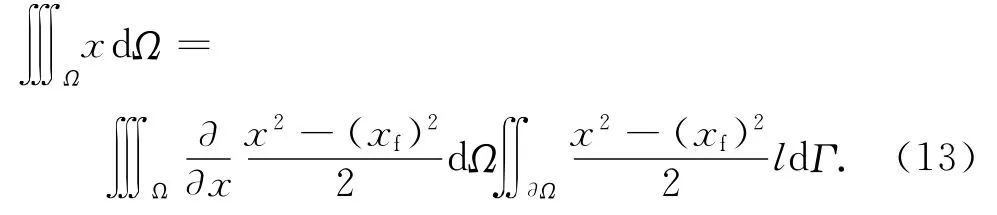
式中：∂Ω为贮箱内液体的整个表面，包括自由面以及与箱壁的接触面；Γ为对应的表面积；l为液体表面外法线方向余弦［lmn］的x轴分量；xf为变形后液体自由面高度［8］。

在自由面上x＝xf，故只须在液体与箱体接触面上积分，且该积分可通过对每个四边形壳体单元进行数值积分后求和而得，即

定义式（12）中的分母也可用相同方式计算积分

变形后液体的自由面高度xf与箱体变形有关，须根据液体的不可压缩性确定。将积分式（15）理解为平面x＝xf与箱体曲面围成的三维单连通区域的体积，该体积为变量xf的函数。因贮箱内推进剂体积恒为Mp／ρp，故可求解非线性方程

确定自由面位置。此处：ρp为贮箱内推进剂的密度。式（16）可用二分法求得其数值解［9］。

箱体变形、液面下降后，液体自由面通常不再与箱体有限元模型的单元边界重合，如图2（b）所示。为此，可用计算机图形学中的多边形裁剪算法，先对自由面附近的箱体单元进行裁剪，再对式（14）、（15）进行积分［10］。

3 运载火箭纵向振动的贮箱建模应用

为验证本文方法，以椭球底柱形贮箱为例进行数值计算。该贮箱贮液部分表面分布节点6 041个，共被划分为6 000个有限元网格。取贮箱数据为：筒段内贮液高度h＝8m；筒段半径R＝1.675m；后底短轴r＝1.047m；短长轴之比n＝0.625；贮箱筒段厚度t＝4.59mm；后底厚度tBH＝2.00mm；E＝6.8×1010Pa；v＝0.33；贮箱材料密度ρ＝2.8×103kg／m3；贮液密度ρ0＝1.0×103kg／m3。算例中贮箱内加注的液体为水。计算柔度时，取Mp＝76 575.6kg，x··p＝9.8m／s2；F0＝750 441N。有限元计算程序选用MSC.Nastran。用本文有限元计算方法计算各项数值结果为：c11＝2.435 6×10－9N／m，c21＝7.346 9×10－10N／m，c22＝4.759 6×10－9N／m。代入式（9）、（10）所得振子模型的3个纵向等效刚度系数见表1，与用文献［2］无矩壳方法所得相应的刚度系数比较，两种方法的差异见表1。

表1 两种方法算得刚度系数Tab.1 Stiffness of two kinds methods

4 结束语

本文提出了一种用有限元标定确定液体火箭推进剂贮箱振动简化模型纵向刚度的方法。通过模拟解析解法建立等效力学模型的过程，设定仅贮液和贮液且施压两种工况，根据贮箱形变和液体质心位置变化性质，推导出刚度系数的计算公式，数值计算结果与传统无矩壳方法基本符合。该方法不仅适于外形规则的贮箱，也能用于难以计算解析解的异形贮箱及贮箱表面加固有筋条等工况，方法的通用性较传统几何计算方法等有明显提高。该方法的分析计算结果可为充液航天器的燃料贮箱结构设计提供理论依据。

［1］ 周思达，刘 莉.运载火箭贮箱流固耦合分析方法综述［J］.强度与环境，2010，37（3）：52－63.

［2］ WOOD J D.Survey on missile structural dynamics［R］.TRW Space Technology Labs，STL－7102－0041－NU－000，1961.

［3］ PINSON L D.Longitudinal spring constants for liquid－propellant tanks with ellipsoidal ends［M］.Washington DC：National Aeronautics and Space Administration，1964.

［4］ GORMLEY J F，KANA D.Longitudinal vibration of a model space vehicle propellant tank［J］.Journal of Spacecraft and Rockets，1967，4（12）：1585－1591.

［5］ EULITZ W R，GLASER R F，KANA D，et al.Longitudinal vibration of spring－supported cylindrical membrane shells containing liquid［J］.Journal of Spacecraft and Rockets，1968，5（2）：189－196.

［6］ 王其政.结构耦合动力学［M］.北京：中国宇航出版社，1999.

［7］ 付宝连.关于功的互等定理与叠加原理的等价性［J］.应用数学和力学，1985，6（9）：813－818.

［8］ 李菊娥.应用高斯公式应注意的一个问题［J］.高等数学研究，2000（1）：4.

［9］ 王海涛，朱 洪.改进的二分法查找［J］.计算机工程，2006，32（10）：60－62.

［10］ 王志强，王世萍.多边形裁剪算法［J］.西部电子，1994，5（4）：47－52.