巧用一次函数图像解决实际问题
□江苏省苏州市平江中学校 翁余
巧用一次函数图像解决实际问题
□江苏省苏州市平江中学校 翁余
数与形是数学学习与研究永恒的话题,它们就像是一个硬币的两个面。形是数的载体,数是形的内涵。因此,对于数与形的研究,我们不能割裂地来看待,必须使其有机结合,使问题迎刃而解。
数形结合 函数图像 变式问题
在初中数学教学中,我们常常强调“数形结合”,通常指的是“以数助形”或是“以形解数”,即利用数与形的有机结合,使得原本抽象、复杂的问题变得简单、具体。下面,结合自己的教学实践与体会,笔者以运用一次函数图像解决实际问题为例一探数形结合之妙用。
一、利用函数图像解决实际问题的价值所在
把实际场景转化为函数图像的过程,实质上就是建立了知识间的关联,形成了知识的迁移,因而对发展和优化学生的认知结构十分有益。同时,在学生分析与解决问题的过程中,画函数图象是十分重要的步骤,它可以促进学生能更好地思维,使他们学会有序推理和抽象思维。与此同时,画图思考的过程还促进了数学与其他学科的联系。
二、利用一次函数图像解决实际问题的应用分析
【例1】(1)自凌晨0点起至中午12点整,时针和分针重合几次?
(2)它们第二次相遇是在什么时间?
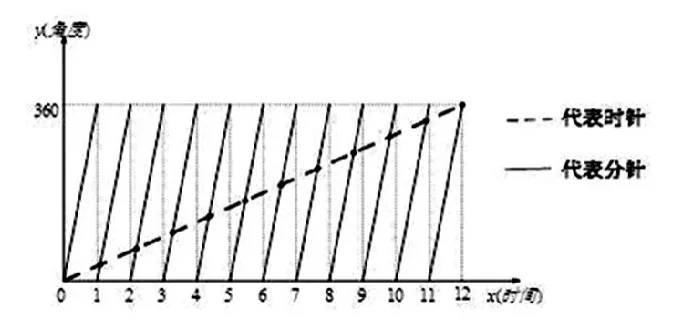
【分析】(1)建立如图所示直角坐标系,横轴代表时间,纵轴代表时针(分针)转过的角度。由于时针每12小时转一圈即转360°,所以代表时针的一次函数图像一定经过(0,0)和(12,360),从而得到代表时针的一次函数图像。分针1小时转一圈即转360°,所以1点整的时候代表分针的一次函数图像经过(1,360),2点整的时候代表分针的一次函数图像经过(2,360)……以此类推,同样可以得到代表分针的一次函数图像。在同一直角坐标系中分针与时针图像共有11个交点,即代表它们相遇了11次。(2)由图像知分针与时针第二次相遇在2点至3点之间,此时,y时针=30x,y分针=360x-720,交点坐标为),所以第二次相遇的时间为2点分。
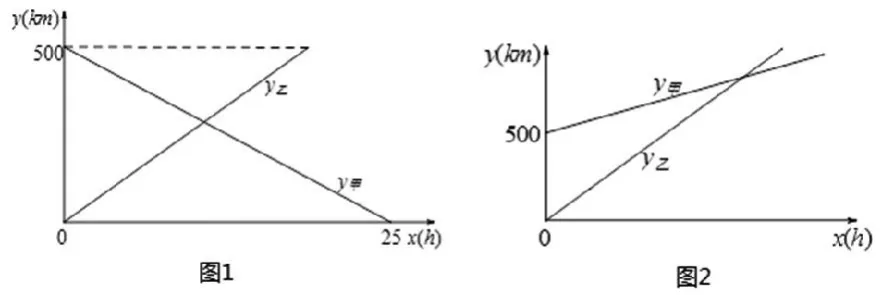
【例2】若A、B两站间的路程为500km,甲速20km/h,乙速为30km/h,甲乙两车分别从A、B两地同时出发。
(1)若两车相向而行,几小时后两车相遇?
(2)若两车相向而行,问经过多少小时他们相距100km?
(3)若两车同向而行,问经过多少小时他们相距100km?

【分析】在函数关系式y=kx+b中,|k|即车速,b为函数与纵轴交点的纵坐标。(1)建立如图1所示平面直角坐标系,则y甲=-20x+500,y乙=30x,交点(10,300),所以两车相向而行,10小时后两车相遇。(2)两车相距100km,应该包含两种情况:①两车相遇前相距100km;②两车相遇后相距100km,用数学表达式可以归纳为:|y甲-y乙|=100。把(1)中的两个函数关系式代入求解即可。(3)与第(2)小题的区别是运动方向由“相向而行”改为“同向而行”,根据题意原来甲乙之间距离为500km,同向而行后相距100km,那么只可能速度快的乙在后,而速度慢的甲在前,因此建立如图2所示平面直角坐标系,得到:y甲=20x+500,y乙=30x,代入|y甲-y乙|=100,从而得到答案:两车同向而行,经过40小时或60小时他们相距100km。
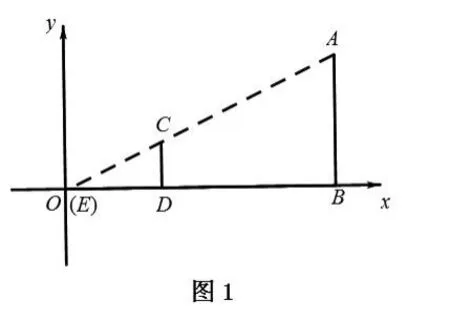
【例3】路边有一路灯杆AB,小明手中拿着一把长为1米的米尺,在灯光下,在点D处测得竖立的米尺影长DE=2m。
(1)若此时测得米尺离路灯底部的距离BD=10m,求路灯杆AB的高度。
(2)若小明沿DB方向继续前行5米到达点G处,此时测得竖立的米尺影长HG=1m,求路灯杆AB的高度。
【分析】以E为坐标原点建立如图所示直角坐标系,(1)很明显E(0,0)、C(2,1),所以直线CE:y=x,而点A横坐标为12,代入解析式可以求出纵坐标为6,即灯杆AB的高度为6米。(2)由F(7,1)、H(6,0)得直线FH:y=x-6,它与直线CE交点A的坐标为(12,6),因此灯杆AB的高度为6米。
三、利用图像解决实际问题的教学思考
在初中阶段培养学生利用“数形结合”的方法观察、分析问题,对发展数学思维也有非常大的帮助,学生将终生受益。

