旋转复合材料薄壁轴的不平衡非线性弯曲振动
第一作者任勇生男,博士,教授,1956年7月生
旋转复合材料薄壁轴的不平衡非线性弯曲振动
任勇生,张兴琦,代其义
(山东科技大学机械电子工程学院, 青岛266590)
摘要:研究几何非线性复合材料薄壁轴在偏心激励作用下的非线性振动特性。在轴的应变位移关系中引入Von Kármán几何非线性,基于Hamilton原理和变分渐进法(VAM)导出复合材料传动轴的拉-弯-扭耦合非线性振动偏微分方程组。为了着重研究轴的横向弯曲非线性振动特性,在上述模型中忽略轴向变形和扭转变形,得到轴的横向弯曲非线性振动偏微分方程,其中考虑了黏滞外阻和内阻的影响。采用Galerkin法,将偏微分方程转离散化为常微分方程,在此基础上利用四阶Runge-Kutta法对常微分方程组进行数值模拟,获得位移时间响应图、相平面图和功率谱图,研究了外阻、内组、偏心距和转速对非线性振动响应的影响,发现旋转复合材料薄壁轴存在混沌运动。
关键词:非线性振动;复合材料薄壁轴;旋转轴
基金项目:国家自然科学基金(11272190);山东省自然科学基金(ZR2011EEM031);山东科技大学研究生科技创新基金项目(YC130210)资助项目
收稿日期:2014-06-18修改稿收到日期:2014-07-30
中图分类号:TH113文献标志码:A
Nonlinear bending vibration of an unbalanced rotating composite thin-walled shaft
RENYong-sheng,ZHANGXing-qi,DAIQi-yi(College of Mechanical and Electronic Engineering, Shandong University of Science and Technology, Qingdao 266590, China)
Abstract:The dynamic behavior of rotating composite thin-walled shafts with geometrical non-linearity was studied here. The nonlinear tensional-bending-torsional vibration equations for a rotating composite thin-walled shaft were derived using Hamilton’s energy principle and variational-asymptotical method (VAM). On the basis of von Karman’s assumption, the geometrical nonlinearity was included in the relationship of strain and displacement of the shaft. In order to emphatically study the shaft’s nonlinear bending vibration, the tensional and torsional deformations were ignored. Thus, the nonlinear bending vibration equations for the rotating composite thin-walled shaft were obtained considering the external and internal viscous dampings. Galerkin’s method was used to discretize the governing equations and the ordinary differential equations of the rotating shaft hending vibration were obtained. By using the fourth-order Runge-Kutta method, the differential equations were integrated numerically in time domain, the displacement-time responses, phase plane curves and power spectra of the shaft were obtained. The effects of external damping, internal damping, mass eccentricity and rotating speed on the nonlinear bending vibration responses of the shaft were studied. The numerical simulation results showed that the shaft may exhibit a chaotic motion.
Key words:nonlinear vibration; composite thin-walled shaft; rotating shaft
复合材料由于比强度和比刚度高、抗疲劳和减振性能好,在直升机尾传动轴[1]以及汽车传动轴[2]的结构设计中已经显示出广阔的应用前景。采用复合材料取代金属材料不仅可以减轻结构的重量,同时还能够减少噪声、提高结构的抗振性能。轻质复合材料轴通常具有细长、薄壁结构的形式,当复合材料轴的长度增加时,其变形的几何非线性特征也会随之显现出来。
不计几何非线性的复合材料轴的线性振动问题的研究,一般仅限于对固有频率和临界转速进行求解和稳定性分析,但是无法对复合材料轴在不平衡激励下的非线性响应进行分析和预测。因此,需要借助于非线性振动的理论揭示复合材料轴的非线性动力行为。
文献[3-7]关于旋转轴的几何非线性动力学问题的分析与建模仅限于针对各向同性实心轴;文献[8]虽然给出了一个计及几何非线性的复合材料薄壁梁的非线性振动模型,但是其中没有考虑旋转效应而且也未能给出有关非线性振动特性的数值结果;文献[9-10]研究了结构非线性变形的复合材料薄壁旋转梁的动态特性,但是所建立的动力学方程仅适合于叶片类旋转复合材料结构而不适合于旋转复合材料轴。目前尚未见到计及几何非线性的旋转复合材料薄壁轴非线性振动的研究报道。
本文以变分渐进法(VAM)薄壁梁理论为基础[11],通过引入Von Kármán几何非线性,采用Hamilton原理和Galerkin法建立了一个复合材料薄壁轴的非线性振动分析模型。将本文模型和计算方法用于周向均匀刚度(CUS)(即满足:θ(y)=θ(-y),θ(z)=θ(-z),式中,θ表示由正向s轴进行度量的纤维铺层角)复合材料薄壁轴的横向非线性振动分析,其中考虑了质量偏心、外阻和内阻的影响。研究结果表明,本文提出的模型和计算方法能够用于分析和预测具有几何非线性的复合材料薄壁轴的振动特性以及包括轴的偏心、外阻、内阻和转速等主要参数对非线性动力学行为的影响规律。
1振动微分方程的建立
具有圆形截面、长度为L的复合材料薄壁轴,以不变角速度Ω绕转轴旋转。定义轴的旋转坐标系(x,y,z)和固定坐标系(X,Y,Z),它们具有共同的原点,此外还定义局部坐标系 (x,s,ζ),如图1所示。
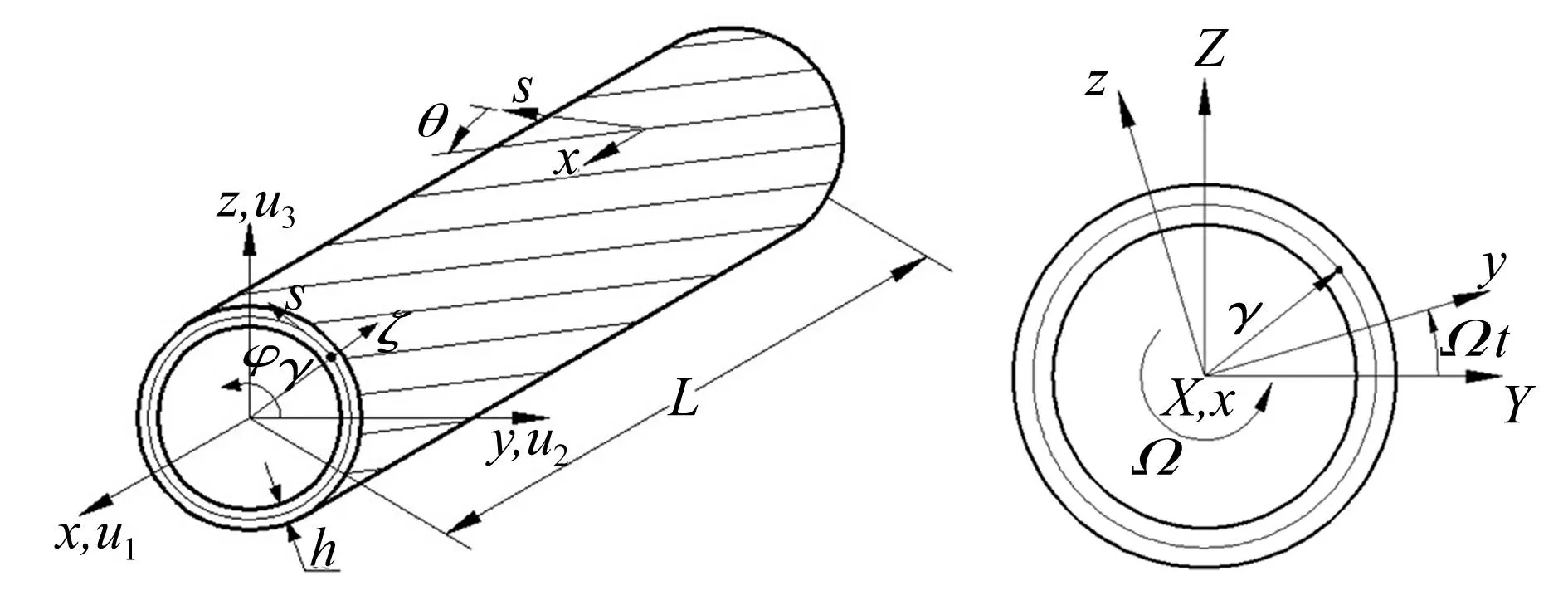
图1 圆截面复合材料薄壁轴 Fig.1 Thin-walled composite shaft of a circular cross section
为了导出复合材料薄壁轴的非线性振动方程,利用Hamilton原理
(1)
其中:U和T分别为应变能和动能,分别表示如下

(2)
(3)
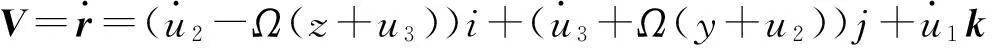
如果在位移应变关系中考虑Von Kármán几何非线性,可以推出[10]

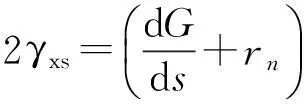
(4)
其中:G(s)的物理意义为扭转率,g1(s)的物理意义为轴向应变,g2(s)和g3(s)的物理意义为沿y,z方向的弯曲曲率;φ表示横截面绕x轴的扭转角。
应力应变本构关系
(5)

将式(5)代入(2),进行变分,得[10]
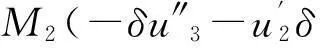
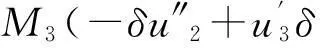
(6)
其中:F1,M1,M2,M3表示轴的广义截面内力和力矩,其具体表达式见文献[10]。
动能的变分为
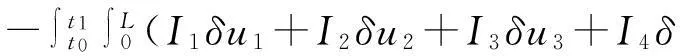
(7)
将式(6)、(7)代入变分方程 (1),得
(8)
其中:
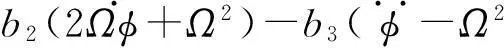

(9)

b1=∬AρdA,b2=∬AρydA,b3=∬AρzdA,
b4=∬Aρy2dA,b5=∬Aρz2dA
为了求得复合材料轴横向非线性振动的近似解析解,在方程组(8)的第二、三个方程中忽略轴向变形和扭转变形,并且考察具有CUS构型的圆形截面复合材料薄壁轴,得到横向振动的非线性动力学方程组
(10)
如果将坐标系置于固定坐标系下,并且同时考虑粘性外阻尼、内阻和偏心作用,则有[12]
(11)
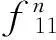
采用Galerkin近似求解方法,利用假设振型消除轴的空间位置变量,将振动方程 (11)转化为关于时间的常微分方程。为了明确起见,假设轴的两端具有简支边界条件。
轴的弯曲变形表示如下
(12)
其中:弯曲振型函数选取标准的非旋转、非耦合、均匀简支梁的振型函数
(13)
为了着重研究第一阶模态的非线性动力学特性,对u2,u3取单模态近似,于是将(11)表示的非线性振动偏微分方程组,简化为2个未知函数U21,U31组成的非线性振动方程组
(14)
式中:
(15)
2算例分析
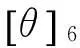
2.1外阻的影响

图2 不同外阻尼下的复合材料薄壁轴的位移响应 Fig.2 The time response of a composite shaft for different external damping coefficients
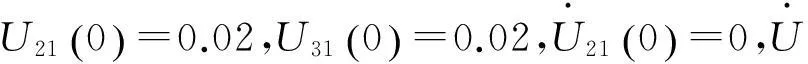
2.2内阻的影响
图3表示具有不同内阻的复合材料薄壁轴的时间响应曲线,取外阻尼cn=9 Ns/m。其他参数与图2的取值相同。结果表明,当cr=0.5 Ns/m时,轴的运动是稳定的,对应的时间响应曲线如图3 (a)所示。当cr=2 Ns/m时,轴的运动是临界稳定的,对应的时间响应曲线如图3(b)所示。当cr=4 Ns/m时,运动状态是不稳定的,轴的时间响应曲线如图3(c)所示。
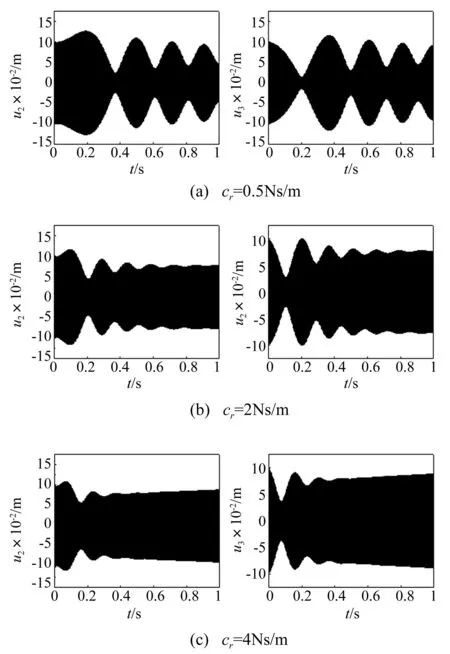
图3 不同内阻下的复合材料薄壁轴的位移响应 Fig.3 The time response of a composite shaft for different internal damping coefficients
数值结果还表明,在给定内阻的情况下,当转速逐步增加到达某个值时(Ω=2 500 rad/s),系统同样可以由稳定的运动变为不稳定的运动。为了节省篇幅,这些结果不再展示。
2.3偏心的影响
对应于四种不同的偏心距:即,e1=5×10-7m、e1=5×10-5m、e1=5×10-3m 和e1=5×10-1m,复合材料薄壁轴的动力学特性(包括时间响应图、相平面图和功率谱图)演化过程,分别如图4~7所示。所选取的参数分别为铺层角θ=60°,转速Ω=2 000 rad/s,偏心距e2=0,其他材料参数和初始条件同前。
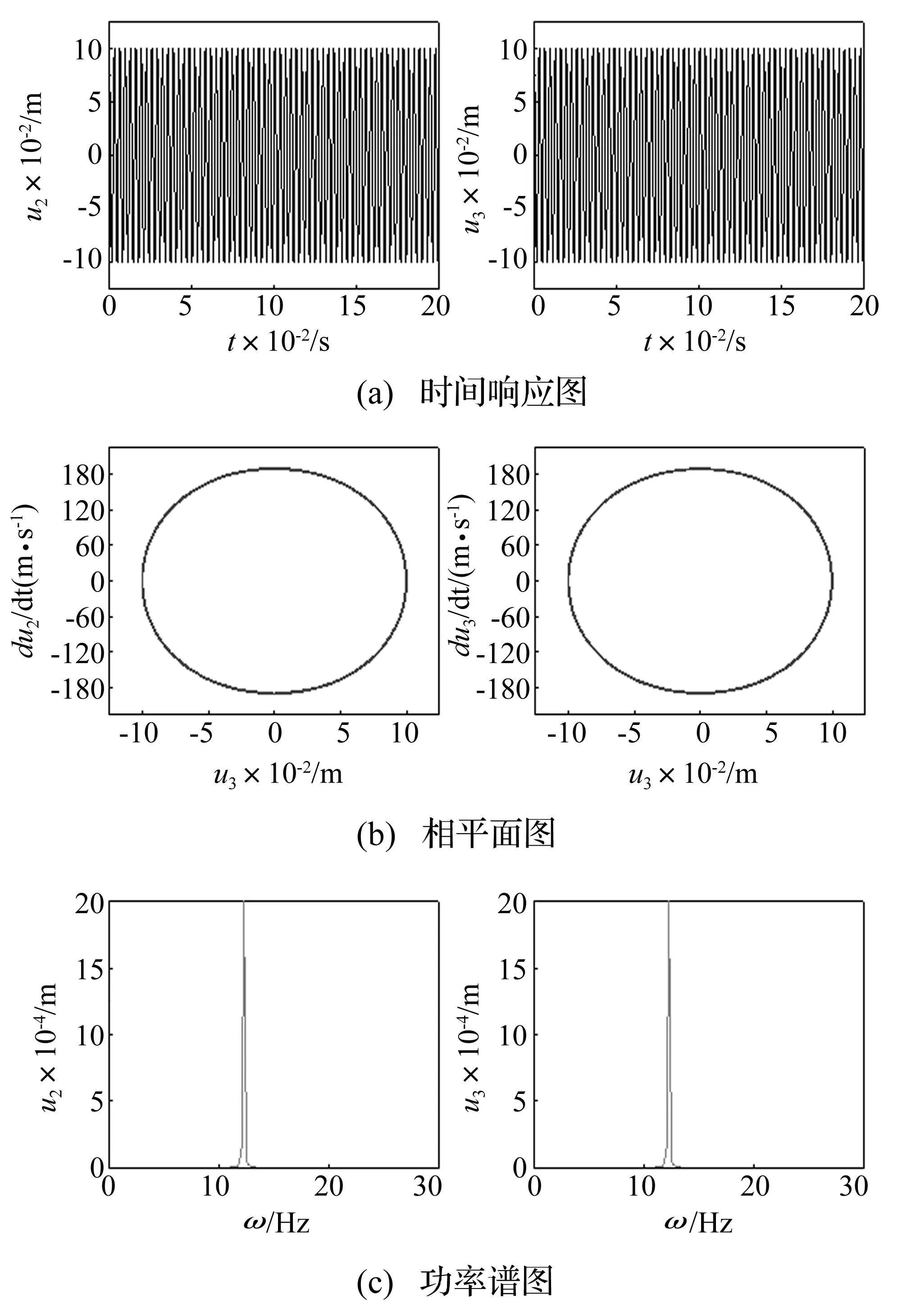
图4 单倍周期运动 Fig.4 Period-one motion of the composite shaft
结果表明,当e1=5×10-7m时,系统发生单倍周期运动,如图4所示;当e1=5×10-5m和e1=5×10-3m时,系统发生概周期运动,如图5和图6所示;当e1=5×10-1m时,系统发生混沌运动,如图7所示。
数值计算结果还显示出,除了偏心距之外,轴的转速对非线性振特性也有重要的影响。例如,在给定偏心距e1的情况下,随着转速的增加,轴的运动会依次表现为单倍周期运动、概周期运动、混沌运动、概周期运动和周期运动。为节省篇幅,这些图形不再给出。
2.4径厚比和长径比的影响
不计内外阻的影响,取径厚比分别为50,100和200,计算得到轴的时间响应图,结果表明,径厚比对响应幅值的影响很小,但是增加径厚比会导致固有频率有所增加; 此外,从长径比分别取20、60和100的计算结果看到, 固有频率随着长径比的增加显著增加, 而且长径比的增加也导致响应幅值明显增大, 为节省篇幅,这些图形也不再给出。

图5 概周期运动 Fig.5 Quasiperiodic motion of the composite shaft
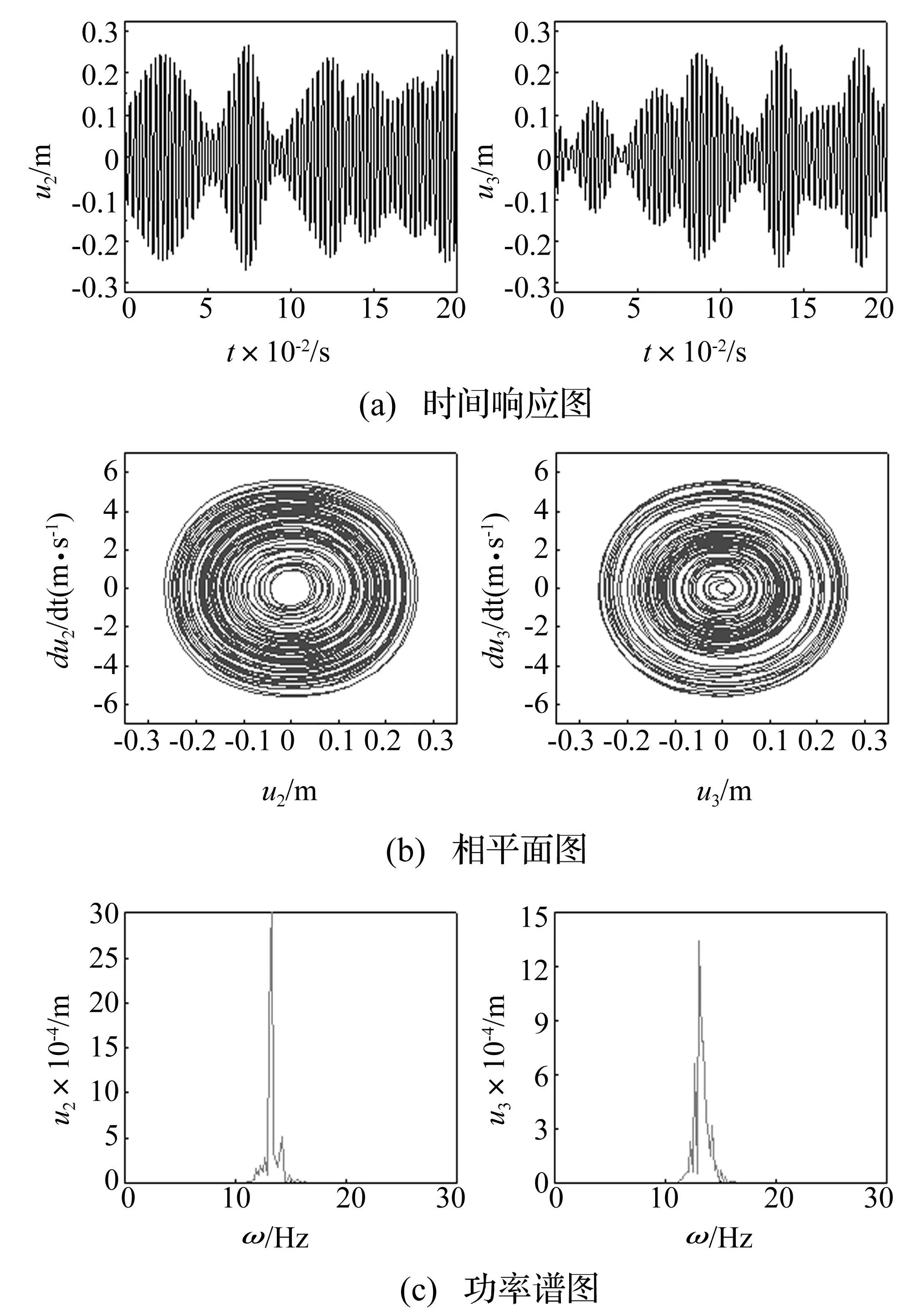
图6 概周期运动 Fig.6 Quasiperiodic motion of the composite shaft

图7 混沌运动 Fig.7 Chaotic motion of the composite shaft
3结论
提出了具有几何非线性的复合材料薄壁轴在不平衡激扰下的受迫振动分析模型,在不计拉-扭变形的影响的情况下,着重研究了横向弯曲非线性振动的响应特性。利用四阶龙格-库塔法对横向弹性变形耦合的系统模型进行数值分析。得到如下结论:
(1)随着偏心距的增大,轴将依次出现单倍周期运动、概周期运动和混沌运动;类似地,随着转速的增大,轴也会依次表现出单倍周期运动、概周期运动、混沌运动、概周期运动和单倍周期运动。
(2)外阻尼对轴的振动只产生抑制作用,振动抑制的效果随着外阻尼的增加而增加。然而,内阻会降低轴的动力稳定性。在转速固定的情况下,随着内阻的增加,轴的运动由稳定状态逐渐变为不稳定状态;在内阻固定的情况下,随着转速的增大,轴的运动状态同样可由稳定逐渐变为不稳定。
参考文献
[1]王震鸣,杜善义,张衡,等.复合材料及其结构的力学、设计、应用和评价(第二册)[M].哈尔滨: 哈尔滨工业大学出版社,1998.
[2]Hetherington E L, Kraus R E, Darlow M S. Demonstration of a super critical composite helicopter power transmission shaft[J]. Journal of American Helicopter Society,1990,35(1):23-28.
[3]Shaw J, Shaw S W. Non-linear resonance of an unbalanced rotating shaft with internal damping[J]. Journal of Sound and Vibration,1991,147:435-451.
[4]Ishida Y, Nagasaka I, Inoue T, et al. Forced oscillations of a vertical continuous rotor with geometric nonlinearity[J]. Nonlinear Dynamics, 1996, 11:107-120.
[5]陈予恕,丁千. 非线性转子动力学的稳定性和分岔[J]. 非线性动力学学报,1996,3(1):13-22.
CHEN Yu-shu, DING Qian. A Study on stability and bifurcation of nonlinear rotor dynamics [J]. Journal of Nonlinear Dynamics, 1996, 3(1):13-22.
[6]Hosseini S A A, Khadem S E. Analytical solution for primary resonances of a rotating shaft with stretching non-linearity[J].Journal of Mechanical Engineering Science,2008,222:1655-1664.
[7]Shahgholi M, Khadem S E. Primary and parametric resonances of asymmetrical rotating shafts with stretching nonlinearity[J]. Mechanism and Machine Theory, 2012,51:131-144.
[8]Bhaskar K, Librescu L. A Geometrically non-linear theory for laminated anisotropic thin-walled beams[J].International Journal of Engineering Science, 1995, 33 (9):1331-1344.
[9]石庆华,向锦武.大变形薄壁复合材料旋转梁静动态特性分析[J]. 工程力学, 2008,25(1):86-91.
SHI Qing-hua, XIANG Jin-wu. Static and dynamic analysis for composite rotating beams using large deformation theory[J]. Engineering Mechanics, 2008,25(1):86-91.
[10]任勇生,代其义,孙丙磊,等.旋转几何非线性复合材料薄壁梁的自由振动分析[J]. 振动与冲击, 2013,32(14):139-147.
REN Yong-sheng, DAI Qi-yi, SUN Bing-lei, et al. Free vibration of a rotating composite thin-walled beam with large deformation[J]. Journal of Vibration and Shock, 2013,32(14):139-147.
[11]Berdichevsky V, Armanios E, Badir A. Theory of anistropic thin-walled closed-cross-section beams[J]. Composites Engineering, 1992,2:411-432.
[12]Genta G. Dynamics of Rotating Systems[M]. New York: Springer, 2005.