应用粒子群优化的高斯粒子滤波

戴曼娜，林培杰，程树英，苏诗荐，郑柏春

(福州大学微纳器件与太阳能电池研究所，福建福州 350116)

0 引言

高斯粒子滤波(Gaussian particle filtering，GPF)是一种免重采样粒子滤波算法，通过蒙特卡罗方法直接获取分布的估计均值和协方差，避免了重要性重采样带来的样本贫化问题，改善了算法的收敛特性和并行实现，在非线性系统中应用广泛［1－2］．但由于高斯粒子滤波是假定在贝叶斯最优估计框架下滤波的，预测概率分布采用单峰高斯分布，当真实后验分布为多峰分布时，单峰高斯假设就不能满足贝叶斯估计精度．与其他粒子滤波理论相似，GPF算法只给出了基本的滤波框架，具体的实现方法多种多样．2003年，Kotecha等［3］首次提出GPF的概念，并给出相应的实现框架．Wu、Hu等［4］提出半高斯滤波算法，改进了GPF的结构．Yang和Zhou［5］以及Kotecha等［6］对GPF进行改进，在一定程度上提高了滤波精度．

1995年，美国社会心理学家Kennedy和电气工程师Eberhart首次提出了粒子群优化(particle swarm optimization，PSO)算法［7－8］．这是一种有效的基于群体智能指导的迭代搜索最优解的全局寻优算法．该算法具有较好的初始种群鲁棒性，在算法初始阶段收敛速度快，且实现简单，需调整的参数较少，得到的最优解精度较高．近年来，国内外专家学者对PSO算法的研究逐渐深入，在工程应用方面［9－12］研究颇多．

针对高斯粒子滤波的结构特点，提出一种新的基于粒子群优化算法的高斯粒子滤波算法(PSOGPF)，用于解决粒子退化问题和多峰分布情况下滤波精度下降的问题．PSO－GPF算法在GPF采样过程中，利用PSO算法引入最新的测量值，使得采样分布向高后验概率区域运动，改善了粒子群之间的信息交流，提高了多峰分布情况下的估计精度．考虑到经典的PSO算法会陷入局部最优，因此，在经典的PSO算法中加入收缩因子促使粒子跳出局部极值，帮助算法在全局范围内找到最优值．同时，该算法选择高斯密度函数作为建议分布，不断更新粒子速度，化简滤波结构，解决粒子退化的问题，其收敛性好于经典的PSO算法．经测试，该算法能提高高斯粒子滤波的精度和稳定性，有效改善高斯粒子滤波的滤波性能．

1 高斯粒子滤波算法

高斯粒子滤波算法通过高斯密度函数来近似状态后验概率密度函数和预测概率密度函数．其基本思想就是从目标状态的先验概率密度函数中抽取N个带权值的样本{xik，wik}Ni=1，通过回归递推来求解后验概率密度函数的均值和协方差．同时，高斯粒子滤波中测量更新和预测更新所使用的粒子群是经过高斯采样得到．由于初始粒子群可以在程序运行前事先得到，因此，高斯粒子滤波中的初始粒子群生成过程不会对算法的实时性产生较大影响．同时，这也为使用复杂度更高更精确的高斯采样算法生成初始粒子群提供了方便．此外，在每次迭代滤波时都要重新产生采样粒子，所以不会出现由于迭代次数不断增加而造成的一般粒子滤波器存在的“粒子退化”问题，避免了一般粒子滤波器所需要的二次采样过程．

2 带压缩因子的PSO算法

2．1 基本的PSO算法

PSO算法的整个过程可以表述为:随机初始化一个粒子群，粒子总数为N，其中第i个粒子在d维空间的位置表示为Xi=(xi1，xi2，…，xid)，速度表示为Vi=(vi1，vi2，…，vid)．每一次迭代时，粒子通过两个极值来更新自己的速度和位置．将粒子从初始到当前迭代为止搜索产生的最优适应度值作为个体极值Pbest，记为Pi=(pi1，pi2，…，pid)．将种群目前为止的最优适应度值作为全局极值Gbest，记为G=(g1，g2，…，gd)，而Gbest为Pbest的最优．在找到这两个最优适应度值后，用公式(1)和(2)来分别对第t+1次迭代时第i个粒子第j维的速度vij(t+1)和位置xij(t+1)进行更新:

下式中隐含了单位时间为1 s，根据公式:距离=时间(1 s)×速度，可以根据公式(2)，利用速度进行位置更新:

其中:Rand是介于(0，1)的均匀分布随机数;w称为惯性系数;c1和c2是正的学习因子．粒子群优化算法通过计算适应度值将所有的粒子向最优粒子移动．适应度函数fitness定义如下:

其中:Rk是测量噪声方差;zNew和zPred分别是最新测量值和预测测量值．

2．2 带压缩因子的PSO算法

学习因子c1和c2决定了粒子本身经验信息和其他粒子的经验信息对粒子运行轨迹的影响，反应了粒子群之间的信息交流．c1较大，会使粒子过多地徘徊在局部范围内;c2较大，又会使粒子过早收敛到局部最小值．

引入了压缩因子的PSO算法可以有效地控制粒子的飞行速度，有效地平衡了粒子的全局探测与局部开采之间的关系，其速度和位置的更新公式为:

压缩因子f按下式计算:

为保证算法的顺利求解，c1+c2必须大于4．

带压缩因子的PSO算法的具体实现流程如下:

Step 1 随机初始化种群中粒子的位置和速度;

Step 2 根据公式(3)计算每个粒子的适应度，将当前各粒子的位置和适应度存储在各粒子的Pbest中，选取出所有Pbest中适应度最优个体，将其位置和适应度存储在Gbest中;

Step 3 根据公式(4)、(5)、(6)和(7)更新粒子的速度和位置;

Step 4 将每个粒子的适应度值与其经历过的最好的位置的适应度值做比较;如果粒子当前的适应度值较好，则将其作为该粒子的个体历史最优值，粒子的当前位置作为个体的最好位置;

Step 5 比较当前所有Pbest和Gbest值，更新Gbest值;

Step 6 若满足停止条件(一般情况下采用预设的运算精度或者最大迭代次数)，搜索停止，输出结果;否则返回Step 3，继续搜索最优值．

3 PSO－GPF的改进之处及具体步骤

3．1 PSO－GPF的改进之处

1)常规的粒子滤波采用了次优的重要性函数，因此，粒子的重要性采样过程是次优的．同时，多峰分布情况下，存在高斯粒子滤波估计精度问题．为了优化高斯粒子滤波的采样过程，改善估计精度，本研究将PSO算法融入到高斯粒子滤波中．

2)PSO算法中引入压缩因子，能有效解决粒子的全局探测和局部开采的平衡问题，最大化地提高粒子的使用效率．

3)将高斯分布作为建议分布，以化简滤波结构，减小了粒子退化问题．

3．2 PSO－GPF的具体实现步骤

Step 1 取得测量值:

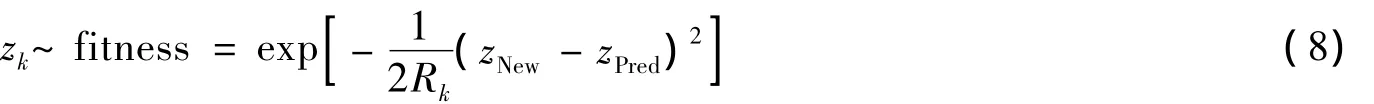
式(8)中，Rk是测量噪声方差，zNew和zPred分别是最新测量值和预测测量值;

Step 2 初始化种群中粒子的位置和速度;

Step 4 测量更新:根据公式(3)计算每个粒子的适应度，将当前各粒子的位置和适应度存储在各粒子的Pbest中，选取出所有Pbest中适应度最优个体，将其位置和适应度存储在Gbest中;

Step 5 根据最优值并利用式(4)～(7)更新每个粒子的速度和位置，使得粒子不断向真实状态靠近;

Step 6 比较每个粒子的适应度值与其所经过的个体历史最好位置的适应度值，如果更好，则将其作为粒子的个体历史最优值，粒子的当前位置作为该粒子的个体历史最好位置;

Step 7 比较当前所有Pbest和Gbest值，更新Gbest值;

Step 8 若满足停止条件(一般情况下采用预设的运算精度或者最大迭代次数)，搜索停止，输出结果;否则返回Step 5，继续搜索最优值;

Step 10 利用公式计算每个粒子的权重:

Step 11 根据公式归一化每个粒子的权重:

Step12 估计滤波分布的均值μk、协方差，以及双高斯和的权值al，即

4 仿真结果与分析

应用GPF算法和PSO－GPF算法分别对一维非线性模型进行仿真，系统的离散状态方程和测量方程定义如下:

该系统为似然函数呈双峰的高度非线性系统，传统的滤波方法难以处理该系统．下面分别用GPF和PSO－GPF进行状态估计跟踪．

为了显示PSO－GPF中粒子的搜索空间维度D和最大迭代次数DT，max对实验改进结果的影响，特将除了两者以外的其余参数进行统一设置，以保持实验环境的一致性．这些参数设置如下:令GPF和PSOGPF的过程噪声方差Q=10，观测噪声方差R=1，初始估计方差P=5，时间步长tf=50 s;设置GPF的采样粒子数目N=100;设置PSO－GPF的参数为:采样粒子数目Np=30，学习因子c1=2．8，学习因子c2=1．3，时间间隔1 s，目标初始状态为x0=0，双高斯和初始权值a1=a2=0．5．

PSO算法中，对于一般的优化问题，粒子数取20至40已可解决大部分问题并取得不错的结果．对于比较难的问题或者特定类别的问题，粒子数可以取到100以上．对于本实验，在对PSO－GPF的参数进行设置时，设定采样粒子数目Np=30和Np=100．

学习因子c1和c2通常取2，但也可取其他的值，一般c1和c2相等，且范围在0至4之间．本实验中，为了防止粒子过早收敛到局部最小值，故将c2设置得较小．同时，为了确保C大于4，故设置c1=2．8，c2=1．3，此时 C=4．1，压缩因子为 0．729。

1)令PSO－GPF的采样粒子数目Np=30、搜索空间维度D=30、最大迭代次数DT，max=100，GPF和PSO－GPF的滤波结果和估计值误差分别见图1和图2．

图1 在N p=30、D=30和D T，max=100条件下，不同算法的滤波结果比较Fig．1 Comparison of results among different filtering algorithms under N p=30，D=30 and D T，max=100

图2 在N p=30、D=30和D T，max=100条件下，不同算法的估计值误差的比较Fig．2 Comparison of the estimate errors of different algorithms under N p=30，D=30 and D T，max=100

为了进一步比较GPF和PSO－GPF在估计误差方面的性能，引入均方根误差(root mean square error，RMSE)作为评价指标．均方根误差计算公式为:

表1给出了不同滤波算法的RMSE和所用的运行时间，实验在Windows XP平台上用Matlab编程实现．可以看到，在Np=30、D=30、DT，max=100时，PSO－GPF比GPF的精度提高很多，达到了98．6%．

表1 在N p=30、D=30和D T，max=100条件下，不同滤波算法的滤波结果数据比较Tab．1 Comparison of filtering data among different filtering algorithms under N p=30，D=30 and D T，max=100

2)令PSO－GPF的采样粒子数目Np=30、搜索空间维度D=40、最大迭代次数DT，max=200，GPF和PSO－GPF的滤波结果和估计值误差分别见图3和图4．

图3 在N p=30、D=40和D T，max=200条件下，不同算法的滤波结果比较Fig．3 Comparison of results among different filtering algorithms under N p=30，D=40 and D T，max=200

图4 在N p=30、D=40和D T，max=200条件下，不同算法的估计值误差的比较Fig．4 Comparison of the estimate errors of different algorithms under N p=30，D=40 and D T，max=200

表2给出了在Np=30、D=40、DT，max=200时，GPF和PSO－GPF算法的RMSE和所用的运行时间．可以看到，PSO－GPF比GPF的精度提高很多，达到了74．3%．与Np=30、D=30、DT，max=100时相比，GPF和PSO－GPF算法各自的RMSE值变化不大，但PSO－GPF比GPF的精度提高率略有下降．说明在参数设置为Np=30、D=30、DT，max=100时，已可达到很好的精度，且减小D和DT，max的设置还可缩短PSO－GPF的运行时间．

表2 在N p=30、D=40和D T，max=200条件下，不同滤波算法的滤波结果数据比较Tab．2 Comparison of filtering data among different filtering algorithms under N p=30，D=40 and D T，max=200

3)为了进一步比较PSO－GPF中采样粒子数目Np对PSO－GPF算法的影响，在图1和图2的参数设置下，只改变PSO－GPF采样粒子数目为Np=100．GPF和PSO－GPF的滤波结果和估计值误差分别见图5和图6．

由图5和图6可以看出，当采样粒子数均为100时，PSO－GPF比GPF的估计精度高，表3显示PSO－GPF精度可提高93．9%．将表1和表3对比发现，采样粒子数Np的增加可以提高PSO－GPF的估计精度，但精度提高率不是特别明显，且算法的运行时间大大增加．因此，将参数设置为Np=30、D=30、DT，max=100时，能够更适应于实际应用的需要。

图5 在N p=100、D=30和D T，max=100条件下，不同算法的滤波结果比较Fig．5 Comparison of results among different filtering algorithms under N p=100，D=30 and D T，max=100

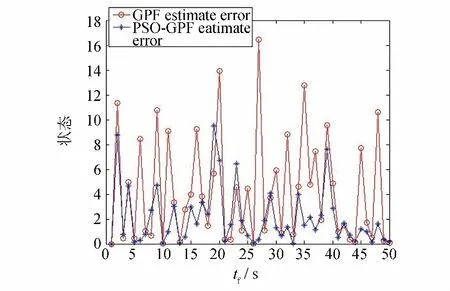
图6 在N p=100、D=30和D T，max=100条件下，不同算法的估计值误差的比较Fig．6 Comparison of the estimate errors of different algorithms under N p=100，D=30 and D T，max=100

表3在N p=100、D=30和D T，max=100条件下，不同滤波算法的滤波结果数据比较Tab．3 Comparison of filtering data among different filtering algorithms under N p=100，D=30 and D T，max=100

从以上图表可见，所设的PSO－GPF比GPF的估计精度高，所估计的结果更接近于真实的状态值，具有更好的稳定性．在粒子数目减小的情况下，用新的滤波方法对状态进行估计，其估计结果的准确性将比其他算法高，粒子滤波器的退化问题得以缓解．在图1和图3中，由于采用似然函数为双峰的非线性系统，GPF的滤波精度会受到影响．而PSO－GPF则利用了带压缩因子的粒子群优化算法，改善了滤波的采样过程，提高了样本的准确性，从而使滤波精度得到提高．与图2相比，图4中的PSO－GPF强化了粒子群的优化作用，扩大了粒子的维度，加大了算法的迭代次数，一般来说精度提高率应该更高，但由于PSO本质上是一种随机算法，在使用其他同样参数时，也可能得出不同的求解结果．所以，可以看到，图2中PSO－GPF的RMSE会比图4中的更小，精度更准确，这从表1～表2中可以直观地看到滤波精度提高的变化．图6与图2相比，加大了PSO－GPF的采样粒子数，可以一定程度提高PSO－GPF的估计精度，但考虑到精度提高率不是特别明显且运行效率变差，因此，将PSO－GPF参数设置成D=30、DT，max=100已可满足实际应用要求，且缩短了运行时间．

5 结语

提出一种新的应用粒子群优化的高斯粒子滤波方法，从优选重要性密度函数和优化滤波器采样效率的角度，来改善高斯粒子滤波在多峰分布情况下的精度问题和滤波器的退化问题．新算法采用粒子群优化算法产生高斯粒子滤波的建议分布参数，充分利用了最新观测数据，提高了滤波精度．同时，采用了带压缩因子的粒子群优化算法，用于控制粒子的全局探测与局部开采，减小了粒子陷入局部最优的可能性．此外，算法还应用高斯分布作为建议分布，能化简滤波结构，有效地减弱粒子退化现象．实验结果表明，改进的滤波算法具有较高的精度和稳定性，算法的精度提高可达到70%以上．