集值优化问题ε－强有效解的最优性条件

余丽

(宜春学院数学与计算机科学学院，江西宜春 336000)

0 引言

近年来，利用(次梯度)次微分刻画集值优化问题最优性条件已成为很多学者关注的热点问题．Tanino［1］引进了集值映射弱次微分的概念．基于Tanino的研究，很多学者相继提出了一些广义(次梯度)次微分的概念［2－4］，例如，点集映射的锥弱次梯度、锥－Henig有效次微分及超次梯度的概念，并在这些概念下，建立了一些最优性条件．

众所周知，有效解与最优性条件之间有着密切的联系．由于集值映射向量优化问题精确解的获得通常比较困难，因而逼近解是集值优化的重要组成部分．近年来，各种逼近解的概念相继引出，并得到了一些有趣的结果［5－7］．最近，Wang［6］研究了集值优化ε－强有效解的性质，能否将次微分的概念进一步推广并用于研究集值优化问题的逼近解?本文将在ε－强有效意义下对此问题进行讨论．

1 基本概念

设X为拓扑线性空间，Y和Z为Hausdorff局部凸的拓扑向量空间，Y*为Y的拓扑对偶空间．设φ≠S⊂Y，我们以cl S、int S和cone S分别表示S的闭包、内部和生成锥，其中cone S={λs:λ≥0，s∈S}．设C⊂Y为内部非空的闭凸点锥．凸子集B⊂C称为锥C的基，如果0∉cl B且C=cone B．C的对偶锥C*定义为C*={c*∈Y*:c*(c)≥0，c∈C}，这里c*(c)表示c*在c上的值．Bst={φ∈Y*:存在t＞0使得φ(b)≥t，b∈B}，称为基泛函．

定义1［7］设φ≠M⊂Y，ε∈C．点y∈M称为M关于锥C的ε－有效点，记为y∈ε－E(M，C)，如果M∩(y－C{0}－ε)=φ．

定义2［6］设B为C的基，N(0)是Y的零点邻域基，ε∈C．点y∈M⊂Y称为M关于锥C的ε－

Y强有效点，记为y∈ε－GE(M，C)．若∀φ∈Y*，∃U，V∈N(0Y)，使得φ［clcone(M+ε－y)∩(U－cone(V+B))］有界．

注1［6］在定义2中根据需要，U，V可以取为凸的对称邻域，且y∈ε－GE(M，C)，当且仅当∀φ∈Y*，∃U，V∈N(0Y)，使得φ［cone(M+ε－y)∩(U－cone(V+B))］有界．易知，ε－GE(M，C)⊂ε －E(M，C)．

引理1 设Y为局部凸的拓扑向量空间，序锥C是点凸锥，且有有界基B，ε∈C．如果φ≠M⊂Y，则:ε－GE(M，C)=ε－GE(M+C，C)．

证明 由定义2及文献［8］中引理1．3，易证．

设F:X→2Y是集值映射，则F的定义域，图和上图分别定义为

定义3［9］令F:X→2Y为一集值映射，(x0，y0)∈graph F．F称为在点(x0，y0)处是下半连续的，如果对y0的任意邻域N(y0)，存在x0的邻域N(x0)，使得对所有的x∈N(x0)，有F(x)∩N(y0)≠φ．

定义4［9］设集值映射F:X→2Y，如果对任意的x，x∈X，0≤λ≤1，有:

12

则称F在X上是C－凸的．

定义5 设F:X→2Y是集值映射，点∈ X，∈F()，并且φ*∈X*，给定向量p∈int C，若:

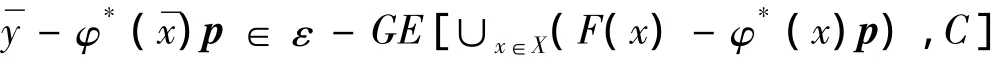
则称φ*∈X*是集值映射F在点关于向量p的ε－强有效次梯度．F在点关于向量p的ε－强有效次梯度的集合称为F在点处关于向量p的ε－强有效次微分，记作∂ε－GF．若∂ε－GF≠φ，则称F在点)关于向量p是ε－强有效次可微的．

2 ε－强有效次微分的存在性定理

引理2［3］设F:X→2Y是一集值映射，且x0∈dom F，则下面三个条件只要满足其中之一，就有int(epi F)≠φ．

1)存在y^∈F(x0)使得F在(x0，y^)处是下半连续的;

2)存在a∈Y，使得F(X)⊂a－C;

3)存在映射f:X→Y使得f(x)∈F(x)(∀x∈X)，并且f在x0的一邻域U(x0)内连续．

引理3［10］Bst具有以下性质:1)Bst≠φ;2)Bst⊂C*;3)若B是C的有界基，则Bst=int C*．

定理1 令B为C的有界基，(x0，y0)∈graph F，存在W^∈W(0)，使得y0∈ε－GE(F(x0)，CW^(B))．设F:X→2Y是CW^(B)－凸的集值映射，p∈int C，则只要引理2中的条件满足其中之一，就有 ∂ε－GF(x0，y0)p≠ φ．

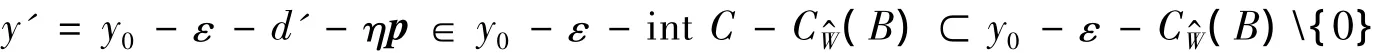
这样，y0∉ε－E(F(x0)，CW^(B))，因此，y0∉ε－GE(F(x0)，CW^(B))，此与已知矛盾，所以(x0，y0－ε)∉ int．由凸集分离定理知，存在(φ*，Ψ*)∈X*×Y*，(φ*，Ψ*)≠(0X*，0Y*)，使得:

即:

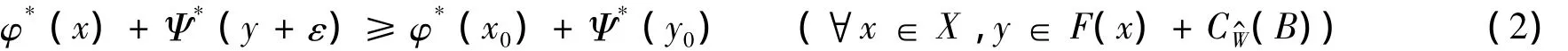
由于y+ε∈F(x)+CW^(B)+ε⊂F(x)+CW^(B)+CW^(B)⊂F(x)+CW^(B)，令y^=y+ε，则(2)式等价为:

下证Ψ*≠0Y*．若不然，则有φ*(x－x0)≥0，∀x∈X．对正实数λ＞0，任取v∈X，取x=±λv+x0，可得φ*(±λv)≥0．由此得到φ*=0X*，此与(φ*，Ψ*)≠(0X*，0Y*)矛盾．另一方面，在(3)式中取x=x0，=y0+q，∀q∈CW^(B)，有:ψ*(q)≥0，∀q∈CW^(B)．

由g≠0*及W^的吸收性得，存在s0∈W^W⊂C^(B)，使得g(s0)＜0．令t=－g(s0)，于是g(B)≥－g(s0)=t＞0．这就是g∈Bst．

下面证明若不成立，则由定义5及引理1知，存在φ∈Y*，使得对任意的U，V∈N(0Y)，有:

无界．取k＞0，δ＞0，使εt－δ＞0，令:

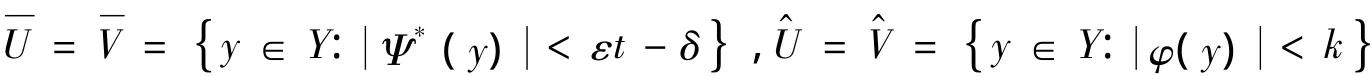
于是，存在λn＞0，xn∈X，yn∈F(xn)，cn∈C，μn≥0，un∈，vn∈，bn∈B使:

由(4)，(5)式可知存在一正整数N，使:

由Ψ*∈Bst，ε∈C知λnΨ*(ε)≥0，于是由(6)式得:

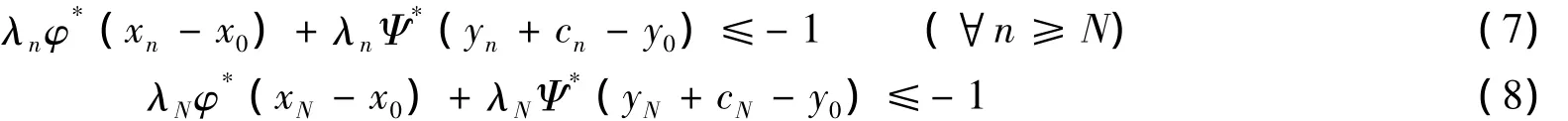
特别有:

由λN＞0及(8)式得:

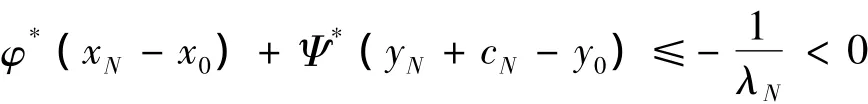
其中:(xN，yN+cN)∈epi F⊂，上式与(3)式矛盾．

有界．这等价于:φ［clcone(∪x∈X(F(x)－0(x－)p+ε－))∩(U－cone(V+B))］有界，因此0X*∈∂ε－GF，)p．

证明 必要性．由B为C的有界基及引理3知，存在t＞0，使Bst≠φ．设φ0∈Bst，由φ*∈∂ε－GF(，)p及引理1知，对上述的φ0∈Bst，∃U0，V0∈N(0Y)，使:

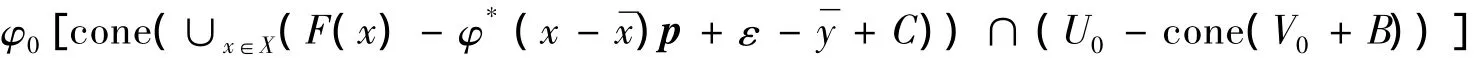
有界．由于F在X上是C－凸的，故∪x∈X(F(x)－φ*(x－)p+ε－+C)为凸集，于是cone(∪x∈X(F(x)－φ*(x－)p+ε－+C))是凸锥，于是，由文献［10］中定理2．2知，存在ξ∈(cone(v0+B))*及

由U－B是开凸集，则:

由 cone(∪x∈X(F(x)－ φ*(x－)p+ε－+C))是凸集知，clcone(∪x∈X(F(x)－φ*(x－)p+ε－+C))是凸集，由凸集分离定理知，存在Ψ*∈Y*{0Y*}使得:

由 clcone(∪x∈X(F(x)－ φ*(x－x)p+ε－y+C))是锥及Ψ*在其上有下界，得:

由0∈clcone(∪x∈X(F(x)－φ*(x－)p+ε－+C))及(11)式，得:

因为Ψ*≠0，则存在u0∈U，使得Ψ*(u0)=t＞0，在(13)式中取u0∈U，得ψ*(B)≥Ψ*(u0)=t即Ψ*∈Bst．由0∈C及(12)式，有:Ψ*(y－φ*(x－)p+ε－)≥0(∀x∈X，y∈F(x))，即:

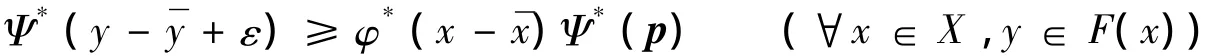
2)充分性．设存在Ψ*∈Bst，使(9)式成立．若φ*∉∂ε－GF(，)p，则存在φ1∈Y*，使得∀U，V∈N(0Y)，有:φ1［cone(∪x∈X(F(x)－ φ*(x－)p+ε－))∩(U－cone(V+B))］无界．取k＞0，δ＞0，令，则，，，∈N(0Y)．令 U~=V~=∩V^∈N(0Y)，对 U~，V~∈N(0Y)，存在

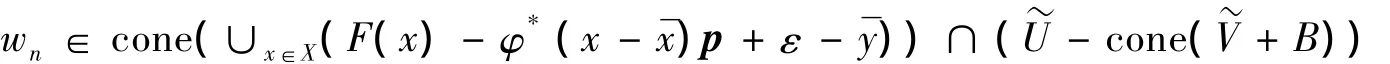
满足φ1(wn)→∞．将wn表示为:

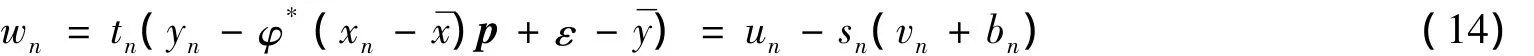
其中:tn≥0，sn≥0，yn∈F(xn)，un∈，vn∈，bn∈B．而B有界及φ1(wn)→∞，因此，sn→+∞．

由于Ψ*(b+v)＞t+δ－t＞0，∀v∈ V~，b∈B，于是存在n0，当n＞n0时，有:

于是Ψ*(tn(yn－φ*(xn－)p+ε－))＜0．由于tn≥0，故Ψ*(yn－+ε)＜ φ*(xn－)Ψ*(p)，此与(9)式矛盾．

3 稳定性

设Z为拓扑线性空间，Ω⊂Z是Z中半径为r的球．S:Ω→2X，F:X×Ω→2Y为两集值映射，考虑参

数扰动集值优化问题:

由参数优化问题的ε－强有效点集定义的集值映射如下:

定理4 令B为C的有界基，设F:X×Ω→2Y为C－凸的集值映射，S(q)为凸的集值映射．如果对任意的q∈Ω，F(S(q)，q)⊂ε－GE(q)+CW(B)．给定p∈int C，只要ε－GE(q)满足引理2中的一个条件，则对任意的q∈Ω，集值映射ε－GE(q)关于向量p是ε－强有效次可微的．

又因S(q)是凸的，所以:

因此，F(S(q)，q)在Ω上是C－凸的．

再注意到F(S(q)，q)⊂ε－GE(q)+CW(B)，所以就有:

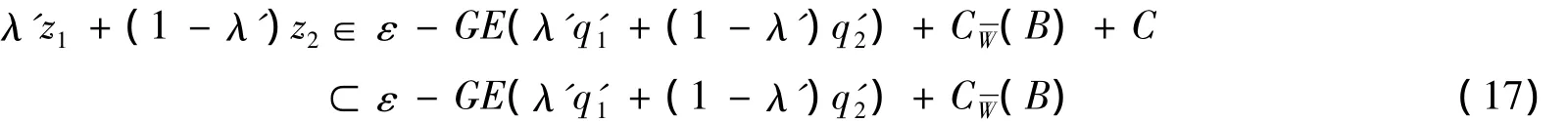
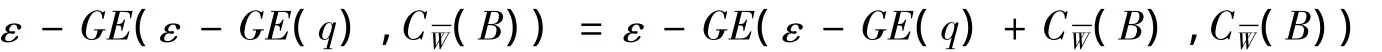
再利用F(S(q)，q)⊂ε－GE(q)+CW(B)，并且由假设ε－GE(F(S(q)，q)，CW(B))≠φ可知:

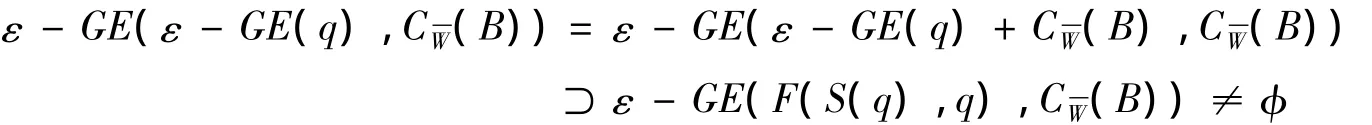
所以，集值映射ε－GE(q)满足定理1的条件，由此知结论成立．