具有非线性等式约束的故障诊断集员滤波器设计

阮玉镇，苗琳璐，王 武

(1．福建工程学院机械与汽车工程学院，福建福州 350118;2．福州大学电气工程与自动化学院，福建福州 350116)

0 引言

在控制界和信号处理界，故障诊断是动态系统的基本问题之一．因此，自1971年故障诊断技术产生以来，其研究得到了越来越多学者的青睐，目前依然是研究热点之一［1－3］．在一些实际应用系统，如化学处理过程［4］、目标跟踪［5］、投资问题［6］，其噪声分布未知但有界，且希望系统的状态能100%估计出．基于随机噪声的卡尔曼滤波方法［7］要求噪声分布已知，对系统状态的估计是点估计，无法估计出100%包含系统状态的界，因此无法胜任此类情况．集员滤波就是针对这类情况出现的一种滤波方法，它仅要求噪声约束界就能够保证被估计状态值在设计要求的范围内．基于这些优点，其应用涉及到很多领域，如电力系统［8］、机器人系统［9］、非线性系统［10］等．

针对实际工程中有状态约束的控制系统，许多学者提出研究状态约束问题的方法［11］．投影法是状态约束处理方法中研究最多、最普遍的一种方法，它的基本思想是首先获得一个没有约束的解决方案，然后将无约束的状态投影到有约束的状态约束表面，该方法克服了数值和空间问题，具有较强的可实现性，因此较多的文献都是采用投影法．

综上所述，针对具有状态约束的动态系统，采用投影法处理状态约束，选择集员滤波方法用于故障诊断，所设计的滤波器不仅能有效检测出故障，保证系统状态、故障在一定范围内，并且能判定出故障类型．

1 问题描述

考虑如下线性时变系统:

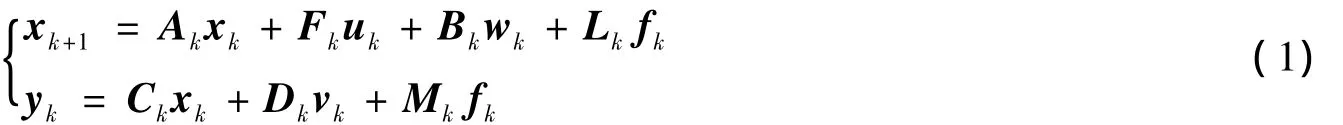
其中:xk∈Rn为系统状态，uk∈Rnu为已知输入，yk∈Rny为测量输出，Ak，Bk，Ck，Dk，Fk，Mk和Lk为已知的时变矩阵，wk∈Rnw为过程噪声，vk∈Rnv为测量噪声，fk∈Rnf为故障信号，分别属于超椭球集合:

其中:Qk=QTk＞0，Rk=RTk＞0和Sk=STk＞0为已知矩阵．系统的初始状态x0，f0满足超椭球集合约束:

其中:h(·)为非线性函数;dk为已知常数．

对于系统(1)，设计集员滤波器:

设计目标是对任意时刻k+1，具有非线性等式约束(4)的系统(1)，在给定过程噪声wk、观测噪声vk和故障信号fk有界的情况下，设计集员滤波器(5)，保证系统状态、故障信号100% 在超椭球界内，即系统状态、故障信号满足以下性能指标:

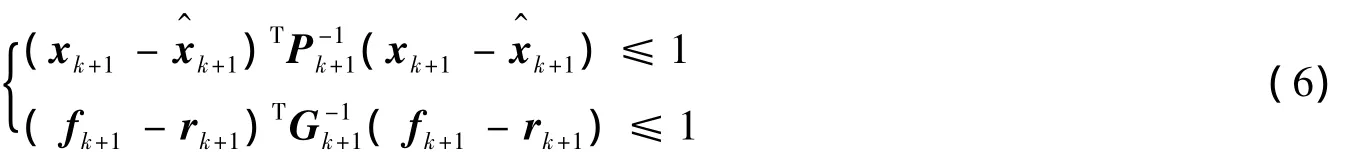
2 主要结果

定理1 针对具有非线性等式约束(4)的系统(1)，在任意k+1时刻，给定测量输出yk+1，如果:

1)过程噪声wk∈Wk、观测噪声vk∈Vk和故障信号fk∈Ψk;

2)xk和fk满足:(xk－)TP－1k(xk－)≤1，(fk－rk)TG－1k(fk－rk)≤1，其中，rk，Pk和Gk已知;

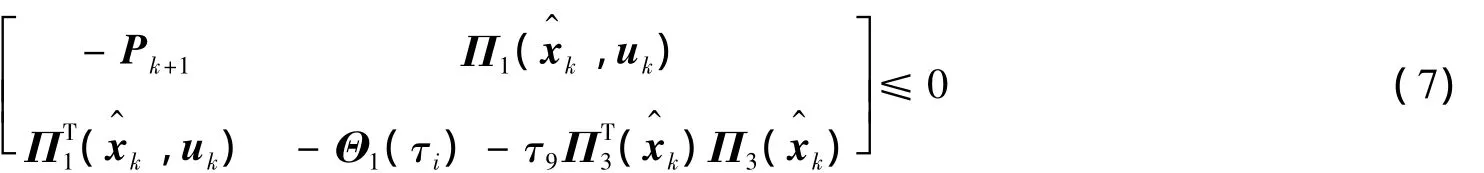
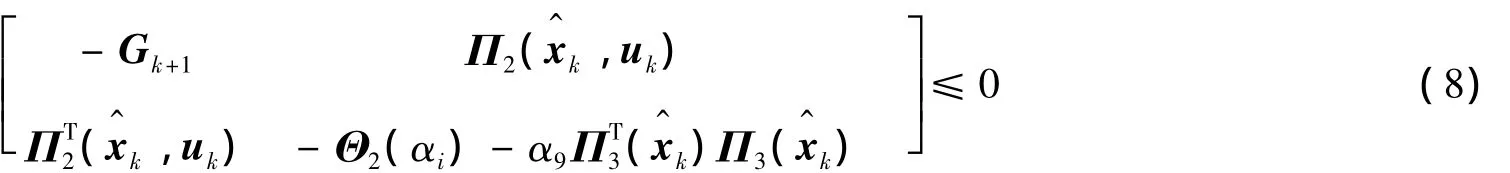
其中:

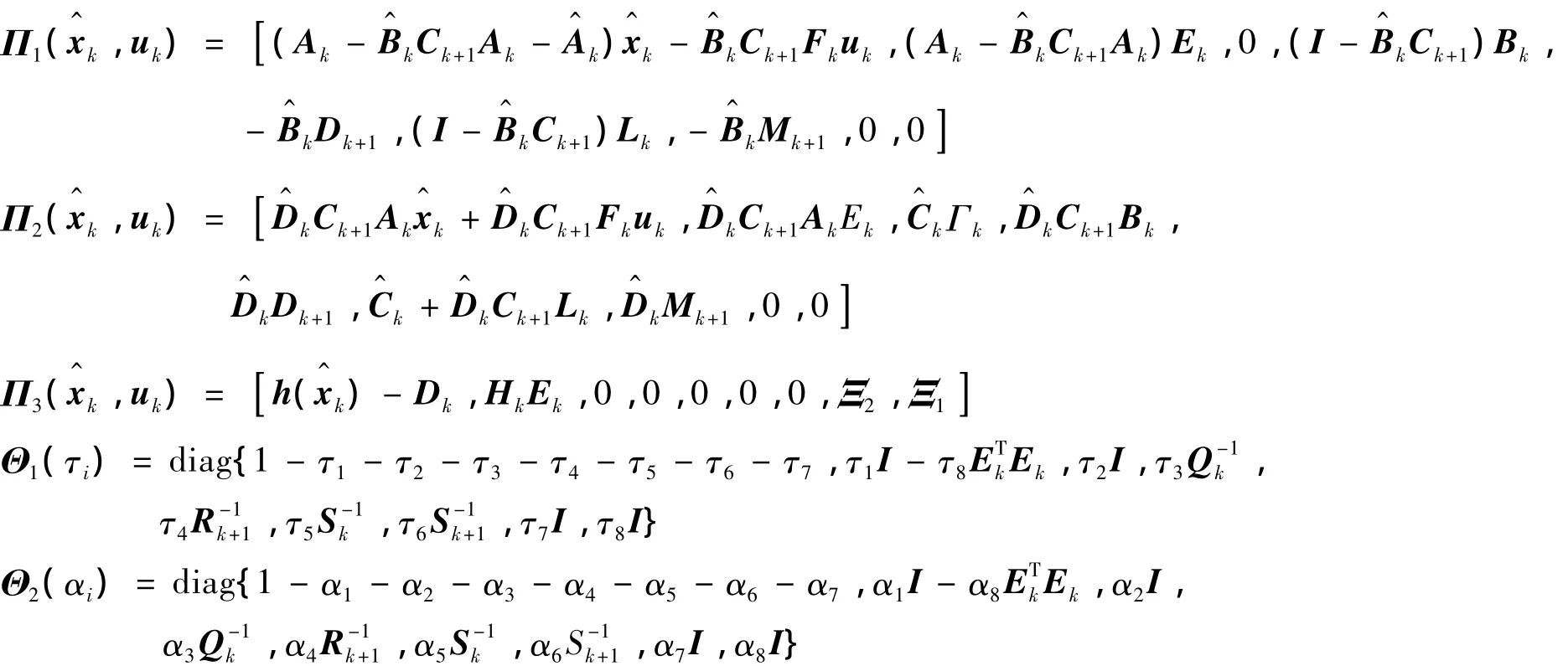
那么:①系统存在集员滤波器(5);②xk+1和fk+1满足式(6)，即保证系统的状态、故障信号100%包含在超椭球界内．

证明 假设在第k步时，系统状态xk和故障fk满足:

那么∃z，∃s满足 z≤1， s≤1，且存在矩阵Ek和Γk满足Pk=EkETk和Gk= ΓkΓTk，上述约束条件可转化为:

那么在k+1时，由式(5)和式(9)可得状态估计误差和故障估计误差分别为:

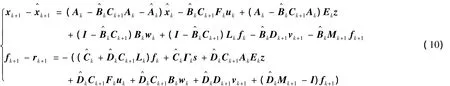
对非线性等式约束进行线性化，式(4)可写为

式中:Hk为雅克比矩阵;Ξ1和Ξ2是已知的标量矩阵;Δ1和Δ2是未知但有界的矩阵，且 Δ1≤1， Δ2≤1;Ξ1Δ1代表线性化过程基准点误差;Ξ2Δ2代表泰勒展开时高阶截断误差．代入式(9)，式(11)为:

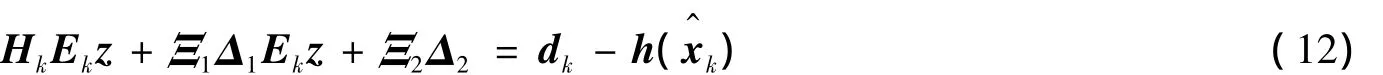
令Δ3=Δ1Ekz，那么式(12)为:

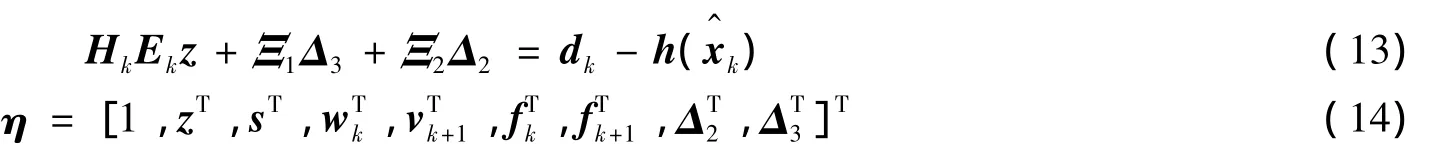
定义向量η为:

由式(10)，式(6)可写为:

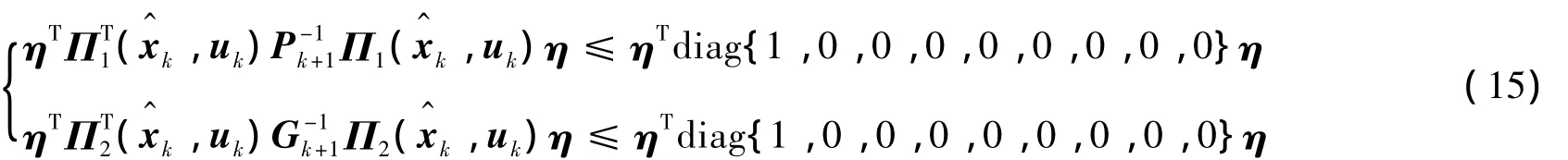
同理，式(13)可写为:

已知向量 z，s，wk，vk+1，fk，fk+1，Δ2和 Δ3满足:

将式(17)写成向量η的不等式形式，连同式(15)应用S－procedure引理，可得存在τi＞0，αi＞0，i=1～8使得式(18)成立．

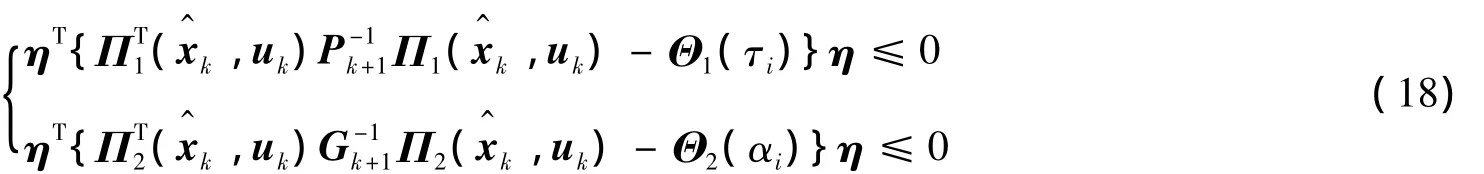
由式(16)和式(18)应用Finsler引理可得:

由Schur补引理可知，如果式(7)和式(8)成立，那么式(19)成立，即存在一个形如式(5)的集员滤波器，使得xk+1和fk+1满足式(6)．证毕．

注1 定理1给出了存在集员滤波器的LMI条件和集员滤波器参数设计方法．利用Matlab LMI Toolbox，解决如下凸优化问题，就可得到集员滤波器参数．

注2 根据文献［12］中给出的故障判别方法来进行故障检测．故障检测时，选取评价函数为:

其中:k0为初始评价时刻;L为评价步数．由于故障常常发生在有限时间段内，所以L是有限值．阈值的选取必须要考虑外界干扰的影响，为了尽量避免没有故障信号时出现误检测，而有故障信号时又要尽量迅速地检测出故障，取阈值函数为:

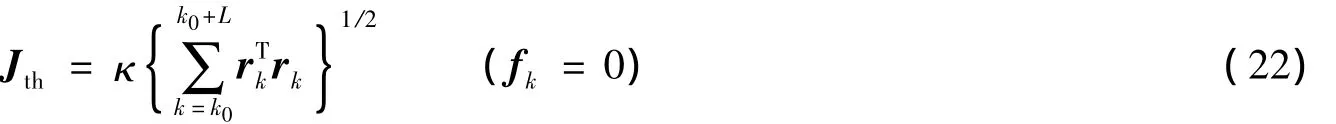
其中κ为阈值系数．通过计算每一时刻J(rk)和Jth的值来检测故障是否发生，即

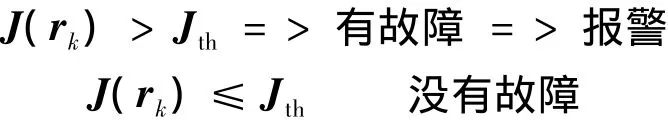
3 仿真研究

系统(1)参数如下:

其中:xk= ［xk1xk2xk3xk4］T，fk= ［fk1fk2］T．非线性状态约束为:(ζ+xk1)2+x2k2=ζ2

利用Matlab LMI Toolbox对优化问题(20)进行寻优，首先，假设同一时刻只有一个部件发生故障:

1)fk1，fk2，fk3和fk4取同种故障，且为正弦信号:

2)fk1，fk2，fk3和fk4取同种故障，且为方波信号:

图1和图2给出了在1)、2)故障情形下，状态变量xk1和xk2的真实值、估计值、上界线、下界线比较，无论故障为何种形式，只要故障信号的值有界，状态变量xk1和xk2100%在上下界内，满足性能要求．图3和图4分别是故障形式为1)、2)时的rk1估计值、上下界与真实值fk1比较图，图3和图4表明故障信号的估计值100%在上下界内，也满足性能要求，从故障波形图还可以判断出故障类型．

图1 x k1真实值、估计值、上下界Fig．1 The upper bound，the lower bound，the estimate and the true value of x k1

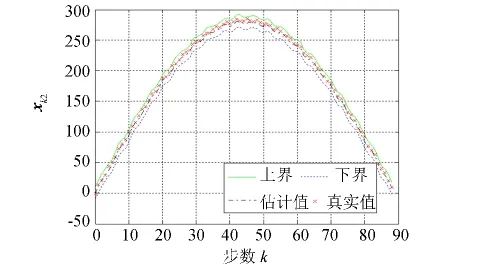
图2 x k2真实值、估计值、上下界Fig．2 The upper bound，the lower bound，the estimate and the true value of x k2

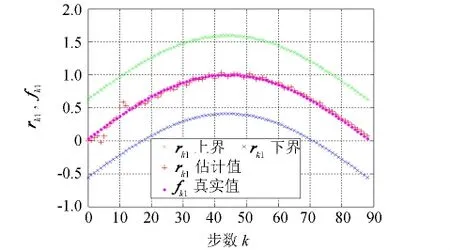
图3 故障为情形1)时，r k1与f k1Fig．3 Under the fault of case 1，the true value of f k1 and the estimate value of r k1

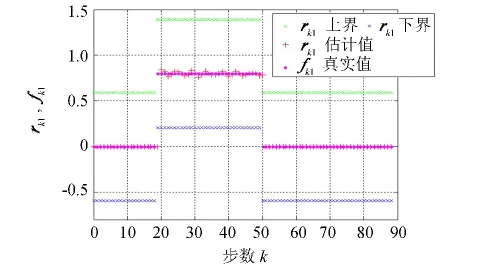
图4 故障为情形2)时，r k1与f k1Fig．4 Under the fault of case 2，the true value of f k1 and the estimate value of r k1

k2k1k2k1取κ=1．2，根据式(21)和式(22)计算每一时刻的残差评价函数值J(r)和阈值Jth，判断二者数值就可以检测出故障．通过仿真得到当k=24时，J(rk)=0．653 42＞Jth=0．144，说明故障在出现后第24步就可以被检测出来，如图6所示．

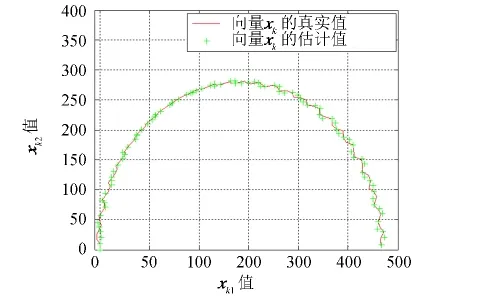
图5 x k1/x k2真实值与估计值Fig．5 The true and the estimate value of x k1/x k2

图6 故障为情形2)时，J(r k)和J thFig．6 The value of J(r k)and J thunder the fault of case 2

4 结论

针对具有非线性等式约束的线性时变系统提出了一种集员滤波器的设计方法，该方法保证系统状态、故障100%包含在上下界内．对非线性约束进行线性化并采用S－过程和Finsler引理得到集员滤波器存在凸条件，运用LMI方法就可求解所设计的集员滤波器参数．数值仿真表明，所设计的集员滤波器能100%估计出系统状态和故障的界，而且还能够辨别出故障类型，及时检测出故障．