剪力钉刚度对组合梁斜拉桥受力性能的影响研究

黄永辉，黄超凡，黄志科

(广州大学广州大学－淡江大学工程结构灾害与控制联合研究中心，广东广州 510006)

钢－混凝土组合结构是目前应用比较广泛的新型结构，充分利用了混凝土的抗压性能和钢结构的抗拉性能.为使二者能够更好结合充分发挥其性能，往往在钢与混凝土界面加入例如剪力钉之类的剪力连接件.剪力连接件主要传递结合面的剪力，抵抗其在剪力作用下的变形，对结构的刚度和受力将产生较大的影响［1］.钢－混凝土组合构件最早用于桥梁结构始于20世纪50年代［2］.钢－混凝土组合结构桥梁(简称组合桥)是指将钢梁与混凝土桥面板通过抗剪连接件连接成整体并考虑共同受力的桥梁结构形式［3］.相对于不按组合结构设计的纯钢桥，组合桥可以减小结构高度、提高结构刚度、减小结构在活载下的挠度.剪力连接件作为钢－混凝土组合结构的重要构件，其刚度对结构的影响受到了很多学者的关注与研究.DOGAN等［4］做了6组相同的剪力钉推出实验，对实验构件施加相同的周期荷载.实验发现在实验中剪力钉的刚度随着加载次数增加而逐渐减少.实验结果表明通过评估剪力钉的刚度退化能够预测钢－混凝土－钢叠合体系的在周期荷载下的使用寿命.同济大学的吴冲等［5］发现剪力钉通常受到双轴的剪力及由于行车荷载产生的横向弯矩，从而影响其受力性能.通过有限元方法分析了诸如剪力钉的高度、直径等参数对剪力钉受力性能的影响.发现了直径更大的剪力钉受双轴剪力的影响比较小，初始弯矩产生的混凝土裂缝对剪力钉的刚度是不利的.同济大学刘玉擎等［6］通过实验研究了单钉剪力连接件和多钉剪力连接件的受力性能区别，发现单钉剪力连接件与多钉建立连接件具有相近的刚度，多钉剪力连接件的钉间距离对刚度的影响很小.单钉的极限强度比多钉的大10%左右，当荷载达到峰值时单钉的相对滑移值比多钉的大19%左右.徐骁青等［7］提出了剪力钉的刚度过大会导致组合梁结构中钢与混凝土界面处的剪力的分布不均.为了解决这一问题，提出了用橡胶套裹住剪力钉以达到减小剪力钉刚度的效果.实验发现和未进行处理的剪力钉比较，处理过的剪力钉的抗剪强度变化不大可以忽略，但是剪力钉的刚度却明显的减小了，受剪力学性能也随之改变.综上可知，对于剪力钉的刚度研究大多集中在寻求影响剪力钉刚度的因素，而对于剪力钉刚度对组合结构受力性能影响的参数分析较少，本文研究了不同剪力钉刚度对组合梁斜拉桥的受力性能的影响，从而为该类结构设计提供指导.

1 工程背景

该背景桥为双索面独塔组合梁斜拉桥，其跨度为2×100 m，桥塔、主梁、桥墩固结，采用双柱式主塔，竖琴式双索面斜拉索，桥宽20.1 m，桥型布置图见图1.工字型钢梁作为主梁，横梁、小纵梁通过节点板连接形成钢构架，预制桥面板则架设在此钢构架上，采用现浇膨胀混凝土湿接缝，通过剪力钉将混凝土桥面板和钢主梁连接成一个整体.

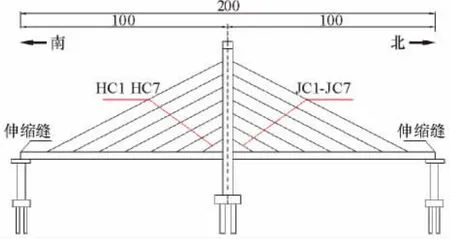
图1 某斜拉桥工程立面图/mFig.1 Elevation of the bridge/m

2 剪力钉滑移本构关系

在众多剪力钉荷载－滑移关系表达式中，OLLGAARD 等［8］提出的指数公式和 BUTTRY［9］的分数公式最具代表性，被广大研究者所引用.

OLLGAARD提出的剪力钉荷载－滑移关系表达式如下:

式中，Δ表示滑移量(mm);Q表示剪力值(kN);Qu表示抗剪承载力设计值(kN).

BUTTRY提出的剪力钉荷载－滑移关系表达式如下:

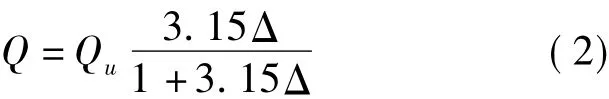
式中，Δ表示滑移量(mm);Qu为剪力钉的抗剪承载力设计值(kN).

OLLGAARD和BUTTRY公式曲线对比见图2，由图2可知，尽管表达式不一样，但两者曲线的相差并不大.

采用全曲线模型在有限元建模时较难实现，一般均采用分段式模型.为简化模型便于编程计算，有学者在实验的基础上提出了二折线或三折线模型来反映剪力钉荷载－滑移的非线性关系.其中最为经典的为 OEHLERS二折线模型和CHANG三折线模型.

OEHLERS等［10］提出的剪力钉二折线荷载－滑移本构曲线见图3.

图2 OLLGAARD和BUTTERY荷载－滑移曲线Fig.2 OLLGAARD and BUTTERY's Load-slip curves

弹性阶段的剪切刚度为

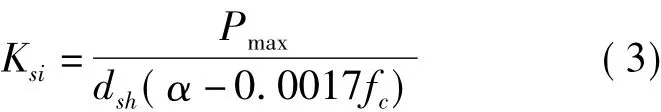
开始滑移点的滑移值为

极限滑移值为

式中，Pmax表示剪力钉抗剪强度设计值(N);dsh表示剪力钉栓杆直径(mm);fc表示混凝土抗压强度设计值(MPa);α取值范围为0.08～0.24.

CHANG等［11］提出的剪力钉三折线荷载－滑移本构曲线见图4.但曲线中关键点的数值没有给出理论计算公式，必须通过试验获得.

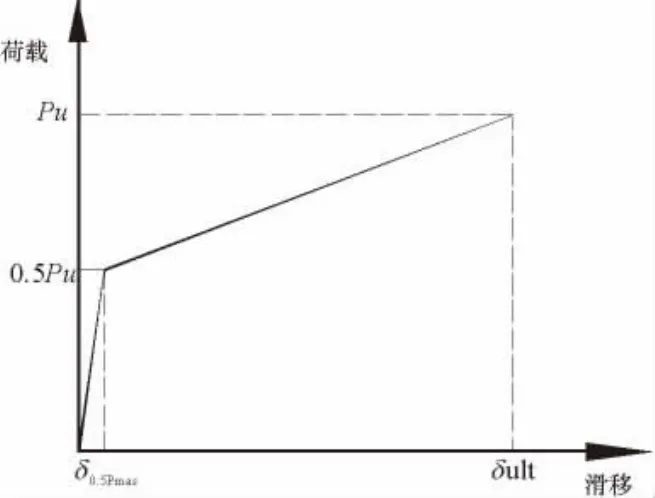
图3 OEHLERS荷载－滑移曲线Fig.3 OEHLERS's Load-slip curve

图4 CHANG荷载－滑移曲线Fig.4 CHANG's Load-slip curve

3 有限元模型的建立

采用ANSYS软件建立有限元计算模型，其中，桥塔采用梁单元beam188模拟，拉索单元采用桁架单元Link10模拟，主纵梁，小纵梁、横梁及桥面板均采用板壳单元shell63模拟，在钢纵梁与桥面板结合的位置采用非线性弹簧单元Combin39模拟剪力钉，板壳单元和弹簧单元采用共节点的方式连接.

Combin39是一个具有非线性功能的弹簧单元，具有轴向或扭转功能.轴向选项代表轴向拉压单元，每个结点具有3个方向的平动自由度.图5为Combin39单元的几何参数图.

由图5可知，可以采用分段直线来模拟剪力钉的荷载－滑移本构关系，因此，本文可采用OEHLERS方法来计算剪力钉的荷载滑移曲线.

图5 Combin39单元几何参数图Fig.5 Geometric parameters of Combin39

本次背景桥梁采用Φ22×200 mm剪力钉，各钢梁采用的剪力钉布置见图6，该桥共布置剪力钉49 754个.桥面板采用C50混凝土，其参数为Ec=34.5GPa，fc=23.1 MPa.

按OEHLERS方法计算可得，单个剪力钉的荷载－滑移曲线见图7.

图6 设计剪力钉布置图/mmFig.6 Layout of stud shear connectors/mm

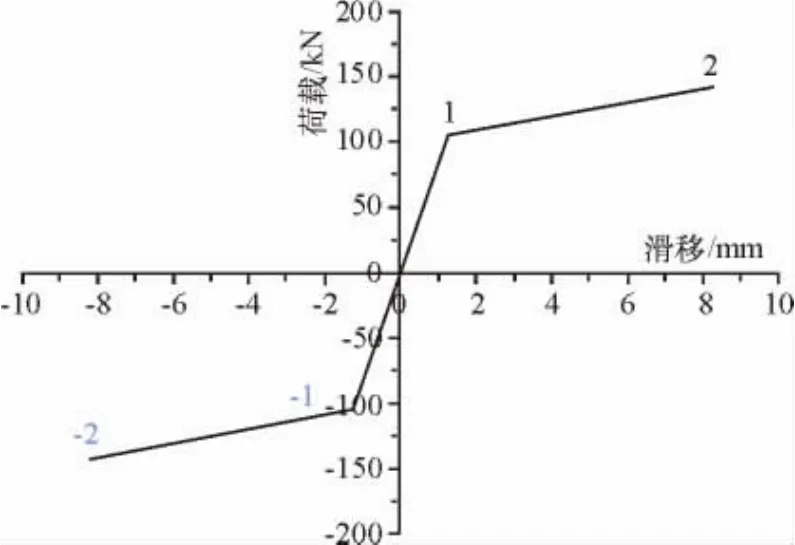
图7 单个剪力钉的荷载－滑移曲线Fig.7 Load-slip curve of single stud

为减小有限元模型的规模，从而提高计算速度，在建模时并不在所有剪力钉处划分节点，而是将单元段内的所有剪力钉等效为一个剪力钉，这样就减小了全桥模型的单元总数.剪力钉的等效刚度为

式中，nt为单元节段内剪力钉排数(横向)，nl为单元节段内剪力钉列数(纵向)，Ke为单个剪力钉的刚度.

按照以上方法，建立好的有限元模型见图8，加载示意见图9.

图8 算例桥梁有限元计算模型Fig.8 Finite element model of the bridge

图9 边界条件及加载方式Fig.9 Boundary conditions and load arrangement

在本文的有限元计算模型中，主要分析以下两种荷载工况:

(1)恒载工况:包括一期恒载和二期恒载;

(2)恒载+全桥均布车道荷载，右边跨跨中作用集中力.

4 参数分析

4.1 剪力钉刚度对界面滑移值的影响

采用结构在工况1作用下的结果来分析不同的剪力钉刚度对界面滑移值的影响，其界面滑移值对比见图10.由图可知采用不同刚度的剪力钉时，界面滑移值沿桥纵向的分布规律是基本一致的.当采用0.5倍设计刚度和1倍设计刚度计算时界面滑移值都较小，且二者数值相差也很小，最大滑移不超过0.3 mm.当刚度小于0.3倍的设计刚度时，由图可知滑移值会迅速变大，采用0.3倍设计刚度时最大滑移值为1.25 mm，采用0.1倍设计刚度时，最大滑移值为2.40 mm.

图10 界面滑移值曲线对比图Fig.10 Comparison of the interfacial slip curves

4.2 剪力钉刚度对位移的影响

不同剪力钉刚度模型对应的位移曲线见图11，由图可知桥梁模型的位移跟剪力钉刚度有着重要关系，剪力钉刚度的降低会使得桥梁的位移变大.当采用1倍设计刚度的剪力钉时，桥梁在工况1下的挠度最大值为0.18 m，当界面无剪力钉时，对应的最大挠度为0.22 m，挠度增幅达22.2%.

图11 位移曲线对比图Fig.11 Comparison of the displacement curves

4.3 剪力钉刚度对应力的影响

图12、图13分别为不同剪力钉刚度模型跨中截面的应变、应力图.由图12可知，随着剪力钉刚度的减小，其应变分布规律偏离平截面假定越大.如果完全不考虑界面的粘结滑移，那么钢梁底部拉应力为74.2 MPa，混凝土完全受压.当布置设计刚度的剪力钉时，钢梁底部拉应力为78.4 MPa，混凝土同样也是完全受压.当布置0.1倍设计刚度的剪力钉时，钢梁上缘的压应力区变大，最大压应力超过了拉应力，且混凝土板下缘出现拉应力，这样会大大削弱截面的整体刚度.由此可知，粘结滑移对组合梁桥应力分布有着非常重要的影响，剪力钉刚度对中和轴位置的影响同样十分明显，将导致钢梁出现受压，混凝土出现受拉的情况.设计时必须保证钢－混凝土界面有足够的粘结强度.

图12 沿梁高应变分布曲线Fig.12 Strain distribution curve along the height of the beam

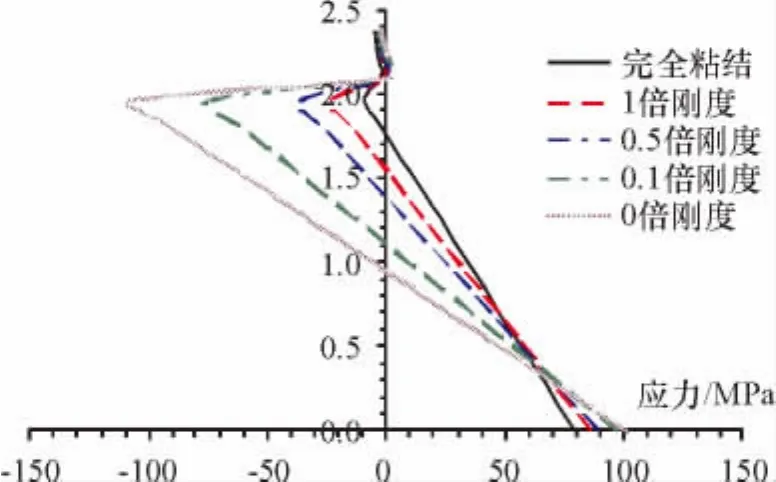
图13 沿梁高应力分布曲线Fig.13 Stress distribution curve along the height of the beam

4.4 剪力钉刚度对极限承载力的影响

因为作用在桥梁结构上的荷载往往十分复杂，很难用统一的荷载集度来表示，而结构的极限承载力跟荷载的形式有很大的关系，这就使得定义极限承载力指标变得较为困难.本文参考文献［12］，定义最大活载系数λmax和结构整体安全系数n2个参数来作为结构极限承载能力的指标.

不同剪力钉刚度模型的最大竖向挠度随荷载的变化曲线见图14.在工况2下的极限承载力计算结果见表1.

图14 不同剪力钉刚度模型最大挠度－荷载曲线Fig.14 The maximum deflection-load curve of the models with different stud stiffness

表1 工况2极限承载力计算结果对比Table 1 Calculation results of ultimate bearing capacity of the bridge in load case 2

由表1可知，考虑粘结滑移时，对于采用0倍设计刚度、0.1倍设计刚度、0.5倍设计刚度、1倍设计刚度的模型，其最大活载系数分别为不考虑滑移模型的54%，71%，84%和91%，其结构整体安全系数分别为不考虑滑移模型的60%，65%，86%和95%，以上结果说明剪力钉刚度对组合梁斜拉桥的极限承载力有着重要影响.当采用0倍设计刚度时即混凝土板和钢梁之间无剪力钉时，最大活载系数和结构整体安全系数减小约一半，表明剪力连接件的刚度对组合梁斜拉桥的极限承载能力影响较大.由图14可知，不同剪力钉刚度对应的荷载位移曲线差别也较大，当布置大于0.5倍设计钢度的剪力钉时，在荷载较小的情况下，考虑粘结滑移和不考虑粘结滑移模型刚度相差不大，当荷载增大到一定程度并引起剪力件滑移后，结构的整体刚度会有所下降.但是当剪力钉的刚度小于0.5倍设计刚度时，考虑粘结滑移和不考虑粘结滑移模型的荷载位移曲线在一开始就相差比较大.

5 结论

本文结合某斜拉桥实际工程，对剪力钉刚度对组合梁斜拉桥受力性能的影响进行了参数分析，得到了以下结论:

(1)采用不同的剪力钉刚度时，界面滑移值沿桥梁纵向的分布规律基本一致，但数值差别较大，界面滑移值随着剪力钉刚度的减小而快速增大;

(2)剪力钉刚度对桥梁竖向挠度有重要影响，随着剪力钉刚度的降低，桥梁的竖向挠度逐渐增大.当界面无剪力钉时，其跨中挠度增幅达22.2%.

(3)考虑剪力钉的粘结滑移后，应变沿梁高的分布规律不再满足平截面假定，且偏离的程度随着剪力钉刚度的减小而增大.剪力钉刚度对中和轴位置的影响也十分明显，将导致出现钢梁受压，混凝土受拉的情况，组合梁桥设计时必须保证剪力钉有足够的刚度.

(4)剪力连接件的刚度对组合梁斜拉桥的极限承载能力影响较大，当混凝土板和钢梁界面无剪力钉时，结构的活载系数和整体安全系数减小约一半，当剪力件刚度小于设计刚度的0.5倍时，考虑粘结滑移和不考虑粘结滑移模型的荷载－位移曲线在一开始就相差比较大.

［1］ 蔺钊飞，刘玉擎.焊钉连接件峰值滑移及剪力—滑移本构关系［J］.同济大学学报:自然科学版，2014，42(7):1006-1010.LIN Z F，LIU Y Q.Peak slip and load-slip realationship of headed stud connectors［J］.J Tongji Univ:Nat Sci，2014，42(7):1006-1010.

［2］ OLLGAARD H G，SLUTTER R G，FISHER J D.Shear strength of stud connectors in lightweight and normal-weight concrete［J］.Engin J Amer Instit Steel Constr，1971，8(2):55-64.

［3］ 聂建国，陶慕轩，吴丽丽，等.钢-混凝土组合结构桥梁研究新进展［J］.土木工程学报，2012，45(6):110-122.NIE J G，TAO M X，WU L L，et al.Advances of research on steel-concrete composite bridges［J］.China Civil Engin J，2012，45(6):110-122.

［4］ DOGAN O，ROBERTS T M.Fatigue performance and stiffness variation of stud connectors in steel-concrete-steel sandwich systems［J］.J Constr Steel Res，2012，70(3):86-92.

［5］ CHEN X，KUNITOMO S，CHONG W，et al.Parametrical static analysis on group studs with typical push-out tests［J］.J Constr Steel Res，2012，72(5):84-96.

［6］ XUE D Y，LIU Y Q，YU Z，et al.Static behavior of multi-stud shear connectors for steel-concrete composite bridge［J］.J Constr Steel Res，2012，74(7):1-7.

［7］ XU X Q，LIU Y Q，HE J.Study on mechanical behavior of rubber-sleeved studs for steel and concrete composite structures［J］.Constr Build Mater，2014，53(2):533-546.

［8］ OLLGAARD J G，SLUTTER R G，FISHER J W.Shear strength of stud connectors in lightweight and normal-weight concrete［J］.AISC Engin J，1971，8(2):55-59.

［9］ BUTTRY K E.Behavior of stud shear connectors in lightweight and normal-weight concrete［R］.Kansas:Missouri State Highway Department and University of Missouri-Columbia，1965.

［10］ OEHLERS D J.The stiffness of stud shear connections in composite beams［J］.J Constr Steel Res，1986，6(4):273-284.

［11］ SHIM C S，LEE P G，YOON T Y.Static behavior of large stud shear connectors［J］.Engin Struct，2004，26(12):1853-1860.

［12］滕启杰.钢管混凝土拱桥的极限承载力研究［D］.大连:大连理工大学，2007.TENG Q J.Study on the ultimate bearing capacity of concrete filled steel tube arch bridge［D］.Dalian:Dalian University of Technology，2007.