基于游程编码的最大频繁项集挖掘算法

王茂华，郝云力，储小静

（阜阳师范学院，安徽 阜阳 236041）

1 概述

最大频繁项集的挖掘是数据挖掘领域的一个重要的研究方向[1].目前大部分的挖掘算法都是在经典的FP-MAX[2]、Mafia[3]等算法的基础上进行的改进，也有些学者提出了使用其他方法的最大频繁项集的挖掘算法.在文献[4]中，作者提出了一种基于链表运算的挖掘算法，该算法虽然抛弃了一部分的候选项，但是仍然会产生大量的冗余项.在文献[5]中，作者提出了一种基于布尔矩阵的最大频繁项集的挖掘算法，由于实际应用中数据量非常庞大，因此用布尔矩阵存储数据库会占用很大的存储空间.

针对以上存在的问题，文章提出了一种基于游程编码的最大频繁项集的挖掘算法RLCMAX.该算法不仅能减少事务数据库占用的存储空间，而且能有效提高算法的效率.

2 算法描述

2.1 数据库的游程编码表示

在数据库中，可以用1表示某项目被事物包含，0表示不被包含，因此可以用0-1序列来表示数据库.由于在0-1序列中只有0、1两个符号，而且总是交替出现，因此可以用游程编码来表示数据库.文章规定每个项目的游程序列必定从1-游程开始.如表1所示的数据库D.

表1 事物数据库D

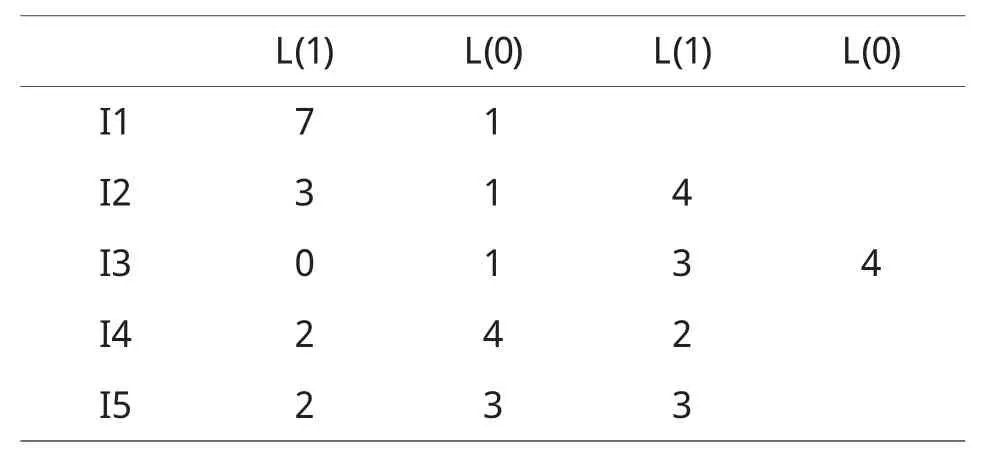
表2 游程序列表示的数据库

D中各项目可用表2中的游程序列表示.

由表2可以知道，项目的支持度必为1-游程的长度之和.

由于每个项目的游程个数是不确定的，所以可用单链表来表示游程序列.文章用链表数组来表示整个事物数据库.

2.2 算法的相关定义

定义1 链表数组TL是长度为n+1的指针数组，TL[i]指向项目Ii所对应的单链表，n为数据库中项目的个数.链表上每个结点包含2个域：data域和next域，其中data域为游程长度.

扫描一遍数据库，构造链表数组，最后删除支持度小于最小支持度的链表[6].如表1所示的数据库D可转换为图1所示的链表数组TL.

图1 链表数组TL

数据库中项目的支持度显然为链表中1-游程的data域之和.

定义2 链表集CL由若干个单链表组成，存储挖掘过程中产生的所有候选频繁项目集所对应的单链表.

定义3 非频繁项目集CBI存储不属于当前最大频繁项目集中的项目.

集合CB存储挖掘过程中产生的所有CBI.

定义4 频繁项目集CI存储当前的频繁项目集.

定义5 局部最大频繁项集 若集合FI是所有以Ij为起始项的频繁项集的集合，如果集合A∈FI,则对坌B∈FI且A≠B，有A不是B的子集，则称A为局部最大频繁项集.

2.3 游程编码的交运算

对任意两个链表C和F，从第一对结点开始求交，运算结果与结点是0-游程还是1-游程有关，基本思想描述如下：

1）若值大的结点Pmax为1-游程，转2），否则转3）.

2）若值小的结点Pmin为1-游程，转4），否则转5）.

3）若值小的结点Pmin为0-游程，转5），否则转4）.

4）若结果集合c1的尾元素Last(c1)是1-游程，则用结点Pmin的值与Last(c1)的和替换Last(c1)；否则将结点Pmin添加到集合c1中.

5）若结果集合c1的尾元素Last(c1)是0-游程，则将结点Pmin添加到集合c1中；否则用结点Pmin的值与Last(c1)的值替换Last(c1).

6）将结点Pmax和Pmin之差放入临时结点Lp中.

7）如果结点Lp的值为0，则Pmax、Pmin后移.否则，Pmax指向Lp，Pmin后移.

8）重复上述步骤，直到C,F都为空.

基于上述思路，游程编码的交运算用伪代码描述如下：

2.4 最大频繁项集的挖掘算法

算法采用回溯法搜索整个解空间的最大频繁项目集[4]，首先搜索出以I1为起始项的最大频繁项集,然后分别找出以Ij(j=2…n)为起始项的局部最大频繁项集，去掉其中的非最大频繁项集，最终可得所有的最大频繁项集.算法的具体思路如下：

1)搜索j层，链表集合CL的尾元素与Ij对应的链表L[j]相交，生成新链表.若新链表的1-游程之和不小于最小支持度min_sup时，将Ij添加到项目集合CI中，将新链表添加到CL中；否则，将Ij添加到项目集合CBI中.继续向j+1层搜索.

2)重复1），直到j>m，此时，CI必为局部最大频繁项集.若CI不是MFI中最大频繁项集的子集，则CI为最大频繁项集，将CI添加到MFI中，将CBI添加到集合CB中.转3）

3)返回j-1层，删除项目集合CI中项目Ij-1及其后面的所有项目，删除链表集合CL的尾元素.若存在Last(CB)的一个子集 B（对坌It∈B，有 t>j-1），有 CI∪B的项目支持度不小于最小支持度，且对坌In∈Last(CB)-B有CI∪In的项目支持度小于最小支持度(其中n>j-1),则所有以CI∪B为前缀的频繁项集必为局部最大频繁项集;将B中的项目添加到项目集合CI中，用CI∪B的链表替换Last(CL)，然后从Last(CB)中删除B中的项目，搜索下一层，转1）.否则如果CI为空,清空CB，搜索下一层，转1)；如果CI不为空且CB中存在2个以上的元素，删除CB的尾元素，返回上一层，重复3).

基于上述思路，算法用伪代码描述如下：

3 实例解释

以表1所示的数据库为例，最小支持度min_sup为2，求数据库的最大频繁项集，求解步骤如下：

1)初始化 CL={{8}},CI=覫,CB=覫;

2)进入第1层，选择项目I1，Last(CL)与I1对应的链表TL[1]相交得链表｛7,1｝，支持度为7，大于min_sup，则CI=CI∪{I1}={I1}，CL=CL∪{{7,1}}={{8},{7,1}}.

3)按照同样的步骤继续搜索，直到搜索完最底层即第5层，完成第一轮遍历，得到CI={I1,I2,I3},CL={{8},{7,1},{3,1,3,1},{0,1,2,5}},CB={{I4,I5}}.此CI即为最大频繁项集.

4)返回第5层，不选择I5.

5)返回第4层，不选择I4.

6)返回第3层，删除CI中的I3，删除CL的最后一项Last(CL)，逆序遍历 Last(CB)：

（1）选择Last(CB)中的项目I5，将Last(CL)与I5对应的链表TL[5]相交得链表{2,3,2,1}，支持度为4，大于min_sup.则，CI=CI∪{I5}={I1,I2,I5}，CL={{8},{7,1},{2,3,2,1}}，CB={{I4}}.

（2）选择Last(CB)中的项目I4，将Last(CL)与I4对应的链表TL[4]相交得链表{2,4,1,1}，支持度为3，大于min_sup.则 CI=CI∪{I4}={I1,I2,I5,I4}，CL={{8},{7,1},{2,3,2,1},{2,4,1,1}}，CB=覫.

7）进入第4层，由于I4已在CI中，不选.进入第5层，同样不选.则CI={I1,I2,I4,I5}必为最大频繁项集.

重复上述步骤，最终可以找到所有的最大频繁项集.

4 实验结果分析

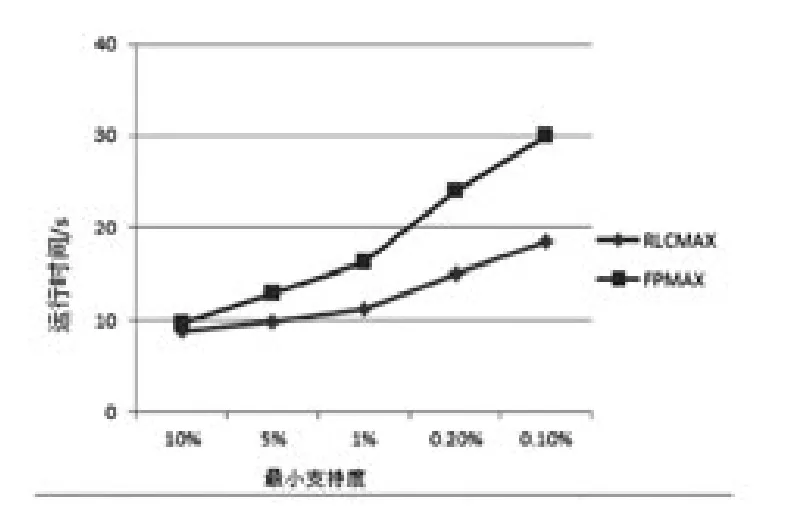
图2 性能比较

为验证算法的有效性，本文采用mushroom数据集进行验证，该数据集共有8124个事物，23个属性、127种取值，由于其第11个属性有2480个空值，在不影响实验结果的情况下删除该属性.算法检测的硬件平台是AMD 2.9GHZ CPU,2G内存，操作系统为WIN7，对比算法是FP-MAX算法.为保证数据正确，算法在每个比较中运行10次，计算均值作为结果.两种算法的实验结果如图2表示.从实验结果看，本文提出的RLCMAX算法性能要优于FPMAX算法.

5 结束语

本文提出的基于游程编码的最大频繁项集的挖掘算法，只需扫描数据库一次，将数据库转换为0-1游程编码表示的形式，并以链表数组存储转换后的数据库.通过对链表的交运算，直接得到局部最大频繁项集，剪枝力度非常大.当最小支持度发生变化时，本算法不需要重新扫描数据库和重新构造链表数组，就能很容易的挖掘最大频繁项集.

〔1〕Chen M S,Yu P S.Data Mining: An Overview from a Database Perspective [J]. IEEE Transactions on Knowledge and Data Engineering.1996,8(6):866–883.

〔2〕G Grahne and J Zhu.High Performance Mining of Maximal Fre -quent Itemsets [C].Proc.SIAM Workshop High Performance Data Mining: Pervasive and Data Stream Mining，May 2003．

〔3〕Burdick D,Calimlim M,Gehrke J. Mafia: A Maximal Fr -equentItemsetAlgorithm for Transactional Databases[A].In:Stuart Feldman ed,Proceeding of the 17 th International Conference on Data Engineering[C] . Washington:IEEE Computer Society Press,2001:443–452.

〔4〕刘应东，冷明伟，陈晓云.基于链表数组的最大频繁项集挖掘算法[J].计算机工程，2010，36(6):89–90.

〔5〕张世玲，李艳，王熙腾.一种基于布尔矩阵的最大频繁项集挖掘算法[J].计算机光盘与应用，2013（1）：192–193.

〔6〕胡双,邱金水,贺建峰.基于线性链表的 Apriori算法的改进[J].信息技术,2013（8）:48–50.