LED散热体冲压成形尺寸和形状的误差数学模型建立

郑天清，顾立志（华侨大学机电及自动化学院，福建厦门361021）



LED散热体冲压成形尺寸和形状的误差数学模型建立

郑天清，顾立志
（华侨大学机电及自动化学院，福建厦门361021）

摘要：基于误差反向传播算法，建立发光二极管（LED）散热体冲压成形尺寸和形状误差数学模型.阐述MATLAB神经网络工具箱求解误差数学模型的具体过程.针对某具体LED散热体产品，基于其相关的仿真数据与设计的MATLAB程序，求解出该LED散热体尺寸和形状误差数学模型.验证结果表明：实验的壁厚分布值与文中数学模型预测的壁厚分布值走势整体吻合，局部偏差不大；所建立的LED散热体冲压成形尺寸、形状误差数学模型具有一定的实用性.

关键词：误差反向传播；发光二极管；散热体；误差数学模型；壁厚

近年来，在全球节能意识高涨与相对较高的电价下，建筑、商业等应用领域持续引入发光二极管（light emitting diodes，LED）照明，使LED照明产业取得了突飞猛进的发展.随着LED照明产业的发展，LED灯具的设计与制造逐渐成为企业的研究热点［1－3］.散热体作为解决LED灯散热问题的关键部件，决定着LED灯的使用寿命，其设计与制造至关重要［4－5］.提高散热体的冲压成形精度逐渐也成为企业研究的重心之一.本文针对一LED散热体产品，基于误差反向传播算法，建立其尺寸和形状误差数学模型，以实现对其冲压成形误差的主动控制，提高其冲压成形精度和生产合格率，并节约生产成本.

1　模型的建立

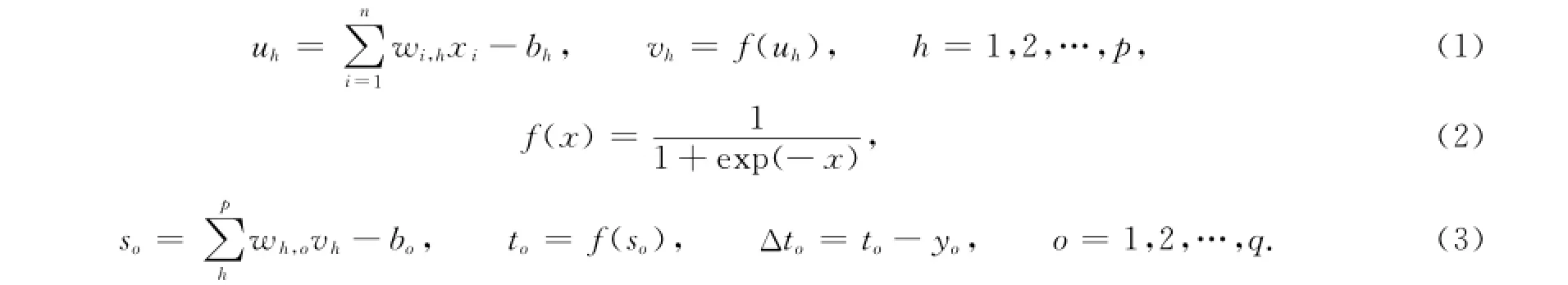
基于误差反向传播算法，LED散热体冲压成形尺寸和形状误差的数学模型［6－8］为式（1）～（3）中：x为影响因素值；n为误差数学模型中的输入层神经元个数，即影响因素个数；h为误差数学模型中的隐含层神经元；p为隐含层神经元个数；o为误差数学模型中的输出层神经元；q为输出层神经元个数；wi，h，wh，o分别为误差数学模型中不同的输入层与隐含层、隐含层与输出层的连接权值；bh，bo分别为误差数学模型中隐含层和输出层的各神经元阈值；f（.）为误差数学模型中激活函数；u＝（u1，u2，…，up），v＝（v1，v2，…，vp）分别为误差数学模型中隐含层输入向量和输出向量；s＝（s1，s2，…，sq），t＝（t1，t2，…，tq）分别为误差数学模型中输出层输入向量和输出向量，即为关键尺寸、形状特征的输出值；to为误差数学模型中输出层输出向量中的第o个输出，即为第o个关键尺寸、形状特征的t值；yo为第o个关键尺寸、形状特征的技术要求y值；Δto为第o个关键尺寸、形状特征的误差.

求解误差数学模型的关键在于求解误差数学模型中的待定系数wi，h，wh，o，bh，bo.利用BP神经网络，结合仿真得到的数据，可求解以上待定系数.

2　数学模型中待定系数的求解

2.1 基本原理

利用MATLAB的神经网络工具箱求解待定系数，其基本原理主要由以下9个步骤组成［9－10］.

步骤1 初始化神经网络.给wi，h，wh，o，bh和bo分别赋予一个区间（－1，1）内的随机数，设定误差

1q函数e＝2∑（do（k）－yo（k））2，设定计算精度值ε和最大学习次数M.

o＝1

步骤2 取第k个输入样本x（k）＝（x1（k），x2（k），…，xn（k））与其对应的期望输出d（k）＝（d1（k），d2（k），…，dq（k））.

步骤3 计算隐含层各神经元的输入uh（k）；基于激活函数，计算隐含层各神经元的输出vh（k），即激活函数（神经元）为

步骤4 基于神经网络的期望输出d（k）＝（d1（k），d2（k），…，dq（k））、神经网络的实际输出to（k），计算误差函数对输出层各神经元的偏导数δo（k），即

δo（k）＝（do（k）－to（k））to（k）（1－to（k））， o＝1，2，…，q.（7）

步骤5 基于隐含层到输出层连接权值wh，o（k）、输出层偏导数δo（k）、隐含层输出vh（k），误差函数对隐含层各神经元上的偏导数δh（k）进行相关计算，即

步骤6 基于输出层各神经元上的偏导数δo（k）和隐含层各神经元上输出vh（k），修正连接权值wh，o（k）和阀值bo（k），分别为式（9），（10）中：N表示调整前；N＋1表示调整后；η为学习率，在（0，1）之间取值.

步骤7 通过输入层各神经元上的输入xi（k）和隐含层各神经元的偏导数δh（k），修正连接权值wi，h（k）和阀值bh（k），即步骤8 计算全局误差E，即

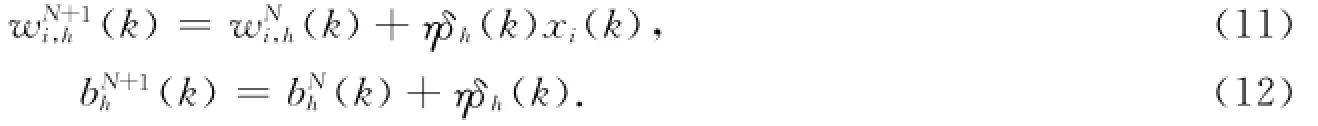
步骤9 判断神经网络误差是否满足要求.当E＜ε或学习次数大于设定最大次数M时，算法停止；否则，取下一个学习样本及相应期望输出，返回到步骤3，进入下一轮学习过程.

2.2 待定系数的求解

2.2.1 前处理 文中的LED散热体结构，如图1所示.由图1可知：LED散热体是由四道工序依次冲压而成的，分别为拉深、反拉深、冲孔与反拉深、落料与缩口.LED散热体最后的尺寸、形状误差是在每一道工序的尺寸、形状误差相互影响作用下形成的，相互间影响关系极其复杂，但基本的影响关系是一个误差累积的过程.LED散热体四道工序的仿真是通过导入上一道工序仿真结果文件中的dynain文件，完成坯料在DYNAFORM软件的导入，以实现上道工序的计算结果，传递到下道工序的模拟计算中，使应力应变场等计算结果相互继承［11－13］.在LED散

图1　LED散热体结构图（单位：mm）Fig.1　Structure figure of LED heat dissipation body（unit：mm）

图2　LED散热体成形零件的8节点位置Fig.2　8nodes location of the forming part of the LED heat dissipation

热体最后的仿真成形零件上均匀取8个节点，如图2所示.以四道工序中的5个工艺参数为输入数据，以基于DYNAFORM的LED散热体最后的仿真成形零件上8个节点的壁厚分布情况（t）、成形零件上8个节点主应变情况（ma）、成形零件上8个节点的次应变情况（mi）为输出数据.5个工艺参数如下：取第一至第四道凸模与板料、凹模与板料、压料板与板料、外支撑与板料、内支撑与板料的摩擦系数为同一值，1个工艺参数；级进模具的各工序冲压速度为同一值，1个工艺参数；第一道工序的压边力为1个工艺参数；第二道工序的压边力为1个工艺参数；第三道工序的压边力为1个工艺参数.8个节点的编号分别为：26025；26454；26716；26978；27146；26883；26618；26087.取16组L

ED散热体仿真数据作为训练样本（利用正交实验法进行训练，采用的正交实验表为L16（4），训练尺寸、形状误差数学模型，得到其中的权值与阀值，即可建立LED散热体的尺寸、形状误差数学模型.16组训练LED散热体尺寸、形状误差数学模型的输入数据，如表1所示；16组训练LED散热体尺寸、形状误差数学模型的输出数据，如表2所示.

表1　16组训练数学模型的输入数据（5×16）Tab.1　16groups of mathematics model training input data（5×16）

表2　16组训练数学模型的输出数据（24×16）Tab.2　16groups of mathematics model training output data（24×16）

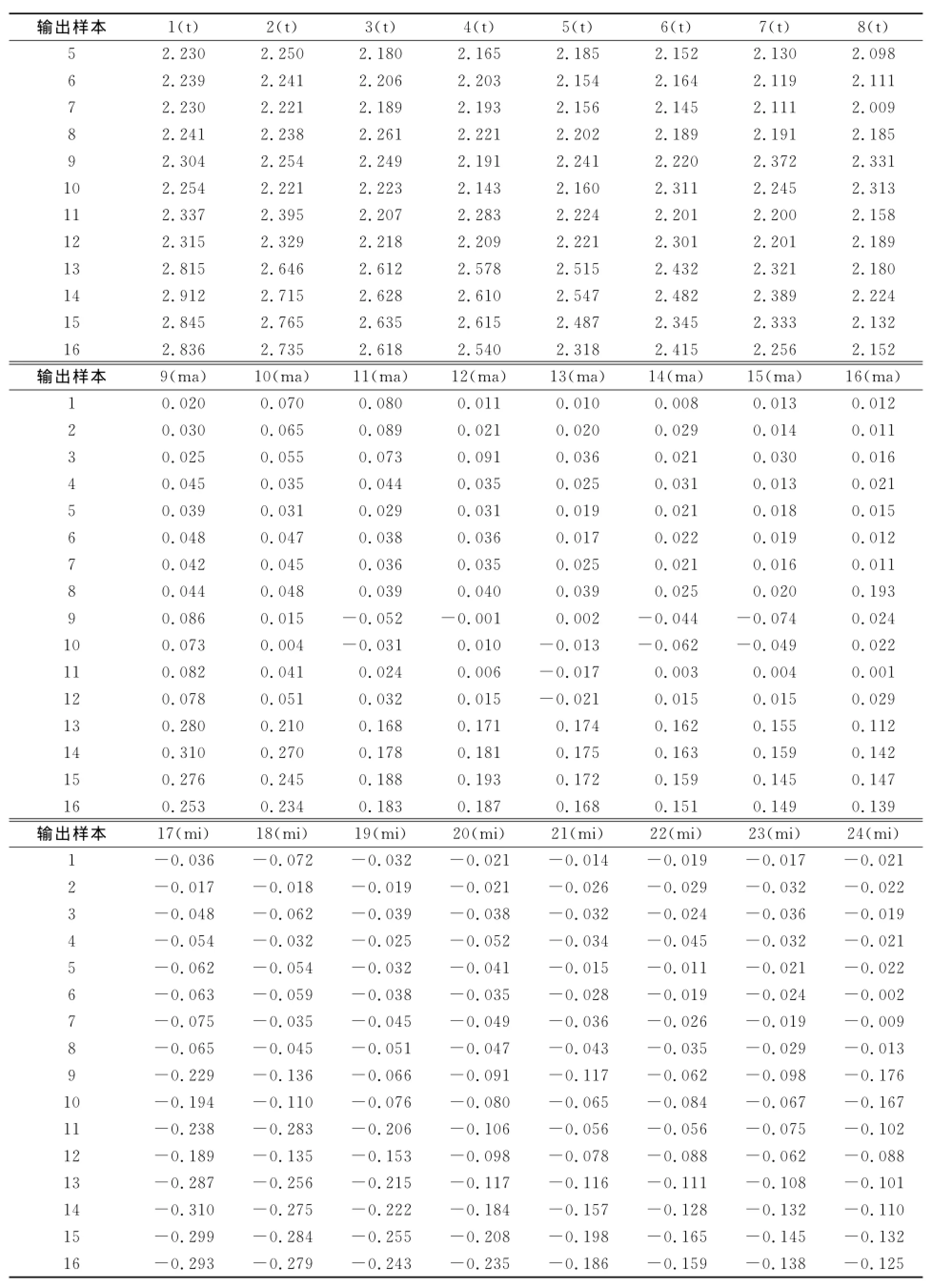
续表　Continue table

2.2.2 MATLAB求解待定系数的程序 求解待定系数的程序可表示为

2.2.3 权值与阀值 利用MATLAB的神经网络工具箱，经过108 596次数的迭代，大约45min的训练，得到LED散热体冲压成形尺寸、形状误差数学模型的权值与阀值.输入层到隐含层的权值是一个23×5阶的矩阵.隐含层到输出层的权值是一个24×23阶的矩阵.输入层到隐含层的阀值是一个23×1阶的矩阵.隐含层到输出层的阀值是一个24×1阶的矩阵.

图3　LED散热体成形零件Fig.3　Forming part of the LED heat dissipation body

3　实验验证

选择一组误差数学模型输入的工艺参数为0.1，60，100，80kN，500mm.s－1；相对应实验的工艺参数为0.1，60，100，80kN，500 mm.s－1.其实验冲压出的零件，如图3所示.实验壁厚分布值与LED散热体尺寸、形状误差数学模型预测壁厚分布值对比，如图4所示.图4中：d为壁厚分布值.由图4可知：实验壁厚分布值与文中数学模型预测壁厚分布值整体吻合，局部偏差不大，证明了文中所建数学模型具有较强的预测能力和较强的实用性.

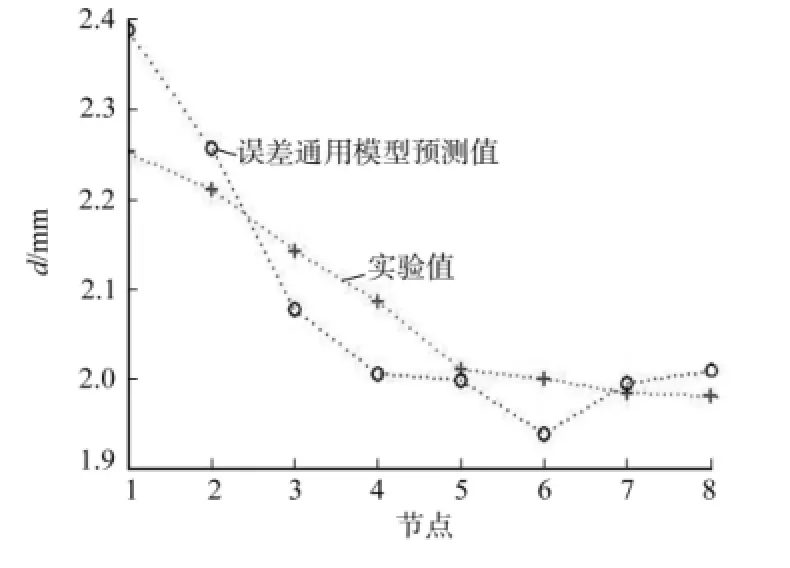
图4　模型预测与实验的壁厚分布值对比Fig.4　Wall thickness comparison between the model predicted value and experimental value

4　结论

基于误差反向传播算法，建立LED散热体尺寸和形状误差数学模型.说明了待定系数wi，h，wh，o，bh，bo是建立该数学模型的关键问题，阐述了MATLAB神经网络工具箱求解待定系数wi，h，wh，o，bh，bo的基本原理.

针对某LED散热体产品，其冲压成形由四道工序完成，通过提取此LED散热体四道工序的仿真工艺参数为输入数据，基于DYNAFORM仿真成形零件上的8个节点的壁厚分布情况（t）、主应变情况（ma）、次应变情况（mi）为输出数据；此外，基于MATLAB神经网络工具箱、输入与输出数据，设计相应的MATLAB程序，求出此数学模型的待定系数，即得到了该LED散热体尺寸、形状误差数学模型.

通过实验验证，对比了实验壁厚分布值与文中数学模型壁厚预测分布值.结果表明：分布值整体吻合，局部偏差不大，证明了该LED散热体误差数学模型具有较强的实用性.

参考文献：

［1］佟鑫.LED灯具散热器的结构研究与优化设计［D］.长春：吉林大学，2013：1－6.

［2］李琳红.大功率LED模组及工矿灯散热分析［D］.重庆：重庆大学，2012：1－8.

［3］张雪粉.大功率LED散热研究及散热器设计［D］.天津：天津大学.2007：1－9.

［4］张驰，吕文婷，徐沛娟，等.大功率LED照明灯散热装置研究［J］.新技术新工艺，2011（3）：1－3.

［5］杨广华，李玉兰，王彩凤，等.基于LED照明灯具的散热片设计与分析［J］.电子与封装，2010，81（1）：39－42.

［6］李小燕.灰色神经网络预测模型的优化研究［D］.武汉：武汉理工大学，2009：10－56.

［7］韩飞，莫健华，龚攀.基于遗传神经网络的数字化渐进成形回弹预测［J］.华中科技大学学报，2008，36（1）：121－124.

［8］陈涛，龚正虎，胡宁，等.基于改进BP算法的网络态势预测模型［J］.中国电子商情：通信市场，2009（2）：93－99.

［9］党建武.神经网络技术及应用［M］.北京：中国铁道出版社，2000：25－32.

［10］李友坤.BP神经网络的研究分析及改进应用［D］.淮南：安徽理工大学，2012：20－55.

［11］安治国.径向基函数模型在板料成形工艺多目标优化设计中的应用［D］.重庆：重庆大学，2009：81－108.

［12］张彬，李东升，周贤宾.基于人工神经网络的拉形回弹预测技术研究［J］.塑性工程学报，2003，10（2）：28－31.

［13］魏光明.多工位级进冲压工艺分析及成形全工序数值模拟［D］.广州：华南理工大学，2012：35－40.

（责任编辑：黄晓楠 英文审校：杨建红）

Establishment of the Mathematical Model of Stamping Size and Shape Error for LED Heat Dissipation Body

ZHENG Tian－qing，GU Li－zhi
（College of Mechanical Engineering and Automation，Huaqiao University，Xiamen 361021，China）

Abstract：Based on error back propagation algorithm，the mathematical model of stamping size and shape error for light emitting diodes（LED）heat dissipation body was established.Explain the specific process to solve the error mathematics model using MATLAB neural network toolbox.Based on a product of LED heat dissipation body，used the related simulation data and the designed MATLAB program to solve the mathematical model of stamping size and shape error for LED heat dissipation body.Verification results showed that the overall value was matched and the local deviation was little for the comparison between the experimental value of the wall thickness distribution and the mathematics model predicted value of that in this paper，the established mathematical model of stamping dimension－error and shape－error for LED heat dissipation body has fine practicality.

Keywords：error back propagation；light emitting diodes；heat dissipation body；error mathematical model；wall thickness

通信作者：顾立志（1956－），男，教授，博士，主要从事数字化设计制造的研究.E－mail：gulizhi888＠163.com.

中图分类号：TH 128；TH 161

文献标志码：A

文章编号：1000－5013（2015）04－0371－06

doi：10.11830/ISSN.1000－5013.2015.04.0371

收稿日期：2014－12－29

基金项目：福建省科技计划项目（2014I01010233）