一类调和映照的系数估计

阙玉琴，陈行堤（华侨大学数学科学学院，福建泉州362021）



一类调和映照的系数估计

阙玉琴，陈行堤
（华侨大学数学科学学院，福建泉州362021）

摘要：在单叶调和映照的系数猜想的基础上，获得单叶调和映照在第二复伸张满足标准化条件下的系数估计，结果渐进于单叶函数的系数估计，建立了两个猜想的联系，并获得此类映照的增长和覆盖定理.

关键词：单叶调和映照；稳定调和映照；系数估计；增长定理

1　预备知识

若f（z）为定义在单位圆盘D＝｛｜z｜＜1｝上的调和映照，则存在D上的两个解析函数h（z）和g（z），使得f（z）＝h（z）＋g（z），且称h（z）和g（z）为f的解析元和反解析元［1－11］.由Lewy［6］定理知，调和映照f在单位圆上局部单叶当且仅当

若Jf＞0，则f为单位圆盘上的保向调和映照，其第2复伸张为ω（z）＝g′（z）/h′（z），且在单位圆内满足｜ω（z）｜＜1.SH表示单位圆盘上的单叶保向调和映照且具有展式，即的全体.记S0H＝｛f∈SH∶fz（0）＝0｝.

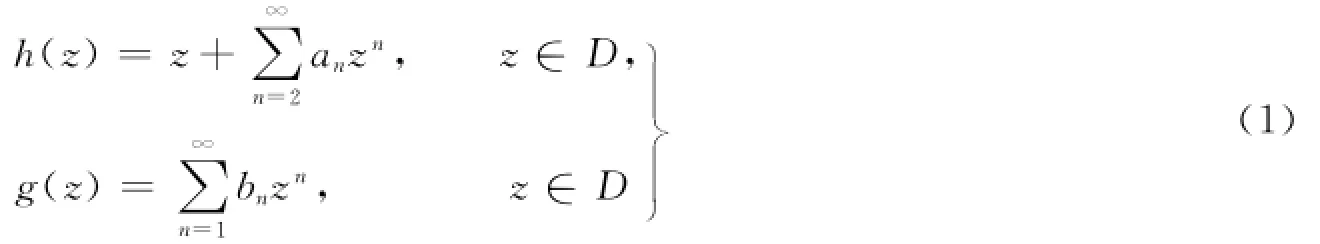
经典的单叶解析函数类，即

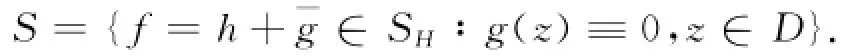
1985年，de Branges［4］证明了Bieberbach猜想，当n≥2时，｜an｜≤n.1984年，Clunie等［1］提出了规范化单叶调和映照的系数猜想A.

猜想A 如果f＝h＋g珚∈S0H，且h和g的表达式为（1），那么不等式

对所有的n≥2成立.当f（z）为调和Koebe函数，即时，等号成立.

这个猜想在S0H一些子类是成立的，如凸、星象、近于凸、典型实和沿一个方向凸的单叶调和映照类［1，10－11］.记

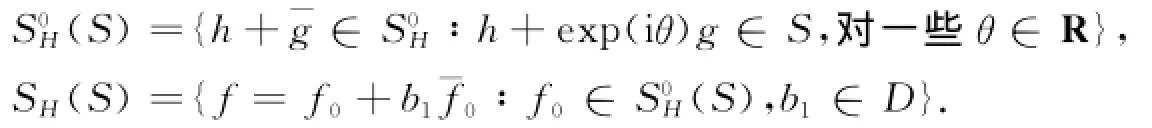
2014年，Ponnusamy等［8］证明了猜想A在类H0H（S）也是正确的，即定理A.

定理A 设f＝h＋珚g∈S0H（S），式（1）为h和g的表达式，则对所有的n≥2，式（2）成立.这是S0H（S）类系数的精确上界，当f为调和Koebe函数K（z）时，等号成立.

2013年，Hernández等［7］提出了稳定性理论.如果调和映照f＝h＋g珚单叶（凸）且对于所有的θ有fθ＝h＋exp（iθ）g珚单叶，则称f是稳定单叶（凸）；而且还证明了若调和映照f＝h＋珚g稳定单叶当且仅当解析函数F＝h＋g稳定单叶.不是所有的调和映照都是稳定单叶的，比如调和Koebe函数只在θ＝π时成立.2014年，Ponnusamy［8］提出了一个猜想：对于每一个，一定存在一个θ使得h＋exp（iθ）g∈S.

文中继续研究S0H（S）类调和映照，利用第2复伸张的标准化条件，得到渐进于经典的单叶解析函数类S的系数估计.

2　主要定理及证明

定理1 假设单位圆盘上的保向调和映照f＝h＋珚g∈S0H（S），h和g的表达式满足式（1），其第2复伸张为ω（z）满足ω（0）＝0，ω′（0）＝0，ω″（0）＝0，…，ω（m－1）（0）＝0，ω（m）（0）≠0.

当n≤m时，有

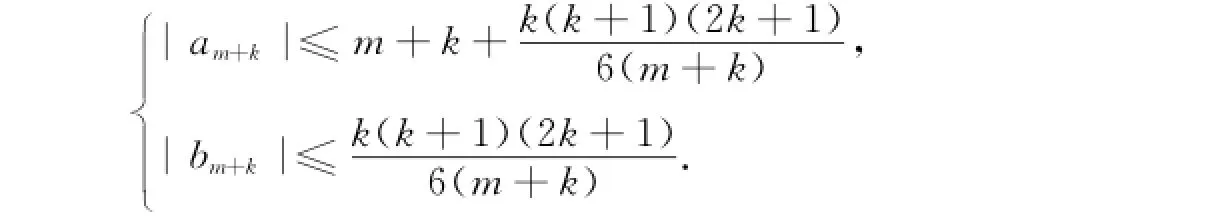
当n＝m＋k，k＝1，2，3，…时，有特别地，当m→∞时，｜an｜≤n；当m＝1时，｜an｜≤（n＋1）（2n＋1）/6，｜bn｜≤（n－1）（2n－1）/6.证明 因为f＝h＋g珚∈S0H（S），所以存在一个θ，使得

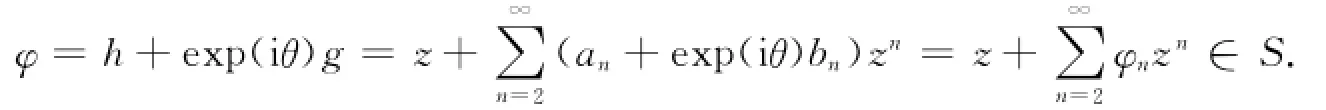
由de Branges定理，当n≥2时，｜φn｜≤n.因为f为保向的调和映照，所以ω（0）＝0，且对于所有的z∈D，有

而且有所以有

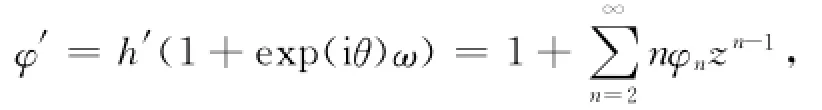
因为ω（z）满足ω（0）＝0，ω′（0）＝0，ω″（0）＝0，…，ωm－1（0）＝0，ωm（0）≠0，所以有

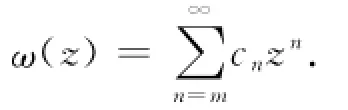
又由于

所以，可令

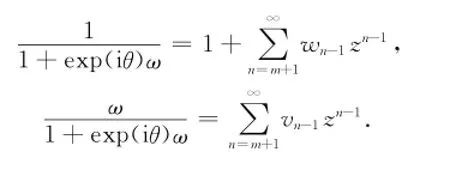
因为｜ω（z）｜＜1，由从属原理根据Rogosinski定理［9］，对所有的n，有

｜wn－1｜≤1， ｜vn－1｜≤1.

因此有

当n＝m＋1时，有

∞

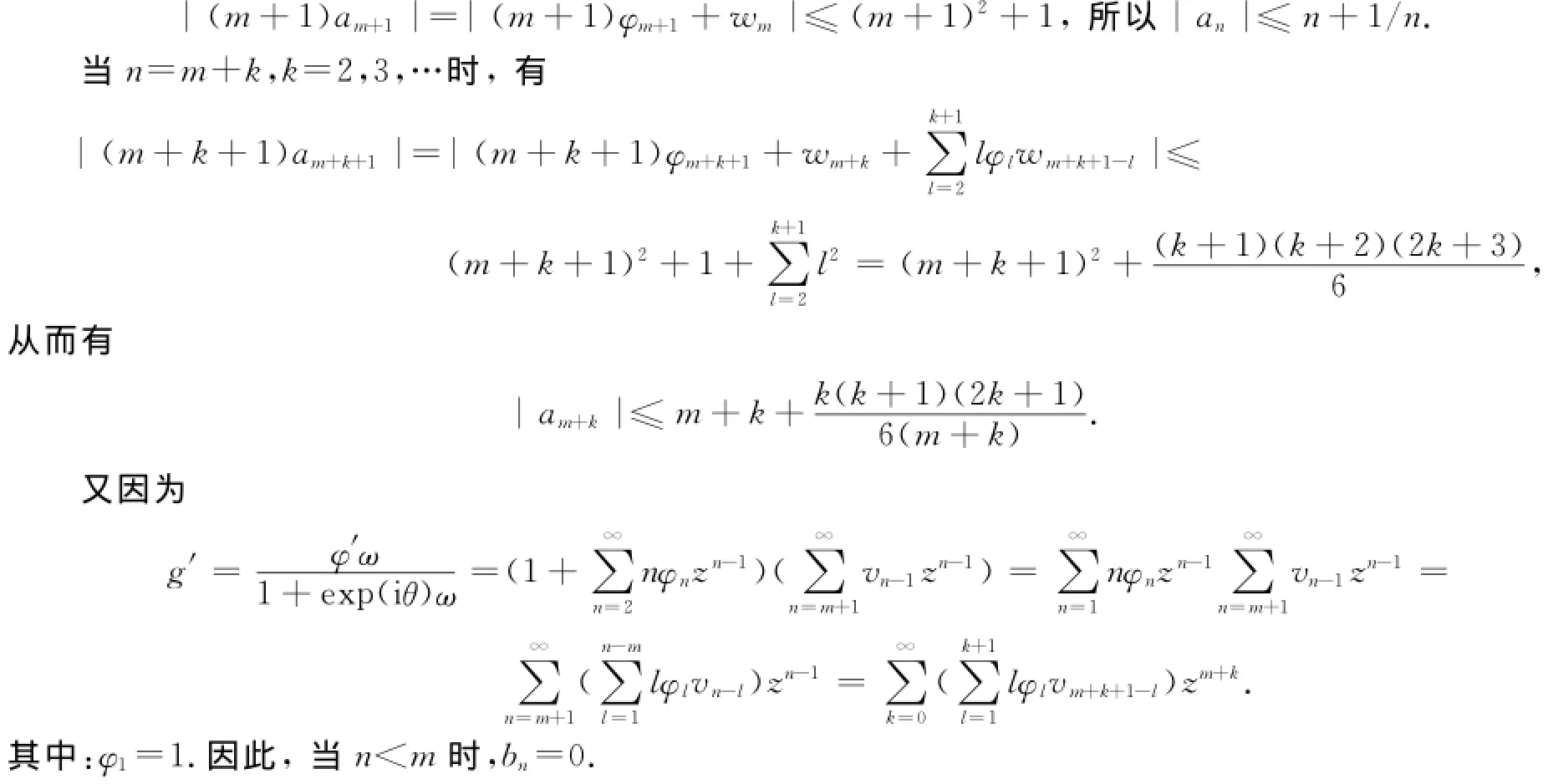
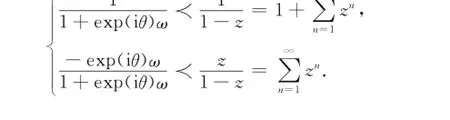
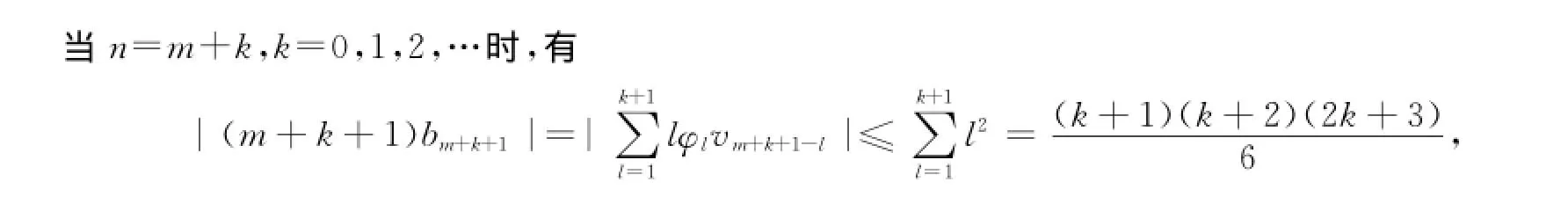
所以

特别地，当m→∞时，｜am＋k｜≤m＋k，即｜an｜≤n，｜bn｜＝0，其为解析函数类的系数估计；当m＝1，｜an｜≤（n＋1）（2n＋1）/6，｜bn｜≤（n－1）（2n－1）/6，其为Ponnusamy的S0H（S）类的系数估计.

由于解析函数S类的子类凸函数的系数估计为当n≥2时系数的模小于等于1，所以类似定理1的证明得到.

推论1 假设f＝h＋珚g∈S0H（C），其中，h和g满足式（1）且第2复伸张ω（z）满足式（4），则当n≤m时，有

当n＝m＋k，k＝1，2，3，…时，有

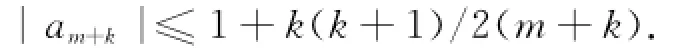
特别地，当m→∞时，｜an｜≤1；当m＝1时，｜an｜≤（n＋1）/2.

推论2 假设f＝h＋珚g∈SH（S），其中h和g满足式（1），则当n＜m时，有

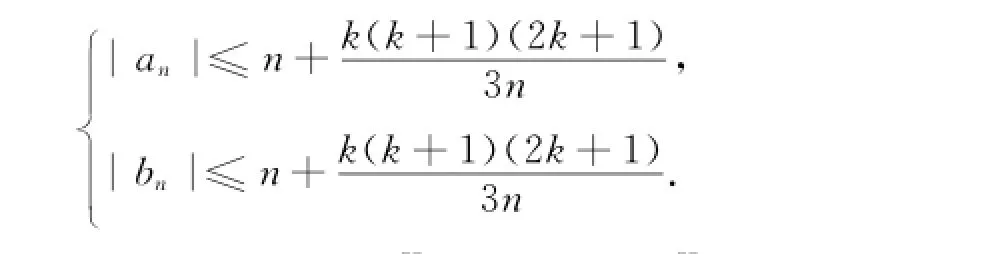
证明 设f0＝h0＋g珚0∈S0H（S），其中且其第2复伸张ω0（z）满足则

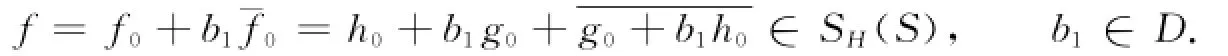
由定理1，当n＜m时，有

｜a0，n｜≤n， ｜b0，n｜＝0.

当n＝m＋k，k＝0，1，2，…时，有

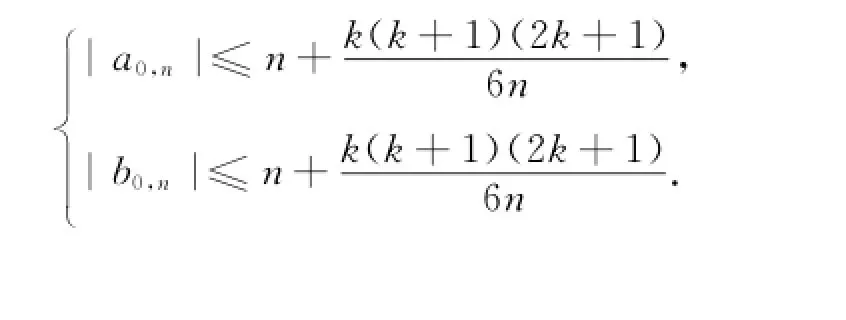
所以，当n＜m时，有｛｜an｜＝｜a0，n＋b1b0，n｜≤｜a0，n｜＋｜b0，n｜≤n，｜bn｜＝｜b0，n＋b1a0，n｜≤｜b0，n｜＋｜a0，n｜≤n.，2，…时，有

当n＝m＋k，k＝0，1（）（）

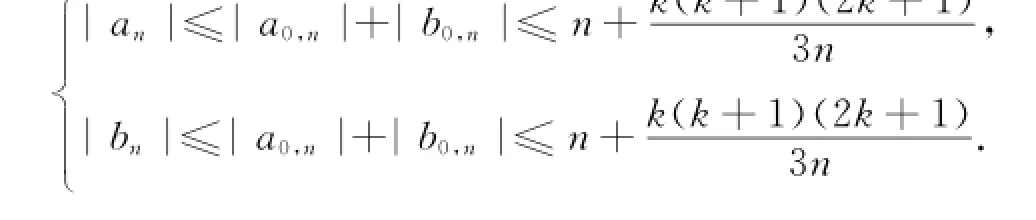
3　结果的运用

SH（S）类有下列的性质：若，则函数为

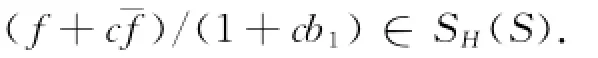
其中：c∈D，此性质称为仿射不变.类似地，若f∈SH（S），则函数为

此性质称为线性不变.定理B为SH类调和函数的增长和覆盖定理［3］.

定理B 假设α是所有函数f∈SH类第二项系数｜a2｜的上确界，则对于每个函数f∈S0H满足

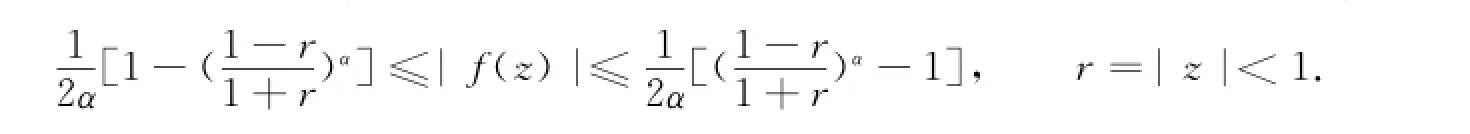
特别地，每个函数f∈S0H包含一个1/2α圆.

定理1证明了第2复伸张满足式（4）的S0H（S）类的精确系数估计，作为定理1的运用，可以证明第2复伸张满足式（4）的条件下S0H（S）类的精确系数估计.利用定理B，给出一个S0H（S）类更优的增长和覆盖定理.

定理2 对每一个复伸张满足式（4）的f∈S0H（S），当m＞1时，满足下面的不等式，即

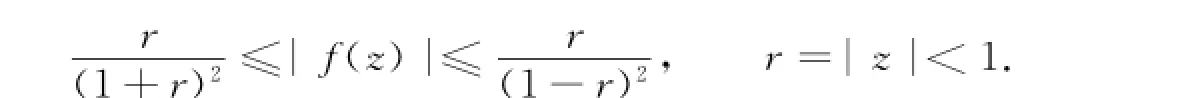
特别地，此类映照包含了一个1/4圆.

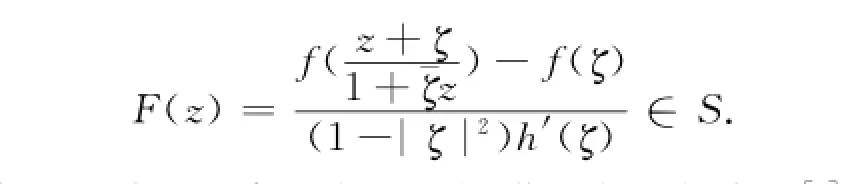
参考文献：

［1］CLUNIE J G，SHEIL－SMALL T.Harmonic univalent functions［J］.Ann Acad Sci Fenn Ser A L，1984，9（1）：3－25.

［2］DUREN P.Univalent functions［M］.New York：Springer－Verlag，1983：17－21.

［3］DUREN P.Harmonic mappings in the plane［M］.Cambridge：Cambridge University Press，2004：86－110

［4］de BRANGES L.A proof of the Bieberbach conjecture［J］.Acta Math，1985，154（1/2）：137－152.

［5］GREINER P.Geometric properties of harmonic shears［J］.Comput Methods Funct Theory，2004，4（1）：77－96.

［6］LEWY H.On the non－vanishing of the Jacobian in certain one－to－one mappings［J］.Bull Amer Math Soc，1936，42 （1）：689－692.

［8］PONNUSAMY S，KALIRAJ A S.On the coefficient conjecture of clunie and sheil－small on univalent harmonic mappings［DB/OL］［2014－03－22］.http：∥arxiv.org/abs/1403.5619.

［9］ROGOSINSKI W.On the coefficients of subordinate functions［J］.Proc London Math Soc，1990，42（1）：237－248.

［10］SHEIL－SMALL T.Constants for planar harmonic mappings［J］.J London Math Soc，1990，42（1）：237－248.

［11］WANG Xiao－tian，LIANG Xiang－qian，ZHANG Yu－qin.Precise coefficient estimates for close－to－convex harmonic univalent mappings［J］.J Math Anal Appl，2001，263（2）：501－509.

（责任编辑：陈志贤 英文审校：黄心中）

On the Coefficient Estimates for One Subclass of Harmonic Mappings

QUE Yu－qin，CHEN Xing－di
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

Abstract：We study the coefficient estimates of a subclass of harmonic mappings，which second complex dilatations satisfy some normal condition.The result is asymptotic to the estimates of univalent analytic functions，the relationship of the coefficient conjecture of these two class mappings is established.We also obtain the growth and covering theorem for this class of mappings.

Keywords：harmonic mapping；stable harmonic mapping；coefficient estimate；distortion theorem

通信作者：陈行堤（1976－），男，副教授，博士，主要从事函数论的研究.E－mail：chxtt＠hqu.edu.cn.

中图分类号：O 174.55

文献标志码：A

文章编号：1000－5013（2015）04－0484－05

doi：10.11830/ISSN.1000－5013.2015.04.0484

收稿日期：2014－10－27

基金项目：国家自然科学基金资助项目（11471128）；福建省自然科学基金计划资助项目（2014J01013）；华侨大学中青年教师科研提升资助计划（ZQN－YX110）