某些近于凸调和函数的解析性质和系数估计

黄赟，黄心中（华侨大学数学科学学院，福建泉州362021）



某些近于凸调和函数的解析性质和系数估计

黄赟，黄心中
（华侨大学数学科学学院，福建泉州362021）

摘要：研究单位圆盘D上某些具有稳定近于凸的调和函数f（z）＝h（z）＋g（z）解析部分h（z）满足Re｛1＋时的解析表示和系数估计表达式.对其复伸张w（z）为一次多项式时，给出了f（z）的稳定近于凸的判别条件，并且推广了Bshouty和Nagpal等的结果.特别地，当时，估计了f＝h＋g珚在单位圆盘上的稳定近于凸半径.

关键词：调和函数；稳定近于凸；系数估计；单叶半径

1　预备知识

Mocanu［2］定义了一个函数类：对所有z∈D满足不等式同时，提出如下猜想：M中的函数是单叶的.Bshouty等［1］利用解析函数近于凸的两个引理证明了以上猜想，并在文章中给出更强的结果：对于M中的调和函数不仅是单叶的，而且是近于凸的.

Nagpal等［3］引入具有正实部的函数，并用对比系数对M中的调和函数做出精确的系数估计：，等号在达到.

Bshouty等［4］对近于凸单叶调和函数的范围进行推广，利用圆盘的辐角改变量得到更为一般化的定理，并对满足条件的函数类的伸张偏差范围做出估计.他们证明了以下两个定理.

定理A 若h是单位开圆盘D上的解析凸函数，则调和函数f＝h＋g珚是近于凸的，其中

Bshouty等［5］提出了如下问题：令f＝h＋g珚是D上的调和函数如果，满足调和函数f的单叶性如何.

对于具有稳定近于凸调和函数的研究，今年来有不少进展［6－8］.本文利用解析函数近于凸的两个引理，将调和函数的单叶性证明推广到更为一般的函数形式，并对这类函数的系数做出估计，得到一些精确的结果.

2　主要结果及证明

令Q（D）＝｛h（z），h（z）为D上的解析函数，且满足.证明h（z）具有以下的表示定理.

定理1 h（z）∈Q（D）的充分必要条件是存在正实部函数p（z）＝1＋c1z＋c2z2＋…，使得其中：1≤k＜3/2.证明 设函数h（z），满足h（0）＝0，h′（0）＝1，且令则p（z）是正实部函数，且p（0）＝1，有两边同时积分得令k＝1－c，1≤k＜3/2，两边同时积分得反之，设存在正实部函数p（z），使得h（z）写成如下形式，即其中：1≤k＜3/2.则有

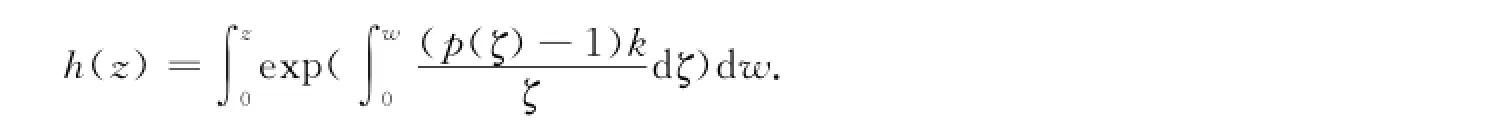
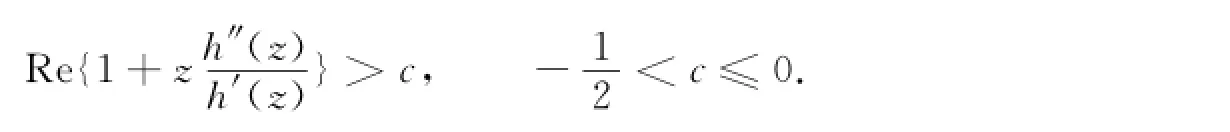
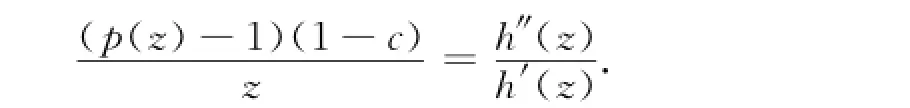
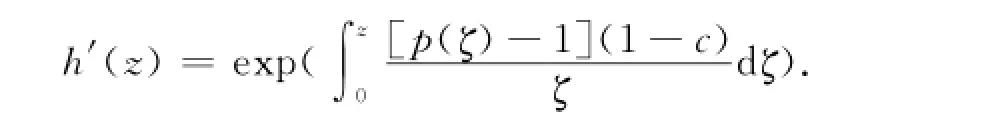
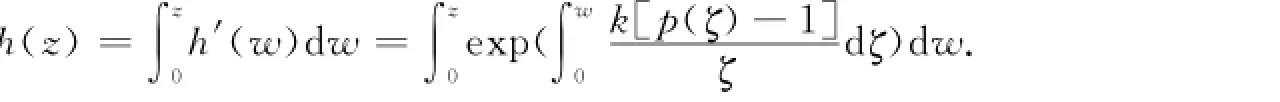
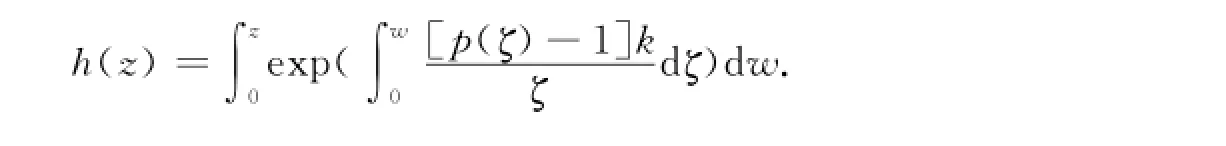
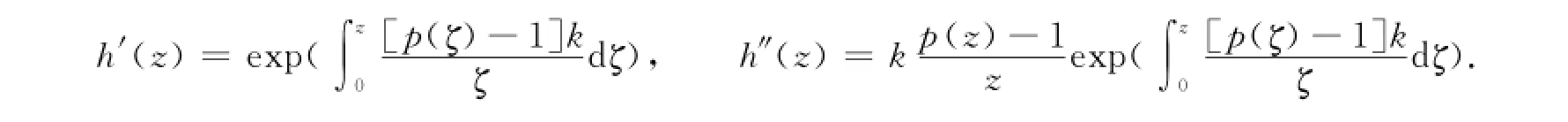
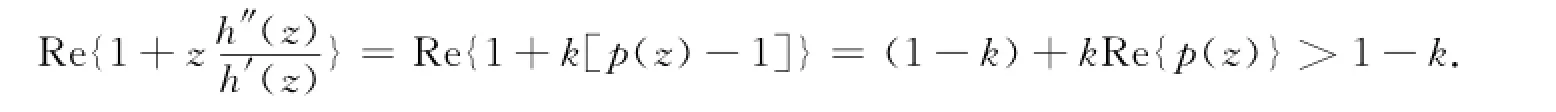
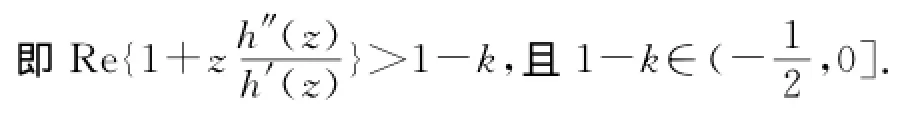
故 Bshouty等［1］已经证得：条件为）的单叶性.

为此，引入下面引理1，2.

引理1［9］解析函数h定义在D上，h是近于凸的充分必要条件为h′（z）≠0，且满足其中

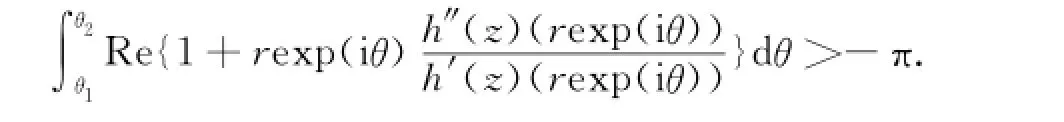
引理2［10］若调和函数满足

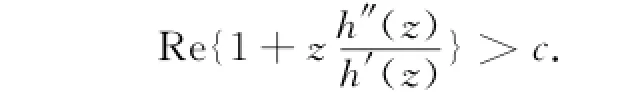
证明 考虑解析函数F（z）＝h（z）－λg（z），其中，｜λ｜＝1，则

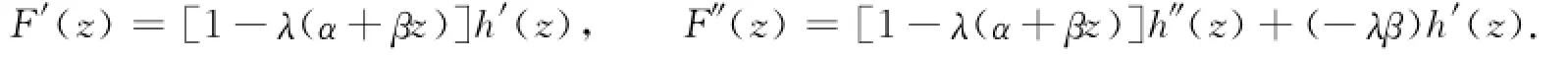
显然，在单位圆盘D上F′（z）≠0，则

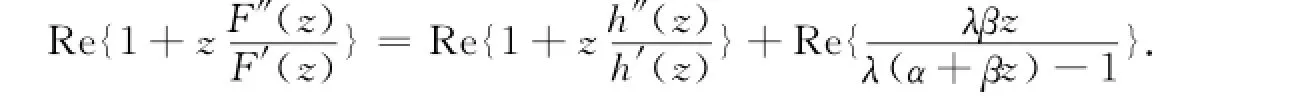
因此，F（z）＝h（z）－λg（z）是近于凸的.由于g′（0）＝αh′（0），根据引理2，f（z）＝h（z）＋g（z）是稳定近于凸调和函数.

对于这一类函数，可以通过下面的定理对其系数进行估计.

定理3 设f（z）＝h（z）＋g（z）是定义在单位圆盘D上的调和函数，f，g可以表示为h（z）＝z＋

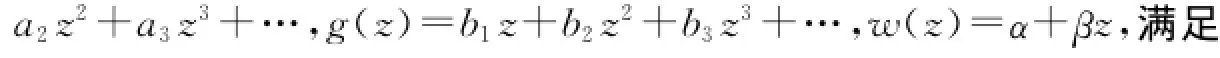
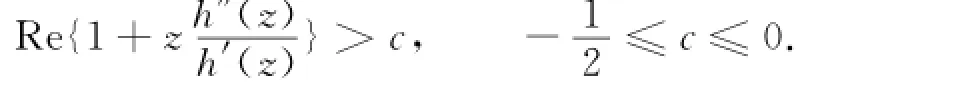
其中：z∈D，则有系数估计

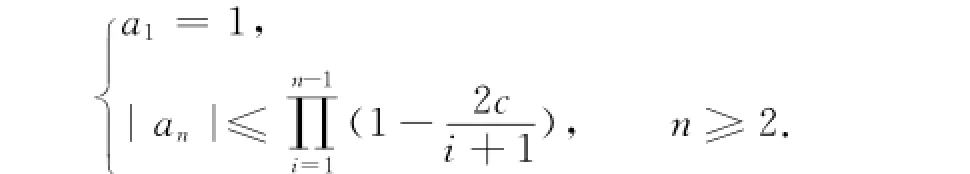
也可表示为

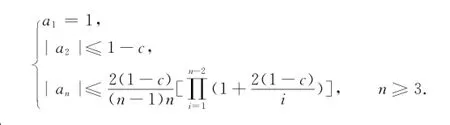
bn的系数估计为

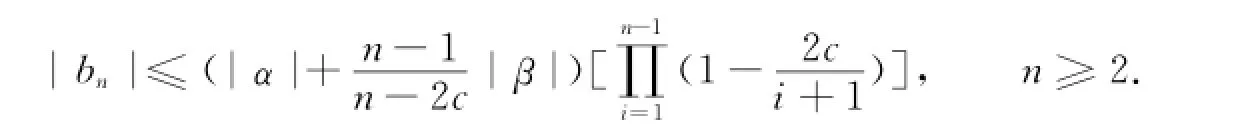
由于h（z）在单位圆盘上局部单叶，函数p（z）＝1＋c1z＋c2z2＋…是D上具有正实部的解析函数.因此，｜cn｜≤2对于n＝1，2，…都成立.根据［p（z）－1］（1－c）h′（z）＝zh″（z），对比zn的系数得到（n＋

n

1）nan＋1＝（1－c）∑kakcn＋1－k，n＝1，2，….则有

k＝1下面证明上述系数估计有另外的表达形式.当n≥3时，有n－2

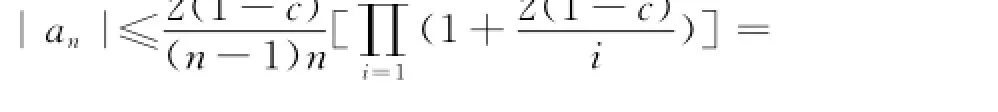
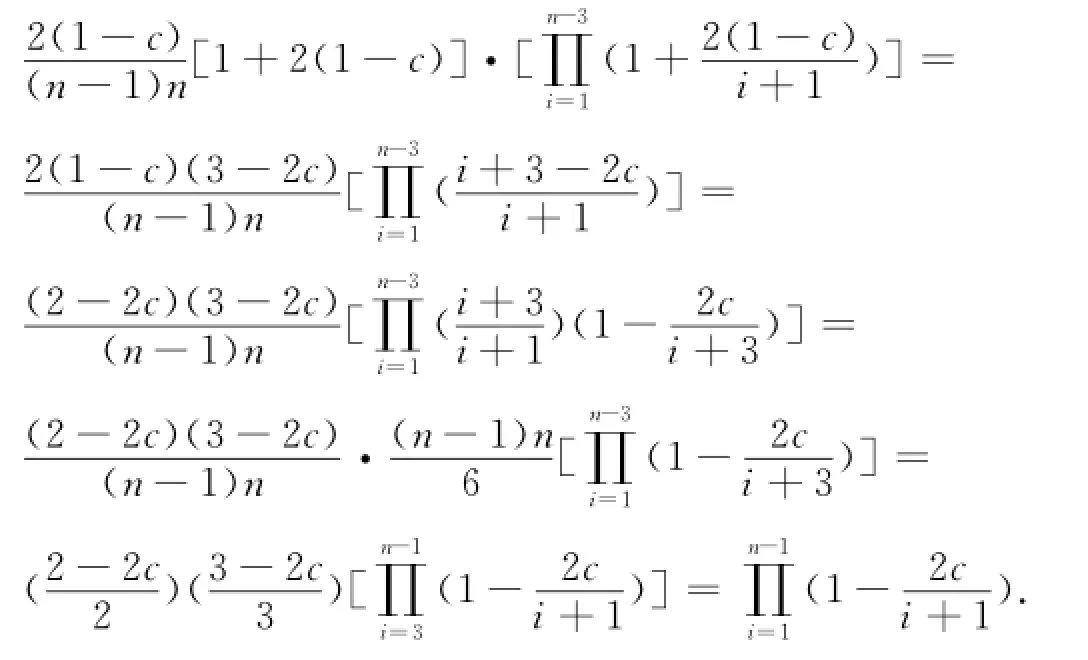
当n＝2时，｜a2｜≤1－c也满足上式，即可得到系数估计的另一种形式

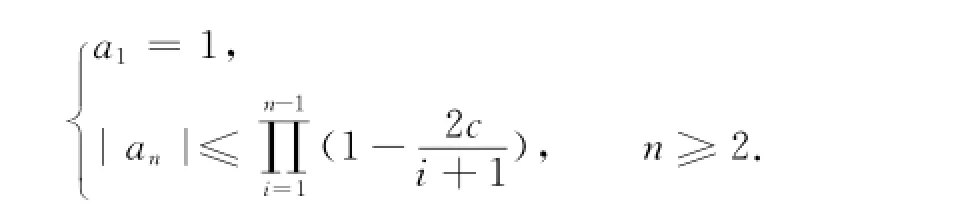
接下来考虑｜bn｜的范围，根据g′（z）＝（α＋βz）h′（z），对比zn的系数关系，有（n＋1）bn＋1＝α（n＋1）an＋1＋βnan.则有

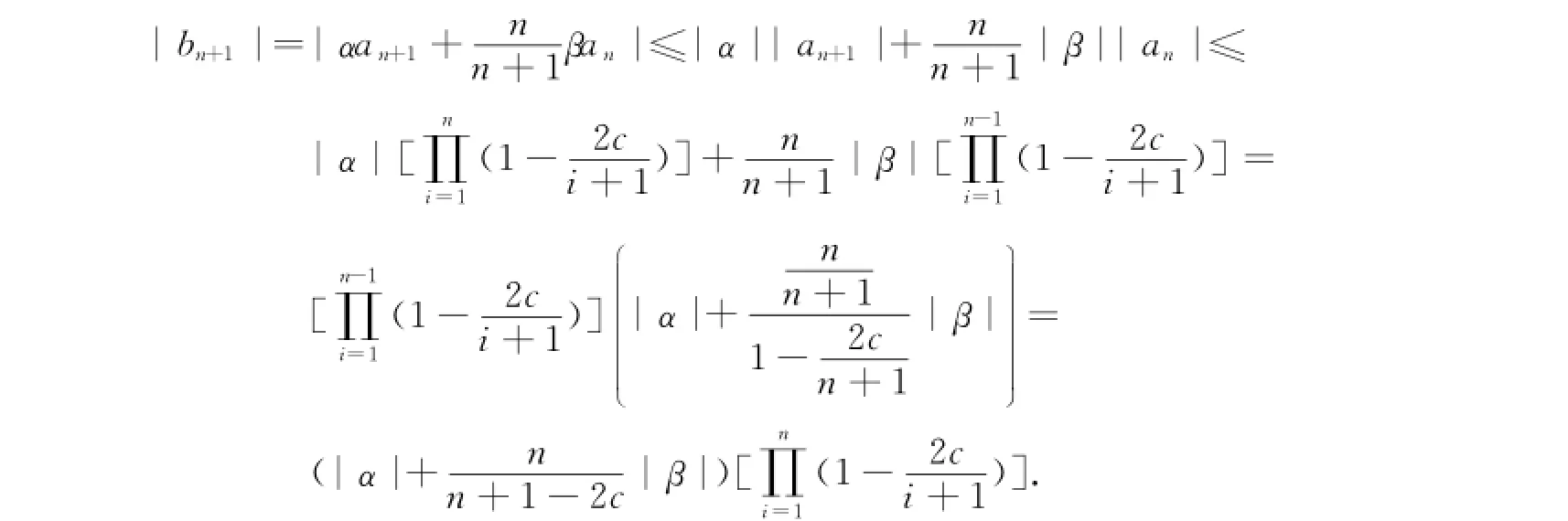
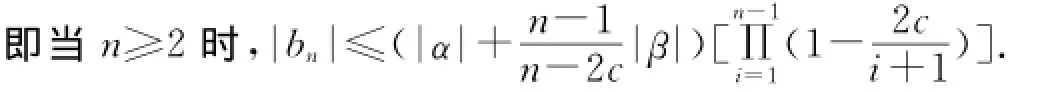
定理3证毕.

以上估计是精确的.

Bshouty等［5］提出一系列的问题和猜想.其中，问题3.14提出当满足条件的情况下的最大叶数为多少.定理4估计了当w（z）＝z2时，f的稳定近于凸半径，部分回答了这一问题.

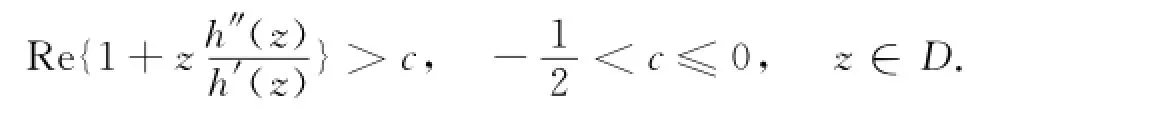
定理4 设f（z）＝h（z）＋g（z）是定义在单位圆盘D上的调和函数，h′（0）≠0，满足当w（z）＝z2时，调和函数f（z）的稳定近于凸半径r≥槡（1＋2c）/（5＋2c）.证明 考虑解析函数F（z）＝h（z）－λg（z），其中，｜λ｜＝1，那么

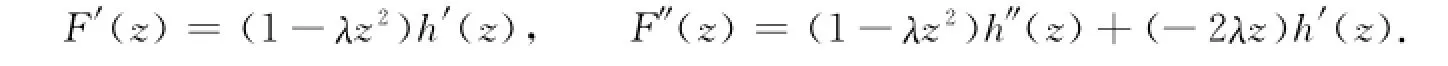
显然，在D上F′（z）≠0，故其中：θ1＜θ2＜θ1＋2π.

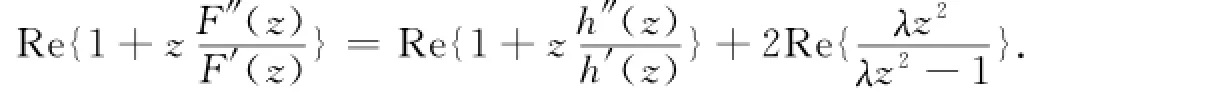
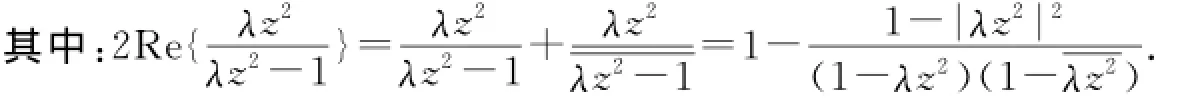
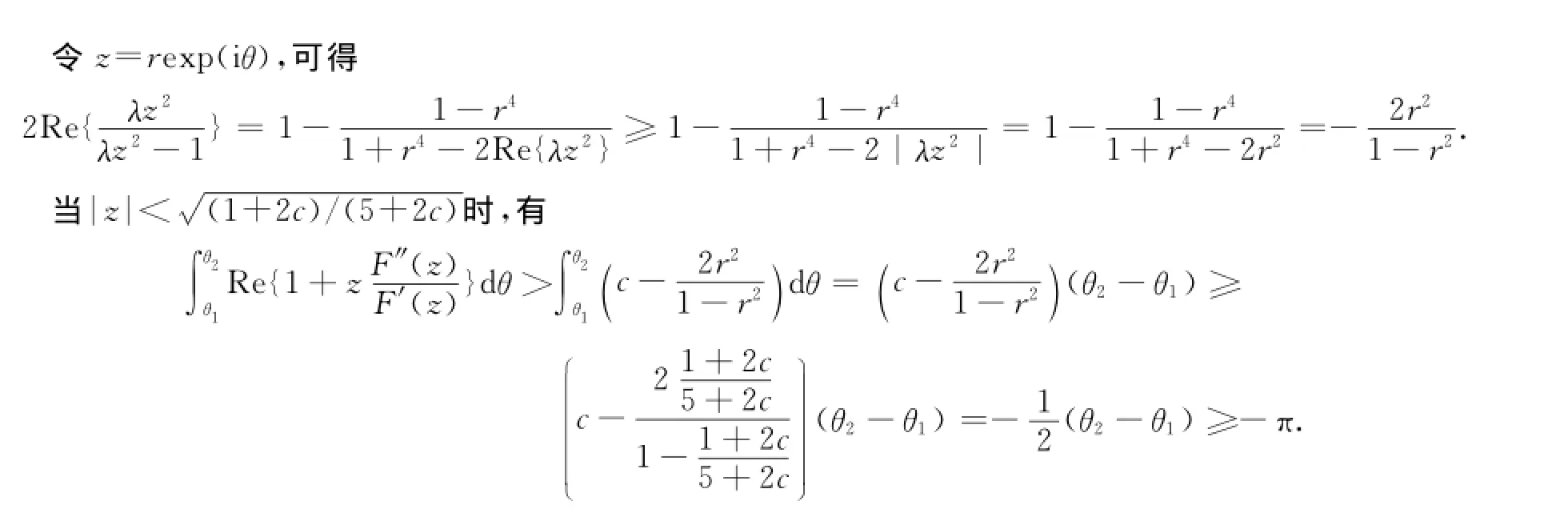
参考文献：

［1］BSHOUTY D，LYZZAIK A.Close－to－convexity criteria for planar harmonic mappings［J］.Complex Analysis and Operator Theory，2011，5（3）：767－774.

［2］MOCANU P T.Injectivity conditions in the complex plane［J］.Complex Anal Oper Theory，2011，5（3）：759－766.

［3］NAGPAL S，RAVICHANDRAN V.On a subclass of close－to－convex harmonic mappings［J］.Complex Variables and Elliptic Equations，2014，59（2）：204－216.

［4］BSHOUTY D，JOSHI S S，JOSHI S B.On close－to－convex harmonic mappings［EB/OL］.［2012－1－11］.http：//dx.doi.org/10.1080/17476933.2011.647002.

［5］BSHOUTY D，LYZZAIK A.Problems and conjectures in planar harmonic mappings［J］.J Analysis，2010，18：69－81.

［7］石擎天，黄心中.调和映照与其剪切函数的单叶性［J］.华侨大学学报：自然科学版，2013，34（3）：334－338.

［8］王其文，黄心中.在微分算子作用下调和函数的单叶半径估计［J］.华侨大学学报：自然科学版，2014，35（2）：227－231.

［9］KAPLAN W.Close－to－convex schlicht functions［J］.Mich Math J，1952，1（2）：169－185.

［10］CLUNIE J，SHEIL－SMALL T.Harmonic univalent functions［J］.Ann Acad Sci Fenn Ser A I Math，1984，9：3－25.

（责任编辑：钱筠 英文审校：黄心中）

On the Analytic Properties and Coefficient Estimate for Close－to－Convex Harmonic Mappings

HUANG Yun，HUANG Xin－zhong
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

Abstract：Research analytic representing formula and coefficient estimates for h（z）with Re0，where his the analytic part of harmonic mappings f（z）＝h（z）＋g（z）that are stable close－to－convex property on unit disk D.If the dilatation function w（z）is a linear function，the stable close－to－convex criterion is proved.The results improve the one made by Shouty and Nagpal.Moreover，we also obtain the stable close－to－convex radius estimate for f＝h＋g珚 withon the unit disk D.

Keywords：harmonic mapping；stable close－to－convex；coefficient estimate；univalent radius

通信作者：黄心中（1957－），男，教授，博士，主要从事函数论的研究.E－mail：huangxz＠hqu.edu.cn.

中图分类号：O 174.51

文献标志码：A

文章编号：1000－5013（2015）04－0478－06

doi：10.11830/ISSN.1000－5013.2015.04.0478

收稿日期：2015－01－05

基金项目：国家自然科学基金资助项目（11471128）；福建省自然科学基金资助项目（2014J01013）