部分充填钢箱－混凝土组合梁受力性能有限元分析

莫时旭，周晓冰，周迎春，张堃（.广西岩土力学与工程重点实验室，广西桂林54004；2.桂林理工大学土木与建筑工程学院，广西桂林54004）



部分充填钢箱－混凝土组合梁受力性能有限元分析

莫时旭1，2，周晓冰1，周迎春1，张堃1
（1.广西岩土力学与工程重点实验室，广西桂林541004；
2.桂林理工大学土木与建筑工程学院，广西桂林541004）

摘要：为了研究部分充填钢箱－混凝土组合梁负弯矩区的受力性能，完成3根简支组合梁构件在跨中两点反向对称荷载作用下的试验.选用合适的单元类型、本构关系及破坏准则，建立以模拟试验梁为对象的非线性模型，得到相应的挠度－荷载曲线和截面应变值，模拟结果与试验结果吻合良好.通过改变梁的一些主要参数，对极限承载力和跨中挠度进行预测.分析表明：若要提高极限承载力和降低跨中挠度，可依次提高梁的配筋率，加厚底板、腹板、顶板和中隔板，也可适当提高混凝土强度.

关键词：钢箱－混凝土组合梁；受力性能；非线性模型；挠度－荷载曲线

钢－混凝土组合梁是由钢梁和混凝土翼板通过抗剪连接件叠合而成的组合结构，能充分利用各自材料的力学性能.与钢结构、混凝土结构相比，它具有承载力高、塑性和韧性良好、经济效益显著、施工方便等特点.由于混凝土材料的不均匀，钢－混凝土组合梁负弯矩区混凝土容易开裂，裂缝的宽度不仅影响结构的外观，而且影响其承载力和耐久性.为此，学者提出一种新型的部分充填钢箱－混凝土组合结构［1］，在钢箱内充填50%的混凝土，改善其结构性能，提高负弯矩区的受力性能.目前，国内外对这种新型结构研究较少，但钢－混凝土组合结构的研究已取得一定成果［2－6］.经历了几十年的发展，有限元方法已趋于完善，非线性问题的各种算法日益成熟，在工程领域得到广泛的应用.有限元求解的基本过程主要包括结构离散化、有限元求解、计算结果的后处理等三个部分.该方法不需要实验场地，能降低设计成本和缩短设计时间，不受环境的影响，改变参数就能得到所需的有限元模型.国内有关学者已对钢－混凝土组合梁模型进行了有限元模拟，并取得了预期的效果［7］.本文利用ANSYS软件对3根部分充填钢箱－混凝土简支梁试件受力性能进行模拟计算分析，验证模型的有效性.

1　试验设计

1.1 试件及材料性能

设计3根不同混凝土翼板配筋率的部分充填式钢箱－混凝土组合结构简支梁，通过两点对称反向加载的加载模式模拟组合梁负弯矩的受力性能.组合梁的截面尺寸相同，长度均为4.4m，梁高为0.42 m.其中：钢箱梁高为0.3m；宽为0.18m；混凝土翼板的厚度为0.12m；宽度为1m；翼板与钢箱采用栓钉连接，其抗剪连接度为1.0.试验梁PSCB1～PSCB3的纵向配筋率分别为1%，2%，3%，横向分布钢筋的的配筋面积为纵向钢筋的20%.钢箱体由钢板板焊接而成，顶板和底板采用10mm Q235钢板，腹板采用4mm Q235钢板，隔板采用4mm Q235钢板.将钢箱分成上下两个箱室，下箱室充填混凝土，上箱室为空室.试件正面及组合梁侧面的投影示意图，如图1，2所示.

混凝土翼板和箱内充填混凝土设计等级均为C40.由于一次性浇筑的混凝土量少，故采用自拌混凝土.水泥选用42.5号的普通硅酸盐水泥，细骨料选用中粗河沙，粗骨料采用级配良好的碎石.为了保证混凝土拌合物的和易性和因混凝土的收缩而与钢箱之间脱空，加入适量的减水剂和膨胀剂.混凝土配合比：水泥∶水∶碎石∶沙＝1∶0.43∶2.92∶1.25.减水剂和膨胀剂分别为水泥的2%，3%.

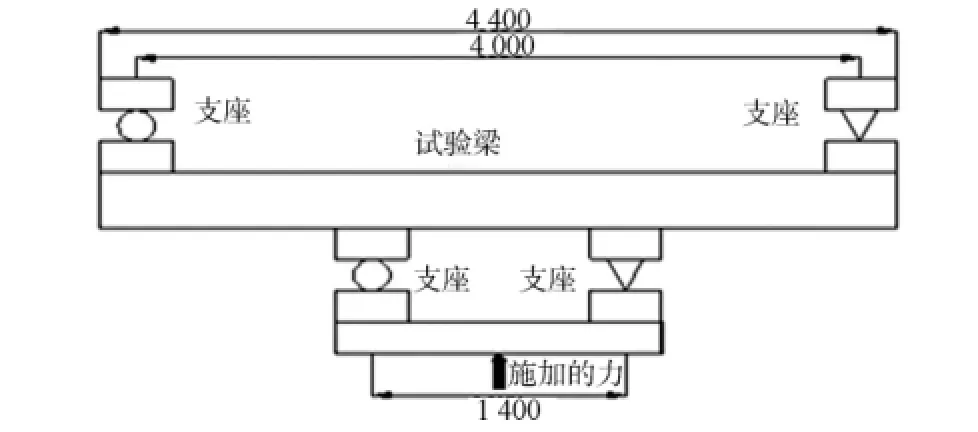
图1　试件正面投影示意图（单位：mm）Fig.1　Front projection of specimen sketch（unit：mm）

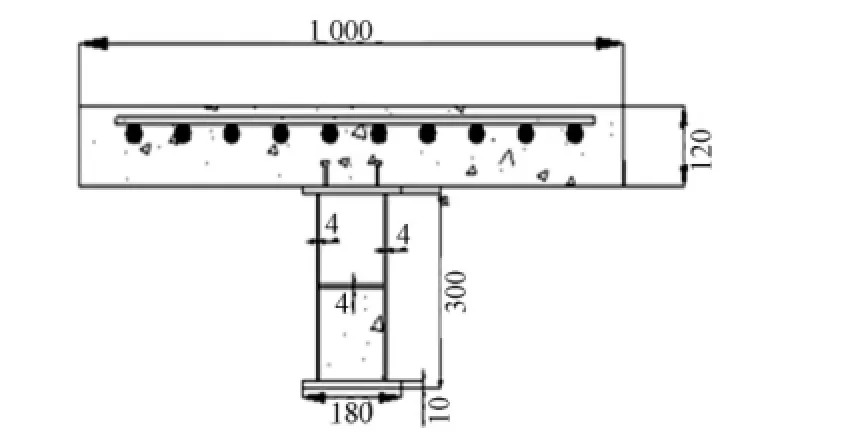
图2　组合梁侧面投影示意图（单位：mm）Fig.2　Side projection of composite beam diagrammatic sketch（unit：mm）

1.2 荷载加载装置及测点布置

使用200t的千斤顶进行反向加载，通过分配梁等分为两个集中荷载对称施加在梁上，计算跨径为1.4m，分级加载，并通过压力传感器进行控制.在跨中处安装百分表，以测量梁的跨中挠度，并由人工逐级记录.为了测量混凝土板裂缝的位置，每隔10cm，用墨斗在翼板的顶面沿梁的横向和纵向弹线形成方格网.随着荷载的增加，用笔芯标定裂缝的开展.

2　有限元模型的建立

2.1 基本假设

部分充填钢箱－混凝土组合结构受力复杂，为使问题简化，做如下4点假设.1）钢箱与混凝土之间的粘接是可靠的，忽略两部分之间的滑移.2）钢材、钢筋采用理想弹塑性本构关系模型.3）不考虑混凝土徐变、收缩等时随效应.4）混凝土板与钢箱之间无相对摩擦，所有剪力均有抗剪连接件传递.

2.2 单元的选择

Solid 65是用于仿真的3D实体结构.元素由8点组合而成，每个节点具有x，y，z位移方向的3个自由度，具有潜变、塑性、膨胀、大变形、大应变、应力强化的特性.当某个单元被压溃或拉裂时，该单元的刚度变为零，单元不起作用，从而模拟构件的破坏［8］.Link 8，Link 10单元可应用于不同工程领域，如桁架、杆件、弹簧等.该元素为三维空间承受单轴拉力－压力，每个节点具有x，y，z位移方向的3个自由度，无法承受力矩，能模拟蠕变、钢筋松弛、应力刚化等特性.Shell单元具有弯曲及薄膜特性，与平面同方向及法线方向的负载皆可承受.元素具有x，y，z位移方向及x，y，z旋转方向的6个自由度.应力强化及大变形的效应也适合该单元.可选择连续性相切矩阵用于大变形（有限的旋转）分析.因此，模型中的翼板混凝土和内填混凝土采用Solid 65单元，钢板采用Shell 181单元，钢筋采用Link 8单元.

2.3 材料本构关系

钢筋采用Higashibata提出的应力－应变关系［9］，取E′＝0.01Es，有

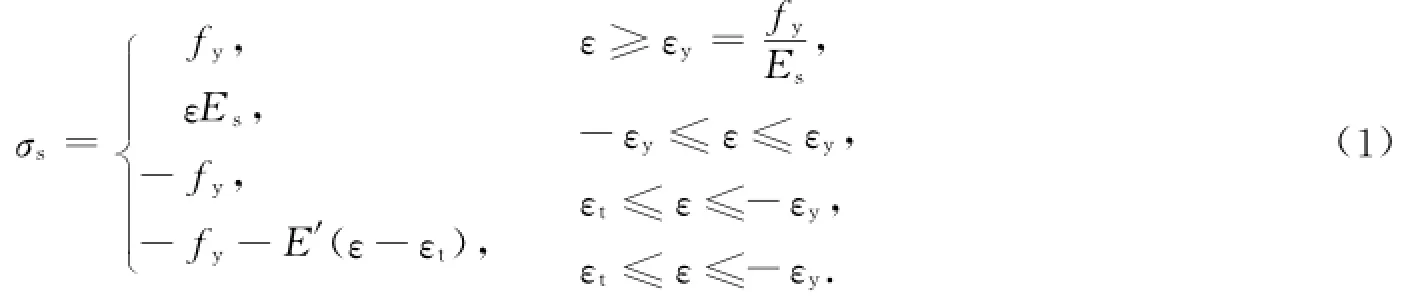
混凝土采用韩林海等［10］建议的以□为主要参数的应力－应变关系，即

有限元计算方案：完全忽略钢箱与混凝土之间的相对位移，两者在受力过程中视为一整体，计算模

图3　有限元模型Fig.3　Finite element model

型中钢板与混凝土界面上共用相同的节点；由于试验出现混凝土的收缩而与钢箱脱空，考虑采用接触单元分析；混凝土采用五参数破坏准则，裂缝张开剪力传递系数为0.5，裂缝闭合剪力传递系数为1.0，混凝土抗拉强度由混凝土强度等级确定关闭压碎判断，拉应力折减系数选用默认值0.6，其余均采用默认值［11］有限元模型，如图3所示.

2.4 荷载的施加、收敛准则

在梁的非线性有限元分析过程中，应力集中使支点或加载点的混凝土过早地出现开裂或压碎破坏，导致有限元分析过程提前终止，模拟失败.因此，在计算机建模时，可以在支点或加载点处设置弹性垫块［10］.模型在荷载分配梁支座下设置弹性垫块，采用Solid 45单元模拟.

采用位移控制法控制收敛.程序的收敛性受子步数的影响，太小或太大都不能达到正常收敛.为了容易收敛，节约运算时间，将收敛精度放宽至5%，每个子步中平衡迭代的最大次数为50次.

3　有限元分析与试验的对比

3.1 荷载位移曲线

开裂弯矩计算值与实测值，如表1所示.表1中：试验开裂荷载为pexp；模拟开裂荷载为pc；试验极限荷载为pexp，u；模拟极限荷载为pc，u.由表1可知：有限元模拟的开裂荷载比实测开裂荷载低，这是因为实测开裂荷载由肉眼可见裂缝而定，偏差（η）在允许范围以内，吻合较好.模拟的极限承载力比试验结果高，这是因为命令流文件中没有考虑混凝土翼缘与钢箱间的滑移，偏差也在允许范围以内，满足要求，挠度－荷载曲线反应了很好的延性.

表1　开裂弯矩计算值与实测值Tab.1　Cracking moment of calculation value and measured value

由有限元分析结果可知：3根简支梁的结果相近.以PFSCB1为例，分析部分填钢箱－混凝土组合梁的受力过程，极限荷载作用下梁的跨中挠度－荷载（f－p）曲线，如图4所示.由图4可知：在弹性阶段，p＜0.3pu，荷载与挠度基本上呈线性关系，有限元曲线与试验曲线吻合良好；在弹塑性阶段，p＜0.8pu，此阶段开始于受压区混凝土板中钢筋的屈服，并伴随着钢箱的局部屈曲；在完全塑性及破坏阶段，即荷载加载至接近极限值时，挠度快速发展，钢箱腹板局部屈曲加快，曲线平缓甚至出现下降段.

由于试验中混凝土板跨中的应变值不理想，因此，文中只给出钢箱跨中顶板、腹板、底板应变－荷载（ε－p）曲线，如图5～7所示.由图5～7可知：模拟结果与试验结果吻合良好，说明所建立的非线性模型是有效的，在设计中可通过参数的改变对所需结果进行预测.

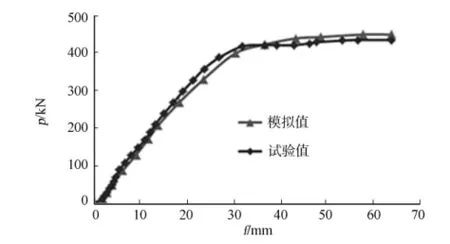
图4　跨中挠度－荷载试验与模拟值比较Fig.4　Comparison between experimental and dsimulation values of mid－span deflection－load

图5　跨中顶板应变－荷载试验与模拟值比较Fig.5　Comparison between experimental and simulation values of mid－span top plate strain－load

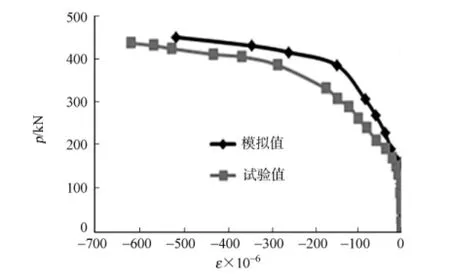
图6　跨中腹板应变－荷载试验与模拟值比较Fig.6　Comparison between experimental andsimulation values of mid－span web－load

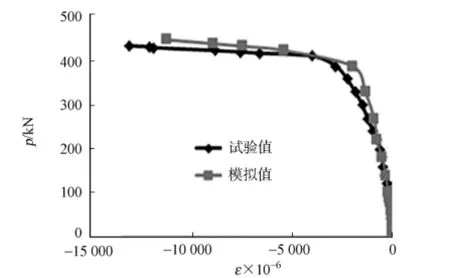
图7　跨中底板应变－荷载试验与模拟值比较Fig.7　Comparison between experimental and simulationvalues of mid－span bottom plate strain－load

4　组合梁参数分析

通过改变部分充填钢箱－混凝土组合梁混凝土强度（C）、配筋率（ρ）、钢箱顶板厚度、中隔板厚度、腹板厚度、底板厚度（l）、钢箱内充填混凝土等参数，得到各参数的变化与梁的极限承载力提高百分比（ηp）的关系.

混凝土强度从C20提高到C45，梁的极限承载力提高的百分比，如图8（a）所示.由图8（a）可知：强度增至C40后，极限承载力提高的速率有所降低，但总体而言，混凝土强度的提高对梁的极限承载力的提升效果较好.

组合梁配筋率从1%提高到5%，梁的极限承载力提高的百分比，如图8（b）所示.由图8（b）可知：随着配筋率的提高，梁的极限承载力增加明显，尤其是在1.5%到2.5%之间；配筋率超过2.5%后，极限承载力提高百分比的速率越来越慢.因此，在设计中若要提高梁的极限承载能力，可选择提高梁的配筋率，但配筋率不宜过高.

钢箱顶板厚度、中隔板厚度、腹板厚度、底板厚度从1mm加厚至8mm，梁的极限承载力提高的百分比，如图8（c）所示.由图8（c）可知：加厚钢箱底板和腹板对提高承载力可达到满意的效果，但加厚中隔板和顶板效果不明显，加厚顶板的效果最差.因此，在满足梁的稳定性的前提下，适当加厚腹板和顶板可提高梁的极限抗载能力.

钢箱内充填混凝土从0%提高到100%，即由空钢箱提高到全充填混凝土，梁的极限承载力提高百分比，如图8（d）所示.由图8（d）可知：钢箱内混凝土提高至60%时，梁的极限承载力最大；70%时出现拐点，之后保持不变，因为随着箱内混凝土的增加，梁的相对受压区保持不变，使部分充填混凝土受拉.

在相同荷载作用下，通过改变部分充填钢箱－混凝土组合梁配筋率、钢箱顶板厚度、中隔板厚度、腹板厚度、底板厚度等参数，得到各参数的变化与梁的跨中挠度降低百分比的关系（ηf）.混凝土强度等级从C20提高至C45，梁跨中挠度降低的百分比，如图9（a）所示.由图9（a）可知：效果并不理想，考虑到对极限承载力的影响，建议混凝土强度采用C40.

组合梁配筋率从1%提高到5%，梁的跨中挠度降低的百分比，如图9（b）所示.由图9（b）可知：配筋率的提高对梁跨中挠度的降低有显著的影响，配筋率在1.5%～4.0%之间，效果尤为明显.因此，结合配筋率变化对极限承载力的影响，建议配筋率在4%左右.

钢箱顶板厚度、中隔板厚度、腹板厚度、底板厚度从1mm加厚至10mm，梁的跨中挠度降低的百分比，如图9（c）所示.由图9（c）可知：加厚底板对降低跨中挠度的效果最好，其次是腹板，中隔板最差.因此，适当加厚底板和腹板最为经济.

钢箱内充填混凝土从0%提高到100%，梁的跨中挠度降低的百分比，如图9（d）所示.由图9（d）可知：充填量从0%提高到10%，跨中挠度下降地最快，因为为了便于浇灌在钢箱内加了一层中隔板；在10%到60%之间基本保持不变.因此，钢箱内充填60%最为合适.

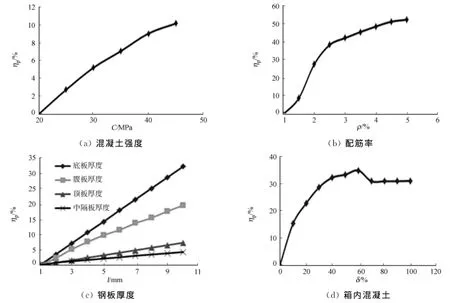
图8　参数变化与极限承载力提高关系Fig.8　Relationship between parameter varation and ultimate bearing capacity increase diagram

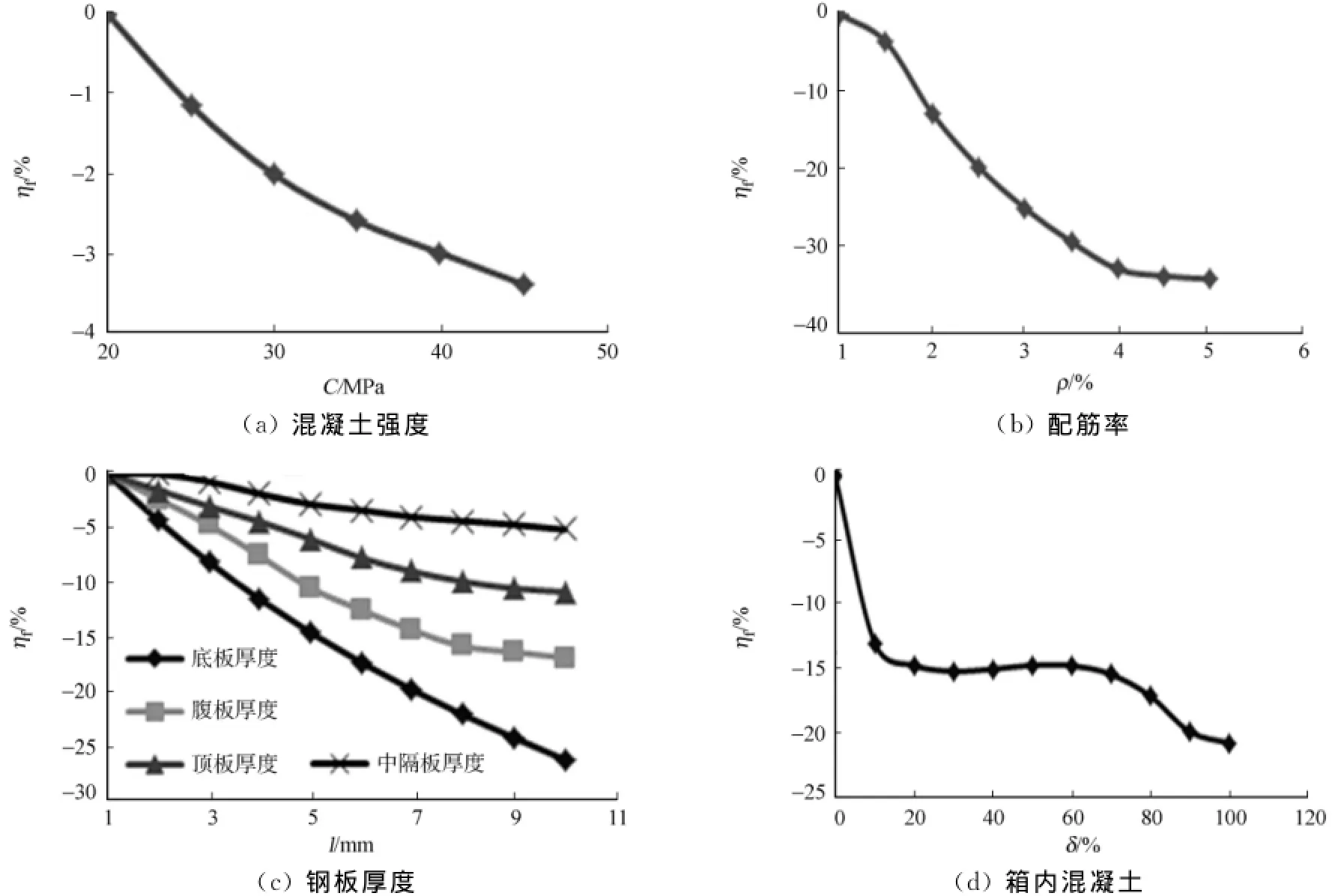
图9　参数变化与跨中挠度降低关系Fig.9　Relationship between parameter varation and cross deflection reduction diagram

5　结论

建立部分充填钢箱－混凝土组合梁有限元模型，对模拟结果与试验结果进行比较，可以得出以下5点结论.

1）模拟结果与试验结果虽然存在一定的偏差，但都在工程误差允许范围之内.

2）由于没有考虑钢箱与混凝土之间的滑移，模拟结果中的极限荷载和模拟值弹性刚度偏大.

3）组合梁受力性能较好，极限承载力和刚度高.

4）通过对梁的各主要参数进行分析可知：配筋率对极限承载力和跨中挠度的影响效率最高；钢板在保证梁的局部稳定的前提下，使用薄的钢板更为合理.建议在对组合梁进行设计时，混凝土强度采用C40，配筋率在4%左右，钢箱内混凝土充填60%.

5）应用有限元软件可以实现对钢箱－混凝土梁的非线性有限元分析，并能得到正确可靠的结果.

参考文献：

［1］NAKAMURAA S I，MOR ISH ITA B H.Bending strength of concrete－fill ednarrow－width steel box girder［J］.Journal of Constructional Steel Research，2008，64：128－133.

［2］张金，周志祥，向红，等.钢－混凝土组合连续梁力学性能分析［J］.中外公路，2012，32（1）：120－125.

［3］解恒燕，郑文忠.内置钢箱－混凝土简支组合梁受力性能试验［J］.哈尔滨工业大学学报，2009，41（2）：37－42.

［4］杨树标.按变刚度计算钢筋混凝土梁挠度［J］.河北煤炭建筑工程学院学报，1992（2）：1－8.

［5］薛伟，胡夏闽，刘加荣.简支钢－混凝土组合梁挠度计算方法的探讨［J］.江苏建筑，2009（125）：29－31.

［6］孙小菲，吴春生.界面滑移效应下钢－混凝土组合梁总剪力和挠度［J］.南昌大学学报：工科版，2007，29（4）：390－394.

［7］刘洋，童乐为，孙波，等.负弯矩作用下钢－混凝土组合梁受力性能有限元分析及受弯承载力计算［J］.建筑结构学报，2014，35（10）：10－20.

［8］周勇.钢筋混凝土梁的非线性有限元分析［J］.国外建材科技，2008，29（3）：22－24.

［9］吕西林，陆伟东.反复荷载作用下方钢管混凝土柱的抗震性能试验研究［J］.建筑结构学报，2000，21（2）：2－11，27.

［10］韩林海，陶忠.方钢管混凝土轴压力学性能的理论分析与试验研究［J］.土木工程学报，2001，34（2）：17－25.

［11］莫时旭，郑艳，钟新谷，等.钢箱－混凝土组合梁受力性能有限元分析［J］.广西大学学报：自然科学版，2010，35（4）：

543－548.

（责任编辑：钱筠 英文审校：方德平）

Finite Element Analysis of Mechanical Performance of Partially Filled Steel Box－Composite Beams

MO Shi－xu1，2，ZHOU Xiao－bing1，ZHOU Ying－chun1，ZHANG Kun1
（1.Key Laboratory of Guangxi Geotechnical and Geotechnics Engineering，Guilin 541004，China；2.College of Civil Engineering and Arcitecture，Guilin University of Science and Technology，Guilin 541004，China）

Abstract：The mechanical performance of partially filled steel box－concrete composite beams was investigated by the experiment of three simple－supported composite beam components under mid－span two－point antisymmetric loads.Suitable element types，constitutive relationship and failure criterion were selected to establish a nonlinear model to simulate the experimental beams.The deflection－load curves and cross－sectional strain values were obtained.The simulation results agree with the obtained experimental results，indicating the validity of finite element model.The bearing capacity and the mid－span deflection can be predicted by some of the major beam parameters.The analysis indicates that the ultimate load bearing capacity and stiffness of beams enhance as reinforcement ratio of girders，thickness of baseboard，web，roof，partition and concrete strength increase.

Keywords：steel box－concrete composite beams；mechanical performance；nonlinear model；deflection and load curve

通信作者：莫时旭（1964－），男，教授，博士，主要从事桥梁工程的研究.E－mail：moshixuwh＠yahoo.com.cn.

中图分类号：TU 321.1；TU 317.1

文献标志码：A

文章编号：1000－5013（2015）04－0455－06

doi：10.11830/ISSN.1000－5013.2015.04.0455

收稿日期：2015－03－17

基金项目：国家自然科学基金资助项目（51168011，51108109）