OHNN新的分组Hash算法

李国刚，钟超林，蔺小梅（华侨大学信息科学与工程学院，福建厦门361021）



OHNN新的分组Hash算法

李国刚，钟超林，蔺小梅
（华侨大学信息科学与工程学院，福建厦门361021）

摘要：在Hash函数算法的研究设计过程中，引入混沌系统理论，探索研究基于混沌动力学的Hash函数算法.将分段线性混沌映射和过饱和的Hopfield神经网络（OHNN）进行结合，提出一种基于混沌动力理论的单向Hash函数构造方法.对算法进行仿真和测试，从不同方面分析验证所提新的算法满足Hash算法的性能指标.安全性分析表明：该算法能抵抗多种碰撞和统计分析的攻击，具有很好的安全性能.

关键词：Hopfield神经网络；混沌吸引子；分段线性映射；Hash算法

采用大量逻辑运算的Hash函数的方法已不具备所需的安全特性［1－6］，当经典Hash函数被攻破后寻找一个更安全的算法就变得不再那么简单.于是，在Hash函数算法的研究设计过程中，引入混沌系统理论［3］，探索基于混沌动力学的Hash函数算法，成了密码学领域研究的新思路.本文将分段线性混沌映射和过饱和Hopfield神经网络（OHNN）进行结合，提出一种基于混沌动力理论的单向Hash函数构造方法.

1　分段线性映射

选择的混沌映射是一维分段线性映射，它从标准帐篷映射和斜帐篷映射推广演化而来，函数为

xn/q，0≤xn＜q，

（xn－q）/（0.5－q），q≤xn＜0.5，（1

（1－x－q）/（0.5－q），0.5≤x＜1－q，

（1－xn）/q，1－q≤xn＜1.

式（1）中：x取值范围为［0，1］；控制参数q取值范围为（0，0.5）.当q在（0，0.5）的范围内时，会产生混沌现象，其函数图形，如图1所示.由文献［6］可知：该分段线性映射的输出序列在（0，1）是遍历的，有着很好的数学统计特性.系统的不变分布函数f＊（x）的算子［5］为

Psf＊（x）＝Pf＊（xP）＋（0.5－P）f＊（P＋x（0.5－P）＋（0.5－P）f＊（0.5＋（1－x）（0.5－P））＋Pf＊（1－xP）.（2）

f（x）＝1表明系统在（0，1）上是均匀分布的.

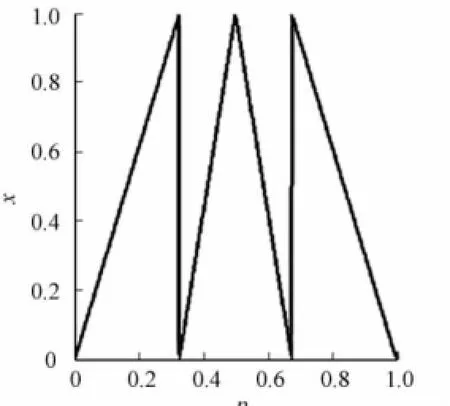
图1　分段线性映射Fig.1　Piecewise linear mapping

2　OHNN吸引子的混沌特性

在OHNN中吸引子［4］在每个稳定状态时候的收敛域是混沌的，其与神经网络的初始状态之间表现出一种不规则的关系，称之为混沌性［5］.假设Hopfield神经网络有N个神经元，算法中取N＝16.引入一随机变换矩阵H，原始状态Su和吸引域中各元素组成的矩阵S的演变规律为式（3）～（4）中：＾S是S的更新状态；＾Su是Su的更新状态.

神经网络新的权值联结矩阵T为式（5）中：H′为H的转置矩阵.

网络运行后，按式（2），（3）的变化规律，当改变混沌神经网络的初值，即T发生改变时，其对应的吸引子和吸引域都都将发生非常明显的改变.基于离散的Hopfield神经网络的统计概率问题，如果要有较多的不可预测的吸引子，则要求网络中兴奋性的突触连接和抑制性的突触连接的数目要尽可能地相等.算法选取N＝16，也是基于此考虑.

设OHNN网络的初始联结矩阵T0与N阶非奇异随机变换矩阵H分别为

3　算法设计

Hash算法结构上一般分为压缩函数和运算迭代.压缩函数承担Hash算法最关键的功能，即如何将任意长度明文序列单向压缩映射成固定长度的输出，设计了一种新的单向分组Hash函数算法.算法的基本思想如下：将OHNN的收敛域中的吸引子元素x0作为密钥，同原始文本比特、分段线性映射（式（4））的上一次迭代结果的值结合一起，共同运算得出对应的Hash值.设计的Hash函数生成的函数值长度（K）为128b.整个算法的结构框图，如图2所示.

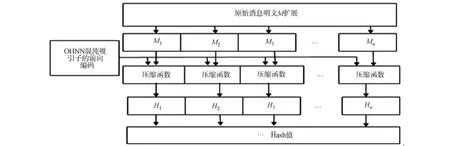
图2　算法结构框图Fig.2　Block diagram of the algorithm

1）明文扩展.明文消息是一段任意长字符，每一个明文字符数值ASCII变换后，转换为［0，1］之间的浮点数.将转换后的数值存储在数组D中.扩展方法如下：设消息明文为m，该消息明文的长度设为s，再添加nb的（101010…）2，使得（m＋n）mod 1 024＝1 024－s成立.s的取值一般为64，0≤n≤Kl.添加后的待处理消息变成M，可分为l个1 024b的子模块，M＝（M1，M2，…，Ml），m＋n＋s＝1 024l.

2）密钥流生成.初始密钥由OHNN和参数H0提供.在OHNN中随机选取吸引域中的一个值的前一状态，将其转换为［0，1］间的浮点数，并将其存储，作为选取的密钥，赋值给xi和H0，作为分段线性映射的初始值.

3）段线性映射处理.算法对明文的迭代处理，采用分组并行处理方式.算法对每一个明文分组子模块Mi（1，2，3，…，l）的处理，采用不同的密钥参数，但采用同样的迭代算法（图2）.以第Mi个模块为例，对于当前所选择的子模块mi，j（j＝1，2，3，…，128），由混沌神经网络产生吸引子的前一个状态作为一个密钥，初始化为当前函数的初始值，经过混沌分段映射函数mi，j次迭代，生产当前状态值xmi，j.然后，将当前生成的混沌状态四舍五入为相对应的0或者1，一直到模块中的所有值都处理完毕，得到的是由Hl 个1或者0组成的数组.通过级联这Kl个0或者1就是第i个模块的Hash值.

4）最终Hash值的生成.每个消息模块Mi（i＝1，2，…，l）都会生成一个中间Hash值Hi（i＝1，2，…，l），最后按H（M）＝H（l）H（l－1）…H（1）计算，得到整个明文序列的最终Hash值.

4　算法测试及安全性能分析

4.1 Hash值分布

混沌Hash函数的主要性能分析方法：固定长度的消息经过Hash函数，通过计算，得到的Hash值能均匀反应消息中每个消息.算法输入的明文序列为

The chip is a communications processor consisting of a reduced instruction set computer processor and a digital signal processor.This device has a rich peripheral set architected specifically for voice over internet protocol phone applications that results in a reduced bill of materials，reduced complexity，and reduced time to develop an internet protocol phone.The chip architecture uses advanced design features to provide flexibility and performance.Combined with Telogy Networks software for IP phone applications，the chip provides a complete hardware/software solution capable of reducing sys－tem design cycle times.

原始明文的ASCII码分布，如图3（a）所示.由图3（a）可知：明文的ASCII都集中在一个小范围之内.算法之后的最终散列值的分布图，如图3（b）所示.由图3（b）可知：经过本Hash函数计算以后的散列值分布相当均匀.

图3　明文信息和Hash值分布Fig.3　Plaintext and Hash value distribution

4.2 文本仿真

仿真采用Hash算法，对一段任意长的原始明文进行计算，获取其十六进制的Hash值H0.对原始明文文本按n（n＞1）种不同的修改方法，修改成与原始明文只有微小差异的n组明文，并计算其对应的Hash值Hn.将文本相关参数做下列6种情况的改变：1）直接计算文本Hash值；2）将首字符T变为Y；3）processor变为orocessor；4）最后字符“.”变为“。”；5）最后位置添加空格符；6）密钥0.232323更改为0.232326.分别得到的Hash值用十六进制表示如下：

1）923A0D309FCE9739325786F0D52F99BD；2）22CA1394803B775095A647053CC9B48B；3）A2647C3D6CC5CEBA28D571DAF0D0E714；4）4AFC27F2E08794EB19A45D4A752BB3C4；5）C814C819818BC3FE89B7884797D03764；6）18DA39BCEA0C8EE77D1D7533988782EF.不同条件下的Hash值，如图4所示.由图4可知：文中构造的Hash算法单项性能良好，任何明文或者秘钥微小的改变都能给最终的结果带来很大的变化，完全符合密码学的混乱的特性.

图4　不同条件下的Hash值Fig.4　Hash values under different conditions

4.3 混乱与扩散性质统计分析

随机选取一段明文并计算出其Hash值H0.然后，随机改变明文中1个比特位的值，计算出改变后的Hash值Hn，比较Hn和H0间不同的比特位个数，完成一次测试统计.重复上述过程N次，得到统计数据.文中测试的Hash算法生成的Hash值长度为128b.测试中N取1 024，如图5所示.由图5可知：每改变明文1b，对应输出的Hash值较为均匀地分布在理论值64b的周边，说明有着较强的混乱和扩散性.对128，256，512，1 024，4种不同测试次数的实验数据进行统计分析，如表1所示.

图5　明文敏感性测试Fig.5　Plaintext susceptibility testing

表1　统计分析测试结果Tab.1　Statistical analysis of the test results

由表1可知：明文每改变1b时，算法的平均变化比特数珚B非常接近于64b的理想值，平均变化概率P也都接近于50%的理想状况；其对应的均方差ΔB和ΔP均非常小，说明变化幅度很小且这种变化是非常稳定的.从统计学的角度说明其具有良好的抗统计攻击的能力.

4.4 抗碰撞分析

文中采用文献［7］的方法，测试算法的抗碰撞能力.经过1 024次试验，得到最大差异度为2 180，最小差异度为853，平均差异度为1 506，平均差异度/字符是88.82，非常接近理想值85.333 3，说明本算法的碰撞程度很低，完全能够抵抗碰撞攻击.

4.5 生日攻击

生日攻击的原理不使用Hash函数和任意代数性质，只决定于消息摘要的长度.为了抵抗生日攻击，通常把消息摘要的长度取为至少128b，对于MD5的生日攻击需要约264次哈希运算，SHA－1输出长度选择的160b也是出于这样的考虑.算法最终的哈希值为128b.

4.6 算法的比较

选取具有代表性的算法［6，8－10］与所提算法进行对比分析，从相关统计数据得出基于混沌的Hash函数均具有很好的统计性能，平均变化比特数达到64b，而同时每比特的平均变化概率50%以上，接近Hash函数算法理论上的理想水平.文中算法与文献［8，10］的算法均具有良好的统计性能，在抗碰撞攻击方面，文中算法在抗碰撞分析中的平均差异度是88.82，而文献［8］所提算法是97.5，明显优于文献［8］所提算法.同文献［6，9］中的平均变化比特数和每比特平均变化概率相比，所设计的算法具有较好的统计性能指标.

5　结束语

提出的基于OHNN的新的分组Hash算法采用并行运算思维，提升了算法执行效率.OHNN的结构和性质满足混沌密码系统的要求，与单纯引入一个混沌系统相比，具有更好的安全性能.即使消息明文的长度相同，只要改H，其对应的吸引子和产生的吸引域则会完全不同.这使分段映射的输入控制参数不一样，引入了扰动，避免混沌动力学特性退化，并确保了最终散列值完全不相同.消息的扩展这一步骤，即把消息长度也作为一个参数项，增加了攻击的难度，使算法的安全性能有了进一步的保障.最后，从不同方面分析验证了所提新的算法满足Hash算法的性能指标.安全性分析表明：本算法能抵抗多种碰撞和统计分析的攻击，具有很好的安全性能.

参考文献：

［1］WANG Xiao－yun，YAO Fang.Cryptanalysis of SHA－l hash function［C］∥Proceedings of Crypto 2005.Berlin：Springer－Verlag，2005：19－35.

［2］XIAO Di，LIAO Xiao－feng，WANG Yong.Improving the security of a parallel keyed hash function based on chaotic maps［J］.Phys Lett A，2009，373（47）：4346－4353.

［3］YANG Gang，YI Jun－yan.Dynamic characteristic of a multiple chaotic neural network and its application［J］.Soft Computing，2013，17（5）：783－792.

［4］LI Guo－gang，GUO Dong－hui.One－way property proof in public key cryptography based on OHNN［J］.Procedia Engineering，2011，15（1/2）：1812－1816.

［5］LASOTA A，MACKEY M C.Probabilistic properties of deterministic systems［M］.Cambridge：Cambridge University Press，1985：1.

［6］XIAO Di，LIAO Xiao－feng.One－way Hash function construction based on the chaotic maps with changeable－parameter［J］.Chaos Solitons and Fractais，2005，24（1）：65－71.

［7］WONG K W.A combined chaotic cryptographic and hashing scheme［J］.Physics Letters A，2003，307（5/6）：292－298.

［8］李永华.混沌加密算法与Hash函数构造研究［D］.大连：大连大学，2012：45.

［9］WANG Yong，LIAO Xiao－feng，XIAO Di，et al.One－way hash function construction based on 2Dcoupled map lattices［J］.Information Sciences，2008，178（5）：1391－1406.

［10］XIAO Di，LIAO Xiao－feng，DENG Shao－jiang.Parallel keyed hash function construction based on chaotic maps［J］.Phys Lett A，2008，372（26）：4682－4688.

（责任编辑：陈志贤 英文审校：吴逢铁）

New Gouping Hash Agorithm Based on OHNN

LI Guo－gang，ZHONG Chao－lin，LIN Xiao－mei
（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

Abstract：In the design process of the Hash function algorithm study，the chaotic systems theory，is introduced to investigate the Hash Function Algorithm Based on Chaos Dynamics.Combining the piecewise linear chaotic map and oversaturated Hopfield neural network（OHNN）.An unidirectional Hash function construction method based on chaotic dynamical theory is proposed.The new algorithm is verified to meet the performance index of Hash algorithm from different aspects by simulation and testing.Security analysis shows that the proposed algorithm can resist many kinds of attacks，and has good security performance.

Keywords：hopfield neural；the chaotic attractor；piecewise linear mapping；Hash algorithm

通信作者：李国刚（1973－），男，教授，博士，主要从事集成电路设计与信息安全的研究.E－mail：lgg＠hqu.edu.cn.

中图分类号：TN 918.4

文献标志码：A

文章编号：1000－5013（2015）04－0393－06

doi：10.11830/ISSN.1000－5013.2015.04.0393

收稿日期：2014－12－29

基金项目：国家自然科学基金资助项目（61370007）；华侨大学科研基金资助项目（14BS115）