基于有效信息重构的故障旋转机械振动加速度信号积分方法

基于有效信息重构的故障旋转机械振动加速度信号积分方法

朱勇1,2姜万录1,2郑直1,2胡浩松1,2

1.燕山大学河北省重型机械流体动力传输与控制重点实验室，秦皇岛，066004

2.先进锻压成形技术与科学教育部重点实验室(燕山大学)，秦皇岛，066004

摘要:提出一种基于有效信息重构的故障旋转机械振动加速度信号积分方法。该方法首先利用集总经验模态分解(EEMD)对积分信号进行分解,然后将峭度指标、均方差值和奇异值组合成特征向量对分解信号进行有效特征提取,并通过欧氏距离搜索提取分解信号中隐含的有效特征分量,最后通过阈值限定将有效特征分量进行叠加重构得到所需有效积分信号。仿真分析和实测数据结果表明，该方法在去除噪声和保留有效特征信息方面，比传统积分方法具有更高的精度和优越性。

关键词:振动加速度;时域积分;频域积分;频域-时域混合积分;有效信息重构

中图分类号:TH13;TP27

收稿日期：2014-07-16

基金项目:国家自然科学基金资助项目(51475405);国家重点基础研究发展计划(973计划)资助项目(2014CB046405);河北省自然科学基金资助项目(E2013203161,E2013203114);河北省研究生创新资助项目(00302-6370002)

作者简介：朱勇,男,1986年生。燕山大学机械工程学院博士研究生。主要研究方向为故障诊断与智能信息处理、机械系统非线性动力学理论及控制。姜万录(通信作者)，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。郑直,男,1985年生。燕山大学机械工程学院博士研究生。胡浩松,男,1989年生。燕山大学机械工程学院硕士研究生。

Useful Information Reconstruction-based Vibration Acceleration

Signal Integral Method for Faulty Rotating Machinery

Zhu Yong1,2Jiang Wanlu1,2Zheng Zhi1,2Hu Haosong1,2

1.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission

and Control,Yanshan University,Qinhuangdao,Hebei,066004

2.Key Laboratory of Advanced Forging & Stamping Technology and Science

(Yanshan University),Ministry of Education of China,Qinhuangdao,Hebei,066004

Abstract:A faulty rotation machinery vibration acceleration signal integration method was proposed based on useful information reconstruction.Firstly,ensemble empirical mode decomposition(EEMD) was utilized to decompose the integral signals.Secondly,the values of kurtosis,mean square error and singular value were proposed to be combined into a feature vector,and further used to extract the effective feature for the decomposed signals.Then,the effective feature components were extracted by Euclidean distance search.Finally,the effective feature components were reconstructed by threshold limit,and the desired integral signals were obtained.The effectiveness and practicability of the method were testified by simulation analysis and measured data.Results indicate that this method is excellent at removing noise and reserving effective feature information,and possesses high precision and superiority.

Key words:vibration acceleration;time domain integral；frequency domain integral；frequency-time domain mixed integral;useful information reconstruction

0引言

在机械故障诊断和状态监测中，常用到加速度、速度和位移三种振动参量。目前，在振动信号测试中，由于加速度传感器具有体积小、频率范围宽、安装方便等众多优点因而其应用更加广泛。然而,在许多行业中往往又需要速度和位移信息，因此就涉及加速度信号积分问题，该过程可以通过硬件或软件来实现[1]。但是硬件积分对积分器性能要求较高，会大大增加测试成本。目前随着数据处理技术的发展，软件积分开始逐渐得到推广应用[2]。

目前，软件积分主要有时域积分和频域积分两类，且国内外有关这两类方法的研究多着眼于去除低频趋势项，但无论是时域积分中的基线校正[3]、高通滤波[4]、曲线拟合[5],还是频域积分中的低频分量置零[6],在实际应用中都存在噪声干扰的影响,当噪声较强时所得结果存在较大误差,积分精度都还需要进一步提高[1]。

本文重点针对故障旋转机械振动信号的特点，提出一种基于有效信息重构的振动加速度信号积分方法,很好地解决了困扰传统积分方法的趋势项和噪声等无效信号的干扰问题。仿真分析和实测数据结果验证了该方法的有效性和可行性。

1有效信息重构积分原理

对于故障旋转机械来说，信号的有效成分主要包括：转频分量、故障特征频率分量以及二者倍频或分频分量的叠加。这就意味着,在故障旋转机械的振动信号分析中,研究者所关注的是数量有限的有效信号分量，而其他的成分可以视作无效干扰予以去除[1]。基于此,本文提出一种基于有效信息重构的故障旋转机械振动加速度信号积分方法。该方法的流程图如图1所示。

图1　基于有效信息重构的信号积分流程

其详细步骤如下：

(1)第一次零均值处理。积分之前先采用零均值处理方法去除原始加速度信号中的直流分量。

(3)第二次零均值处理。采用零均值处理方法对频域积分后的速度时域信号进行处理，去除速度信号中的直流分量。

(4)第一次集总经验模态分解(ensemble empirical mode decomposition,EEMD)可以将非线性、非平稳信号从高频至低频分解为具有不同振动模态的本征模态函数(intrinsic mode function,IMF)和一个剩余项(Rn),因而可以将信号中的有效成分和噪声成分分离,并且分解是自适应的,得到的各IMF分量具备完整性与正交性，可用来实现波形校正。同时,EEMD有效地解决了传统经验模态分解的模态混叠问题[8]。本步骤充分利用EEMD在信号处理方面的优势,将信号分解为若干个IMF分量和剩余项Rn。

(5)第一次特征分量提取。峭度能反映振动信号的分布特性,对冲击信号特别敏感,可定量描述振动信号的冲击水平[9]。均方差能反映一组数据集组内个体间的离散程度，可定量描述计算的精确度[10]。奇异值能反映有用信号和噪声的能量分布情况，信号经奇异值分解(singular value decomposition,SVD)后所得的奇异值中，较大的奇异值主要反映有用信号，较小的奇异值则主要反映噪声。通过SVD可以实现去噪，且消噪结果具有波形失真小、信噪比高等优点[11]。本步骤充分利用峭度值、均方差值、最大奇异值在信号特征提取方面的优势，将三者组合成特征向量T=(a,b,c)T。计算经步骤(4)所得到的n个IMF分量的特征向量Tvi=(avi,bvi,cvi)T(i=1,2,…,n)以及经步骤(3)获得的速度信号的特征向量Tv=(av,bv,cv)T,并分别计算二者之间的欧氏距离di:

(1)

di越小说明其对应的IMF分量中包含的与步骤(3)获得的速度信号有关的有效特征信息越多。

(6)速度信号重构。根据实际需要设定阈值X，通常95%≤X≤100%,X取值越大,则重构信号中包含的有效特征信息越多。按di值由小到大的顺序进行搜索并提取出其对应的IMF分量依次进行叠加重构,同时计算重构后的速度信号与步骤(3)获得的速度信号之间的互相关系数Y。若Y≥X,则停止增加新的IMF分量。剩余较大di值对应的未参与重构的IMF分量和残余分量Rn可以视为噪声干扰予以去除。

(7)时域积分。由众多研究成果可知[12-13],频域二次积分受低频误差影响较大，时域二次积分会产生较大的累积误差。而频域一次积分受低频误差影响较小，时域一次积分产生的累积误差也较小。为了克服频域、时域二次积分的不足，本文在计算位移信号时采用频域-时域混合积分法，即在求位移的两次积分中仅在频域内进行一次，剩下一次在时域内进行。运用Simpson算法[13]对步骤(6)重构后的速度信号心进行时域一次积分，得到位移时域信号。

(8)第三次零均值处理。采用零均值处理方法对时域积分后的位移时域信号进行处理,去除位移信号中的直流分量。

(9)第二次EEMD。利用EEMD将经过步骤(8)处理后的位移信号分解为若干个IMF分量和余项Rn。

(10)第二次特征分量提取。计算步骤(9)得到的各IMF分量的特征向量Txi=(axi,bxi,cxi)T及步骤(8)获得的位移信号的特征向量Tx=(ax,bx,cx)T,并分别计算二者之间的欧氏距离di。

(11)位移信号重构。按di值由小到大的顺序进行搜索并提取其对应的IMF分量依次进行叠加重构,同时计算重构后的位移信号与步骤(8)获得的位移信号之间的互相关系数Y。若Y≥X,则停止增加新的IMF分量。

2仿真分析

仿真一种在复杂耦合故障作用下的旋转机械振动情况,信号转频为30Hz,除了发生以分频和倍频为主要特征的自激振动以外,还伴随有动静碰摩故障[1],同时还含有直流分量。该振动加速度信号表达式为

a(t)=0.04cos(2π·6t+130π/180)+

0.26cos(2π·30t+18π/180)+

0.18cos(2π·60t+43π/180)+

0.064cos(2π·90t+77π/180)+

0.028cos(2π·120t+118π/180)+0.01

(2)

根据香农采样定理，取信号的采样频率为1024Hz，采样点数为1024。为了更接近实际，根据信号强度，以信噪比10dB添加高斯白噪声。

下面分别采用传统积分和本文所提积分方法对仿真信号进行分析，并对结果进行误差评价。

2.1时域积分

(a)速度曲线

(b)位移曲线 图2　时域积分结果

采用零均值处理方法对含噪加速度信号进行去除直流分量处理，并用最小二乘法去除积分结果的趋势项，结果如图2所示。时域积分经过上述处理后,低频趋势得到了很好的抑制,但是噪声干扰对结果的影响仍然很大，导致积分结果仍然存在较大误差，随着积分次数的增加，误差累积效应也更加凸显，位移信号发生了明显的失真。

2.2频域积分

对含噪加速度信号进行频域积分时,将低于3Hz的低频分量置零以消除低频噪声及趋势项的干扰，结果如图3所示。频域积分经过置零处理，低频趋势得到了很好的抑制，但是噪声对结果的影响仍然存在，导致位移信号存在明显的误差。

(a)速度曲线

(b)位移曲线 图3　频域积分结果

2.3有效信息重构积分

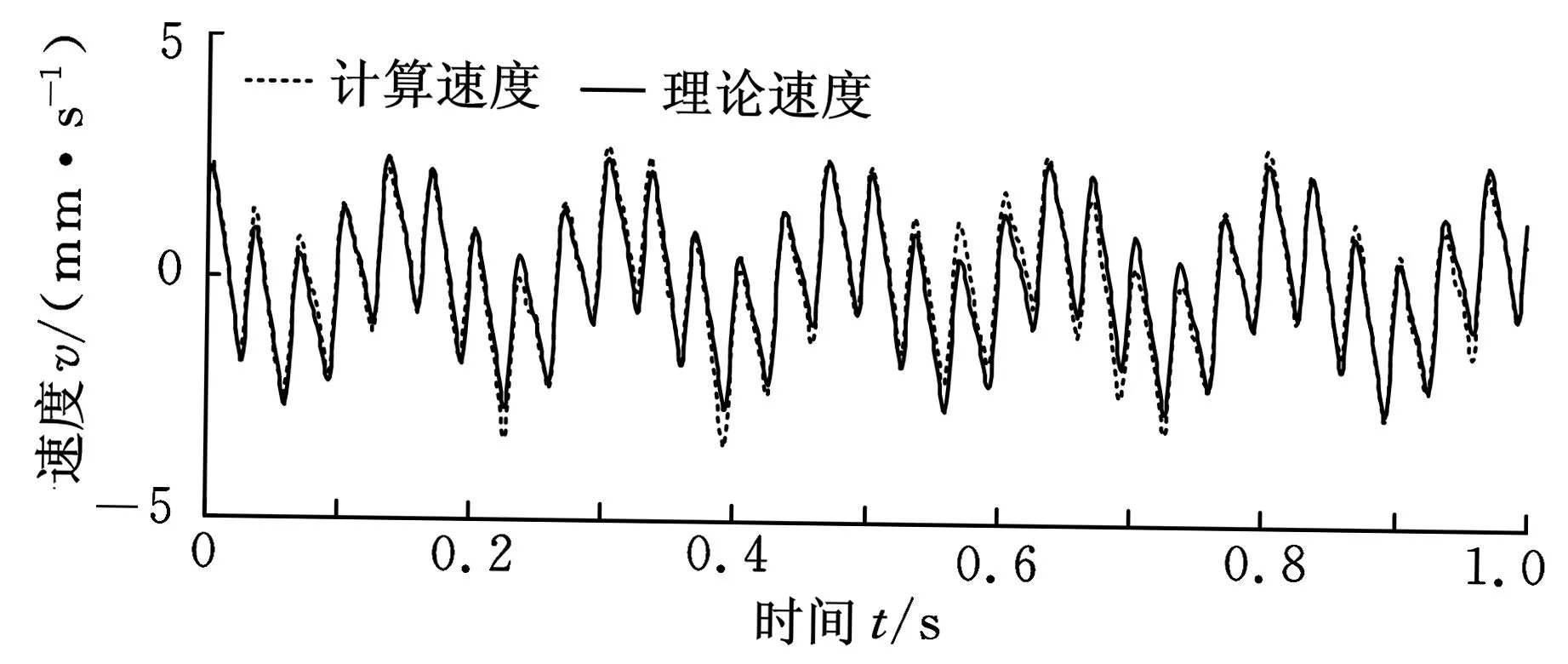
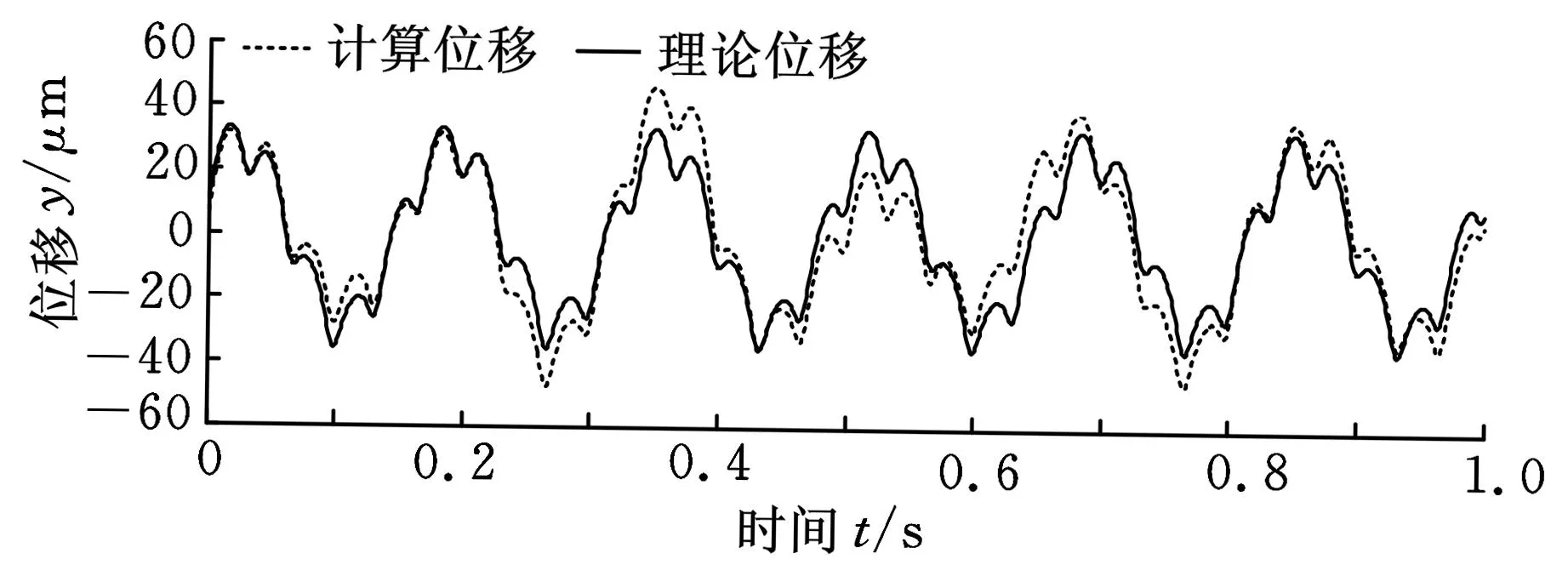
按照本文所提方法对含噪声的加速度信号进行积分，结果如图4所示。相比于各种传统积分方法，采用本文方法得到的结果与理论信号的拟合程度最高。

(a)速度曲线

(b)位移曲线 图4　有效信息重构积分结果

为了对计算结果的精度进行定量的评价,在参考相关文献的基础上,本文引入了平均峰值误差、平均最大相对误差及平方和误差[1,12]三个参数作为评价指标，评价结果如表l和表2所示。

表1　积分速度误差

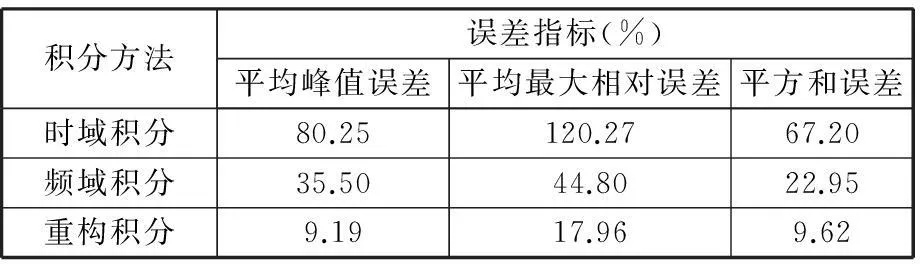
表2　积分位移误差

由表1和表2可知,本文方法的积分精度高于传统的时域、频域积分方法,而且误差不会随积分次数的增加而发生明显的增大,误差累积效应得到有效抑制。说明在对旋转机械的振动信号进行积分时，本文方法具有较高的积分精度和可靠性，结果因噪声等干扰因素产生的失真也较小。

3实验数据分析

为了进一步验证本文方法的有效性,以旋转机械中常用的滚动轴承为研究对象,并通过对美国Case Western Reserve大学滚动轴承故障模拟实验台实测数据[14]进行处理。测试轴承型号及详细参数如表3所示。

表3　6205-2RS JEM SKF型轴承参数

3.1不同故障类型数据分析

本节主要采用驱动端轴承损伤点剥落直径为0.1778mm、深度为0.2794mm时的故障数据作为样本进行分析。采样频率为12kHz,采样点数为8400。根据轴承故障特征频率表达式及表3中相关参数得出，在电机转速为1797r/min时,转轴频率约为30Hz,轴承外圈和内圈的故障特征频率分别约为107Hz、162Hz。

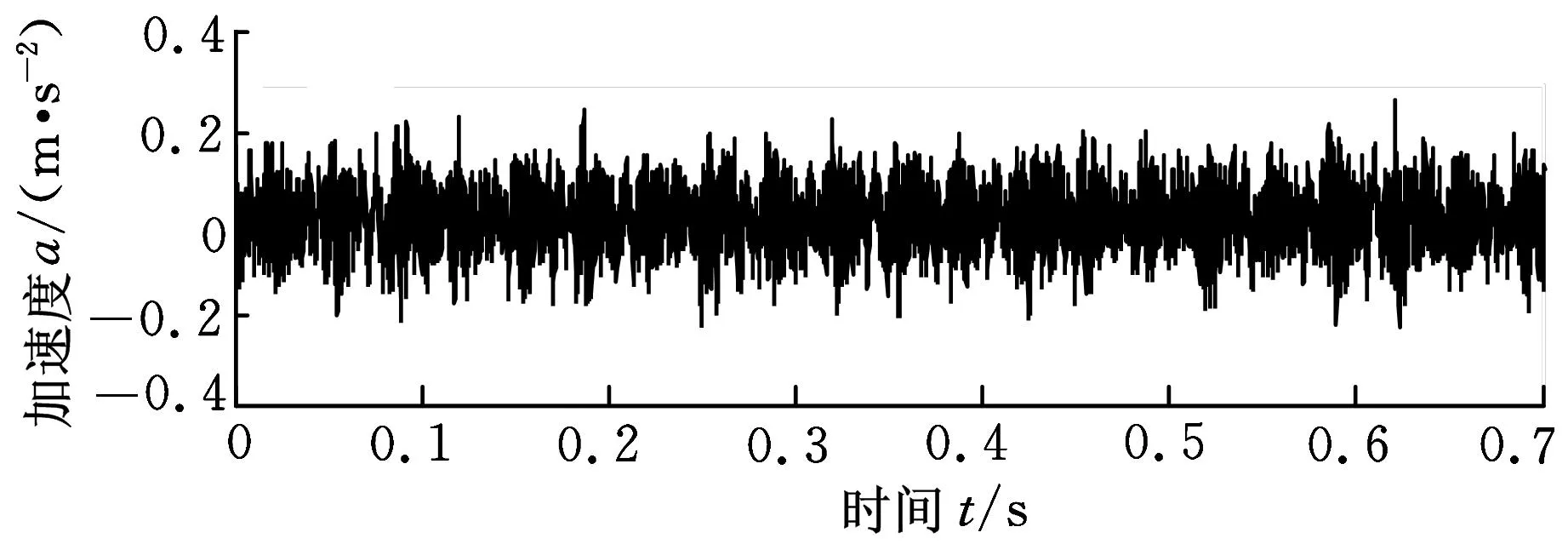
图5所示为该轴承在正常状态、外圈故障状态、内圈故障状态下的振动加速度信号时域波形。由于信号中混入强噪声，从时域信号中很难识别出与故障相关的脉冲成分。目前常用的解决方法是将信号经过滤波处理后转换到频域，从频谱图中通过识别故障频率来判定故障类型。

(a)正常状态

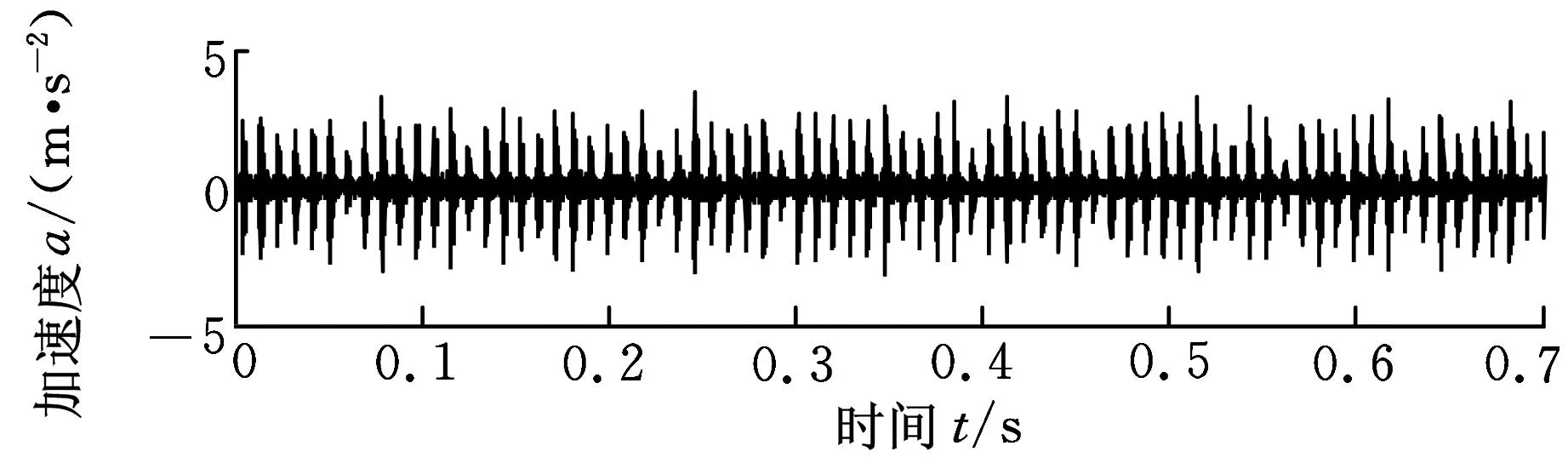
(b)外圈故障

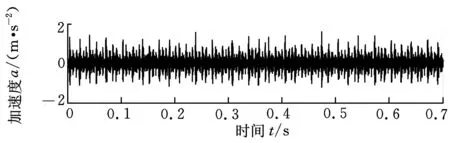
(c)内圈故障 图5　不同故障类型振动加速度信号时域波形

图6为上述三种状态振动加速度信号经过小波消噪处理后对应的局部幅值谱图。为了清晰地比较不同方法的积分效果并准确地判断故障类型，根据前面计算的特征频率,截取20～200Hz频段作重点分析,该频段范围可以完全包含1倍频特征频率30Hz、107Hz、162Hz[15]。

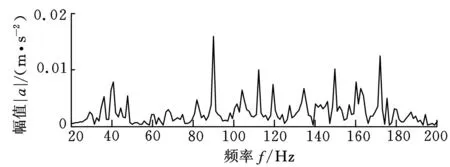
(a)正常状态

(b)外圈故障

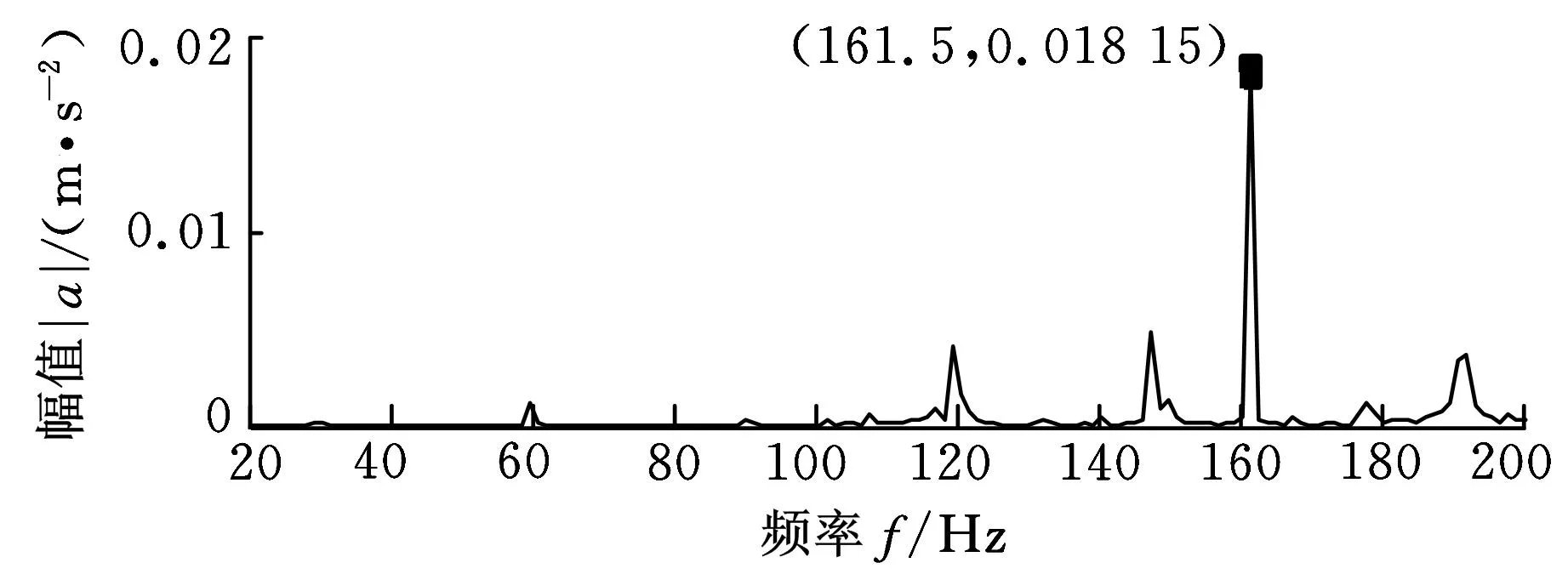
(c)内圈故障 图6　经小波消噪处理后的加速度信号幅值谱图

由图6可知,正常信号的幅值谱图中在转轴基频30Hz及其倍频处有尖峰出现;外圈故障信号在故障特征频率107Hz处有尖峰出现,在162Hz处亦有尖峰出现,这可能由于滚动体与外圈损伤点接触时同时对内圈造成冲击导致的;内圈故障信号在故障特征频率162Hz处有尖峰出现。说明经过小波消噪处理后的信号中有效地包含了故障信息,从信号幅值谱图中可以直观地判断出故障类型。但同时也可看出，由于强噪声的影响,信号中的噪声并没有完全被消除,正常信号的幅值谱图中有杂波出现,外圈和内圈故障信号在转轴基频30Hz及其倍频处的特征频率几乎被淹没。

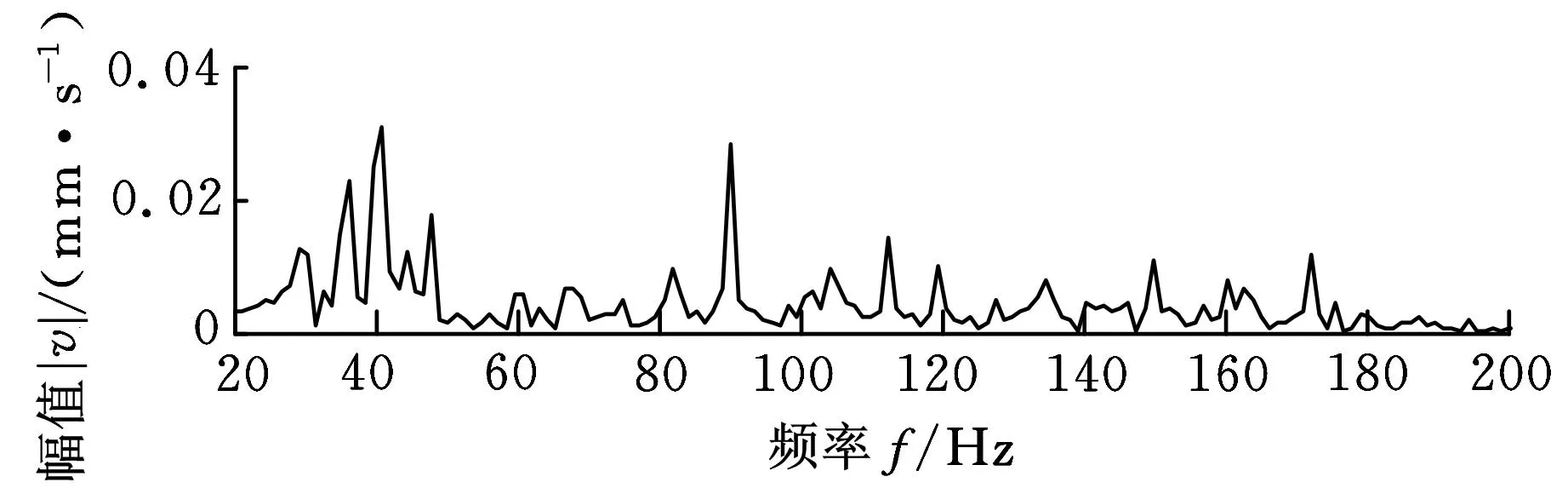
现利用本文提出的有效重构积分方法对上述三种状态振动加速度信号进行处理，并转换到频域进行分析，所得结果如图7、图8所示。

(a)正常状态

(b)外圈故障

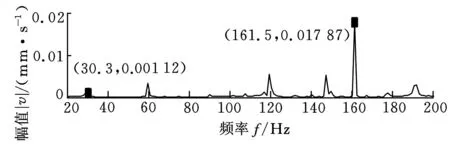
(c)内圈故障 图7　有效信息重构积分结果(速度信号)

由图7、图8可知,正常信号的幅值谱图中杂波得到了有效的抑制;故障信号在转轴基频30Hz及其倍频处的特征频率得到较好的呈现,故障特征频率107Hz和162Hz被清晰地展现,可以有效地判断出故障类型。说明经过本文方法处理后得到的速度信号和位移信号中均有效地包含了有用的故障信息,从复杂的振动信号中准确地提取到了其中隐藏的特征信息,进而验证了该方法的有效性。

(a)正常状态

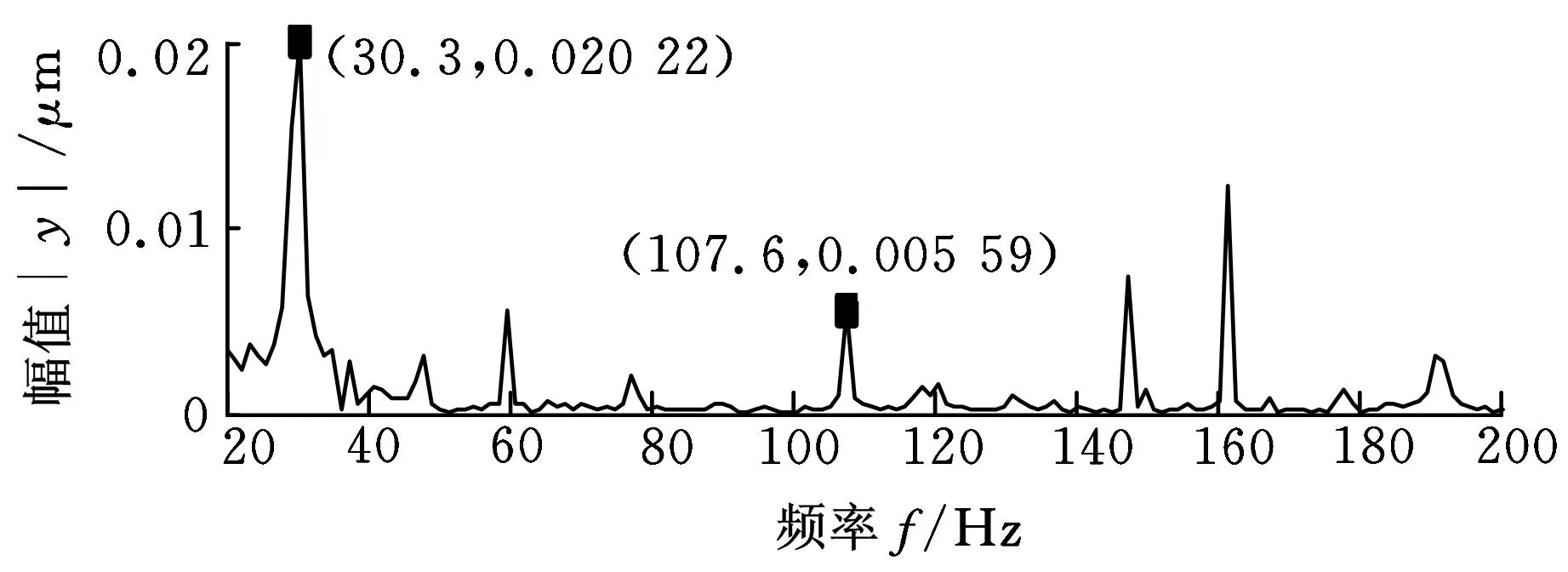
(b)外圈故障

3.2同一故障类型不同故障程度数据分析

为了进一步验证本文方法在分析同一故障类型不同故障程度实验数据时的有效性，本节采用驱动端轴承内圈损伤点剥落直径分别为0.1778mm (故障程度1)、0.3556mm (故障程度2)、0.5334mm (故障程度3)，深度均为0.2794mm时的数据作为样本进行分析。采样频率为12kHz,采样点数为8192。在电机转速为1750r/min时,转轴旋转频率约为28Hz,轴承内圈的故障特征频率约为158Hz。

图9所示为轴承在上述三种不同故障程度下的振动加速度信号时域波形。采用本文方法对其进行处理,所得振动位移信号幅值谱图如图10所示。

(b)故障程度2

(c)故障程度3 图9　不同故障程度振动加速度信号时域波形

(a)故障程度1

(b)故障程度2

(c)故障程度3 图10　不同故障程度振动位移信号幅值谱图

由图10可知，故障信号的转轴基频及故障特征频率得到较好的呈现，且特征频率幅值随着故障程度的增加而增大。说明本文方法从复杂的振动信号中准确地提取到了有用的故障特征信息,从而进一步验证了该方法的实用性。

4结论

(1)本文所提出的基于有效信息重构的信号积分方法充分考虑了振动信号的结构特性,且建立在传统频域、时域积分方法的基础之上，容易实现，具有较强的实用性。研究成果可为设备故障诊断及状态监测特征参数特取提供依据。

(2)本文所提方法充分利用了EEMD在处理平稳信号方面的自适应滤波特性和波形校正特性，并融合峭度指标、均方差值和奇异值分解在信号特征提取方面的优势，通过欧氏距离搜索和阈值限定准确提取出了振动信号中隐含的有效特征分量，精确重构出了所需的积分信号。

(3)在计算位移信号时,采用频域-时域混合积分的形式,有效地克服了传统的时域二次积分会产生较大累积误差、频域二次积分会产生较大低频误差的弊端，积分精度更高。

(4)在积分过程中通过对信号结构的分析，经由波形校正和特征向量搜索获取信号的精确有效分量。在此基础上实施的信号积分和重构运算很好地解决了困扰传统积分方法的趋势项和噪声等无效信号的干扰问题，有效地提高了积分精度。

需要指出的是，由第2节仿真分析结果可知，本文所提方法在信号的平滑段具有较好的精确性，但在信号幅值突变处的积分结果与理论值仍有一定的误差，造成这种差异性的原因主要在于：采用的Simpson求积公式是有3个等距节点的插值型求积公式，虽然这是目前计算定积分近似值的常用有效方法，但是其在数值突变点处的计算结果仍存在较大误差，计算精度还有待于进一步提高。因此，为了获得更高精度的积分结果，需要探索具有更细剖分和更多求积节点的求积公式，以减小在数值突变点处的计算误差。关于求积公式的改进方法,是一个值得长期研究的方向，需要进一步深入探究。

参考文献:

[1]温广瑞,李杨,廖与禾,等.基于精确信息重构的故障转子系统振动加速度信号积分方法[J].机械工程学报,2013,49(8):1-9.

Wen Guangrui,Li Yang,Liao Yuhe,et al.Faulty Rotor System Vibration Acceleration Signal Integration Method Based on Precise Information Reconstruction[J].Journal of Mechanical Engieering,2013,49(8):1-9.

[2]顾名坤,吕振华.基于振动加速度测量的振动速度和位移信号识别方法探讨[J].机械科学与技术,2011,30(4):522-526.

Gu Mingkun，Lü Zhenhua.Discussion of Vibration Velocity and Displacement Signal Identification Method Based on the Vibration Acceleration Measurement[J].Mechanical Science and Technology,2011,30(4):522-526.

[3]Yang J,Li J B,Lin G.A Simple Approach to Integration of Acceleration Data for Dynamic Soil-structure Interaction Analysis[J].Soil Dynamics and Earthquake Engineering,2006,26(8):725-734.

[4]Hong Y H,Park H W,Lee H S.A Regularization Scheme for Displacement Reconstruction Using Acceleration Data Measured from Structures[D].Seoul:Seoul National University,2007.

[5]周小祥,陈尔奎,吕桂庆,等.基于数字积分和LMS的振动加速度信号处理[J].自动化仪表,2006,27(9):51-53.

Zhou Xiaoxiang,Chen Erkui,Lü Guiqing,et al.The Processing of Vibration Acceleration Signal Based on Numeric Integration and LMS[J].Process Automation Instrumentation,2006,27(9):51-53.

[6]李强,王太勇,胥永刚.基于频域积分的振动参量转换修正算法[J].组合机床与自动化加工技术,2005(9):60-61.

Li Qiang,Wang Taiyong,Xu Yonggang.The Modification of the Vibration Parameter Transform Based on Frequency Domain Integration[J].Modular Machine Tool & Automatic Manufacturing Technique,2005(9):60-61,65.

[7]董礼,廖明夫,杨坤记.振动信号频域积分的滤波修正算法[J].机械设计与制造,2010(1):46-48.

Dong Li,Liao Mingfu,Yang Kunji.Filtering Modification of Vibration Signal Integration Algorism[J].Machinery Design & Manufacture,2010(1):46-48.

[8]Wu Z H,Huang N E.Ensemble Empirical Mode Decomposition:a Noise Assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[9]McDonald G L,Zhao Q,Zuo M J.Maximum Correlated Kurtosis Deconvolution and Application on Gear Tooth Chip Fault Detection[J].Mechanical Systems and Signal Processing,2012,33:237-255.

[10]Ni J G,Chen X P.Steady-state Mean-square Error Analysis of Regularized Normalized Subband Adaptive Filters[J].Signal Processing,2013,93(9):2648-2652.

[11]Lehtola L,Karsikas M,Koskinen M,et al.Effects of Noise and Filtering on SVD-based Morphological Parameters of the T Wave in the ECG[J].Journal of Medical Engineering and Technology,2008,32(5):400-407.

[12]蒋良潍,姚令侃,吴伟.边坡振动台模型实验动位移的加速度时程积分探讨[J].防灾减灾工程学报,2009,29(3):261-266.

Jiang Liangwei,Yao Lingkan,Wu Wei.Time History Integration Method of Acceleration from Shaking Table Model Test about Displacement on Side Slope[J].Journal of Disaster Prevention and Mitigation Engineering,2009,26(3):261-266.

[13]王建锋,马建,马荣贵,等.动位移的加速度精确测量技术研究[J].计算机科学,2010,37(12):201-202.

Wang Jianfeng,Ma Jian,Ma Ronggui,et al.Study on Calculation of Dynamic Displacement from Time-frequency Integration of Acceleration[J].Computer Science,2010,37(12):201-202.

[14]The Case Western Reserve University Bearing Data Center.Bearing Data Center Fault Test Data[EB/OL].[2014-07-03].http://csegroups.case.edu/bearingdatacenter /home.

[15]Zhu Y,Jiang W L,Kong X D,et al. An Accurate Integral Method for Vibration Signal Based on Feature Information Extraction[J].Shock and Vibration,2015,2015:1-13.

(编辑卢湘帆)