生活中的勾股定理

吴敏

一、 古代生活中勾股定理的应用

相信同学们都知道大禹治水，相传在夏禹王治水时，就已发现勾股定理，并已把它应用于简易的水利测量，这当然只是传说，当时的历史文献并无确切的记载，直到公元前1世纪（西汉）的《周髀算经》上才有记载.我们数学教材中86页也提到了《九章算术》中的折竹抵地问题.由此不难看出该定理在古代生活中便多有运用.

例1   仕女荡秋千

我国明代有一位杰出的数学家程大位，在他所著的《直指算法统宗》里还有一道“荡秋千”的题：

荡秋千

平地秋千未起，踏板一尺离地，

送行二步与人齐，五尺人高曾记;

仕女佳人争蹴，终朝笑语欢嬉，

良工高士素好奇，算出索长有几？

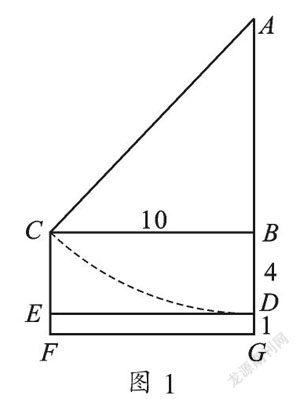
【分析】诗的意思告诉我们，当秋千静止在地上时，秋千的踏板离地的距离为1尺，将秋千的踏板往前推两步（这里是每一步合五尺）即10尺，秋千的踏板与人一样高，这个人的身高为5尺，当然这个秋千的绳索是呈直线状态，现在问这个秋千的绳索有多长？要解决这个问题，需要转化成图形语言.如图1所示，假设AD为静止时绳索的长度，DG=1，CF=5，BC=10，求AD的长度.

解：设AC为x，则AC=AD=x，

∵CF=BG=5，DG=1，

∴BD=BG-DG=5-1=4.

则AB=AD-BD=x-4.

∵在直角三角形ABC中，AC2=AB2+BC2，

∴x2=（x-4）2+102.

解这个方程，得x=14.5.

答：这个秋千的绳索的长度为14.5尺.

【点评】本题考查的是勾股定理在生活中的应用，充分挖掘题目中隐含信息是解决问题的关键.而在本题的解决过程中，把文字转化成图像也是解决问题的关键之一，这样最后才能达到数形结合.

二、 现代生活中勾股定理的应用

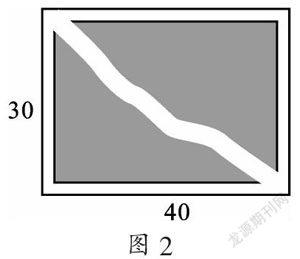
例2   老师的烦恼

最近学校一块长约40米、宽约30米的长方形草坪（图2），被几个不自觉的学生沿对角线踏出了一条斜“路”.请问同学们：

（1） 他们知道走斜“路”比正路少走几步路？

（2） 他们这样做，值得吗？

【分析】利用勾股定理求被学生走“白”的路线，然后与实际要求的路线进行比较.

（1） ∵402+302=2500=502，

∴斜路长50米，比正路少走40+30-50=20（米）.

（2） 践踏绿地，不爱护环境，我们要坚决制止.

【点评】本题考查同学们对勾股定理的应用，学生在审题和解决问题时能产生保护环境的意识.

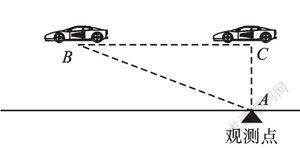
例3   “中华人民共和国道路交通管理条例”规定：小汽车在城市道路上的行驶速度不得超过70千米/时.如图4一辆小汽车在一条城市街道上直线行驶，某一时刻刚好行驶到路对面车速检测仪A正前方30米处，过了2秒钟后，测得小汽车位置B与车速检测仪A之间的距离为50米，问：这辆小汽车超速了吗？

【点评】由题意可知，△ABC为直角三角形，且AB是斜边，已知AB，AC根据勾股定理可以求出BC的长度，根据BC的长度和时间可以求出小汽车在BC路程中的速度.若速度大于70千米/时，则小汽车超速;若速度小于70千米/时，则小汽车没有超速.

解：在Rt△ABC中，AB2=AC2+BC2，

∵AB=50，AC=30.

∴BC=40米=0.04千米.

（千米/时）.

故该小汽车超速.

答：该小汽车超速了，平均速度大于70千米/时.

【点评】本题考查了勾股定理在实际生活中的应用，本题中正确地求出BC的长度，并计算小汽车的行驶速度是解题的关键.

古人在生活中发现了勾股定理，同时也把它应用在工程技术、测量中.有人还设想把勾股定理的图形与内容作为与外星人交流的“语言”.同学们，我们只要做一个生活的有心人，就会发现生活中处处都是数学.

（作者单位：江苏省常州市武进区湖塘实验中学）