衍射增强成像中余弦曲线拟合方法的噪声分析

鲍 园 王 研 朱佩平 吴自玉

1（中国科学技术大学 国家同步辐射实验室 合肥 230029）

2（中国科学院高能物理研究所 北京 100049）

衍射增强成像中余弦曲线拟合方法的噪声分析

鲍 园1,2王 研2朱佩平1,2吴自玉1,2

1（中国科学技术大学 国家同步辐射实验室 合肥 230029）

2（中国科学院高能物理研究所 北京 100049）

衍射增强成像是一种功能强大的相位衬度成像技术，其信息分离研究一直都是研究热点。提出了一种简便的信息分离方法——余弦曲线拟合法(Cosine Fitting Radiography, CFR)，该方法具有简便、样品所受辐射剂量低等优点。利用同步辐射实验和蒙特卡罗仿真方法，从角度信号成像模型出发解释了此方法，同时从噪声传递角度分析了该方法的性能和给出定量的评价指标，建立了衍射增强成像和光栅微分干涉成像之间更直观的联系。对理解衍射增强成像系统的噪声行为和提高信噪比具有一定的参考意义。

衍射增强成像，噪声分析，余弦曲线拟合，蒙特卡罗仿真

衍射增强成像(Diffraction Enhanced Imaging, DEI)，也叫基于分析晶体的成像方法(Analyzerbased Imaging, ABI)，可以对主要由碳、氢、氧等轻元素构成的软组织成像，同时获得吸收、折射和超小角散射信息。这种成像方法最初由Forster[1]在1980年提出，但在最近十几年才成为相衬成像领域的研究热点。衍射增强成像这个术语是由Chapman[2]在1997年引入，他将摇摆曲线线性近似，由两个半腰像，提取出样品的吸收像和折射像。随后，DEI的发展主要沿着两个方向进行：(1) 将摇摆曲线认为是角度信号响应函数，探测器接收的像就可以表达成样品角度函数和本征摇摆曲线的卷积形式；(2) 基于全波检波法，对比加入样品前后的摇摆曲线，分别计算其零阶、一阶、二阶矩，得到相应的吸收、折射和散射信息。Chapman的方法属于前者，高斯拟合法[3]以及Oltulu[4]、Wernick[5]的方法属于后者。

Chapman的方法采用线性近似，摇摆曲线在两个腰位处的二阶矩均为零，因此不能提取散射信息。为弥补这个缺点，Wernick等[5]提出多图法(Multiple-image Radiography, MIR)，利用辐射输运理论(Radiative Transport Theory)[6]建模X射线光场传播，证明了多图法可以真实地分离和提纯物体的吸收、折射和散射信息，并且对大摇摆角处由散射引起的图像退化有免疫作用。Rigon等[7-8]提出了一个可以替代多图法的方法，利用三张图提取三种信息，但是存在一些限制。胡春红等[3]提出用高斯曲线近似摇摆曲线，但该方法需要较多的图像采集次数。我们课题组根据Chapman的思路，将摇摆曲线视为角度信号响应函数，并采用余弦函数拟合(Cosine Fitting Radiography, CFR)[9]本征摇摆曲线，该方法只需三张图就可以获得能够与MIR相比较的结果。

DEI不仅为放射线照相术引入了折射像和散射像，而且触发了其他相衬成像方法的发展。尤其难能可贵的是，作为一个经典模型，它的结论可以扩展到所有基于准直器-分析器模型的成像方法中。虽然DEI是一种功能强大的相位衬度成像技术，但是仍然有很多问题亟待解决，比如与这个方法有关的定量性能分析，Brankov等[10]就分析了Chapman法的噪声特性。与此同时，基于光栅干涉成像的噪声分析也有大量工作[11-16]报道，Revol[11]发展了光栅微分干涉成像(Grating-based Phase Contrast Imaging, GDPCI)中随机误差的定量描述，Weber[14]引入矩阵形式的最小二乘方算法，同时计算吸收、折射、散射各自的方差以及它们之间的协方差。考虑到衍射增强成像和光栅干涉成像有很多相似之处，比如：它们都描述物体的折射角，即相位的一阶导数；散射像均来源于物体引起的可见度衰减；而且噪声模型相近，因此我们可以借鉴光栅干涉成像中的思想，转而分析衍射增强成像的噪声特性。本文从角度信号响应成像模型出发，全面分析了DEI中三种信息的噪声特性，证明了我们提出的方法的正确性，为提高成像系统的灵敏度提供了定量的依据，同时也建立了DEI和GDPCI之间更直观的联系。

1 余弦曲线拟合方法的基本原理

衍射增强成像原理如图1所示。

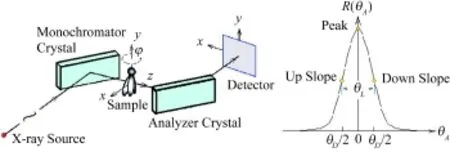
图1 衍射增强成像装置及其摇摆曲线Fig.1 Experimental set up for diffraction enhanced imaging and its rocking curve.

余弦曲线拟合方法的思路是：将角度信号响应函数视为余弦曲线，并用其拟合本征摇摆曲线：

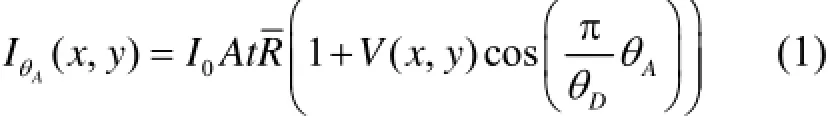
式中，IθA为探测器每个像素上接收到的光子数；I0为入射光平均强度（光通量）；A为探测器面积；t为采集一幅图时样品的曝光时间；表示余弦函数在一个周期内的平均值；表示本征摇摆曲线的等效可见度；),(yxV为样品摇摆曲线的可见度。为保证拟合结果的唯一性，只用峰位和腰位来拟合，效果如图2所示。图2中，上坡位(Up Load)和下坡位(Down Load)分别对应摇摆曲线两个半腰位置，峰位(Peak)对应摇摆曲线最大值。

图2 余弦函数拟合效果Fig.2 Fit of the intrinsic RC by the cosine function.

将样品放置在两块晶体的光路中，物体对光线的偏折等价于分析晶体的偏转：

式中，(,)V x y为样品摇摆曲线的等效可见度；0V为无样品时的可见度。可见度从0V变为(,)V x y的退化可看作是摇摆曲线对于散射信号的响应，其关系为：

2 噪声特性分析

我们考虑两种主要的噪声源，分别是光源光子数的波动和分析晶体的位置偏差。由此引起的总的误差可表示为各自误差之和：

2.1光源光子数的波动

由于光子数的波动，最终提取的吸收系数、折射角以及散射方差也会围绕其理论值波动。不失一般性，我们假设光源光子数波动符合泊松分布，运用误差传递理论[17]，计算这三种信息各自的方差：

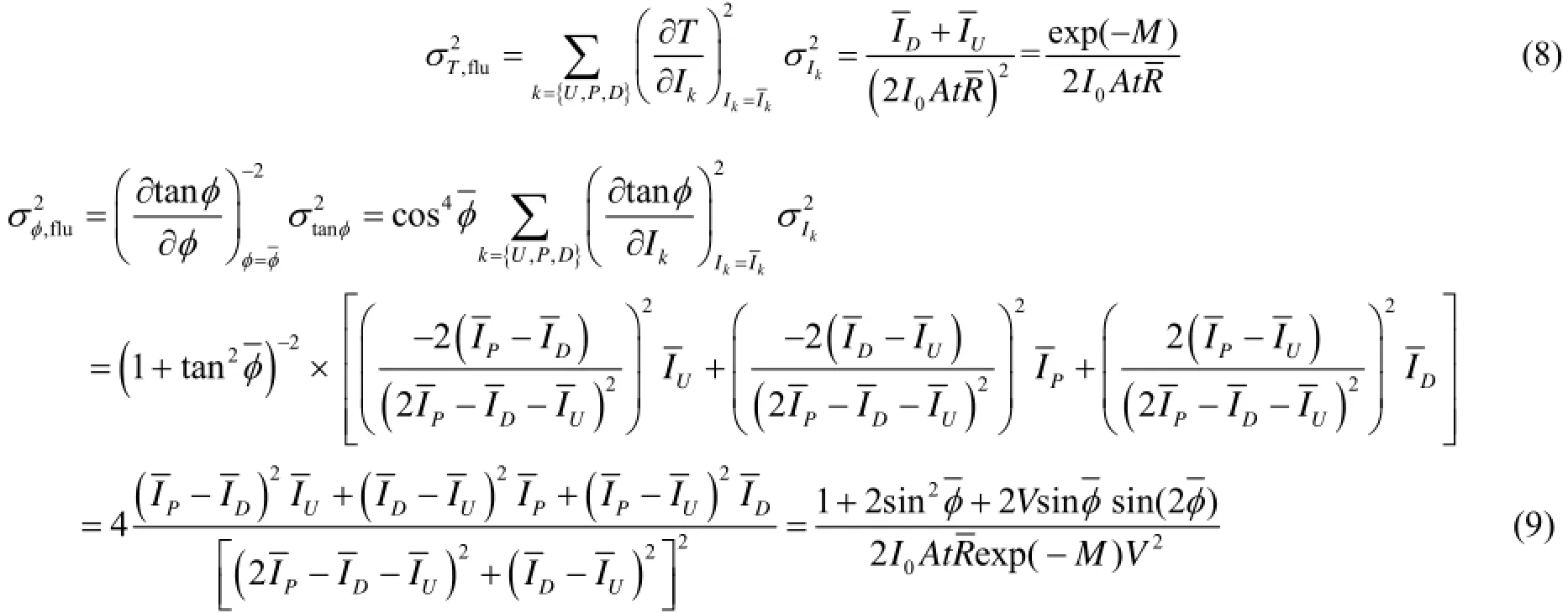
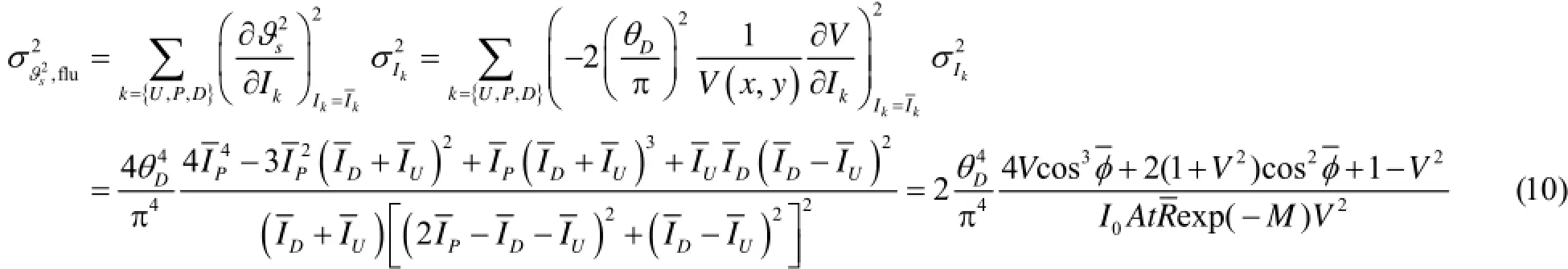
从式(8)-(10)可以看出，折射像和散射像的噪声受接收到的光子数、样品的吸收以及摇摆曲线的等效可见度影响，而吸收像的噪声只与接收到的光子数有关。

如果折射角足够小，式(9)、(10)可分别简化为：

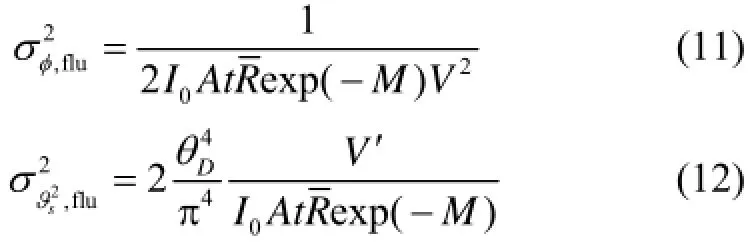
其中，V′=1+4/V+3/V2。

2.2分析晶体的位置偏差

DEI中采集图像需要将分析晶体放置在不同的角度位置，然而由于机械误差和抖动，实际的位置是围绕理想位置分布的。这些位置偏差最终会导致提取信息的误差。假设分析晶体在上坡位、峰位和下坡位的方向位置偏差分别为UθΔ、PθΔ和DθΔ，同样运用误差传递理论，可以得到：

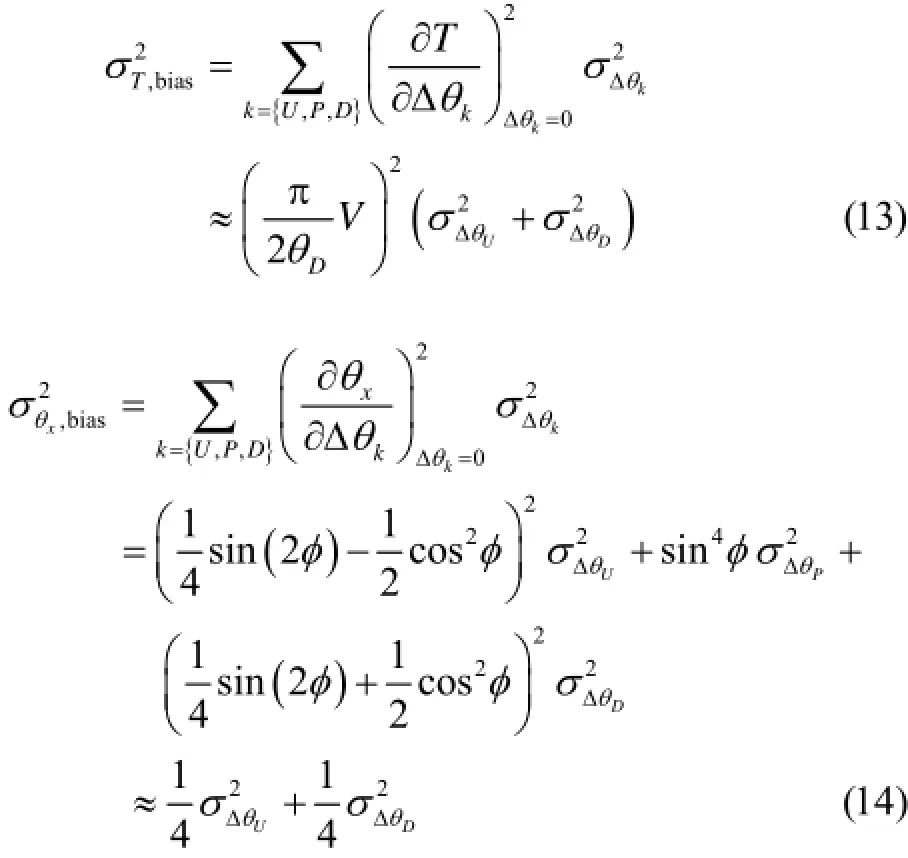
可以发现，上坡位和下坡位的偏差是等权重的，且峰位的偏差可以忽略。因此，采样时降低了分析晶体在峰位处的位置精度要求。

信噪比定义为信号变化系数的倒数，用信号的平均值与标准方差之比表示。最终，可以得到吸收、折射和散射信息的信噪比为：

其中，Itotal=I0At是入射光子数。

3 仿真和实验

实验在北京同步辐射光源4W1A形貌成像站的微分相衬成像装置上进行。样品是圆柱型PMMA和不同层数的滤纸，PMMA是主要的折射材料，滤纸是主要的散射材料。两块Si(111)晶体分别用作单色器和分析器。单色器晶体选择的能量为15keV，分析晶体的转动精度为0.1 mrad，曝光时间从40ms以5ms为步长增加到100ms，用像素为7.4μm×7.4μm的探测器检测光子信号。与此同时，运用基于Geant4[18-19]的蒙特卡罗仿真，设置与实验一致的条件，模拟粒子与材料的真实作用过程。Geant4是当前模拟粒子输运过程的主流开源工具，可以很好地描述X射线的粒子性。基于斯涅耳定律引入折射效应，使Geant4具有相衬成像能力[20]。构建的样品模型如图3所示，圆柱是直径3mm的PMMA，滤纸分为7个不同的高度代表不同的散射能力，紧贴放置于圆柱体之后。

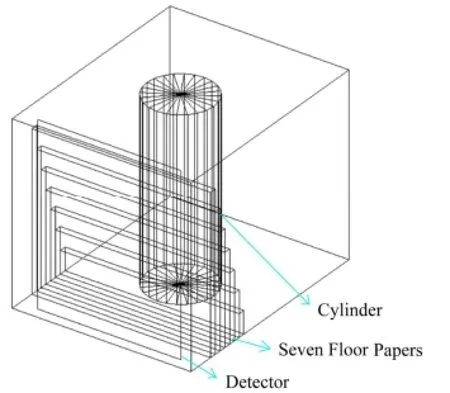
图3 蒙特卡罗仿真样品模型Fig.3 Sample construction in Monte Carlo simulations.

按照CFR方法，得到的仿真和实验结果如图4。

可以发现，随着纸张厚度增加，吸收和散射逐渐增强，但折射像没有受到明显影响。分别计算图4方框内部以及沿虚线的噪声标准差进行比较，将折射像和散射像的噪声偏差分别以曝光时间和等效可见度为因变量进行关联并拟合，结果见图5。

图4 实验提取的吸收(a)、折射(b)和散射(c)方差像以及蒙特卡罗模拟得到的对应结果(d-f)Fig.4Absorption (a), refraction (b) and scattering (c) images extracted from experimental data, while (d-f) are those of Monte Carlo simulations.

图5 折射角的标准差和散射方差的标准差随时间和摇摆曲线等效可见度的变化关系(a)和(b)表示折射角的结果，(c)和(d)表示散射方差像的结果Fig.5 Standard deviations σθxand σplotted vs. the exposure time and the equivalent visibility of the RC. (a) and (b) show the results of the refraction-angle images, (c) and (d) show the results of scattering images

根据罗斯判据[21]，信噪比至少达到5的时候，才有可能100%的区分图像细节。基于仿真结果，用每个像素的平均光子数描述探测器平面的平均强度，计算出圆柱边界处的信噪比随平均强度变化的关系如图6所示。

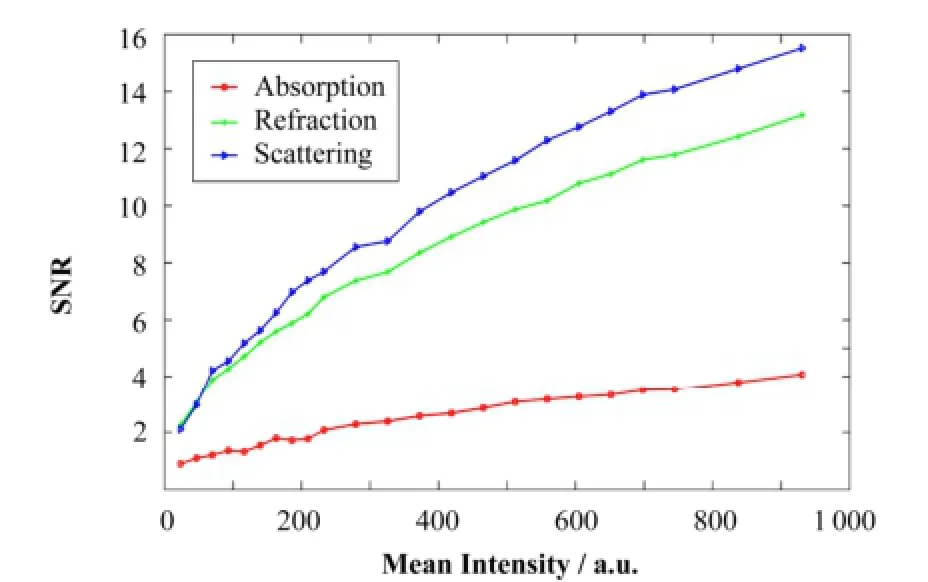
图6 吸收、折射和散射像在边界处的信噪比随平均光子数的变化趋势Fig.6 SNRs at the boundary of the sample vs. the mean intensity in the detector plane.

模拟结果显示，信噪比随探测器平面的平均强度而提高。相比吸收像，即使探测器平面的光子数仅为100，折射像和散射像的在样品边界处信噪比也是足够的。体现了折射像和散射像在表达由轻元素组成的物质的边界时具有优势。

4 讨论

文中折射定义为相邻面积元之间的密度不均匀引起的相干散射，其对应的物理图像是单一方向光线入射在样品上，虽然相邻面积元的出射光线方向有可能不同，但是每个面积元的出射光线只有一个方向；小角散射定义为面积元内部的密度不均匀引起的相干散射，其对应的物理图像是单一方向光线入射在一个面积元上，出射光线有多个方向。由此可知，在衍射增强成像中折射和小角散射的区分不是绝对的而是相对的，两者在一定条件下可以相互转化。当成像分辨率降低时，样品的面积元增大，一部分折射转化为小角散射；而当成像分辨率提高时，样品面积元减小，一部分小角散射转化为折射。

基于CFR计算出DEI的噪声特性，与之前用最大似然估计(Maximum Likelihood Estimation, MLE)[10]所得的结果一致。值得注意的是，这个结果也类似于用相步进方法[14]或者正反像投影方法[22]在光栅微分相衬成像中的结论。因为这两种相衬成像方法的共性在于提取的相衬信息均是折射角。关于吸收、折射和散射方差这三种信息之间的协方差可以通过协方差矩阵来计算，衍射增强CT系统中的噪声特性将作为下一步的工作进行开展。此外，文中所采用的噪声模型考虑了光源的光子数波动和分析晶体的位置偏差。实际上，其他因素诸如暗电流噪声、晶体缺陷和热不稳定性也在影响结果，但他们都太小以致可以忽略。

余弦曲线拟合方法还有一个优势：可以用三块分析晶体，分别定位在角度信号响应曲线的上坡腰位、峰位和下坡腰位，同步辐射单色X射线光束一次扫描样品，可以同时拍摄到上坡腰位像、峰位像和下坡腰位像，从而利用余弦曲线拟合方法进行信息分离。这个设想为医学和生物研究者带来了新的机遇，有望在降低辐射损伤和提高成像效率方面取得进步。

5 结语

基于角度信号成像理论，分析了余弦拟合算法的噪声特性。通过蒙特卡罗模拟和实验验证了此算法和噪声结果的正确性。随着通量的增加、等效可见度的提高，噪声引起的图像退化将迅速减小。在样品边界处，折射角信号和散射方差信号的信噪比高于吸收系数信号，探测器平面的平均光子数只要达到100，便可满足罗斯判据。本文的噪声分析工作建立了DEI和GDPCI之间更直观的联系，并且广泛适用于角度信号成像模型下的各种噪声测量和分析。

1 Forster E, Goetz K, Zaumseil P. Double crystal diffractometry for the characterization of targets for laser fusion experiments[J]. Crystal Research and Technology, 1980, 15(8): 937-945. DOI: 10.1002/crat.19800150812

2 Chapman D, Thomlinson W, Johnston R, et al. Diffraction enhanced X-ray imaging[J]. Physics in Medicine and Biology, 1997, 42(11): 2015. DOI: 10.1088/0031-9155/ 42/11/001

3 Hu C, Zhang L, Li H, et al. Comparison of refraction information extraction methods in diffraction enhanced imaging[J]. Optics Express, 2008, 16(21): 16704-16710. DOI: 10.1364/OE.16.016704

4 Oltulu O. A unified approach to X-ray absorptionrefraction-extinction contrast with diffraction-enhanced imaging[D]. Illinois Institute of Technology, UMI Number: 3087854, 2003

5 Wernick M N, Wirjadi O, Chapman D, et al. Multiple-image radiography[J]. Physics in Medicine and Biology, 2003, 48(23): 3875-3895. DOI: 10.1088/ 0031-9155/48/23/006

6 Khelashvili G, Brankov J G, Chapman D, et al. A physical model of multiple-image radiography[J]. Physics in Medicine and Biology, 2006, 51(2): 221-236. DOI: 10.1088/0031-9155/51/2/003

7 Rigon L, Besch H J, Arfelli F, et al. A new DEI algorithm capable of investigating sub-pixel structures[J]. Journal of Physics D: Applied Physics, 2003, 36(10A): 107-112. DOI: 10.1088/0022-3727/36/10A/322

8 Rigon L, Arfelli F, Menk R H. Three-image diffraction enhanced imaging algorithm to extract absorption, refraction, and ultrasmall-angle scattering[J]. Applied Physics Letters, 2007, 90(11): 114102. DOI: 10.1063/ 1.2713147

9 赵雪娇, 张凯, 洪友丽, 等. 衍射增强成像提取多种信息的简便方法研究[J]. 物理学报, 2013, 62(12): 124202. DOI: 10.7498/aps.62.124202 ZHAO Xuejiao, ZHANG Kai, HONG Youli, et al. A simple method of extracting multiple-information with diffraction enhanced imaging[J]. Acta Physica Sinica, 2013, 62(12): 124202. DOI: 10.7498/aps.62.124202

10 Brankov J G, Iz-Herranz S A, Wernick M N. Noise analysis for diffraction enhanced imaging[A]. 2004 2ndIEEE International Symposium on Biomedical Imaging: Macro to Nano[C]. New York: IEEE, 2004, Vols 1 and 2: 1428-1431

11 Revol V, Kottler C, Kaufmann R, et al. Noise analysis of grating-based X-ray differential phase contrast imaging[J]. Review of Scientific Instruments, 2010, 81(7): 073709. DOI: 10.1063/1.3465334

12 Tang X Y, Yang Y, Tang S J. Characterization of imaging performance in differential phase contrast CT compared with the conventional CT: spectrum of noise equivalent quanta NEQ(k)[J]. Medical Physics, 2012, 39(7): 4467-4482. DOI: 10.1118/1.4730287

13 Diemoz P, Bravin A, Langer M, et al. Analytical and experimental determination of signal-to-noise ratio and figure of merit in three phase-contrast imaging techniques[J]. Optics Express, 2012, 20(25): 27670-90. DOI: 10.1364/OE.20.027670

14 Weber T, Bartl P, Durst J, et al. Measurements and simulations analysing the noise behaviour of grating-based X-ray phase-contrast imaging[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2010, 648: S273-S5. DOI: 10.1016/ j.nima.2010.11.060

15 Rizzi J, Mercere P, Idir M, et al. X-ray phase contrast imaging and noise evaluation using a single phase grating interferometer[J]. Optics Express, 2013, 21(14): 17340-17351. DOI: 10.1364/OE.21.017340

16 Li K, Bevins N, Zambelli J, et al. Fundamental relationship between the noise properties of grating-based differential phase contrast CT and absorption CT: theoretical framework using a cascaded system model and experimental validation[J]. Medical Physics, 2013, 40(2): 021908-021922. DOI: 10.1118/1.4788647

17 Chen G H, Zambelli J, Li K, et al. Scaling law for noise variance and spatial resolution in differential phasecontrast computed tomography[J]. Medical Physics, 2011,38: 584-588. DOI: 10.1118/1.3533718

18 Agostinelli S, Allison J, Amako K A, et al. GEANT4-a simulation toolkit[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2003,506(3): 250-303. DOI: 10.1016/S0168-9002(03)01368-8

19 Allison J, Amako K, Apostolakis J, et al. Geant4 developments and applications[J]. IEEE Transactions on Nuclear Science, 2006,53(1): 270-278. DOI: 10.1109/ TNS.2006.869826

20 Wang Z, Huang Z, Zhang L, et al. Implement X-ray refraction effect in Geant4 for phase contrast imaging[A]. Bo Y. 2009 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC 2009)[C]. Piscataway: IEEE, 2009: 2395-2398. DOI: 10.1109/ NSSMIC.2009.5402180

21 Bushberg J T, Boone J M. The essential physics of medical imaging[M]. Philadelphia, Pa: Lippincott Williams & Wilkins, 2012: 86-92. DOI: 10.1148/radiol. 14144045

22 Zhu P, Zhang K, Wang Z, et al. Low-dose, simple, and fast grating-based X-ray phase-contrast imaging[J]. Proceedings of the National Academy of Sciences, 2010,107(31): 13576-13581. DOI: 10.1073/pnas.1003198107

Noise analysis of cosine fitting radiography for diffraction enhanced imaging

BAO Yuan1,2WANG Yan2ZHU Peiping1,2WU Ziyu1,2

1(National Synchrotron Radiation Laboratory,University of Science and Technology of China,Hefei 230029,China)
2(Institute of High Energy Physics,Chinese Academy of Sciences,Beijing 100049,China)

Background:Diffraction enhanced imaging (DEI) is a powerful phase contrast imaging technique.Purpose:This study aims to investigate the noise properties of a new simple cosine fitting radiography for DEI based on the angular signal response imaging prototype.Methods:The rocking curve can be treated as a angular signal response and a simple multi-information retrieval algorithm based on the cosine function fitting. A comprehensive analysis of noise properties in DEI, based on a noise model including the fluctuation of the photon source, and a bias of the analyzer crystal are also given. The validations have been performed with Monte Carlo simulations based on the Geant4 toolkit combined with the refractive process of X-ray and synchrotron radiation experimental data.Results:The cosine fitting radiography (CFR) has been verified by Monte Carlo simulations and experimental data which are in good agreement with each other. The noise penalty is drastically reduced with high photon flux, high visibility and high angular precision.Conclusions:Based on the angular signal response function prototype, we analyze and calculate the noise properties of DEI. In addition, the analytical method can build a strong connection between DEI and grating-based phase contrast imaging (GDPCI) and widely suitable for all kinds of measurement noises in angular signal response imaging prototype. The analysis is useful to understand the noise characteristics of DEI images and improve the signal-noise-ratio of the extracted information for biomedical imaging and material science.

Diffraction enhanced imaging, Noise analysis, Cosine fitting radiography, Monte Carlo simulations

TL99

10.11889/j.0253-3219.2015.hjs.38.090101

基础研究国家重点项目(No.2012CB825801)、创新研究团体基金项目(No.11321503)、国家自然科学基金(No.11205157、No. 11205189、No.11375225、No.U1332109)资助

鲍园，男，1990年出生，2011年毕业于安徽大学，现为硕士研究生

朱佩平，E-mail: zhupp@ihep.ac.cn；吴自玉，E-mail: wuzy@ustc.edu.cn

2014-08-28，

2015-03-10

CLCTL99