狼和鹿生态系统数学模型的稳定性分析

刘玉丽，姜玉秋

(吉林师范大学数学学院，吉林长春130103)

1 建立模型

在同一理想的小环境D中研究捕食者和食饵种群，两种群变化的Volterra模型［1］.

其中x(t)和y(t)分别表示t时刻在小环境D中食饵和捕食者的数量，r1和r2分别表示食饵和捕食者的内禀增长率，a和d分别表示食饵和捕食者的密度制约项，b表示单位时间内捕食者吃掉食饵的数量，c表示当存在食饵种群时，被捕食者吃掉的食饵将被转化成对捕食者有利的能量分别表示田鼠和蛇在这个小环境中的相对增长率［2］.

2 系统分析

在美国亚里桑那州北部凯巴伯森林地区的一个理想小环境中有两个发生捕获系统的种群——狼和鹿.利用同一种生存资源，假设这个小环境里的狼和鹿的生长都处于健康状态.考虑到生物学意义，本文仅在区域D={(x，y)|x≥0，y≥0}［3］上研究系统(1.1).容易得到，系统(1.1)有 O(0，0)E(x*，y*)四个平衡点存在，其中x*＞0，y*＞0.在区域D上将系统(1.1)变形为

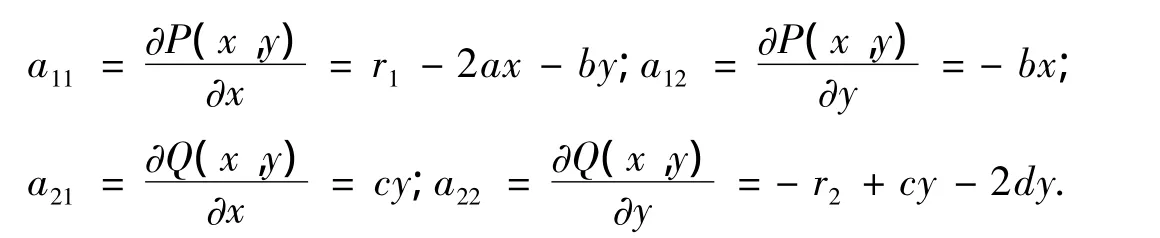
令Δ =a11a22－a12a21，δ=－(a11+a22).

定理2.1 系统(1.1)在区域D内无闭轨［4］.

定理2.2系统(1.1)的平衡点O(0，0)为鞍点.

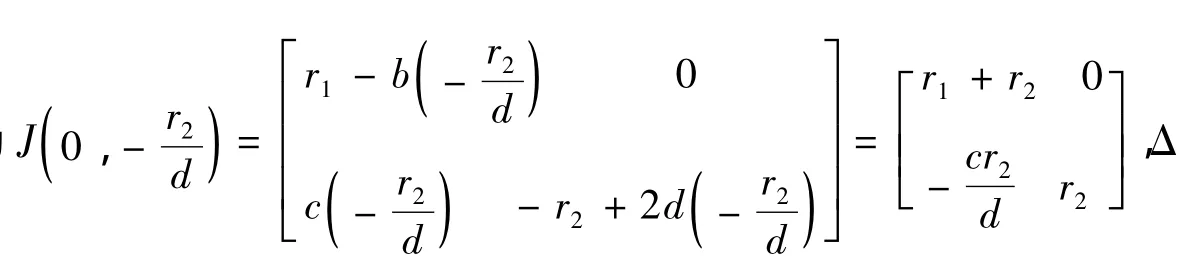
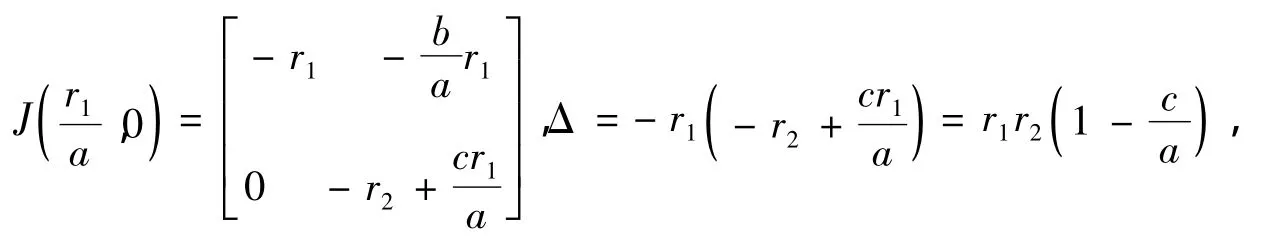
定理2.5系统(1.1)存在唯一的正平衡点E(x*，y*)是局部稳定的.

证明 首先证明正平衡点E(x*，y*)的存在唯一性［5］.考虑代数方程组F1(x，y)=0;F2(x，y)=0，由第二个方程得，代入第一个方程得=0，引进辅助函数f(y)＜0.由零点定理知，存在，使得f(y*)=0.又因为f'(y)，即f(y)是关于y的严格单调减函数，故y*在是唯一的，由x=可得相应的x*.所以a＞c＞r2＞0时系统(1.1)有唯一的正平衡点E(x*，y*).

下面证明 E(x*，y*)是局部稳定［7］.

正平衡点E(x*，y*)的Jacobi矩阵

Δ=(r1－2ax*－by*)(－r2+cx*－2dy*)+bcx*y*，

δ=(r1－2ax*－by*－r2+cx*－2dy*)=r2－r1+x*(2a－c)+y*(b+2d).

当r2＞r1，2a＞c时，Δ ＞0，δ＞0.可知E(x*，y*)是局部渐进稳定的.

由定理2.1至定理2.5，易证得下面的结论.

定理2.6 a＞c＞r2＞0，r2＞r1时，系统(1.1)的正平衡点E(x*，y*)是全局渐进稳定的.

利用Matlab程序模拟出系统(1.1)在平衡点D(x*，y*)附近过不同初值点的轨线，如图1所示.

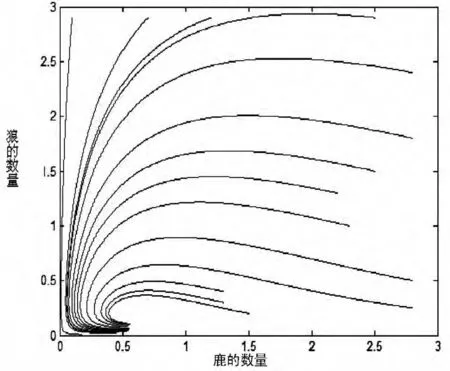
图1 狼与鹿两种群数量变化图

3 生物学意义

综上，对系统(1.1)进行了稳定性讨论与分析，得到了适合捕食者与食饵生存的数量D(x*，y*).因想要有效地保护鹿而消灭鹿的天敌狼等野兽，致使鹿群的数量得到了自由的增长，当其数量增长到一定程度时，森林中的绿色植被就遭到破坏，导致鹿大量死亡，这就违背了人们当初的意愿［6］.在自然的状态下，可以利用此模型的平衡点D(x*，y*)进行人为干预，当鹿种群繁殖数量增大时，引入狼来控制鹿的增长速度，使两种群的数量在各自的环境容纳量下达到各自的平衡点x*和y*.这样，森林也就不会被鹿群糟蹋得面目全非，也有效地控制了疾病对鹿群的威胁，从而实现了保护森林生态系统稳定的目的［8］.

［1］马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京:科学出版社，2001.

［2］尚玉昌.普通生态学［M］.北京:北京大学出版社，2002.

［3］姜启源，谢金星，叶俊.数学模型［M］.北京:高等教育出版社，2003.

［4］姜玉秋.Turchin－Batzli捕食者－食饵系统的定性分析［J］.东北师大学报:自然科学版，2006(4):17－21.

［5］Verhust F.Nonlinear Differential Equations and Dynamical Systems［M］.Berlin:Springer－ Verlag，1996.

［6］Perter Turchin，George O.Batzli.Availability of Food and the Population Dynamics of Arvicoline Rodents［J］.The Ecological Society of American，2001.

［7］柏灵，李晓月，杨帆.捕食－食饵系统的两种群同时捕获的最优化问题［J］.东北师大学报:自然科学版，2001，33(1):1－5.

［8］王顺庆，王万雄，徐海根.数学生态学稳定性理论与方法［M］.北京:科学出版社，2004.