基于熵理论的城市主－支路交汇处交通状态判别

刘 雪，杨 开，赵 鑫，杨兆升

(1.长春师范大学工程学院，吉林长春130032;2.吉林大学交通学院，长春吉林130022)

目前，道路的增长速度不能满足于汽车保有量的增长速度，因而当道路的交通量接近道路的最大通行能力时，道路交通系统便不能高效有序地运行，而是表现出某种程度的车流紊乱，从而导致车辆运行速度降低、拥堵加剧、延误增长等一系列交通问题。作为城市快速路的一部分，支路合理高效的通行变得尤为重要。道路交通系统与热力学系统有着明显的区别，但就其系统本身而言，又与热力学系统存在许多相似之处。鉴于此，本论文引入熵来描述道路交通系统的状态。

熵是系统的状态函数，因此道路交通系统的熵可以作为其运行状态的度量。其中熵值小，表明系统有序，即道路的服务水平高;反之熵值大，表明系统紊乱，道路的服务水平降低。

1 交通系统中流和力的确定

根据经典热力学理论，任何宏观系统的状态都可引用状态函数熵S来描述。对于任一宏观系统，普利高津将熵 ds的变化分解为两项之和［1－2］，即

或

其中，dis—— 熵产生，des—— 熵流，令 pi=，称pi为熵产生率。

熵产生可以用广义热力学力X和广义热力学流J来表示［3］。力是流产生的原因，广义力越大，引起的流就越大，不可逆变化也更迅猛。当开放系统处于线性非平衡区时，由于负熵流的流入，抑制了系统自身的熵产生，所以熵产生率随着时间的进行而减小。当系统达到定态时(即ds=dis+des=0)，pi取得最小值，此时力和流都不再随时间变化，这就是最小熵产生原理［4］。

平衡系统中小区域的熵产生可以描述为

非平衡系统中，如果同时存在多种不可逆过程，那么该系统的熵产生就与多种力和流有关。该系统的熵产生 ——δ可以描述为

其中，Jk—— 第 k种流，Xk——引起第k种流的力。

由局域平衡假设可知

其中，V——系统体系。

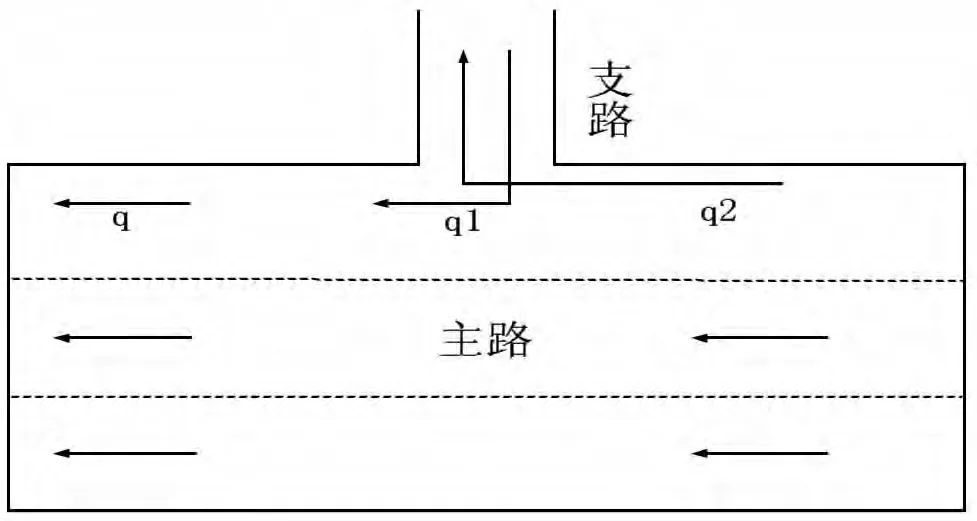
图1 主－支路交汇处交通流量变化图

根据流体力学中质量守恒定律及其连续方程可知，当从支路汇入主路的车辆数等于从主路驶入支路的车辆数时(图1)，满足。该式表明在此路段内汽车的数量是恒定的，即此时为平衡态;而当该路段的处于非平衡态时，通过最小熵原理可得

其中，q1——从支路进入主干道的交通量，q2——从主干道驶入支路的交通量。

设主路交通流的变化量为qn=q1－q2.

图2 主路交通流受力分析图

如图2所示，在主路某车道中任取一路段Δx，对其进行图中所示受力分析。记P0为已知状态的虚拟力，则该路段上的车辆数为kΔX，与之对应的虚拟力的合力增量为Δp;在不考虑粘性力［5］存在的条件下，由于路段车辆的进出对原主路产生干扰，故引入干扰力f。由动量定理可以推导出

其中，Δv—— 速度的增量，v0——初始状态的速度。

类比牛顿第二定律F=ma推出

其中，a——路段车辆的加速度。

其中，q——主路的交通量。

对(9)推导得该路段的交通压力方程为

交通压力P可以描述为:综合了驱使交通流向前运动的驱动力、路面及交通设施对交通流的阻力和支路对主干道的干扰力等因素的广义力。

2 交通系统熵产生模型及其状态判别熵模型的建立

将上述所求的广义力在本路段的增量和广义流在本路段的增量代入(3)中，并将所得结果对研究路段进行积分可以得到熵产生率Pi，即

或

以上两式即为两种状态(有干扰交通量和无干扰交通量)下的交通系统熵产生模型。

首先，选取某一时刻的交通状态为其初始状态，并由此确定其它状态的熵产生模型，得到以下模型

(14)即为改进后的交通系统熵产生模型。

经过上面的推导可以求得初始状态时系统熵值S，

(15)即为道路交通系统熵值模型。

在城市道路交通系统中，一方面希望道路熵值小，系统趋于稳定，道路服务水平高;另一方面又希望道路能有更大的通行能力，而不是单纯的熵值最小。这就要求找到一个基准态。

选定交通量最大时为基准态(v=vm，k=km)，此时熵值为Sm。当S＞Sm时，需要向系统中注入负熵流S。

负熵流的注入对交通系统的有序化具有推动作用，帮助系统趋向有序，又能使道路的通行能力达到最佳。此时路段的交通总熵为

即

(17)为注入负熵流之后的道路的交通总熵。

初始状态时，P0=0，qn=0，取v0=vf代入(15)式中，得到初始状态的交通熵模型

将基准态时的条件(v=vm，k=km)代入(18)式中，可推导出

其中，vm—— 临界速度—— 最佳密度

为了更简单、直观地描绘交通系统某时刻的状态，引入交通状态判别熵——sf，令

(20)为交通状态判别熵模型。

3 对交通熵模型的验证

本文以长春市临河街与威海路交汇处为例对模型进行验证，基础数据来源于5个工作日的晚高峰(4:30～6:00)交通量和速度调查。根据国内外研究惯例，以5分钟为标准时间间隔，顺次记为1，2，3，……共18组。调查数据整理如表1所示。

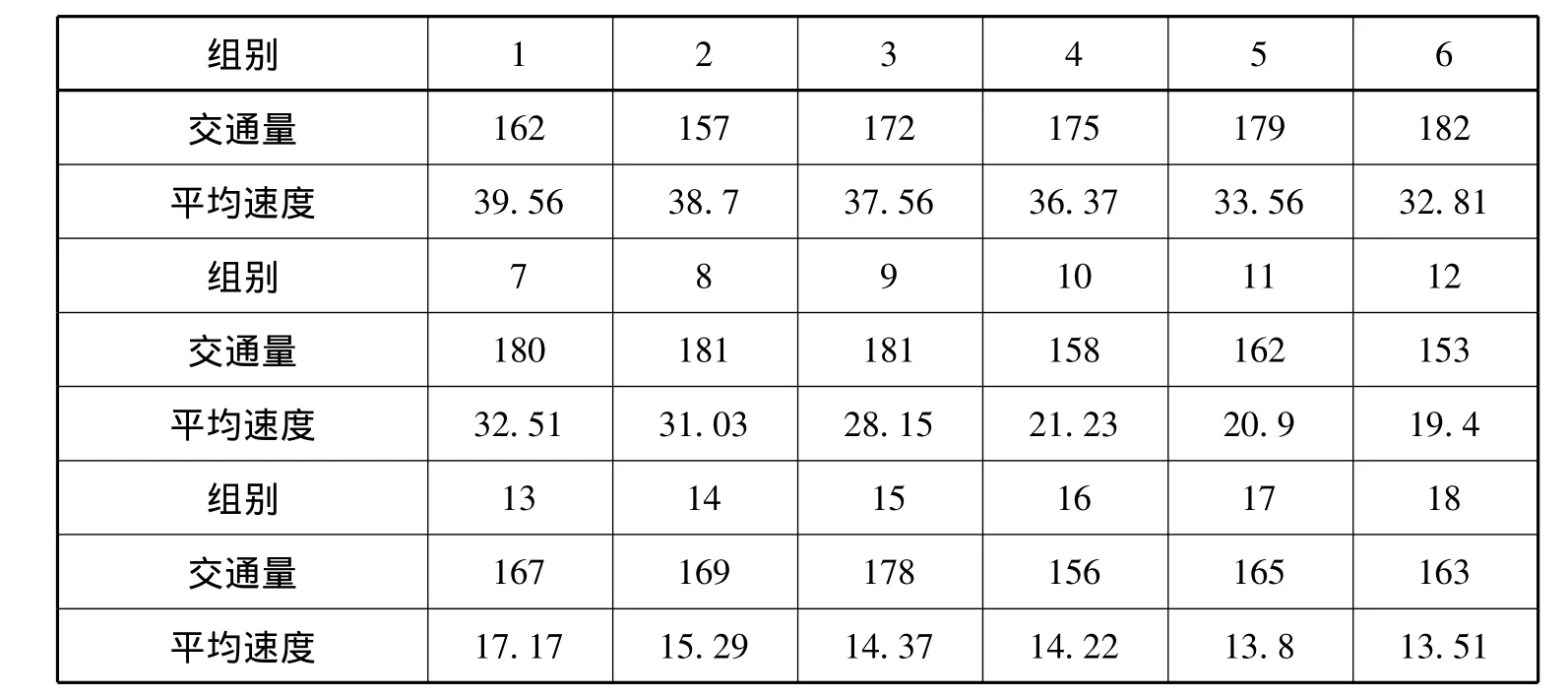
表1 晚高峰交通量与平均速度调查表(单位:交通量 veh·5min－1;平均速度 km·h－1)

由于在临河街与威海路交汇处限速40km·h－1，故vf=40km·h－1，vm=20km·h－1，通过查询《道路通行能力手册》可知，此时路段单车道最大通行能力为1050辆·h－1;根据Q=kv，可得Km=63 veh·h－1及k，运用公式(20)求得交通状态判别熵Sf值如表2所示。

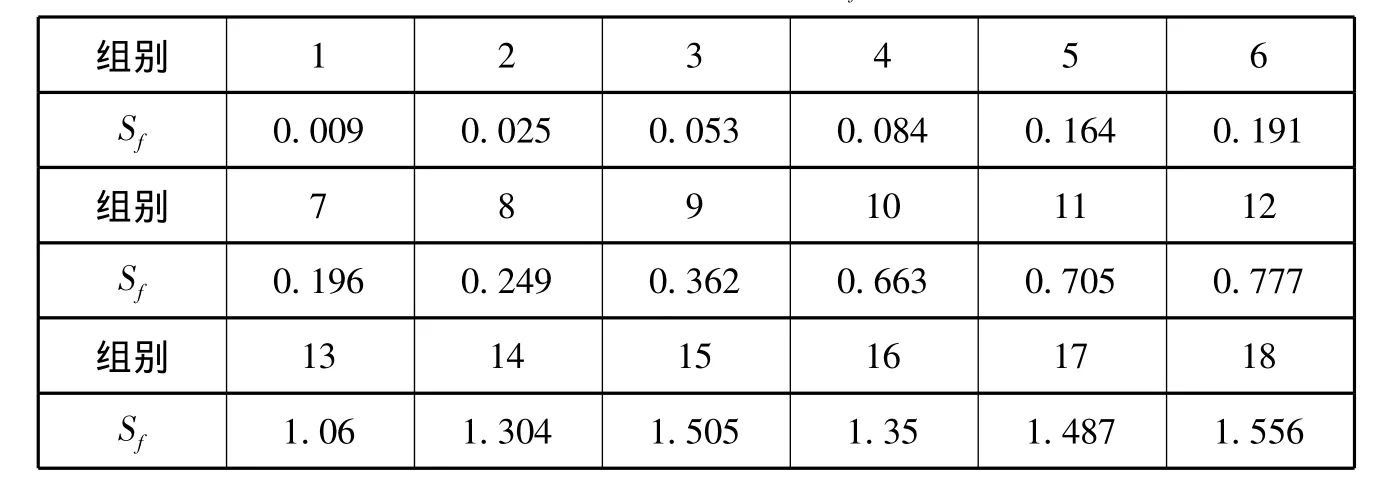
表2 交通状态判别熵Sf值表

运用MATLAB软件，对实测数据进行拟合得平均速度 －交通状态熵值关系图如图3所示。

对图3进行分析可知，拟合结果的残差R2=0.9979。因一般情况下R2＞0.95时，表示拟合结果可信，故图3所示的拟合效果较为理想。还可以明显看出，平均行车速度越大，交通状态熵越小;反之平均行车速度越小，交通状态熵越大。这与前面第一部分理论分析阶段的判别结果是一致的，间接证明了本文建立的交通状态熵模型是成立且有效的。

由以上研究可知，在主 －支路交汇或主 －辅路交汇处等有干扰交通的路段，可对其采取相应的管控措施以降低交通熵值(如在主路交通流分/合流处增设一条辅助车道，车辆先进入辅道后再汇入主路以减少分 /合流交通量对主路的影响)，从而提高道路的通行能力。

图3 平均速度－交通状态熵值关系图

4 结语

交通流熵值模型的建立为我们对道路交通系统状态的判别提供依据。通过对道路总熵模型注入负熵流的方式达到对道路交通系统状态进行调整的目的，从而提高道路的通行能力，为交通管理部门采取有效的管控措施提供了理论依据。

［1］邱洁.基于熵和流体力学的城市主干道的状态判别方法研究［D］.哈尔滨:东北林业大学，2010.

［2］王春蕾.基于热力学熵的城市快速路的交通状态判别方法研究［D］.哈尔滨:东北林业大学，2011.

［3］强添纲.基于交通噪声的交通量方法研究与实例分析［J］.森林工程，2009(2):70－72.

［4］沈维道，童钧耕.工程热力学［M］.北京:高等教育出版社，2007.

［5］薛郁.随机计及相对速度的交通流跟驰模型［J］.物理学报，2003(11):2750－2756.

［6］王炜，过秀成.交通工程学［M］.南京:东南大学出版社，2012.