基于Markowitz组合理论的风险控制分析

尹海英，张若丹

（1.吉林省科技金融研究中心，吉林 长春 130028；2.长春金融高等专科学校 金融系，吉林 长春 130028；3.中国财政经济出版社，北京 100142）

一、Markowitz组合理论对风险的分析

所谓的组合投资就是不要将鸡蛋放在同一个篮子里，而是把资金以一定的比例分散地投资于多种证券和资产，以减少所面临的投资风险。在投资实践中，投资者在自觉或不自觉地运用组合投资来降低风险，组合投资是证券投资的主要形式。Markowitz投资组合理论中关于组合投资优于单一资产投资，以及存在优势的条件和关键，都是通过数学公式的计算和推导得到的。对于多元化投资分散风险的分析，主要考虑资产的数目、资产间的关联度，以及资产的投资比率（即权重）。n种证券的组合投资中投资权重向量X=（x1，x2，…，xn），方差-协方差矩阵Σ=（σij）nn，则组合风险为：

其中，x1+x2+…+xn=1

Markowitz投资组合理论主要包括资产选择和均值-方差分析两部分内容。

（一）资产选择

对组合风险的公式进行数学推导，发现当n越大时，就越小；当n→∞时，组合风险无限地趋近于一个特定的值。这说明组合资产风险随着资产数目增多而减小；但仅靠增加资产数目降低风险时，却不能规避所有的风险，资产多元化不能规避掉的这部分风险，本文不作讨论。而且，通过深入研究和分析发现，随着资产数目增加，资产组合风险减少程度越来越小，呈现边际递减（如图1所示）。所以，投资者受到时间、精力和资金等限制，组合资产的数量并不是多多益善。相关研究表明，资产数目在10～20之间可以充分分散风险。

图1 资产数目对资产组合风险的影响

Markowitz组合理论用协方差和相关系数描述资产间的关联程度，协方差仅能描述两个资产收益率变动相互作用的方向，相关系数不仅能描述两个资产收益率变动相互作用的方向，还能描述两个资产收益率变动相互作用的程度。相关系数和协方差的关系为：

可以将其带入公式（1）中，发现相关系数对资产组合风险有直接的影响。相关系数的取值范围是ρ∈［－1，1］，相关系数越小，表明资产间的相关程度越小，降低风险的程度越大，资产组合的风险也就越小。如图1中的a和b所示。

（二）Markowitz均值-方差分析

资产权重对组合结果的影响与资产数目和资产间相关系数的影响不一样，后两个因素的改变仅仅影响资产组合风险的大小，而组合中资产权重的改变不仅影响组合风险的大小，而且影响组合资产收益E（Rp）=x1R1+x2R2+…+xn Rn的高低。所以，当投资者即使是通过资产选择原则、资产间的相关系数选对了证券，并且将资产数目确定在最佳的范围之内，当权重改变时，投资资产组合中可能会出现收益低、风险大的投资组合（如图2所示）。Markowitz投资组合理论的核心问题是：在投资决策中构建出同等风险（用方差或标准差描述）水平下、选择收益（用数学均值描述）最大，或是同等收益水平下、风险最小的投资组合，也就是运用均值-方差模型来构造有效的投资组合。Markowitz均值-方差模型分为两类：不包含无风险资产的Markowitz均值-方差模型和包含无风险资产的Markowitz均值-方差模型。

1.不包含无风险资产的Markowitz均值-方差模型

（1）模型内容

模型Ⅰ图示如图2。图中虚线和实线共同构成了组合投资的均值-方差界面，在界面上，相同的收益水平风险最小。界面的虚线部分随着收益的减小，风险却在加大，是投资者不愿意选择的无效投资组合；实线部分随着收益的增加，风险也在增加，称为有效边界。投资者的投资选择就在有效边界上。

图2 不包含无风险资产的有效组合

图3 包含无风险资产的有效组合

（2）模型求解

求解该模型采用Laganerge乘子法，首先构建Laganerge函数

其次，对公式（2）对xi一阶求导，则资产组合中n个资产的权重xi与两个Laganerge乘子λ、μ满足方程组Ⅰ

从而可得到xi的值，最终构造出一个有效投资组合。

2.包含无风险资产的Markowitz均值-方差模型

（1）模型内容

模型Ⅱ中的（σc，Rc）表示包含风险资产和无风险资产的组合——完全资产组合的风险和收益。模型Ⅱ图示如图3。图中直线是包含无风险资产时投资者新的投资边界，称之为资本配置线，每一点代表着一组风险资产和无风险资产的投资权重。P点以下表明市场上不允许无风险资产借入的投资组合，此时，风险资产的投资权重xp<1；P点以上表明市场允许无风险资产借入的投资组合，此时xp>1。由此可知，市场的限制越少，投资者的交易范围越大，市场的活跃程度也会加大，但同时投资的风险也就越大。每一个风险资产组合的有效边界都能构建出一条资本配置线，但对于投资者来说，最优的选择是与有效边界相切的那条资本配置线上的资产配置。市场上的风险资产组合不计其数，其边界在市场组合，即图中的M点，Rf与之相连接形成的直线是斜率最大的资本配置线，称之为资本市场线。根据Markowitz理论以及之后发展起来的资本资产定价模型（CAPM）理论，这是投资者的最佳选择边界。本文对此不再深入讨论。

（2）模型求解

求解该模型仍然采用Laganerge乘子法，通过对构建的Laganerge函数进行一阶求导，则完全资产组合中风险资产和无风险资产的资产权重xp和xf与两个Laganerge乘子λ、μ满足方程组Ⅱ

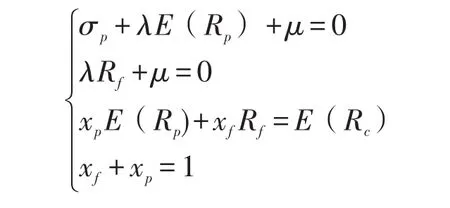
从而可得到xp和xf的值，最终构造出一个有效投资组合。

二、投资者风险控制策略

（一）投资选择

面对Markowitz均值-方差模型下构建出的有效投资组合，投资者作何选择，这与投资者对风险的主观态度——风险厌恶程度有关。有些投资者风险厌恶程度较低，会选择那些能给其带来高收益，但同时也需要承担高风险的资产组合；而有些投资者风险厌恶程度较高，会选择那些需要承担低风险，但同时只能带来低收益的资产组合。比如市场上可供选择的证券投资基金，其实质就是为不同类型投资者构建的一个在有效边界上的投资组合，风险厌恶程度高的投资者可能会选择债券型基金；风险厌恶程度低的投资者可能会选择股票型基金；而有较高风险偏好的投资者可能会选择直接投资股票。

（二）投资组合的动态调整

证券市场瞬息万变，资产的风险、收益回报特征、资产间的关联度也不是一成不变的。有些证券在某一段时间可能收益较低、风险较高，可在另一段时间收益较高、风险却有所降低，而证券间的关联度也因此会发生变化。所以，市场的变化使得构建的有效组合不再有效。对此，投资者要根据市场的变化以及对未来趋势的判断，对投资组合做出动态调整。改变组合中资产的投资比例，甚至是更换所持有证券的种类。

（三）VaR约束

证券投资过程中，风险与收益如影相随，当市场允许融资融券，投资者在追求更高收益的同时，面临的风险也无限扩大。在这样的市场中进行投资，投资者首先应该设定一个能够承担的最高风险水平，在此风险水平的约束下，寻找最佳投资组合是不错的选择。国内学者黄继平等人（2004），构建了VaR约束下的Markowitz均值-方差模型，讨论中国证券市场上基于VaR约束的证券投资决策问题，这对投资实践具有重要的指导意义。［1］

三、Markowitz均值-模型在我国证券市场上应用的实例分析

中国证券市场于2010年开展了融资融券业务，故Markowitz均值-方差模型可以直接使用，不必再做出权重大于零的约束条件。由于不包含无风险资产的Markowitz均值-方差模型和包含无风险资产的Markowitz均值-方差模型在应用中原理相同，只是组合收益的公式不同，所以本文仅使用不包含无风险资产的Markowitz均值-方差模型对我国证券市场上的应用进行实例分析。

应用实例：假定在资产选择原则的指导下，投资经理筛选出以下4只股票：中国联通、浦发银行、万科A、工商银行。所选用数据来源于锐思数据库［2］，时间是2011年1月4日～2015年1月3日，共791个交易日。基础数据计算的结果或设定如下：

（一）个股的收益回报特征

1.个股日收益的期望值、方差计算结果如下（见表1、表2、表3）：

表1 个股日收益的期望值、方差

2.股票间关联度的计算结果如下：

表2 股票间日收益率的方差-协方差矩阵

表3 股票间日收益率的相关系数矩阵

（二）投资组合的构建

根据个股的收益风险回报特征，我们构建以下三个投资组合方案（见表4）。

表4 可供选择的资产组合方案

则有：

1.组合个股日收益率的期望值矩阵Rn的结果如下：

2.组合个股日收益率的方差-协方差矩阵∑的结果如下：

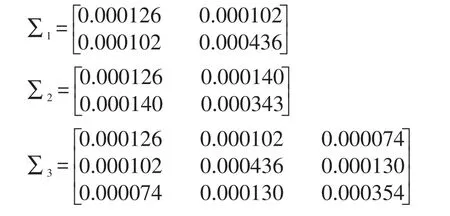
（二）不包含无风险资产的Markowitz均值-方差模型的应用实例分析

通过构建Laganerge函数，解方程组，计算结果如下：

1.组合一的权重集

2.组合二的权重集

3.组合三的权重集

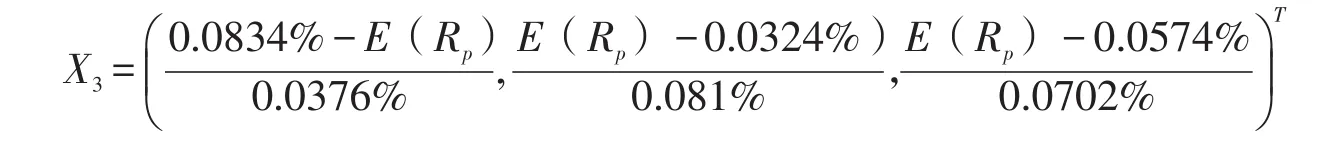
给定投资者追求的有效组合边界范围的一个期望收益率E（Rp）的值，则可以得到组合的最优投资权重向量。例如E（Rp）=0.06%，则有：

组合一的最优投资权重向量为：

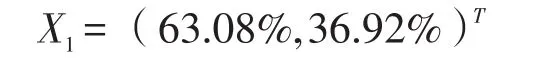
组合二的最优投资权重向量为：

组合三的最优投资权重向量为：

将权重向量代入公式（1）中，则可以计算出追求0.23%收益水平，三种投资组合面临的风险

（三）包含无风险资产的Markowitz均值-方差模型的应用实例分析

假定投资者选择组合三作为风险资产的投资，市场上的无风险资产的回报率为0.01%，解方程组Ⅱ，得到权重集

假定投资者追求0.08%的收益水平，则有xp=140%，xf=-40%，此时投资风险σc=0.021。

四、研究结论

结论一：比较组合一和组合二，构成组合的资产收益和风险水平相当，组合一中工商银行与万科A的相关系数为0.4382，组合二中工商银行与浦发银行的相关系数为0.6733。当两个组合获得相同的收益水平0.06%，所面临的风险却不同，=0.000157<=0.000163。此结果证明了Markowitz理论中相关系数对资产组合风险的影响关系，即相关系数越小，则资产组合风险就越小。投资实践中，投资者不可能一一计算资产间的相关系数，但区域间、行业间的资产相关系数通常情况下会小于区域或行业内部的相关系数。所以，投资者要跨区域、跨行业进行多元化投资，以分散风险。

结论二：比较组合一和组合三，组合一有两种资产构成，组合三有三种资产构成。两个组合同样是收益水平相同，但风险不同=0.000150<=0.000157。此结果证明了Markowitz理论中资产数目对组合资产风险的影响关系，即资产数目越大，则组合资产风险就越小。在中国市场的投资实践中，投资者可以利用此关系构建组合。

结论三：假定有一个投资者利用Markowitz资产选择原则，选择组合三中的三种资产进行投资，但没有使用Markowitz均值-方差模型确定投资权重，随意地将投资权重确定为（70.0%，60.93%，-30.93%）T。将其代入组合收益公式E（Rp）=x1R1+x2R2+…xn Rn以及公式（1）中，可以计算出：组合的收益仍保持在0.06%的水平，但风险却高达0.000263。该组合与组合三包含同样的资产，组合的收益水平相同，但却因为权重的不同，分散风险的效果降低了。这就是组合理论中所说的无效组合。运用Markowitz均值-方差模型，可以帮助投资者找到有效组合，即收益水平相同、风险最小或风险水平相同、收益最大的组合。

通过以上的实例分析及结论阐述可知，在中国投资市场上，Markowitz理论是适用的。本文的研究分析对我国的投资者，特别是投资机构、证券投资基金具有理论指导意义和现实应用价值。

［1］黄继平等.基于风险控制的证券投资决策［J］.统计研究，2004.

［2］http://www3.resset.cn:8080/product/common/main.jsp,股票综合数据.