Holder不等式再推广的几种形式

孙凤庆

山东德州职业技术学院计算机系

Holder不等式再推广的几种形式

孙凤庆

山东德州职业技术学院计算机系

本文主要对原Holder不等式进行了进一步的推广，将原Holder不等式由2个实数列推广到m(m＞=2)个实数列，同时给出推广后的Holder不等式的几种不同形式并对其加以数学证明.

Holder不等式；推广的Holder不等式；引理(Young不等式的推广)；琴生不等式；级数；Riemann积分

1.Holder不等式

设a=(a1,a2,........,an)与b=(b1,b2,..........,bn)是两个非负实数列；∂与β为两个正数,且∂+β=1

且只有当ai=0或bi=0或者存在正数k使得ai=kbi时（i=1,2,......n）等号才成立．

2.推广的Holder不等式

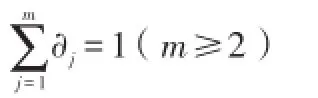
且只有当a1i=0或a2i=0……或ami=0或者存在m个正数k1,k2,......km使得k1a1i=k2a2i=......=kmami时（i=1,2,......n）等号才成立．

证明：

1）引理(Young不等式的推广)：设aj≥0(j=1,2,......m)；∂1,∂2,......∂m为m个正数，

且只有当a1=a2=......=am时，等号才成立．

证明：

①当a1,a2......am中有一个为0时，不等式显然成立

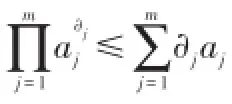
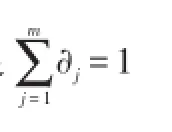
因此由琴生不等式可得：

且只有当a1=a2=......=am时，等号才成立

2）再证明推广的Holder不等式(即（1）式)

①当a1i=0或a2i=0......或ami=0时（i=1,2,......n），（1）式显然成立，且等号成立

则（1）式变为：

只需证明此不等式即可。

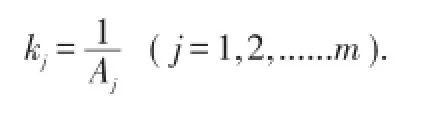
3.推广的Holder不等式的级数形式

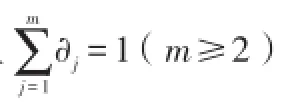
4.推广的Holder不等式的Riemann积分形式

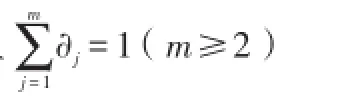
由（1）式可得:

再由极限保号性质可得（3）式成立.

注：对x∈[a,b]，只有当f1(x)≡0或f2(x)≡0...........或fm(x)≡0或者存在m个常数k1,k2,......km使得k1f1(x)≡k2f2(x)≡............≡kmfm(x)时，（3）式中等号才成立．

[1]李心灿的《Holder不等式的一种推广》一书，北京航空学院出版/1957

[2]历倩的Holder不等式的再推广及应用，《数学通迅》，2006—05

[3]熊斌的Schur不等式和Holder不等式及其应用，《数学通讯》，2005—15

[4]陶双平马国顺的一个广义Holder不等式，《安康师专学报》，1992—02

[5]胡克的论Holder不等式，《江西师范大学学报.自然科学版》，1994—03

[6]文开庭的Holder不等式的新推广，《毕节师范高等专科学校学报》，2002—01

[7]张天德韩振来的数学分析同步辅导及习题精解，天津科学技术出版社，2009，7

孙凤庆（1963-），男，副教授，大学本科（工学学士）