h-差分意义下Hölder不等式的证明及应用
肖志勇,任晓娜
1陇东学院数学与统计学院;2古战九年制学校
h-差分意义下Hölder不等式的证明及应用
肖志勇1,任晓娜2
1陇东学院数学与统计学院;2古战九年制学校
借助于普通意义下Hölder不等式的证明技巧,本文建立了h-差分意义下Hölder不等式.其次利用所建立Hölder不等式得到h-差分意义下的Cauchy-Schwarz不等式和Minkowski不等式.
h-差分分析;Hölder不等式;Cauchy-Schwarz不等式;Minkowski不等式
一、引言
差分方程理论是现在数学研究的一个重要分支,随着差分方程在数学、工程及其他领域的广泛应用[1-4],h-差分方程理论在近几年得到广泛关注[5],但是它的理论研究还很不成熟,有待于进一步探究.众所周知,Hölder不等式在泛函分析及偏微分方程等学科中发挥着重要作用,尽管连续情形下Hölder不等式的理论研究已取得丰富成果[6-8],但对离散h-差分意义下Hölder不等式研究结论仍十分罕见.基于此本文将对离散h-差分意义下的Hölder不等式进行研究.
二、基础知识及引理
以下给出h-差分基础知识,见文献[5]
对于给定实数h>0.记:
对任意a,b∈Τ,a<b,记离散区间:
对于定义在[a,b]Τ上的实函数f(t),定义其向前h-差分为
为了在下一部分证明离散h-差分Hölder不等式,我们先给出如下引理
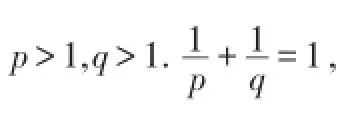
三、主要结果
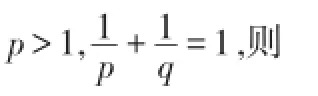
证明若f(t)≡0或g(t)≡0,t∈[a,b]Τ,则(3.1)式显然成立.所以不妨设f,g在区间[a,b]Τ上不恒为0,则
定义非负函数
由引理2.1有
即有
在(3.2)式两端同乘以
可得
证毕。
特别地,当定理3.1中p=q=2时,便可得如下h-差分Cauchy-Schwarz不等式.
定理3.2(h-差分Cauchy-Schwarz不等式)设f,g是定义在离散区间[a,b]Τ上的实函数,则
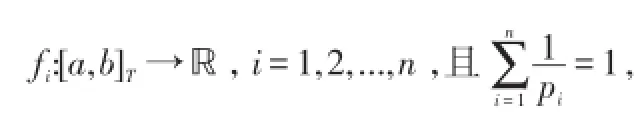
证明利用数学归纳法来证明(3.4)式.
(1)当n=2时,显然成立(即为Hölder不等式);
(2)假设当n=m时成立,即

成立.
由Hölder不等式有
由假设可知
将上式代入(3.6)式即得(3.5)式,结论得证。
接下来,我们利用Hölder不等式来推导h-差分意义下的Minkowski不等式
定理3.4(h-差分Minkowski不等式)设f,g为定义在离散区间[a,b]Τ上的实函数,则
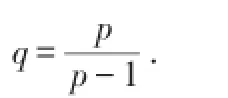
即:
便得
即(3.7)式成立. 证毕。
两边同除以
[1]阮炯.差分方程和常微分方程[M].上海:复旦大学出版社, 2002.
[2]杨清霞.浅谈差分方程的应用[J].中央民族大学学报,2006,15(3):282-285.
[3]孙清华.差分方程的应用初探[J].武汉纺织工学院学报,1999,12(3):29-32.
[4]陈泰伦,蔺小林.差分方程的理论研究与应用[J].西北轻工业学院学报,1996,14(3):128-133.
[5]Martin Bohner,Allan Peterson.Advances in Dynamic Equa⁃tions on Time Scales[M].Birkhauser,2002.
[6]孙秀华,贾洪波.Hölder不等式的推广[J].河南教育学院学报,2010,19(1):15-16.
[7]徐罕.Hölder不等式的一个应用[J].纺织高校基础科学学报,1998,11(2):177-179.
[8]兰春霞.关于Hölder不等式应用的初探[J].成都教育学院学报,2002,16(9):68-70.
[9]程其襄,张奠宙,魏国强等.实变函数与泛函分析基础[M].北京:高等教育出版社,2010.
[10]夏道行,严绍宗.实变函数与应用泛函分析基础[M].上海:上海科学技术出版社,1887.

