正十七边形尺规作图证明复数解法

李孝民

（成都七中，四川成都 610000）

正十七边形尺规作图证明复数解法

李孝民

（成都七中，四川成都 610000）

本论文对十八世纪末德国数学家约翰·卡尔·弗里德里希·高斯(Johann Carl Friedrich Gauss)所解决的正十七边形尺规作图问题再次进行了讨论。当年高斯运用了三角函数的知识求出了cos的表达式,它是数的加减乘除平方根的组合,故正17边形可用尺规作出。而本论文主要运用了复数的知识，加以结合旋转对称的思想，通过另一种途径得出了cos的表达式，与高斯用三角函数方法所得结果具有等价性。然而在借助计算机帮助的过程中，发现了所得结果与原结果的差异性并且进行了大胆尝试与复杂的运算，将所得多重根式倒推，还发现了一些多元高次方程组与一元高次方程的联系。

尺规作图 尺规作图 复数

引言

尺规作图，是从古希腊时期的几何学家们开始就一直在探讨的问题，作图所用的直尺，是没有刻度的，尺规作图最简单的应用就是平分角。古希腊数学家欧几里得已经指出，正三边形、正四边形、正五边形、正十五边形和边数是上述边数两倍的正多边形的几何作图是能够用圆规和直尺实现的，在那之后关于这个问题的研究没有多大进展。而德国数学家卡尔·弗里德里希·高斯在19岁时因为偶然的机会解决了困扰了数学家两千年之久的正十七边形尺规作图问题。继而在数论的基础上提出了可用尺规作图的正奇数边多边形的条件：尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积，解决了两千年来悬而未决的难题。

在之后的两百多年中也有很多的学者对此著名历史问题进行了研究，其中就包括R.C.Archibald，W.Bishop，P.Vélez和O.Luis等人。他们中的很多对这个历史事件重新进行了论述并且从不同角度重新看待该历史问题，然而本文即是从复数与方程组的角度重新对此问题进行了研究。

一、本文所论述的研究过程

由于受到正十七边形尺规作图过程的启发，该过程便是通过复杂的尺规作图过程将一个圆平均分成17份，然后将17个点作为正十七边形的顶点再相连，便得到所求作图形，然而因为想到这是在一个单位圆中作图，圆心指向17个顶点便可以得到17个依次夹角都为的单位向量。并且高斯用三角函数证明的过程中，便是建立了一个平面直角坐标系。由此联想到，可以建立一个复平面，其中每一个之前的向量都使之对应一个复数，因为这些向量之间都可以通过互相旋转所得，相邻两向量之间夹角又相同，于是所对应的复数之间也必然存在着很多的关系，除此之外，因为旋转，我们还可以将这17个向量所组成的集合扩展开来，得到无数的向量，不过其余的向量都与之前的这17个重合，于是可以避免很多证明过程中的限制。此外，论证到最后的时候，对四元四次方程与一元十六次方程的关系，以及用多重根式形式的解倒推其所对应的一元高次方程也进行了粗浅的讨论，绝不仅局限于对正十七边形尺规作图证明的讨论。

二、探究与证明过程

1.首先，作一个复平面（如右图），以x轴作为实轴，y轴作为虚轴，O为原点，再以O点为圆心作一个单位圆，圆上分别取，Z0， Z1，Z2......使得单位向量依次相邻两向量之间夹角都为

2.设复数Z0对应向量对应向量对应向量设，将复数用三角形式表示如下：

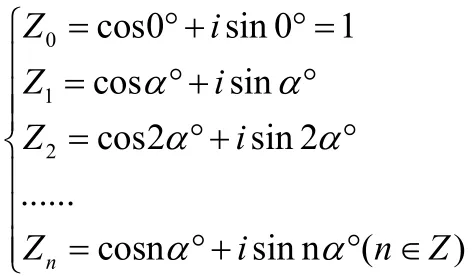
3.再由De Moive定理可得：

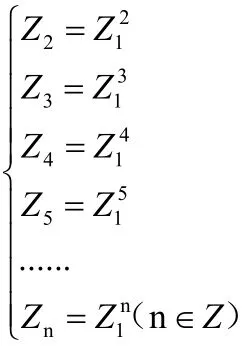
同理可得：

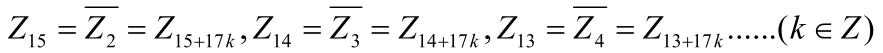
此处提供两种求法：

解法（1）利用第2、3步的结论以及平方差公式：

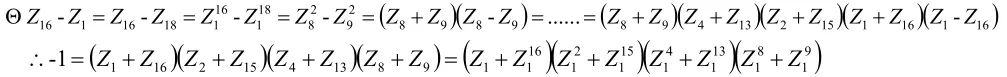
解法（2）利用第3步构造等比数列:

由于

则构成了一个首项为1，公比为Z1的等比数列。

由等比数列求和公式可得：

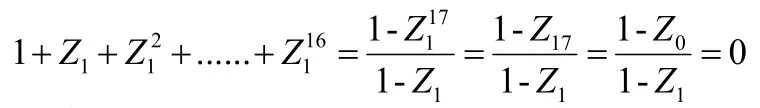
则可得同样的结果：

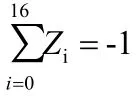
将a,b,c,d代换成复数和，再乘开可得：

7.此时可发现很多内在联系：

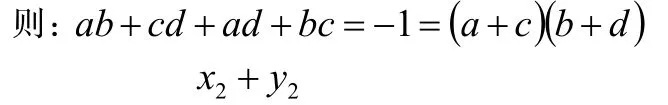
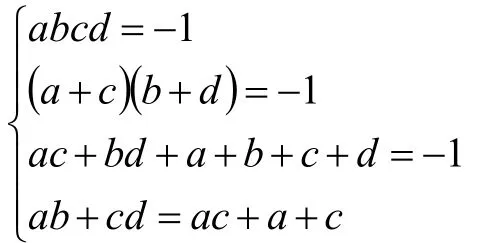
8.运用数学软件Wolfram Mathematica9.0解此方程组，所得实数解有8组。

由图象可得a,b,c,d大概范围：

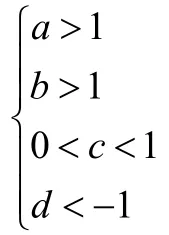
由于根式形式过于复杂，我们在实数解组中排出多余组解的步骤中暂时选取小数，并且保留六位有效数字：

Wolfram Mathematica9.0所得小数结果如下图：

显然①～④组和⑤～⑧分别都是循环的，一共相当于是八组包括循环对称的实数解。

根据a,b,c,d大概范围，可以排除其余七组，最后只剩下：

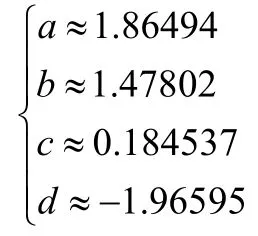
9.实际上Wolfram Mathematica9.0得到根式结果的过程如下图：

第一步：

第二步：

第三步：

第四步：

第五步：

第六步：

第七步：

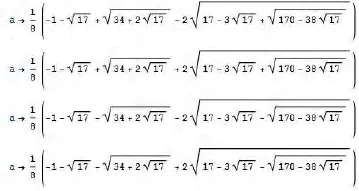
这样，我们就得到了根式形式的所有实数解。

再结合之前的小数，将其与根式形式对应：

11.高斯用三角函数法所求：

所以用本文复数方法所得结果与高斯方法所得结果具有等价性。

13.四元四次方程组与一元十六次方程

以上关于正十七边形尺规作图证明的过程已经完成，下面我们由方程组所得三重根式解引发的思考进行简单粗略的讨论：

（1）借助Wolfram Mathematica9.0的帮助，我们可以知道

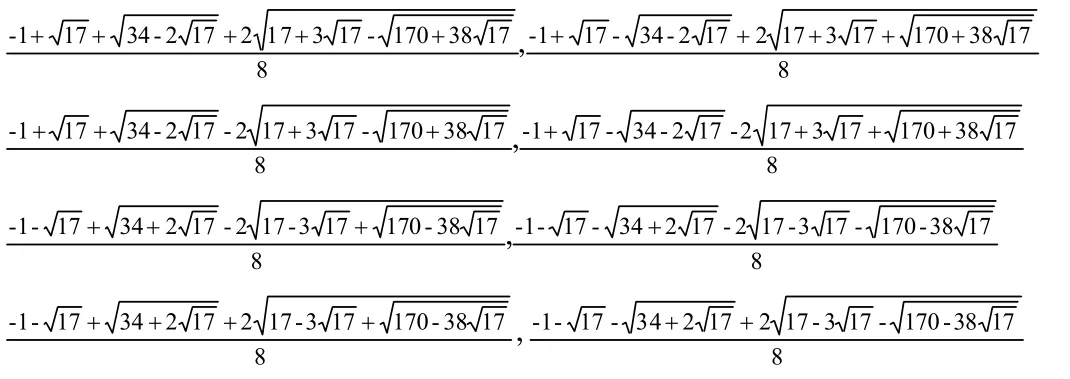
八个实数解实际上是一元八次方程x8+x7-7x6-6x5+15x4+10x3-10x2-4x+1=0的八个解，而其余八个虚数

八个虚数解实际上是一元八次方程x8+2x7+3x6+2x5+3x4+6x3+7x2+4x+1=0的八个解。

将两个一元八次方程相乘，我们便可以得到，原四元四次方程组的四个实数解和四个虚数解就是下面一元十六次方程的解：

所以说该四元四次方程组与这个一元十六次方程是对应的（即使方程组的解为循环对称的）。

（2）观察解的形式，可以发现最多即是三重根式，而且不论是实数解还是虚数解都是两两共轭的。现在我们将要尝试通过解来倒推出一元十六次方程。首先我们举一个例子来分析：

这样子我们就通过一个根式解逆向推导出了含有这个解得一元二次方程。由这个例子我们可以得到启发：我们可以先把三重根式移到方程一边，然后再两边平方，接下来是二重，一重，直到整个方程不再含有根式，我们便得到了一个含有该解的整系数方程。根据代数数的定义描述：代数数指任何整系数多项式的复根，即若x是一个代数数，那么必然存在整数使得x是以下方程:由于“任何可以从整数或有理数通过有限次四则运算和正整数次开方运算得到的数都是代数数”，而此时四元四次方程组的根即为代数数，我们便可以尝试将其作为一个整系数方程的根。

（3）然而经过了十分复杂的运算，最终得到的是这样一个一元十六次方程：

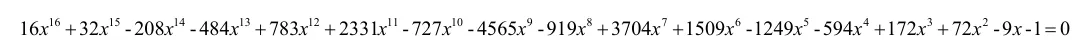
这个结果不免令人疑惑，然而我们再次借助数学软件Wolfram Mathematica9.0的帮助，将方程左边分解因式，分解到最简时即得到两个八次式的乘积，两个式子分别是和于是我们便可以发现：即是之前八个实数解对应的一元八次方程的左边部分。所以我们通过选取形式相似且两两共轭的八个实数解中的一个来推导，的确推导出了一个含有该八个解对应的八次式作为其中一个因式的一元十六次方程。

（4）由于八个实数解结构形式相似，八个虚数解结构形式也相似，但是实数解和虚数解之间就是千差万别，经过以上推导得到的结果，我们可以猜想：选取一个复数解进行推导时也是得出类似的结果。但是如果我们同时选取了实数和复数或许会得到不同结果。此处有两种尝试：

尝试1：选取一个实数解（设为x1）和一个虚数解（设为x2），那么我们可以尝试用(x-x1)(x-x2)=0这样的方法来尝试推导一个既含有实数解对应八次式又含有虚数解对应八次式的一元高次方程。

尝试2：选取两个共轭的实数解（设为x1和x2）和两个共轭的虚数解（设为x3和x4），那么我们可以尝试用(x-x1)(x-x2)(x-x3)(x-x4) =0的方法推导，或许可以简便我们的运算，因为共轭我们便可以使用平方差公式。这样可以尽量减少平方次数，从而尽量减少方程次数。

（5）然而经过实践，由于还含有虚数单位i需要化去等原因，很遗憾两种尝试的结果都是高于16次的方程。但是我们仍然可以确定的是这个四元四次方程组对应着一个一元十六次方程。

14.我们下面尝试这种方法能否推广：

凭借高斯得出的正多边形尺规作图条件，17以后的费马质数是257，由于数值太大所以我们仅讨论17之前的费马质数，即3和5。

我们首先进行边形（即正三边形）的试验：

可见此方法同样适用于正三边形。

接下来进行边形（即正五边形）的试验：

同样地，

将a,b作为方程x2+x-1=0，解此方程再结合可得

可见此方法同样适用于正五边形。

结论

德国数学家卡尔·弗里德里希·高斯大学二年级时得出正十七边形的尺规作图法，并给出了可用尺规作图的正多边形的条件。解决了两千年来悬而未决的难题，1799年以代数基本定理的四个漂亮证明获博士学位。而当年的他是运用了三角函数的知识求出了的表达式。考虑到三角函数和复数之间有千丝万缕的联系，论文就主要尝试了运用复数的知识，结合复平面中各向量旋转对称的关系，还借助了计算机的帮助，从一开始的图形与复数运算的问题最终转化到了高次方程组的问题，得出一个四元四次方程组，并利用数学建模软件Mathematica得出该方程组的所有复数解。根据未知数的范围排除其余各组解以后，最终将符合的一组解带入，得出的结果与高斯用三角函数方法所得结果相比较发现两个结果相等。然而本文不仅仅局限于对该历史问题提出另一种解决方法，更针对于在证明过程中的一些发现提出了新的猜想并进行了大尝试和研究。首先是针对证明最后的四元四次方程组的根式形式解讨论了所对应的一元十六次方程并且发现了其与方程组的对应关系。之后又进行了本文所论述方法的推广，根据高斯得到的判断正多边形能够尺规作图的条件讨论了当边数等于另外两个费马质数3和5的情况，发现同样适用，所以此方法具有一定的推广性，但对于数值稍大的费马素数找到方程组则有一定困难。此外本文论证过程还有其他缺点，比如简洁性不够，相对于高斯的三角函数的方法，本文的论证方法则十分复杂。并且在将图形的问题转化为方程的过程中则丧失了原有的对称美以及寻找内在联系时找到了四个方程，但内在联系很多，或许能够找到更多的方程。

[1]Gauss,C.F.§365 and 366 in“Disquisitiones Arithmeticae”. Leipzig,Germany:Fleischer,1801.Reprinted in New Haven,CT: Yale University Press,1965.

[2]Archibald,R.C."The History of the Construction of the RegularPolygon ofSeventeen Sides." Bull.Amer.Math.Soc.22, 239-246,1916.

[3]Archibald,R.C."Gauss and the Regular Polygon of Seventeen Sides."Amer.Math.Monthly 27,323-326,1920.

[4]Bishop,W."How to Construct a Regular Polygon."Amer. Math.Monthly 85,186-188,1978.

[5]Dickson,L.E."Construction of the Regular Polygon of 17 Sides."§8.20 in Monographs on Topics of Modern Mathematics Relevant to the Elementary Field(Ed.J.W.A.Young).New York: Dover,pp.372-373,1955.

[6]Hardy,G.H.and Wright,E.M."Construction of the Regular Polygon of 17 Sides."§5.8 in An Introduction to the Theory of Numbers,5th ed.Oxford,England:Clarendon Press,pp.57-62,1979.

[7]Richmond,H.W."A Construction for a Regular Polygon of Seventeen Sides."Quart.J.Pure Appl.Math.26,206-207,1893.

[8]Smith,L.L."A Construction of the Regular Polygon of Seventeen Sides."Amer.Math.Monthly 27,322-323,1920.

[9]Vélez,P.and Luis,O."A Chord Approach for an Alternative Ruler and Compasses Construction of the 17-Side Regular Polygon." Geom.Dedicata 52,209-213,1994.

致谢：特别感谢指导老师祁祖海在整个过程中耐心的指导，包括遇到各种问题都帮助提出策略进行尝试，以及对整篇文章的思路进行了正确引导。其次还要感谢百度贴吧好友 qsd573在利用数学软件Wolfram Mathematica9.0过程中的帮助。

This article focuses on the problem of the construction of a regular heptadecagon by ruler and compass which had been solved by the German mathematician Johann Carl Friedrich Gauss in the end of the eighteenth century.In 1798,Gauss used the method of trig function and got the expression of cos,which is the combination of the addition,subtraction,multiplication,division and square root of numbers,demonstrating that a regular heptadecagon can be constructed by ruler and compass.This article mainly applies the complex number as the tool,combining with the thought of rotation and reflection,and gained the expression of cosin another way.There is a obvious equivalence between the result using this method and the result of Gauss using the trig function as the tool.However,with the help of the computer,I found the differences between these two results and did some daring tries and complex operations.By reversely deducing the equation using the complex quadratic radical as the solution of it,I also discovered some relations between univariate equation of higher degree and multivariate equation set of higher degree.

construction with ruler and compass,regular heptadecagon,complex number