中考数学阅读题的破解方法

田义银

（重庆市开县西街中学）

中考数学阅读题的破解方法

田义银

（重庆市开县西街中学）

读懂数学新定义，联系新旧知，类比寻办法；抓数学题目中关键词的阅读与分析，迅速理解题目数量之间的内在关系，理顺变量关系，确定解题思路。重视最基本的策略——综合与分析，挖掘、整理数学信息之间的内在关系，理解理解数学问题，分析数量关系、寻找解题窍门，建立数学模型，实现由已知到未知的推导。

数学阅读 类比解决 数学信息 理顺变量关系 综合与分析

一、读懂新定义，联系新旧知，类比寻方法。

不少数学中考阅读理解题，要求学生读懂新定义，需运用所学新旧知识类比解决解决数学实际问题。

例如：甘肃兰州数学中考第26题。通过学习三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.类似的，可以在等腰三角形中建立边角之间的联系.我们定义：等腰三角形中底边与腰的比叫做顶角正对（sad），如图①，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sadA=底边/腰容易知道一个角的大小与这个角的正对值也是相互唯一确定的。根据上述角的正对定义，解下列问题：（1）sad60°=_____。（2）对于0°＜A＜180°，∠A的正对值sadA的取值范围是______。（3）如图②，已知其中∠A为锐角，试求sadA的值。

分析：（1）根据等腰三角形的性质，求出底角的度数，判断出三角形为等边三角形，再根据正对的定义解答当∠A接近0°时，sadα接近0，当∠A接近180°时，等腰三角形的底接近于腰的二倍，故sadα接近2. 于是sadA的取值范围是0＜sadA＜2；（3）作直角△ABC，在AB上取点D，使AD=AC，构造等腰三角形ACD，作DH⊥AC，H为垂足，令BC=3k，AB=5k，求出AD=AC=4k，在△CDH中，计算CD的值，由正对的定义可得

二、抓关键，理顺变量关系，确定解题思路

例如：重庆数学中考第25题。企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行。1至6月，该企业向污水厂输送的污水量y1（吨）与月份x（1≤x≤6，且x取整数）之间满足的函数关系如下表：

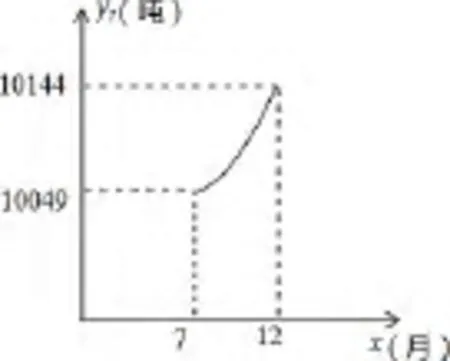
7至12月，该企业自身处理的污水量y2（吨）与月份x（7≤x≤12，且x取整数）之间满足二次函数关系式为其图象如图所示。1至6月，污水厂处理每吨污水的费用：z1（元）与月份x之间满足函数关系式该企业自身处理每吨污水的费用：z2（元）与月份x之间满足函数关系式7至12月，污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元.

（1）观察题中的表格和图象，用所学过的一次函数、反比例函数或二次函数的有关知识，分别直接写出y1'y2与x之间的函数关系式；（2）请你求出该企业去年哪个月用于污水处理的费用W（元）最多，并求出这个最多费用；（3）今年以来，由于自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%，同时每吨污水处理的费用将在去年12月份的基础上增加（a-30）%，为鼓励节能降耗，减轻企业负担，财政对企业处理污水的费用进行50%的补助. 若该企业每月的污水处理费用为18000元，请计算出a的整数值

分析：这个题的考点是一次函数、反比例函数和二次函数的应用，有图表，有图像，还有大量的文字需要阅读。如何通过对关键词的阅读与分析，迅速理解本题的数量之间的内在关系，理顺变量关系，确定解题思路，是解决这类题的重要策略。

①从表格中数据看x与y1的乘积是一个定值12000，故y1与x之间的函数关系为反比例函数关系：y1=（1≤x≤6，且x取整数）。

②从图像看y2是x的二次函数，图像的两个关键点是（7，10049），（12，10144）。代入得a、c的值。

③该企业去年1至6月污水处理的费用W（元）包括污水厂处理每吨污水的费用z1（元）和该企业自身处理每吨污水的费用z2（元）两部分。W= y1+（12000-y1）1·z2

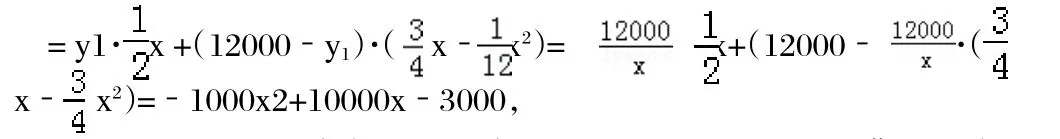
④去年7至12月该企业污水给污水厂处理每吨污水的费用均为2元，该企业自己处理每吨污水的费用均为1.5元。因此处理污水的费用

三、重视最基本的策略——综合与分析，寻找解题窍门

分析是把整体分解成若干部分，通过对每一部分的研究，实现对整体的了解。分析这种思维方法就是把所求问题作为思考切人口，推理出需要的条件。综合是把几个有关系的部分，按某种联系组织成整体。综合这种阅读方法就是从研究条件间的联系切入，逐渐向所求问题逼近。实际问题里有许多数学信息，包括已知条件、所求问题以及相互联系，共同组成可解决的问题。这里的综合阅读不只是指阅读文字，还包括图表等，他要求我们从几个方面入手。如果题目没有图表，但我们读了文字没有太多的印象，那么就应该根据题目自己画出图表，并思考：告诉我这个条件有什么用？由这个条件我们可以得到什么结论。挖掘、整理数学信息之间的内在关系，理解理解数学问题，分析数量关系、寻找解题窍门，建立数学模型，实现由已知到未知的推导。

学生阅读数学信息解决问题的经验，如策略、方法、书写、检验等，势必促进学生阅读数学题目思维的深刻性、批判性、抽象性、灵活性、条理性和独创性等品质的提升。