属性层级模型的改良及诊断性能研究*

韩裕娜，张敏强，方 杰

(1.华南师范大学心理应用研究中心，广州510631;2.华南师范大学基础教育培训与研究院，广州510631;3.广东财经大学人文与传播学院，广州510320)

1 引言

《国家中长期教育改革和发展规划纲要(2010-2020 年)》提出，在党和国家工作全局中，必须始终坚持把教育摆在优先发展的位置，坚持育人为本，以改革创新为动力，以促进公平为重点，以提高质量为核心，全面实施素质教育，推动教育事业在新的历史起点上科学发展。测量理论和技术为教育改革提供了支持，只有通过科学的测量才能准确地知道学生的真实情况，才能因材施教，培养出高素质人才，促进教育事业科学发展。

然而基于经典测验理论、概化理论和项目反应理论的传统测验最终只能给出一个分数或等级。但是有的考生分数或等级虽然相同，所掌握的知识却不同。为了从考生的反应模式中获得更多考生的信息，进而因材施教，许多研究者都做了一些尝试，他们认为其中的一个出路就是“将认知与测量相结合”，并沿着不同的路线，按照不同的假设，提出了各自不同的认知诊断模型。

AHM 模型是影响较大的认知诊断模型之一。该研究将以AHM 模型为研究对象，首先简单介绍AHM 模型及其诊断步骤，分析方法A 和方法B 的计算公式，对其进行改良得到两种新分类方法——方法C 和方法D。并以模式判准率和边际判准率为评价指标，通过两个蒙特卡洛模拟实验探讨各种测验因素对A、B、C、D 四种诊断方法分类准确率的影响，为使用者(研究者)在不同测验情景下该选择哪种方法提供有益的参考。

2 AHM 模型简介

AHM 模型是由Leigton 等人(2004)对RSM 模型进行改造而产生的。使用属性层级模型进行认知诊断共 包 含 四 个 步 骤(Gierl，Leighton，＆ Hunka，2007):(1)构建和表征测验内容的属性层级模型;(2)根据层级关系模型编制测验并施测;(3)使用一种判别方法，根据被试作答情况，对被试进行诊断分类;(4)报告认知诊断分析结果。

AHM 中分类方法有两种IRT 分类法(Leigton，2004):方法A 和方法B。方法A 和方法B 都是通过分析观察反应模式同各类期望反应模式的一致程度来进行分类。

方法A 认为，当被试的观察反应模式和任何一类期望反应模式都不一样时，则计算各种期望反应模式转化为观察反应模式的概率，假设第p 种期望反应模式的转化概率最大，则将被试归为第p 类被试。转化概率的计算公式如下:

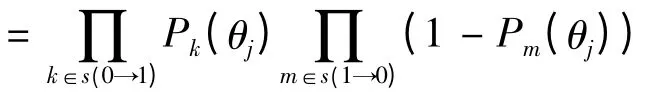
其中:

Si(0 →1)表示对于被试i 期望反应为0，但观察反应模式为1 的所有题的集合;

Si(1 →0)表示对于被试i 期望反应为1，但观察反应模式为0 的所有题的集合;

方法B 则认为，拥有某个观察反应模式的被试掌握了所有逻辑包含在其中的期望反应模式的属性组合。方法B 计算转化概率的公式如下:

3 方法A 和方法B 的改良

以往的研究(Cui，Leighton，＆ Zheng，2006)表明，方法A 和方法B 的诊断准确率均不高，说明这两种方法还有待进一步改进。仔细查看方法A 的计算公式，可以发现:方法A 在判别具有观察反应模式Si的被试是否属于第j 类被试时，计算和比较的是第j类被试出现观察反应模式Si的概率，使用到的是正确作答概率Pk(θj)和错误作答概率1 - Pk(θj)。

事实上，在对被试进行诊断时，并不知道他到底是哪一类被试，也不知道他是否真的掌握对应题目所考察的属性.因而方法A 在判别被试属于哪一类时使用上述概率并不合理，这应该是方法A 诊断准确率不高的一个原因。在判别具有观察反应模式Si的被试是否属于第j 类被试的关系时，计算和比较的应该是具有观察反应模式Si的被试是第j 类被试的概率。

因而使用到的概率应该是另2 种:

(1)当受测者答对试题q 时，受测者实际上并未掌握试题q 所考察的属性的概率P(q:1 →0)，称为猜测概率，用PG(q)表示。

(2)当受测者答错试题q 时，受测者实际上掌握了试题q 所考察的属性的概率P(q:0 →1)，称为失误概率，用PS(q)表示。

由方法A 的计算公式，以猜测概率PG(q)和失误概率PS(q)代替Pk(θj)、1 - Pm(θj)，即得到判别方法C:计算具有观察反应模式Si的被试是各类被试的概率，假设第p 类被试对应的概率最大，则将被试归为第p 类被试。

同样地，可由方法B 得到对应的D 方法，D 方法使用的公式如下:

4 模拟研究

从理论上看，方法C 和方法D 的计算方法比方法A 和方法B 更为科学，应该比方法A 和方法B 有更高的诊断性能。为了比较新旧四种方法——方法A、方法B、方法C 和方法D 的诊断性能，拟通过蒙特卡洛模拟实验，采用随机化实验，针对四种判别方法的诊断性能进行考察。

文剑兵(2003)和田伟等人(2012)的研究表明，规则空间模型的诊断性能会受到属性结构、属性个数、失误水平的影响;Cui，Leighton 和Zheng(2006)的研究也表明，属性层级模型方法A 和方法B 的诊断性能也会受到属性结构、失误水平的影响。因此，AHM 四种判别方法评价指标的高低除了跟诊断方法有关，还有可能受其他因素影响，例如:属性的结构、属性个数和失误水平等因素有关。本研究共设计了两个模拟实验来讨论不同因素对四种诊断方法的分类准确率的影响，同时比较四种诊断方法的诊断性能。比较诊断性能时采取两种评价指标——模式判准率和边际判准率，评价指标越高，说明分类准确性越好。

4.1 实验一 属性的结构和个数对诊断性能的影响

4.1.1 研究设计

实验一旨在考察属性的结构和个数对诊断性能的影响。由于属性间的复杂关系可由四种基本关系组合生成，其他复杂的关系可以由这四种基本关系组合 生 成(Leighton，Gierl，＆ Hunka，2004;Cui，Leighton，＆ Zheng，2006)。参照以往研究(文剑兵，2003;Cui，Leighton，＆ Zheng，2006;丁树良，汪文义，杨淑群，2011;田伟，辛涛，2012)，实验一将考察四种属性结构(发散型、收敛型、线型、无结构型)和四种属性个数(6、7、8、9)(图1、图2、图3、图4)对四种判别方法诊断性能的影响，实验一共有4 ×4 =16 种实验情景。

图1 六个属性的四种属性层级关系

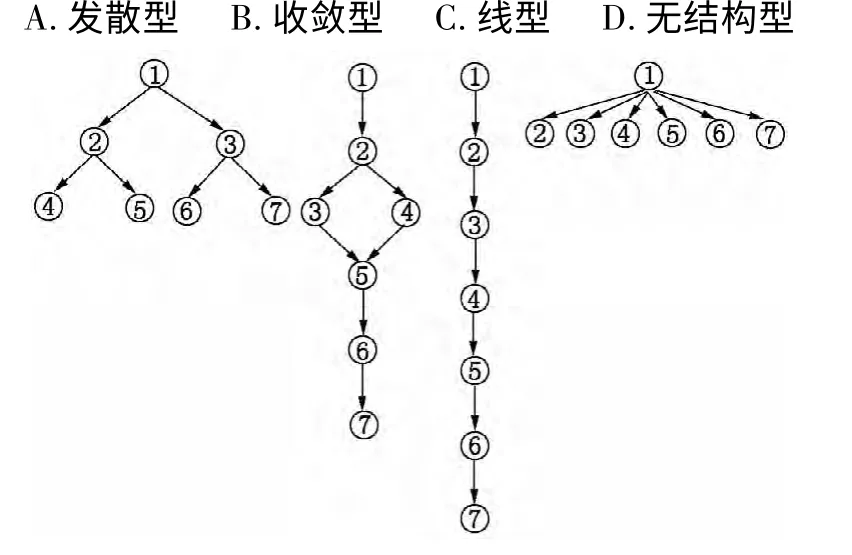
图2 七个属性的四种属性层级关系

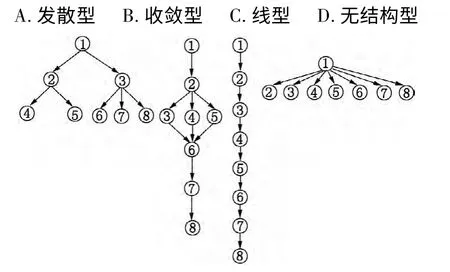
图3 八个属性的四种属性层级关系

图4 九个属性的四种属性层级关系

其他测验条件假定如下:测验项目数设置为20;被试成绩的先验分布假设为正态分布，参与诊断的被试人数为5000;IRT 模型选取二参数Logistic IRT模型;失误水平参数假定为0.1。

4.1.2 数据的产生和分析

各种实验情景下产生数据和分析数据的模拟步骤相同。在每种实验情景中，模拟步骤如下:首先依据假设的条件，模拟产生试题、得到期望反应矩阵和观察反应矩阵;接着编程估计被试能力参数及项目参数;再分别使用AHM 模型四种分类方法对观察反应模式进行诊断，计算各自的模式判准率和边际判准率;为了尽量减少无关变量的影响，每种实验情景重复模拟10 次;最后，求十次模拟各种指标的平均值，分析比较各种情境下各种方法的诊断性能指标，得到实验结果。整个数据的产生和分析过程均采用R 软件编程实现。

4.1.3 实验结果

实验一共16 种测验情景，结果如表1 所示，每一个单元格中的统计量值均是10 次模拟结果的平均，以此降低误差。

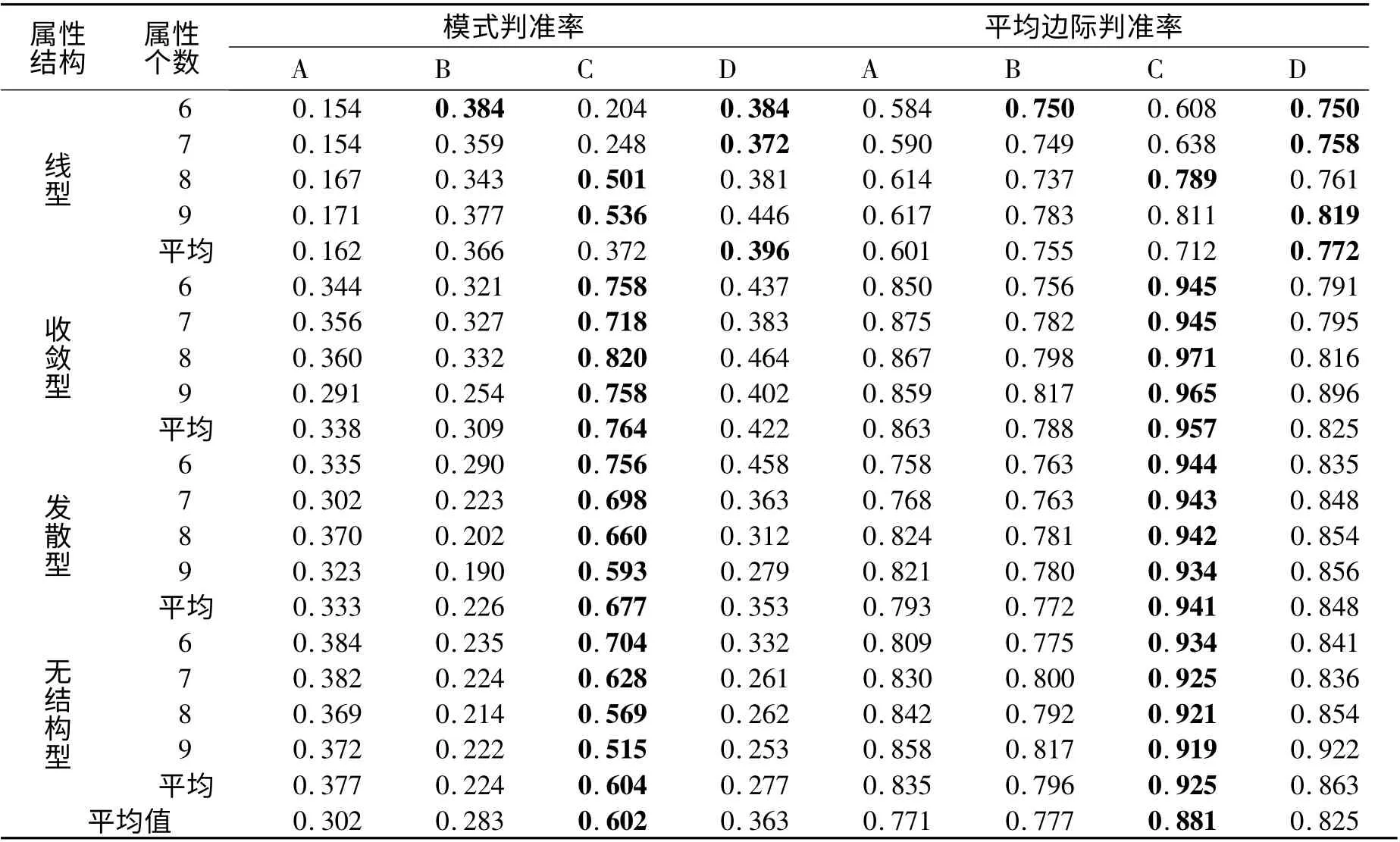
表1 实验一各种诊断方法的属性诊断准确率

4.2 实验二 失误水平参数对诊断性能的影响

4.2.1 研究设计

实验二旨在考察失误水平对各种方法诊断性能的影响。由于实验一和以往的研究(Cui，Leighton，＆ Zheng，2006)均表明，属性结构对诊断性能的影响非常明显，所以在实验二中，仍分别考察四种属性结构:发散型、收敛型、线型、无结构型。失误水平则共考察5 种情形:0.05、0.1、0.15、0.2、0.25。实验二共有4 ×5 =20 种实验情景。其他测验条件假定如下:测验项目数设置为20;属性个数为7 个;被试成绩的先验分布假设为正态分布，参与诊断的被试人数为5000;IRT 模型选取二参数Logistic IRT 模型。

4.2.2 数据的产生和分析

实验二的模拟数据产生和分析的方法步骤同实验一，数据的产生和分析也是采用R 软件编程实现。

4.2.3 实验结果

实验二共20 种测验情景，对相同的模拟数据，使用方法A、方法B、方法C、方法D 分别诊断，结果如表2 所示，每一个单元格中的统计量值均是10 次模拟结果的平均，以此降低误差。

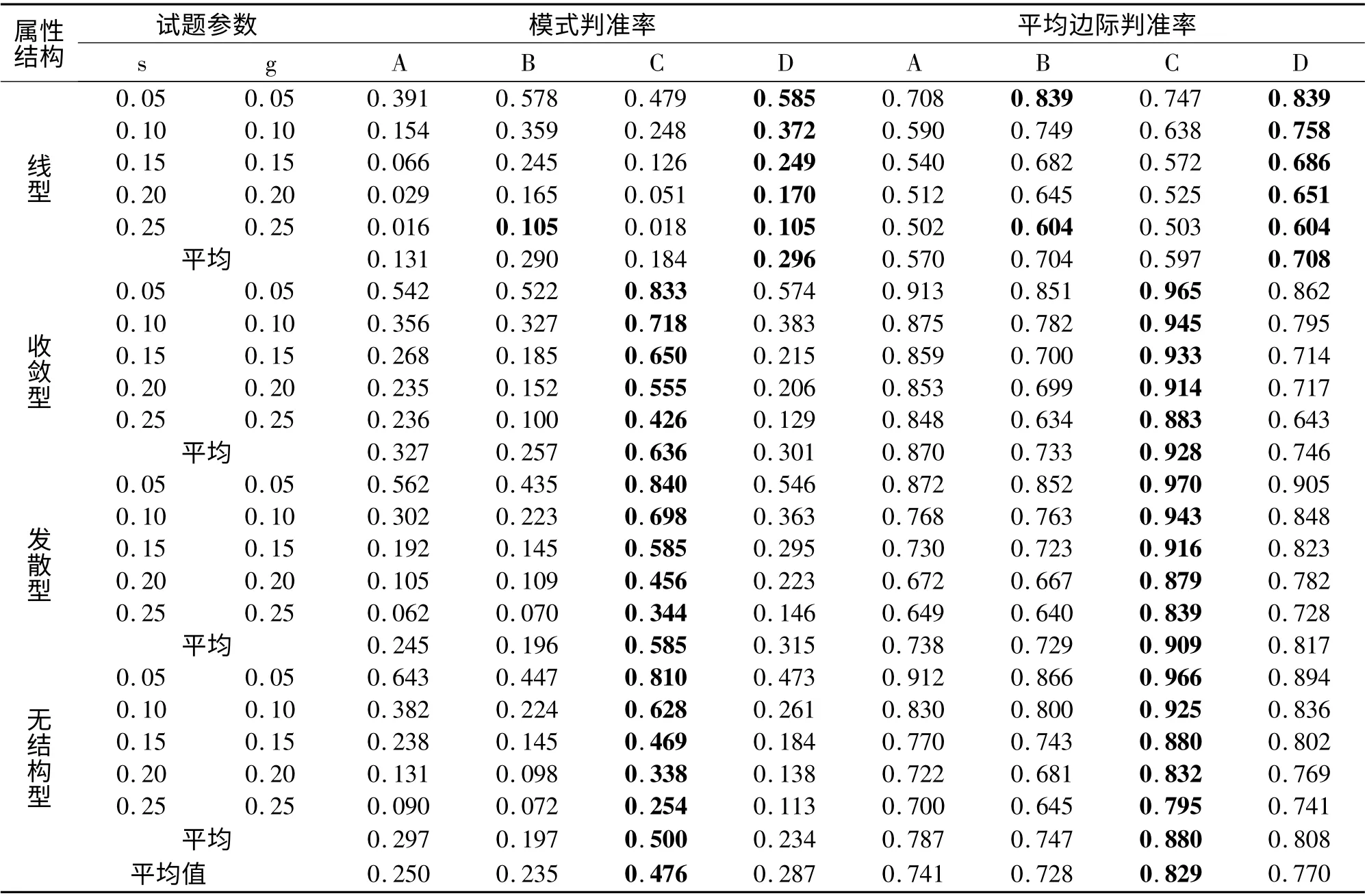
表2 实验二各种诊断方法的属性诊断准确率

5 分析与讨论

5.1 四种诊断方法诊断性能的比较

实验一和实验二的结果(表1、表2、图5、图6)表明，蒙特卡洛模拟实验的结果与理论研究结果相符，经过改良得到的方法C 和方法D 的诊断性能均优于对应的原方法。且从总体上看，新方法的评价指标比对应原方法的评价指标有较大幅度的提高。使用方法C 和方法D 更能准确地得到被试真实的知识状态和认知结构，为教学提供更为准确的诊断结果。从总体上看，四种诊断方法中C 方法最佳。

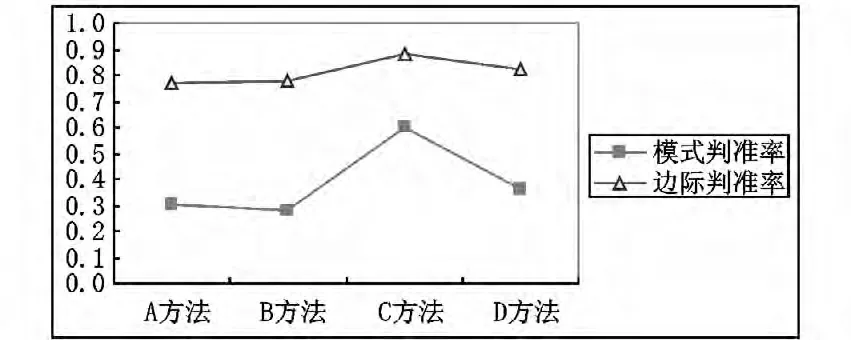
图5 实验一四种诊断方法对应的诊断指标平均数

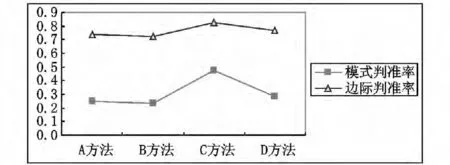
图6 实验二四种诊断方法对应的诊断指标平均数

图5 和图6 也表明，虽然实验一和实验二的实验情景不同，但是两个实验得到的结果非常一致。两个实验均表明，该研究对方法A 和方法B 的改良是成功的。

5.2 属性结构对诊断性能的影响

实验一和实验二的结果(表1、表2)表明，属性结构对诊断性能的影响非常明显。由表1 计算可得实验一16 种实验情景中，线型、收敛型、发散型、无结构型四种结构对应的诊断指标的平均数，如图7所示。由表2 计算可得实验二20 种实验情景中，线型、收敛型、发散型、无结构型四种结构对应的诊断指标的平均数，如图8 所示。由图7 和图8 可见，两个实验得到的结果非常一致，从总体上看，线型结构对应的各种诊断指标最低。而其他三种结构对应的诊断指标相差不大。四种基本结构中，收敛型结构对应的诊断指标最高。

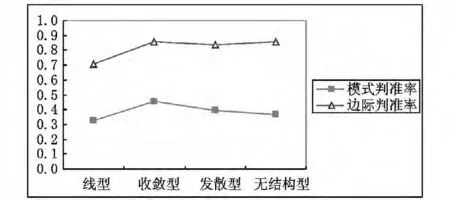
图7 实验一四种属性结构对应的诊断指标平均数

图8 实验二四种属性结构对应的诊断指标平均数

从实验一结果(表1)也可以看到，对线型结构进行诊断，最优方法是D 方法，平均边际判准率在0.7 以上。不过模式判准率还是偏低，仅有0.396。对其他结构进行诊断，最优方法是C 方法，平均边际判准率均在0.9 以上，模式判准率均在0.6 以上。由此可见，使用D 方法对线型结构进行诊断虽然最优，但是模式判准率还是偏低。相对来说，使用C方法对发散型、收敛型和无结构型三种属性结构进行诊断的各项指标则较好。使用C 方法对发散型、收敛型和无结构型进行诊断对教学有一定借鉴作用。实验二的结果和实验一一致。因而在设计测验时，不妨设法增加待测属性，使线型结构转化为发散型、收敛型或者由基本关系组合生成的复杂结构，以便提高诊断准确率。

5.3 属性个数对诊断性能的影响

表1 表明，当属性结构一样而测验属性个数不同时，诊断指标的大小会有变化，有些变化还存在一定的规律。例如，使用C 方法来诊断发散型和无结构型，各种诊断指标会随着属性个数的增多而降低。而使用方法A、C 方法来诊断线型结构，各种诊断指标会随着属性个数的增多而提高。

由表1 可以计算实验一16 种实验情景中，不同属性个数对应的诊断指标的平均数，如图9 所示。图9 表明，虽然不同属性个数对应的各种诊断指标有所差异，不过从总体上看，属性个数对诊断性能的影响不明显。

图9 实验一四种属性个数对应的诊断指标平均数

5.4 失误水平对诊断性能的影响

由表2 表明，不管对于哪种属性结构，不管使用哪种诊断方法，当失误水平参数变大时，诊断性能指标均下降。

由表2 可以计算实验二20 种实验情景中，不同失误水平对应的诊断指标的平均数，如图10 所示。图10 表明，当失误水平参数变大时，各种诊断指标均逐步下降。究其原因，失误水平参数变大说明出现猜测现象和失误现象的概率比较大，因而提高了诊断的难度，故诊断准确率有所下降，诊断性能指标逐渐变小。

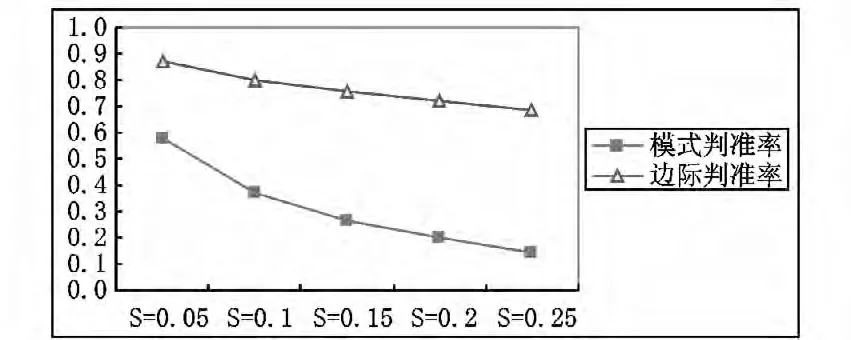
图10 实验二五种失误水平对应的诊断指标平均数

6 结论

本研究对AHM 模型两种IRT 分类方法方法A和方法B 进行改良，得到两种新方法方法C 和方法D。进而以模式判准率和边际判准率为评价指标，通过两个蒙特卡洛模拟实验来比较新旧四种方法的诊断性能，以及考察四种分类方法的诊断性能如何受到测验不同的因素的影响，为使用者(研究者)在不同测验情景下该选择哪种方法提供有益的参考。

6.1 不管是以哪种评价指标为依据，方法C 优于方法A，方法D 优于方法B，即新方法比对应的原方法有更好的诊断性能。总的来说，C 方法的诊断性能最佳。

6.2 各种方法诊断指标的高低跟属性结构有关。对线型结构进行诊断，D 方法的各种诊断指标最高;对其他三类结构进行诊断，C 方法的各种诊断指标最高。

6.3 测验属性个数对各种方法诊断性能的影响不明显。

6.4 各种方法的各种诊断性能指标随着失误水平参数提高而降低。

陈秋梅，张敏强. (2010). 认知诊断模型发展及其应用方法述评.心理科学进展，18(3)，522 -529.

丁树良，汪文义，杨淑群. (2011). 认知诊断测验蓝图的设计.心理科学，34(2)，258 -265.

丁树良，杨淑群，汪文义.(2010).可达矩阵在认知诊断测验编制中的重要作用.江西师范大学学报(自然科学版)，34(5)，490 -494.

田伟，辛涛.(2012).基于等级反应模型的规则空间方法.心理学报，44(1)，249 -262.

涂冬波，蔡艳，戴海崎，漆书青. (2008). 现代测量理论下四大认知诊断模型述评.心理学探新，28(2)，63 -67.

文剑冰.(2003).规则空间模型在诊断性计算机自适应测验中的应用.博士论文.香港中文大学.

张敏强，简小珠，陈秋梅.(2011).规则空间模型在瑞文智力测验中的认知诊断分析.心理科学，34(2)，266 -271.

祝玉芳.(2008).RSM 改进及多级评分AHM 的开发研究.硕士学位论文.南昌:江西师范大学.

Cui，Y.，Leighton，J. P.，Gierl，M. J.，＆ Hunka，S. (2006). A person-fit statistic for the attribute hierarchy method:The hierarchy consistency index. Paper Presented at the Annual Meeting of the National Council on Measurement in Education，San Francisco，CA.

Cui，Y.，Leighton，J.P.，＆ Zheng，Y.(2006).Simulation studies for evaluating the performance of the two classification methods in the AHM. Paper Presented at the Annual Meeting of the National Council on Measurement in Education，San Francisco，CA.

Gierl，M.J. (2007). Making diagnostic inferences about cognitive attributes using the rule space model and attribute hierarchy method. Journal of Educational Measurement，44，325 -340.

Gierl，M.J.，＆ Leighton，J.P.(2007).Part C:Future challenges in psychometrics:Linking cognitively-based models and psychometric methods. In C. R. Rao ＆ S. Sinharay(Eds.)，Handbook of statistics:Psychometrics(Volume 26，pp.1103 -1106).North Holland，UK:Elsevier.

Gierl，M.J.，Bisanz，J.，Bisanz，G.L.，Boughton，K.A.，＆ Khaliq，S.N. (2001).Illustrating the utility of differential bundle functioning analyses to identify and interpret group differences on achievement tests. Educational Measurement:Issues and Practices，20，26 -36.

Gierl，M.J.，Cui，Y.，＆ Zhou，J.(2009).Reliability and attribute- based scoring in cognitive diagnostic assessment. Journal of Educational Measurement，46，293 -313.

Gierl，M.J.，Leighton，J.P.，＆ Hunka，S.(2000).Exploring the logic of Tatsuoka’s rule -space model for test development and analysis. Educational Measurement:Issues and Practice，19，34 -44.

Gierl，M.J.，Leighton，J.P.，＆ Hunka，S.(2007).Using the attribute hierarchy method to make diagnostic inferences about examinees’cognitive skills. In J. P. Leighton ＆ M. J. Gierl(Eds.)，Cognitive diagnostic assessment for education:Theory and applications(pp.242 -274).Cambridge，UK:Cambridge University Press.

Gierl，M. J.，Wang，C.，＆ Zhou，J. (2008). Using the attribute hierarchy method to make diagnostic inferences about examinees’cognitive skills in algebraon the SAT. Journal of Technology，Learning，and Assessment，6(6).

Gierl，M. J.，Zheng，Y.，＆ Cui，Y. (2008). Using the attribute hierarchy method to identify and interpret the cognitive skills that produce group differences. Journal of Educational Measurement，45，65 -89.

Junker，B. W.，＆ Sijtsma，K. (2001). Cognitive assessment models with few assumptions，and connections with nonparametric item response theory. Applied Psychological Measurement，25(3)，258 -272.

Leighton，J. P. (2004). Avoiding misconceptions，misuse，and missed opportunities:The collection of verbal reports in educational achievement testing. Educational Measurement:Issues and Practice，23，6 -15.

Leighton，J.P.，＆ Gierl，M.J.(2007a).Defining and evaluating models of cognition used in educational measurement to make inferences about examinees’thinking processes. Educational Measurement:Issues and Practice，26，3 -16.

Leighton，J. P.，＆ Gierl，M. J. (2007b). Verbal reports as data for cognitive diagnostic assessment.In J.P.Leighton ＆ M.J.Gierl(Eds.)，Cognitive diagnostic assessment for education:Theory and applications(pp. 146 - 172). Cambridge，UK:Cambridge University Press.

Leighton，J.P.，Gierl，M.J.，＆ Hunka，S.(2004).The attribute hierarchy model:An approach for integrating cognitive theory with assessment practice. Journal of Educational Measurement，41，205 -236.

Maris，E. (1999). Estimating multiple classification latent class models.Psychometrika，64(2)，187 -212.

Tatsuoka，K.(1985). A probabilistic model for diagnosing misconceptions in the pattern classification approach. Journal of Educational Statistics，10，55 -73.