用Delta 法估计误差相关测验合成信度的置信区间:以FAD 为例*

叶宝娟，杨 强

(1.江西师范大学心理学院，江西省心理与认知科学重点实验室，南昌330022;2.江西师范大学教育学院，南昌330022)

1 引言

信度是衡量测验质量的重要指标，α 系数是目前最常用的评价测验信度的指标，但在题目测量误差(简称误差)相关的情况下往往会高估测验信度，这种高估的偏差可以高达两成(Green ＆ Yang，2009;Revelle ＆ Zinbarg，2009;Sijtsma，2009;温忠麟，叶宝娟，2011)。虽然在大多数的研究中，假定误差不相关是合理的，但在一些情况下误差之间会相关，如速度测验、刺激材料相同的测验题目、测验分数有瞬间误差(transient error，被试对测验有某种特殊的感情、态度等会影响其测验分数而产生的误差)等等(Green，2003;Green ＆ Hershberger，2000;Green ＆Yang，2009;Steinberg，2001)。在心理与教育中，经常使用加入反向题目(negatively worded item)的单维测验，比如感恩测验、自尊测验、自我概念测验、家庭功能测验等，这类测验正向题、反向题的误差也可能存在相关。在以往的研究中，平衡使用正向题和反向题的单维测验通常当作单维分析，但越来越多的研究者发现这样的测验存在项目表述方法效应(method effect)，即由项目表述引起的变异，应当加以控制(DiStefano ＆ Motl，2009;Marsh，Scalas，＆ Nagengast，2010;Vautier ＆ Pohl，2009;Ye，2009)。检验测验是否存在方法效应的一种做法是相关特质相关特性(Correlated - Trait Correlated - Uniqueness，CTCU)模型，把项目表述效应当作影响因子结构的噪音，通过限制所有的正向题或反向题的测量误差相关，将项目表述效应分离。在误差相关的情况下，使用α 系数估计测验信度是不合适的，利用验证性因子模型，用合成信度(composite reliability)可以比较准确地估计测验信度(Bentler，2009;温忠麟，叶宝娟，2011;Yang ＆ Green，2010)。

许多研究者提倡用置信区间来报告参数估计结果(例如，Bonett，2010;Maydeu -Olivares，Coffman，＆Hartmann，2007;Woods，2007;叶宝娟，温忠麟，2011，2012a;Zou，2007)。如果可接受的信度包含在测验信度的置信区间中，则还不能判断此测验的信度是否可以接受(叶宝娟，温忠麟，2011)。

对于误差不相关的情形，有三种方法或途径估计合成信度的置信区间:Bootstrap 法、Delta 法和直接引用SEM 软件(如LISREL)输出的标准误进行计算(叶宝娟，温忠麟，2011)。Bootstrap 法得到的结果是实证结果，最为可信，但需要数据模拟技术，非常麻烦。Delta 法是一种近似计算，可在SEM 软件中添加额外参数编程，根据结果文件输出，进行简单计算即可得到标准误，比Bootstrap 法简单。SEM 软件添加额外参数估计合成信度时，结果文件会直接给出其标准误，此法比Bootstrap 法和Delta 法都要简单。叶宝娟和温忠麟(2011)的模拟研究显示，Delta 法的标准误与Bootstrap 法的标准误差异很小，而LISREL 输出的标准误远远大于Bootstrap 法的标准误，推荐用Delta 法估计合成信度的置信区间，但不能直接用LISREL 输出的标准误来计算。用Mplus 容易计算Delta 法估计的合成信度的置信区间，若用LISREL 需要将有关的结果代入Delta 法公式进行计算。

对于误差相关的情形，目前尚未见到用Delta法计算合成信度标准误公式，本文将进行这方面的工作。简单介绍了单维测验合成信度;介绍了如何用Delta 法估计误差不相关时单维测验合成信度置信区间;对误差相关的情形，推导出用Delta 法计算合成信度标准误的公式，据此可以计算合成信度置信区间;用中文版FAD 分测验“总的功能”为例说明了如何用本文推导的公式进行计算。

2 单维测验合成信度

设一个单维测验由p 个题目x1，x2，…，xp组成，测量了因子ξ，δ1，δ2，…，δp分别为x1，x2，…，xp的误差，则有

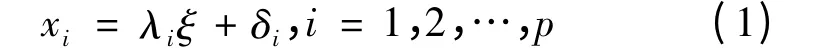
其中，λi表示题目i 在因子ξ 上的负荷。如果整份测验的分数相加有意义，整份测验分数X = x1+ x2+ … + xp的合成信度为(Yang ＆ Green，2010)

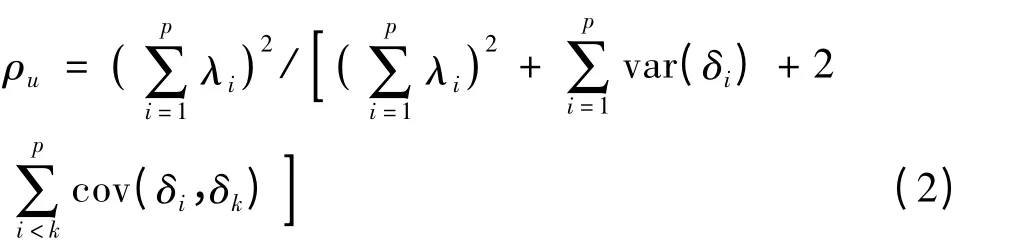
其中，cov(δi，δk)表示误差δi和δk之间的协方差。当误差之间不相关时，cov(δi，δk)= 0 ，则公式(2)变为

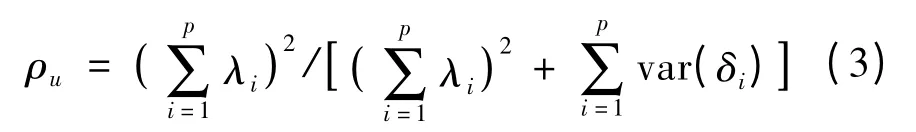
公式(3)是公式(2)的特例。很容易看出，如果误差存在相关，但仍用公式(3)计算合成信度是不准确的。如果题目的误差存在正相关，忽略误差相关计算的合成信度可能高估测验信度。

3 用Delta 法估计误差不相关单维测验合成信度的置信区间

近年来，许多研究用Delta 法估计参数的置信区间(例如，Laenen，Alonso，Molenberghs，＆ Vangeneugden，2009a，2009b;Raykov，2011;Raykov ＆ Penev，2009，2010)。Raykov(2002)最先将Delta 法用于合成信度的区间估计中，在误差不相关的条件下，他推导出估计单维测验合成信度的标准误公式为

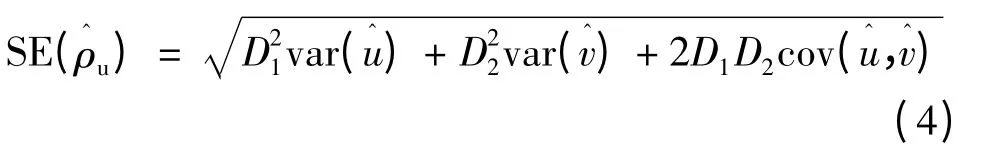
其中，u 是标准化因子负荷之和，u^是其估计，v 是误差方差之和，是其估计:

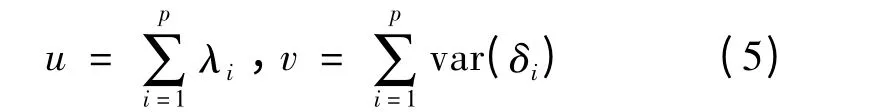
D1和D2由下面公式计算得到:

如果误差相关，用公式(4)估计的合成信度的标准误可能不准确，此时需要推导新的公式。

4 用Delta 法计算一般的单维测验合成信度置信区间

Raykov(2002)用Delta 法推导公式(4)的时候，是从公式(3)出发的。在误差相关的情形，要从公式(2)出发。设

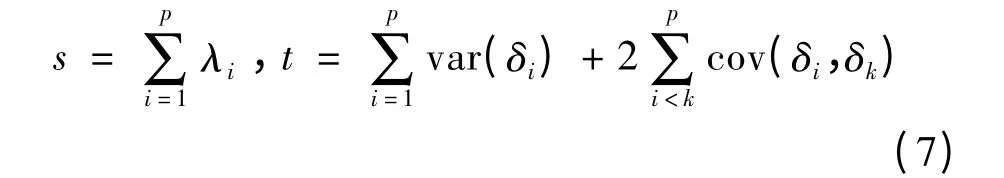
则(2)式变为:

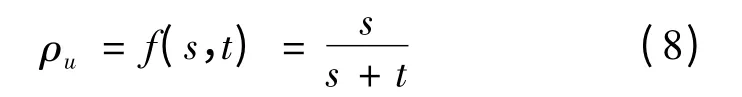
对上述公式应用Delta 法(叶宝娟，温忠麟，2012b)，可以推导出误差相关单维测验合成信度的标准误为:

其中，D3和D4为:

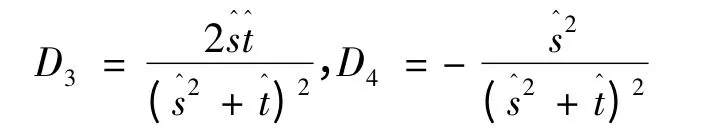
测验合成信度的置信度为1 - α 的置信区间为:

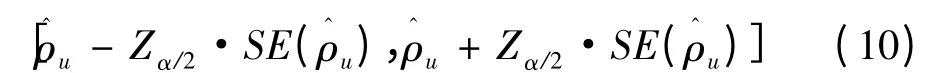
其中，Zα/2是标准正态分布的双侧α 分位点。公式(10)就是Delta 法得到的置信区间，半径为Zα/2·SE()，表示信度估计的误差范围。区间长度越短(即标准误越小)，估计的信度精确度越高，反之，精确度越低。

5 用Delta 法估计合成信度的置信区间示例

下面用一个例子说明如何用本文推导的公式计算误差相关的单维测验合成信度的置信区间。

家庭是个体成长和社会化的重要场所。家庭功能(family functioning)是衡量家庭系统运行状况的重要标志，会对家庭成员心理发展产生很大影响。家庭实现其功能的过程越顺畅，家庭成员的身心健康状况就越好，反之，则容易导致家庭成员出现各种心理问题以及行为问题。

最常用的评价家庭功能的工具之一是家庭功能评价测验(简称FAD)，是依据Mcmaster 的家庭功能模式编制的家庭功能测验(第三次修订版)，中文版由刘培毅、何慕陶(1999)进行翻译和修订，有7 个分测验，共60 个项目，25 个正向题，35 个反向题。虽然测验中包含反向题，但以往的研究者没有研究此测验是否存在方法效应，直接使用α 系数估计测验信度。如果存在方法效应，α 系数失去了参考价值。本例将研究FAD 分测验“总的功能”，在探讨其结构的基础上，演示如何比较准确的计算其合成信度及其置信区间。

5.1 被试

采用整群随机抽样，选取某地区六所初级中学(三所城市普通中学，三所乡镇普通中学)的600 名青少年(平均年龄为14.54 岁，SD=0.86)作为调查对象。其中，男生283 人，女生317 人，初一216 人，初二197 人，初三187 人;父亲和母亲没有固定工作者分别为15.2%和40.1%。父亲与母亲的受教育水平为“未受过正规教育或小学”者分别为15.8%和34.6%，“初中”水平者分别为52.0%和49.0%，“高中/职高”水平者分别为22.4%和12.7%，“大学专科/本科及以上”者为9.8%和3.7%。这与国家统计局公布的第六次全国人口普查数据相应群体受教育水平的全国平均状况以及本调查所在地区的平均状况均非常接近。

5.2 工具

采用FAD 分测验“总的功能”，共12 题，其中第1、3、5、7、9、11 为反向题，2、4、6、8、10、12 为正向题，采用4 级评分制，其评分为:很像我家=1、像我家=2、不像我家=3、完全不像我家=4。将6 个反向题反向计分。

5.3 程序

在征得学校领导和青少年本人的知情同意后，以班级为单位进行团体施测。主试为经过严格培训的心理学研究生。要求被试根据指导语要求认真、独立作答。被试完成全部问卷约需5 分钟，所有问卷当场回收。

5.4 结果分析

为分离项目表述效应，按照Tomás 和Oliver(1999)的建议，本研究构建7 个理论模型。其中，模型M1认为分测验的结构是单维的，即只有一个因子。而M2、M3和M4均为相关特质相关特性模型(CTCU)，它们在一个因子的基础上，假定存在正向题的测量误差相关(M2)或反向题的测量误差相关(M3)或两者同时存在(M4)。而M5、M6和M7为相关特质相关方法模型(CTCM)，即在一个因子的基础上分别假定存在一个反向题项目表述效应因子(M6)或正向题项目表述效应因子(M7)，或两者同时存在(M5)。接下来从拟合指数、模型的负荷两方面来比较7 个竞争模型。

模型M4没有收敛，因此未将其列入比较之列。由表1 可知，单因素模型M1拟合最差，χ2/df 最大，RMSEA 大于临界值0.08(温忠麟，侯杰泰，Marsh，2004);考虑项目表述方法效应的模型均好于模型M1，其中，模型M2和模型M5拟合很好，χ2/df，SRMR很小，模型M3、M6和M7居中，拟合也不错。由此可见，与M1相比，考虑项目表述效应的模型拟合更好，并且模型更简约。

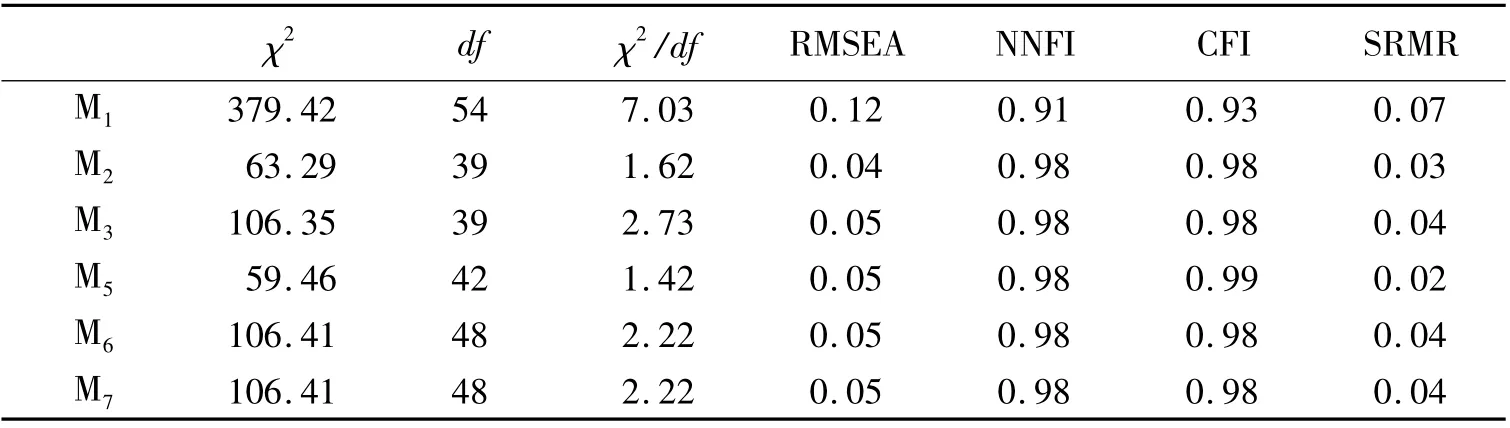
表1 竞争模型的拟合指数比较

温忠麟等(2004)认为，评估模型的优劣，除了要考虑拟合指标是否达到临界值，还要考察参数估计值的意义以及模型的可解释性。如表2 所示，在模型M5中，第11 题在方法因子的负荷为负值，这不太合理，同时分离出方法效应后，第5 题在总的功能上的负荷小于0.3，此题没有很好的测量总的功能，因此，模型M5不好;分离出方法效应后，在模型M2、M6、M7中，第1 和第5 题的负荷小于0.3，第5 题在总的功能上的负荷尤其低，这说明第1 和第5 题没有很好的测量总的功能，因此，模型M2、M6、M7不好;在模型M1中，第5 题在总的功能上的负荷小于0.3，此题没有很好的测量总的功能，因此模型M1不好;相比之下，在模型M3中，除第5 题外，各题的负荷均在0.4 之上，第5 题的负荷也高于在其它模型中的负荷，所有题目都较好的测量了总的功能，因此，相对于其它模型来说，模型M3好。

实施最严格的耕地保护制度。全省耕地保有量1.14亿亩，划定永久基本农田9587万亩，连续18年实现耕地占补平衡，保障粮食生产能力稳步提升。建立生态红线管理和生态补偿制度，对重要生态区域实施红线管理，对生态公益林、重要湿地和海域海岛保护给予生态补偿。建立自然保护地管理制度。在资源集中、区位重要、特色鲜明区域，建立各类省级以上自然保护区45处、地质矿山公园67处、森林公园119处、湿地公园204处、海洋公园12处，典型自然生态系统和生物多样性得到有效保护。持续推进矿产资源整顿规范，取缔关闭非法采矿和一批露天开采矿山，建成国家级绿色矿山37处，数量居全国第二位。

综合拟合指数、负荷方面信息，我们认为反向表述CTCU 模型M3是对总的功能结构的最好解释，即中文版FAD 总的功能分测验是单维结构，所有题目都测量了总的功能一个因子，反向题的测量误差相关。此外，对反向题项目表述效应进行统计控制后，此分测验的单维结构更好。

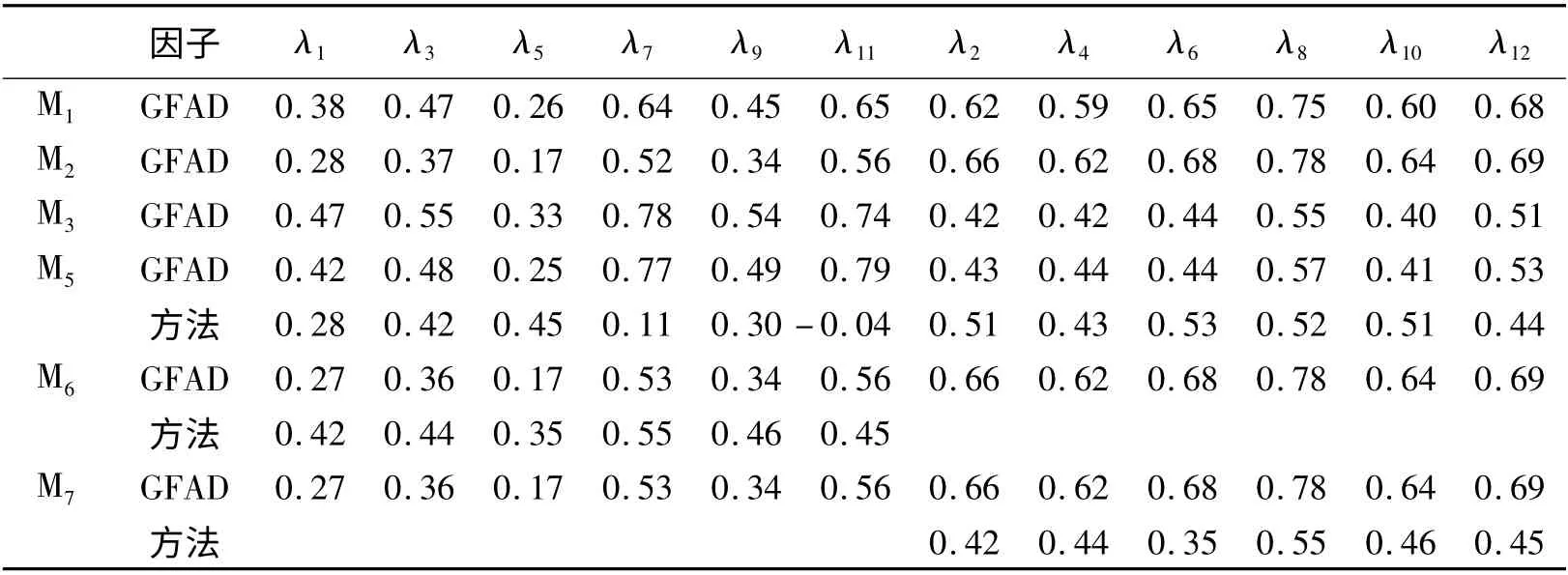
表2 竞争模型的负荷比较

接下来计算总的功能的信度，附录1 是计算这份测验模型M3的合成信度的LISREL 程序，并且可得到用公式(9)计算置信区间所需要的参数。这个程序与普通的CFA 程序差不多，仅多了几个额外参数。LISREL 的输出结果可以给出公式(2)中的合成信度的点估计值，以及公式(9)中的所有参数(但D3和D4需要计算)将LISREL 的输出结果代入公式(9)容易求得合成信度的标准误，进而用公式(10)计算其置信区间。本例合成信度的点估计值为0.76，合成信度的标准误为0.02，合成信度95%的置信区间为(0.72，0.80)。

为了进一步验证用Delta 法得到的置信区间的精确度，在LISREL 中用Bootstrap 法抽样1000 次，得到合成信度的标准误为0.02(可以看作真值，参见叶宝娟，温忠麟，2011)，因而95%的置信区间为(0.72，0.80)，与用Delta 法得到的置信区间(0.72，0.80)相同，说明用Delta 法估计的结果相当精确。

如果此例按误差不相关的公式(3)计算合成信度，用公式(4)计算标准误，合成信度的点估计值为0.85(高 估 了0. 09)。标 准 误 为0. 01(低 估 了0.01)，95%的置信区间为(0. 83，0. 87)，与Bootstrap 法得到置信区间(0.72，0.80)差别很大，信度下限相差了0.11。本例α 系数点估计值为0.86(高估了0.10)，用Bonett(2010)的方法计算其置信区间为(0.84，0.88)，信度下限相差0.12。

6 结论和讨论

估计测验的信度是进行数据分析的必须前提和关键性步骤(Biemer，Christ，＆ Wiesen，2009;Vangeneugden et al.，2010)。如果测验信度估计不准确，可能会高估或低估变量间的真实关系，直接影响基于信度基础上所做的统计分析的结果(Lachin，2004;Laenen et al.，2009a)。

在一些情况下测验误差之间会相关，此时，最常用的评价测验信度指标α 系数往往会高估测验信度，而用合成信度可以较好的评价此种情况下测验信度。测验的合成信度是一个未知的总体参数，实证研究中需要用样本的合成信度来估计。同其它参数的点估计一样，样本的合成信度会围绕总体的合成信度波动。用合成信度的置信区间来评价测验的信度，尤其是当样本的点估计值在可接受的信度水平附近时，可对测验的质量做出更为客观的评价。

在实证研究中，如果用速度测验、刺激材料相同的测验题目或测验分数有瞬间误差及测验有正向题、反向题时，应当检查测验题目的误差是否相关。如果相关，不能用α 系数估计信度，也不能用误差不相关的合成信度公式，而应该用误差相关的合成信度公式及标准误公式计算测验的合成信度及其置信区间，才能比较准确地估计测验信度。本文的例子已经充分说明了这一点。

在FAD 分测验“总的功能”中，反向题存在项目表述效应，导致反向题的误差相关，分离出项目表述效应的单维模型M3能较好地解释测验的结构。建议在使用该测验时，考虑此测验的方法效应，建立反向题误差相关的CFA 模型估计测验的信度及其置信区间。

Mplus 软件的高版本(如6.0 以上)用Delta 法计算合成信度的标准误(Muthén ＆ Muthén，2010)，并可以直接输出合成信度的置信区间，与本文用Delta 法求得的一样(计算误差除外)。附录1 给出了用Mplus6.11 求本文例子合成信度的点估计值及其置信区间的程序。在程序中OUTPUT 部分添加CINTERVAL 命令可以直接得到合成信度的置信区间。附录1 的程序可以直接得到合成信度的点估计值、Delta 法的标准误，以及相应的合成信度置信区间。如果读者使用Mplus 软件，可以套用附录1 的程序进行计算。

刘培毅，何慕陶. (1999). 家庭功能评定. 见 汪向东等. (主编).心理卫生评定量表手册(增订版)(pp.149 -150).北京:中国心理卫生杂志出版社.

温忠麟，侯杰泰，Marsh.(2004). 结构方程模型检验:拟合指数与卡方准则.心理学报，36(2)，186 -194.

温忠麟，叶宝娟.(2011).测验信度估计:从α 系数到内部一致性信度.心理学报，43(7)，821 -823.

叶宝娟，温忠麟. (2011). 单维测验合成信度三种区间估计的比较.心理学报，43(4)，453 -461.

叶宝娟，温忠麟.(2012a).测验同质性系数及其区间估计.心理学报，44(12)，1687 -1694.

叶宝娟，温忠麟. (2012b). 用Delta 法估计多维测验合成信度的置信区间.心理科学，35(5)，1213 -1217.

Bentler，P. M. (2009). Alpha，dimension - free，and model -based internal consistency reliability. Psychometrika，74，137-143.

Biemer，P.P.，Christ，S.L.，＆ Wiesen，C.A.(2009).A general approach for estimating scale score reliability for panel survey data.Psychological Methods，14，400 -412.

Bonett，D.G.(2010). Varying coefficient meta -analytic methods for alpha reliability. Psychological Methods，15，368 -385.

DiStefano，C.，＆ Motl，R. W. (2009). Personality correlates of method effects due to negatively worded items on the Rosenberg Self - Esteem scale. Personality and Individual Differences，46，309 -313.

Green，S. B. (2003). A coefficient alpha for test - retest data.Psychological Methods，8，88 -101.

Green，S.B.，＆ Hershberger，S. L. (2000). Correlated errors in true score models and their effect on coefficient alpha.Structural Equation Modeling，7，251 -270.

Green，S.B.，＆ Yang，Y.(2009).Commentary on coefficient alpha:A cautionary tale.Psychometrika，74，121 -135.

Lachin，J. M. (2004). The role of measurement reliability in clinical trials.Clinical Trials，1，553 -566.

Laenen，A.，Alonso，A.，Molenberghs，G.，＆ Vangeneugden，T.(2009a).A family of measures to evaluate scale reliability in a longitudinal setting.Journal of the Royal Statistical Society，172，237 -253.

Laenen，A.，Alonso，A.，Molenberghs，G.，＆ Vangeneugden，T.(2009b). Reliability of a longitudinal sequence of scale ratings.Psychometrika，74，49 -64.

Marsh，H.W.，Scalas，L. F.，＆ Nagengast，B. (2010). Longitudinal tests of competing factor structures for the Rosenberg Self-Esteem scale:Traits，ephemeral artifacts，and stable response styles.Psychological Assessment，22，366 -381.

Maydeu - Olivares，A.，Coffman，D. L.，＆ Hartmann，W. M.(2007).Asymptotically distribution free(ADF)interval estimation of coefficient alpha. Psychological Methods，12，157 -176.

Muthén，L.K.，＆ Muthén，B. O. (2010). Mplus user’s guide(6th ed.).Los Angeles:Muthén ＆ Muthén.

Raykov，T. (2002). Analytic estimation of standard error and confidence interval for scale reliability.Multivariate Behavioral Research，37，89 -103.

Raykov，T.(2011). Intraclass correlation coefficients in hierarchical designs:Evaluation using latent variable modeling.Structural Equation Modeling，18，73 -90.

Raykov，T.，＆ Penev，S.(2009).Estimation of maximal reliability for multiple - component instruments in multilevel designs.British Journal of Mathematical and Statistical Psychology，62，129 -142.

Raykov，T.，＆ Penev，S.(2010).Evaluation of reliability coefficients for two - level models via latent variable analysis.Structural Equation Modeling，17，629 -641.

Revelle，W.，＆ Zinbarg，R. (2009). Coefficients alpha，beta，omega and the glb:Comments on Sijtsma. Psychometrika，74，145 -154.

Sijtsma，K.(2009).Reliability beyond theory and into practice.Psychometrika，74，169 -173.

Steinberg，L. (2001). The consequences of pairing questions:Context effects in personality measurement.Journal of Personality and Social Psychology，81，332 -342.

Tomás，J.M.，＆ Oliver，A. (1999). Rosenberg’s self -esteem scale:Two factors or method effects.Structural Equation Modeling，6，84 -98.

Vangeneugden，T.，Molenberghs，G.，Laenen，A.，Geys，H.，Beunckens，C.，＆ Sotto，C.(2010).Marginal correlation in longitudinal binary data based on generalized linear mixed models.Communications in Statistics - Theory and Methods，39，3540 -3557.

Vautier，S.，＆ Pohl，S.(2009).Do balance scales assess bipolar constructs?The case of the STAI scales.Psychological Assessment，21，187 -193.

Yang，Y.，＆ Green，S.B.(2010).A note on structural equation modeling estimates of reliability. Structural Equation Modeling，17，66 -81.

Ye，S.(2009).Factor structure of the General Health Questionnaire(GHQ - 12):The role of wording effects. Personality and Individual Differences，46，197 -201.

Zou，G. Y. (2007). Towards using confidence intervals to compare correlations.Psychological Methods，12，399 -413.

附录1 计算单维测验的合成信度的Mplus 程序

注释:合成信度的点估计值及用Delta 法计算的合成信度的标准误，对应于Mplus 输出结果中的“MODEL RESULTS”部分中的“New/Additional Parameters”H4 的参数估计值及其标准误，其值为0.76 和0.01。合成信度的95%置信区间的下限和上限，对应于Mplus 输出结果中的“CONFIDENCE INTERVALS OF MODEL RESULTS”部分中的“New/Additional Parameters”H4的“Lower 2.5%”和“Upper 2.5%”的值，其值为0.72 和0.80。