字母混淆矩阵的多维尺度分析*

赵广平

(1.复旦大学社会发展与公共政策学院，上海200062;2.闽南师范大学教育系，漳州363000)

多维尺度分析法(multidimensional scaling，简称MDS)是一种多变量的探索性数据分析技术，能够推断出被试知觉空间的维度。该技术将大型数据压缩到低维空间，形成直观的空间地图。以空间中的“点”表示对象，点间距表示对象的相似度或相异性。MDS 处理的原始数据是一种对刺激或对象间的整体相似性和相异性进行度量的数据，并不严格要求数据的正态分布假设(Jaworska ＆ Chupetlovska-Anastasova，2009)具有很强的数据适应性。

1 MDS 原理简介

根据原始数据的计量水平，可把MDS 分为计量(metric)和非计量(non -metric)的。计量MDS 技术假定对象间的相似性矩阵数据呈现了矩阵的属性，就像地图上测得的距离一样。人们能够通过什么方法知道地图上两个城市A 与B 之间的距离呢?一种方法是通过量尺来测量;另一种方法也可以通过2 维空间坐标系确定两城坐标A(Xa，Ya)和B(Xb，Yb)来计算其距离dab，常用的欧式距离就定义为:

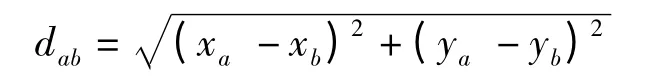
反过来，如果人们知道城市间的距离，是否可能根据距离画出地图呢?Torgerson 首次解决了该问题。算法涉及线性代数的知识，距离采用欧式距离，这是一种构建MDS 空间的优先选择的距离算法。当然，还有非欧距离，这受到具体研究问题的约束(Torgerson，1952)。

非计量MDS 技术是由Shepard 和Kruskal 发展起来的，主要运用对象间的排序信息构建空间，通过相似性的单调转换，得到等级相似性(Shepard，1980)。基本步骤是:首先找到一个随机匹配点(如通过正态分布进行取样);接着计算点间距，再进一步找到描述相似性的最佳数据;紧接着根据最优数据和估算距离之间的应力系数，找到新的匹配点，并将所得应力系数和某标准比较。如果应力值达到标准则退出算法，否则返回继续优化。非计量MDS 算法的核心是一个双重优化的过程，根据相似性的最优单调转换，最优排列对象点(Shepard，1962)。

由于计量的MDS 空间算法涉及原始数据提供的所有信息，因而其保存了对象间相似性或距离的全部信息，是一种很好的数据处理技术。但它对数据的计量水平有很高要求，这限制了其现实应用的适应性。相比之下，由于对原始数据计量水平要求较低，非计量MDS 只假定对象间的顺序信息是有意义的，点间距的等级只能尽可能反映对象间相似性或距离的部分信息。正因为此，非计量MDS 技术对很多测量方法和数据具有更大适应性。

下文在简述MDS 的应用规范基础上，对Mayzner(1965)关于模式识别的早期研究(字母辨别实验)进行再分析，主要是对25 个字母的混淆矩阵进行MDS 分析(Appelman ＆ Mayzner，1982;梁宁建，2003)，试图阐明和验证MDS 技术在认知心理学研究中的独特适用性和恰当性。

2 数据收集方法:直接和间接

对数据进行MDS 分析主要是寻找众多对象空间分布的过程，以测查对象的整体相似性和相异性程度，常被称为相似性或相异性推导。数据通常排列在一个平方矩阵(相似矩阵或距离矩阵)内。根据相似性数据收集的方式分为:直接方法和间接方法(Torgerson，1952;赵守盈，吕红云，2010)。下面分别简述。

2.1 直接方法

直接收集相似性数据的方法就是要求被试将数字相似性或相异性的度量值分配给每对刺激，也可以根据刺激的相似性或相异性对刺激进行等级排序。排序的方式有很多，比如两两比较排序法、一对多的比较排序法、偏序排序法和归类排序法等。直接等级评定的好处是:数据可以直接用于MDS 分析，并通过相似矩阵的平均值对每个被试进行个别分析(对被试的分析)和整体分析(对变量的分析)。其缺点是，当对象数量稍有增加时，总数据量就会猛增。

两两比较排序法。向被试呈现刺激的所有可能配对(总配对数是n(n-1)/2，n 是对象数量)，要求被试使用量表(如2 点或5 点量表)，数字越小表示对象间越相似，数字越大表示越不相似。据此规则比较排序每对刺激。该方法得到的相似性关系是对称的，但不对称的相似性关系也可能出现，比如混淆数据(见表1)，在SPSS 软件的MDS 程序中有不对称矩阵的命令选项。

一对多的比较和归类排序法。由Rao 提出，具体操作是:要求被试按照某标准从众多刺激中选出一个刺激作为比较刺激，再将比较刺激与其余刺激一一比较，再对挑选出的刺激进行相似性排序。重复该比较过程，直到所有的对象都有了自己的等级序数。当比较刺激与某些对象相比，难以或者无法给出排序值时，可以将其空缺。这叫一对多比较的偏序法(partial order)，该排序法允许缺失值的存在。另外，Rao 也提出另一种方法，即归类法。具体操作是:要求被试根据刺激的相似程度，把最相似的刺激归为一组，再根据组与组间的相似性对组进行归并，直到将所有刺激归为一大组，以两个刺激被归为同一组的次数作为相似性数据(Rao ＆ Katz，1971)。

2.2 间接方法

与直接方法相比，间接方法并不要求被试直接指定数值，主要通过其他的方法获得相似性矩阵(如相关矩阵和混淆矩阵等)。

心理学研究中广泛使用相关分析，当使用不同量尺测量同一被试或者根据某一标准匹配被试时，就能产生相关矩阵。有时很难发现相关矩阵的潜在结构，探索性和验证性因素分析都是研究相关矩阵结构的高级多元统计方法(Tucker - Drob ＆ Salthouse，2009;赵广平，曾天德，2009)。但它们主要建立在等距或等比测量的基础上，而MDS 技术对数据类型并没有严格限定，可以处理类别和顺序数据。其解决方案是根据刺激间的距离，将刺激标示在平面图上，这就可以直接观察数据的结构。与因素分析技术相比，MDS 分析还有另外的优势:MDS 分析可以分析那些刺激或对象的测量尺度、概念维度或刺激属性未知的变量，而因素分析则必须建立在测量尺度和概念维度已知的情况下。混淆数据是指被试对两刺激的混淆次数，即被试把某一对象刺激错误地判断为另一刺激的频次或频率，这也是MDS 分析的间接数据之一。

综上所述，直接和间接的方法都是为MDS 过程的数据输入服务的，最终都会产生相似矩阵。在实际研究中，直接方法要求被试直接判断客体对象的相似性或相异性，而间接方法并不需要如此，非常适合对以往经典研究文献汇报的间接数据进行二次分析。

下文以知觉领域的早期研究——Mayzner 的字母混淆实验为案例和数据来源(见表1)，研究混淆数据矩阵的MDS 分析过程，以探究MDS 在这一领域的适用性，更好地挖掘前人的研究数据。

3 字母混淆矩阵的MDS 分析

知觉的特征匹配理论认为，各种刺激在长时记忆系统中的形式，既不是模板(模板匹配理论)，也不是原型(原型理论)，而是刺激的基本特征和属性。比如字母“A”，其刺激特征就是两条线段和一个连接它们的短横线。在模式识别过程中，被试对呈现的刺激，首先要分析和抽取其特征或属性，再将抽取出来的特征或属性加以合并整合，最后整合后的刺激模式与长时记忆中存储的各模式比较。一旦外部刺激模式与大脑内部的刺激模式获得最佳匹配，模式就获得了识别。

3.1 研究假设

根据特征匹配理论可知:两个刺激的特征差别越大，被试越容易区分，而对于相似的刺激更容易发生混淆(Appelman ＆ Mayzner，1982)。

3.2 实验步骤

Mayzner 以25 个英文字母(不包括“Q”字母)为实验刺激，使用速视器，按照5 种呈现时间(12ms、14ms、16ms、18ms 和20ms)，逐个随机呈现字母刺激。要求被试完成125 次(25 字母×5 呈现时间)字母识别任务。

3.3 实验结果

从实验步骤可知，被试是把看到的一个字母刺激与记忆中储存的25 个字母进行一对多的比较，并据此做出反应的。这说明，该实验的混淆矩阵来自一对多的比较排序法。表1 数据是25 个字母两两混淆的频次。其左上角第1 行第2 列的数字“2”表示:当呈现字母“B”时(行字母)，所有被试把“B”错判为“A”(列字母)的频次是“2”。而被试把“A”错误判断为“B”的频次却是“10”(第2 行第1 列)，可知被试把“A”错判为“B”的次数并不等于把“B”错判为“A”的次数(“2 ≠10”)，矩阵为非对称矩阵。数据矩阵的对称性影响相似矩阵的算法，在MSD 的分析中是必须考虑的。

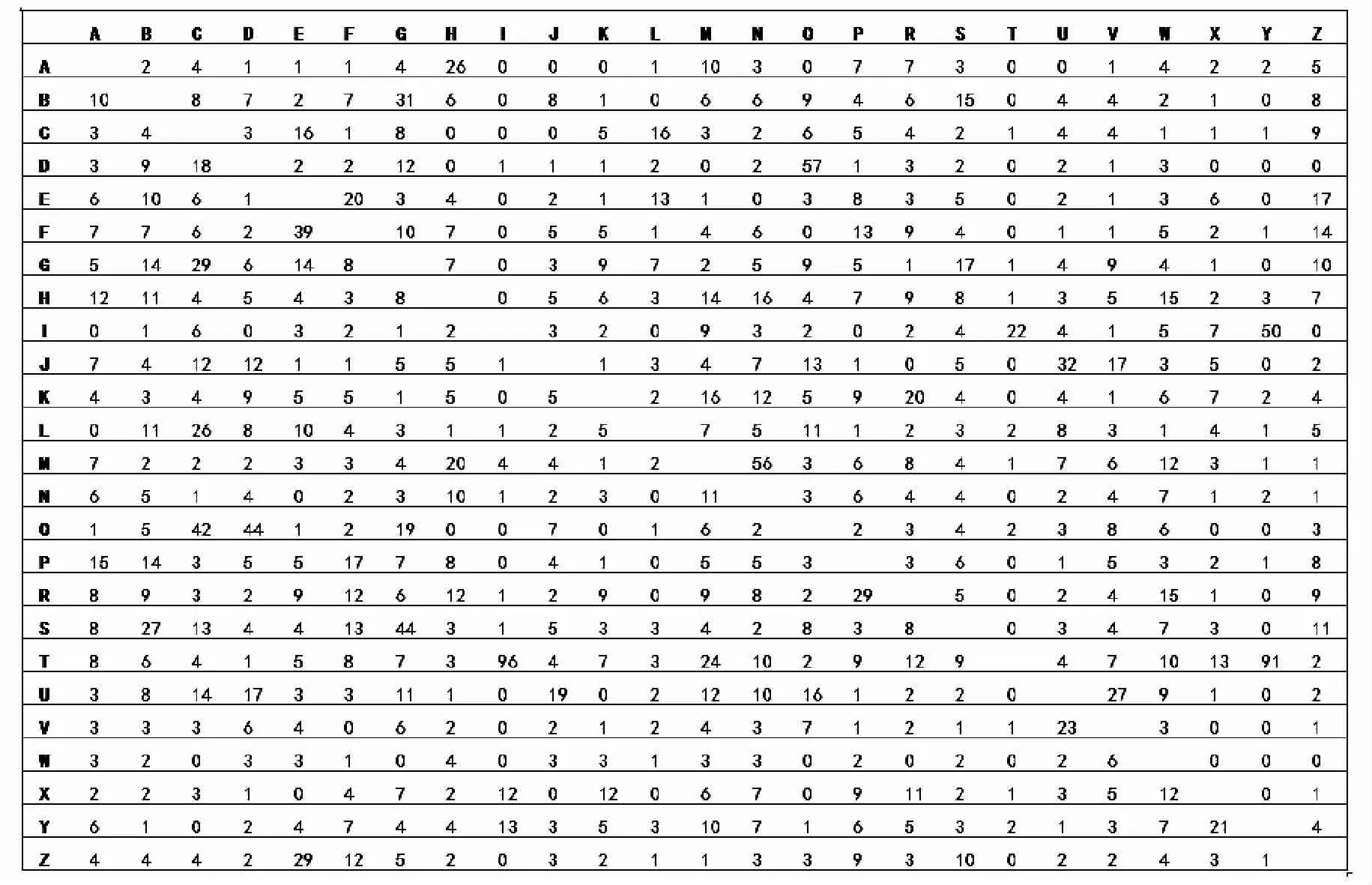
表1 25 个字母的混淆矩阵

3.4 数据处理与分析

使用SPSS19.0 完成数据转录、转换和处理工作。

原实验者对表1 数据做了初步统计分析:(1)通过直条图分析(横坐标为5 种呈现时间;纵坐标为字母正确识别次数)。结果发现，被试对字母正确识别的次数会随着呈现时间的增加而增多;(2)把每个字母的混淆频次与5 种呈现时间进行交叉统计。结果表明，具有相似特征的字母，被试更容易混淆，而特征差别较大的刺激不易混淆。

随着高级多元统计技术的发展，使用MDS 技术对Mayzner 的实验数据进行重新分析，发现数据处理结果虽与原实验者大体一致，但也挖掘到新的信息。从表1 可知，混淆矩阵中的最高频次达到了96，虽然频次属于非计量数据，但量尺全距足够大，可以近似采用计量MDS 分析;由于混淆矩阵是非对称阵，MDS 采用非对称距离矩阵算法;由于MDS 的3 维空间分布图并不直观，采用2 维空间分析。结果显示，MDS 的2 维空间分布图(见图1)把25 个字母分为四类。其决定系数(RSQ)为0.47;应力系数(Stress)为0.34。这两个指标都是数据处理的拟合指数，RSQ 表示欧氏距离模型解释实际数据方差的百分比;Stress 通常用于判断拟合度，值越低拟合越好，反之亦然。Kruskal 提供了应力系数值的使用准则(Jaworska ＆ Chupetlovska - Anastasova，2009)如表2 所示:

表2 应力大小和拟合程度的对应关系

根据表2 准则可知，对25 个字母的混淆矩阵进行MDS 分析的恰当性是保守的。这可能与原实验的被试量较少，或者刺激快速呈现导致被试判断干扰较大有关。也可能与该实验的任务操作有关:呈现刺激消失后，要求被试产生字母，这种任务操作容易受到很多因素的干扰。以上因素都会造成混淆矩阵数据具有很大随机误差或无关变异，因而对待该实验的结果需要谨慎。但也要注意，在MDS 文献中有很多不同的应力公式。Kruskal 准则只适用于计量MDS，实际应用中很容易被滥用，而且其值会随着维数的增加而降低。一般来说，2 维空间的应力值高于3 维空间。另外，应力系数的绝对值只是拟合程度的模糊指示。碎石图和Shepard 图也可以用来判断MDS 足够性的参考(Jaworska ＆ Chupetlovska-Anastasova，2009)，这里不再赘述。

图1 25 个字母的欧氏距离空间分布图

从图1 可知，MDS 分析结果与原实验结果相一致。原实验发现，C 和O、E 和F、N 和M、T 和I 等字母容易混淆;而G 和W、H 和I、F 和O、S 和T 等字母不易混淆。图1 显示，易混淆字母都被分配在同一空间，而不易混淆字母都在不同空间。比如，C 和O 都被分配在左上象限。MDS 以平面空间的形式呈现实验结果，较之原作者只呈现字母混淆频次的方式，显然直观得多。与原实验结果不相符的是字母对C 和S、V 和D。Mayzner 认为，C 和S 具有更加相似的特征而更易混淆，但图1 中C 却位于左上象限，而S 位于左下象限，且距离很大;Mayzner 认为V和D 的特征差别很大而不易混淆，但图1 中V 和D都在第二象限中，距离较近。

如果抽取图1 中同一象限字母群的共同特征，不难发现，除了字母的视觉特征相似性之外，被试书写字母的动作特征也很可能是一个不容忽略的影响因素。这一点是否涉及到具身认知(embodied cognition，Goldman ＆ de Vignemont，2009)等内容，需进一步研究。比如，右上象限的字母(W、T、Y、X、M、N和I)的共同特征是书写动作大多包含单调直线运动;左上象限(O、D、J、U、V、L 和C)则大多包含单调曲线或折线运动;左下象限(E、F、S、B、Z 和G)是交替的左右运动;右下象限(H、A、R、P 和K)是以一条竖线起笔向右书写一笔或两笔)。如果仅仅根据视觉特征的相似性分类，I、J 和L 可能更应该属于同一群组，但数据的信息却并非如此。

需要特殊说明的是，欧式空间中各个象限空间是连续的，不是绝对割裂的。有些字母虽然分属不同的空间象限中，但它们的距离并不很远，如果分布在数轴附近，也可以把这些字母进行单独归类。比如图1 中L、C 和G、还有F 和P 虽分属不同象限，但它们很显然具有视觉上的共同特征，也可归为一类。

3.5 讨论

混淆数据的优点是刺激的相似性判断建立在感知水平上，没有涉及太多的认知加工过程。通过以上分析可知，MDS 技术可以揭示非常基础的知觉层面的加工特点。要说明的是，以上数据分析是建立在应力系数比较高的基础上的，欧氏距离模型拟合不是最佳水平，进一步的研究需要收集大样本数据量，以及对实验设计进行更合理的调整。另一方面，混淆数据通常是不对称的，不能够进行个别数据分析，只能在整合所有被试结果的基础上进行整合分析。最后，MDS 分析发现的字母识别可能与书写动作有关，这一推断提示，Mayzner 的字母混淆实验可能要控制被试的左右利手特征，这种控制可能提高混淆矩阵的欧氏距离模型拟合程度。

4 结论

对Mayzner 字母混淆实验进行MDS 技术进行再分析的结果一定程度上支持知觉的特征匹配理论，这与原实验者的结论相一致。但也有新的发现:在快速呈现字母的情况下，被试对字母的辨别可能受到字母的书写动作特征的影响，这一发现的更深层机制需进一步研究。

以上研究表明，MDS 分析法对于认知心理研究中间接数据的处理是恰当的，可以更好地挖掘混淆数据的信息。由于这一特点，使用MDS 对心理学早期由于受到当时研究条件限制而无法进一步分析的研究数据进行再挖掘和再处理，可能是很有意义的。

梁宁建.(2003).当代认知心理学(p.73).上海教育出版社.

赵守盈，吕红云. (2010). 多维尺度分析技术的特点及几个基础问题.中国考试，(4)，13 -19.

赵广平，曾天德.(2009).心理测验中因素分析方法的比较.中国健康心理学杂志，11，50.

Appelman，I.B.，＆ Mayzner，M.S.(1982). Application of geometric models to letter recognition:Distance and density.Journal of Experimental Psychology:General，111(1)，60.

Goldman，A.，＆ de Vignemont，F. (2009). Is social cognition embodied?Trends in Cognitive Sciences，13(4)，154 -159.

Jaworska，N.，＆ Chupetlovska - Anastasova，A. (2009). A review of multidimensional scaling(MDS)and its utility in various psychological domains. Tutorials in Quantitative Methods for Psychology，5(1)，1 -10.

Kruskal，J. B. (1964). Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika，29(1)，1 -27.

Rao，V. R.，＆ Katz，R. (1971). Alternative multidimensional scaling methods for large stimulus sets. Journal of Marketing Research，488 -494.

Shepard，R.N.(1980). Multidimensional scaling，tree -fitting，and clustering.Science，210(4468)，390 -398.

Shepard，R.N.(1962).The analysis of proximities:Multidimensional scaling with an unknown distance function. Psychometrika，27(2)，125 -140.

Torgerson，W. S. (1952). Multidimensional scaling:Theory and method.Psychometrika，17(4)，401 -419.

Tucker-Drob，E.M.，＆ Salthouse，T. A. (2009). Methods and measures:Confirmatory factor analysis and multidimensional scaling for construct validation of cognitive abilities. International Journal of Behavioral Development，33(3)，277 -285.