滚仰式稳定平台质量不平衡分析

吴海龙,贾宏光,魏群,姜湖海,朱瑞飞

(1.中国科学院长春光学精密机械与物理研究所,130033,长春;2.中国科学院大学,100039,北京;3.西南技术物理研究所,610041,成都)



滚仰式稳定平台质量不平衡分析

吴海龙1,2,贾宏光1,魏群1,姜湖海3,朱瑞飞1

(1.中国科学院长春光学精密机械与物理研究所,130033,长春;2.中国科学院大学,100039,北京;3.西南技术物理研究所,610041,成都)

为了综合分析质量不平衡对滚仰稳定平台控制系统性能的影响,对某滚仰式稳定平台中的质量静不平衡和动不平衡问题进行了研究。首先解释了稳定平台质量不平衡的分类和产生原因,并采用动量矩定理建立了滚仰式稳定平台质量不平衡的数学模型;然后利用Simulink建立了某滚仰式稳定平台质量不平衡仿真模型,并通过不同的仿真研究了质量不平衡对滚仰式稳定系统的影响;最后通过实验对动不平衡进行了补偿研究。仿真结果表明:系统动不平衡力矩对系统响应超调量的影响可忽略,主要影响系统稳态误差;质量不平衡中,静不平衡是系统振荡和不稳定的主要原因。进行动不平衡补偿实验后,滚转框和俯仰框的稳态响应平均值分别提高1.34%和0.64%,均方差分别下降35.03%和55.19%。该研究结果对滚仰式稳定平台的质量不平衡分析和消除具有一定的参考意义。

质量不平衡;滚仰式稳定平台;不平衡力矩

在航空武器中,稳定平台广泛应用于扰动隔离、视轴稳定等方面[1-2]。与俯仰偏航式稳定平台相比,滚仰式稳定平台具有体积小、质量小、可实现360°滚转、±90°摆动的优点[3],这可极大地提高导弹的搜索和跟踪能力,因而滚仰式结构成为当今空空导弹导引头平台的理想选择。目前,该稳定结构形式已成功应用于美国AIM-9X空空导弹,而国内仍处在研究阶段,还没有应用此结构形式的导弹[4-6]。实际应用中,质量不平衡、摩擦和线绕阻力对滚仰式稳定平台的性能具有较大影响[7]。其中,质量不平衡会产生不平衡惯性力和振动,从而使框架的转动精度和可靠性降低;另一方面作为一种干扰,不平衡惯性力矩会影响滚仰式导引头框架的控制力矩,造成图形抖动,降低控制精度,进而降低导弹的制导精度。董安华等从实际试验中分析了质量不平衡对导引头的影响[8],指出质量不平衡导致某红外成像导弹在发射离梁瞬间目标丢失,打靶失败。因此,对滚仰式导引头中的不平衡力矩进行分析和研究是十分重要的。

目前,质量不平衡研究主要针对俯仰-偏航式稳定平台,滚仰式稳定平台的质量不平衡研究相关文献还未见。而且在研究俯仰偏航式结构时,基本采用了简化模型,在建模过程中忽略了质量动不平衡[9]。房建成等采用前馈补偿方法对三轴惯性稳定平台的不平衡力矩进行了抑制[10];于爽等提出一种惯性平台不平衡力矩的测试方法[11];朱华征等分析了导引头静不平衡力矩对其性能的影响,但并没有考虑质量动不平衡的影响[12];Maher等研究了框架间的耦合影响[13],但采用的仿真数据与实际数据存在较大差距,这导致研究结果与实际情况存在较大误差。因此,滚仰式稳定平台的质量不平衡问题仍有待深入研究。

结合实际系统,本文针对滚仰式稳定平台的质量不平衡问题分别建立了系统静不平衡和动不平衡模型,并分析了质量不平衡对系统的实际影响情况,以期为稳定平台的结构设计和装配及质量不平衡的分析和消除提供参考。

1 滚仰式稳定平台质量不平衡

根据滚仰式稳定平台质量不平衡的原因不同,可将其分为质量静不平衡和质量动不平衡。如图1所示,图1a为静平衡框架,其重心为G,其回转中心与重心重合,且垂直于纸面向外;图1b为在框架右侧增加了一质量块,此时其重心向右侧偏移,变为G′,并且不再与回转中心重合。当加速度a作用于框架时,重心偏移将会产生一附加干扰力矩,即静不平衡是因为框架的回转中心与其重心不重合造成的。在实际中,稳定平台的质量不平衡可能由机械结构设计、安装误差等造成。

(a)静平衡框架 (b)静不平衡框架图1 滚仰式稳定平台质量静不平衡示意图

滚仰式稳定平台的质量动不平衡示意图如图2所示。图2a中框架表示稳定平台的一个框架,G为其重心,该框架质量分布均匀,回转中心与其重心重合,在绕x轴转动过程中,转轴不会发生变化;图2b中分别在框架两侧增加了两个相同质量的质量块,在静止时其回转中心与其重心依然重合,但当图2b中框架绕x轴旋转时,由于其质量分布不均匀,将会产生附加力矩,使框架实际绕x′轴旋转,从而产生动不平衡力矩,即动不平衡是由于框架的质量沿其回转轴分布不对称造成的。

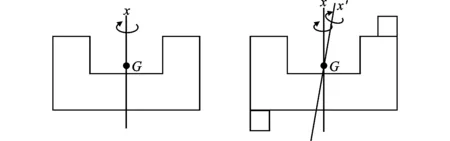
(a)动平衡框架 (b)动不平衡框架图2 滚仰式稳定平台质量动不平衡示意图

2 滚仰式稳定平台质量不平衡模型

2.1 静不平衡力矩公式

在研究静不平衡之前,先介绍导弹及导引头稳定平台中涉及的坐标系,如图3所示。

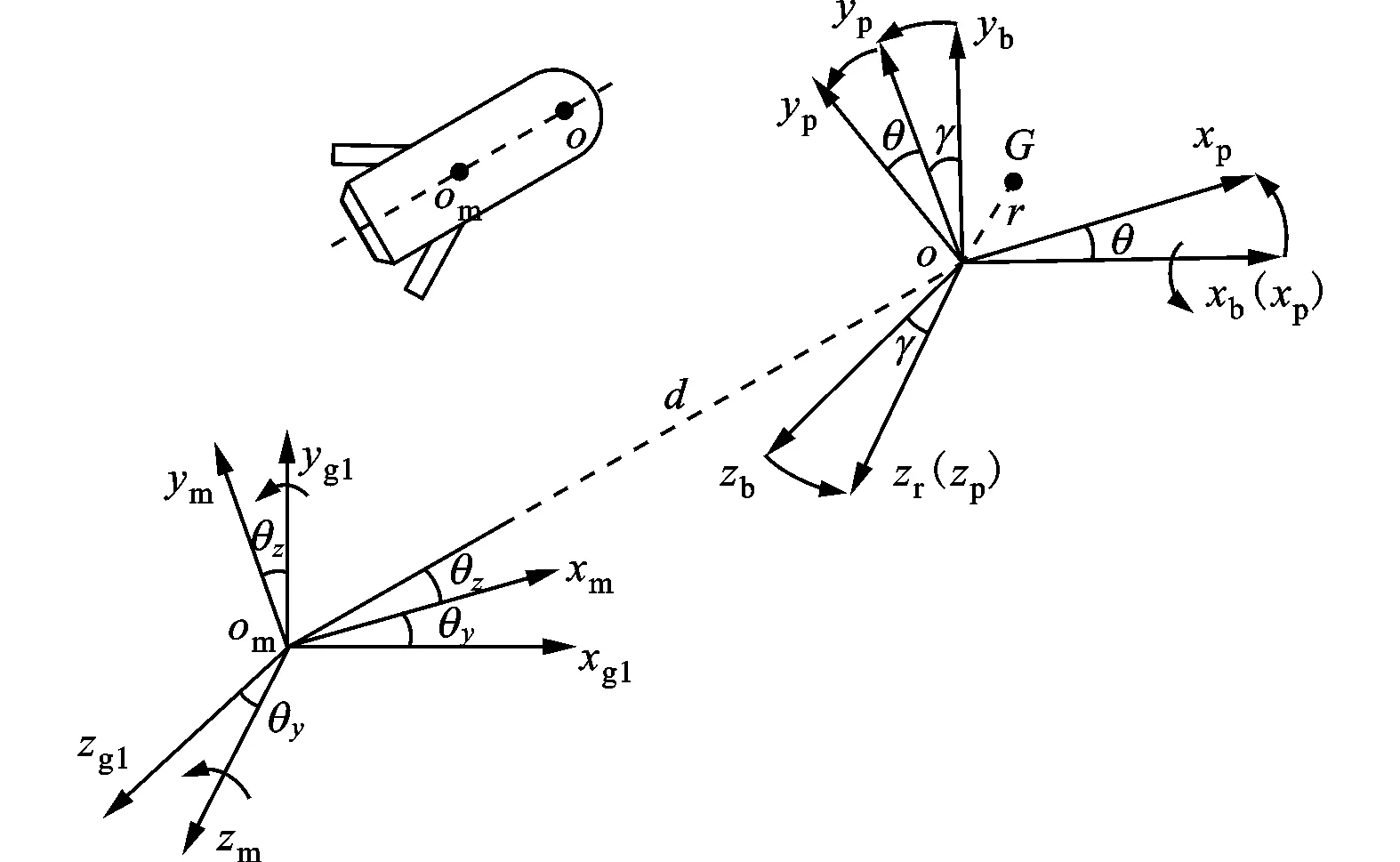
图3 弹体和导引头坐标变换示意图

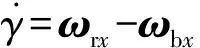
内框质心在内框坐标系下的投影为[rix,riy,riz]。

由图1可知,框架静不平衡力矩为过载加速度产生的力在偏心距下形成的力矩,可表示为

Tsit=mar

(1)

式中:m为框架的质量;a为框架的加速度;r为框架质心距框架回转中心的距离,即框架偏心距。

根据复合运动原理可知,动点o处加速度为

(2)

根据弹体与滚转框的坐标转换可知,滚转框的加速度为

(3)

根据滚转框与俯仰框的坐标转换可知,俯仰框的加速度为

(4)

根据式(1),可得俯仰框和滚转框的质量静不平衡力矩分别为

mp(rixcosθ-riysinθ)ax+

mp(rixsinθcosγ+riycosθsinγ)ay+

mp(rixsinθsinγ-riycosθcosγ)az

(5)

mr(roycosγ-rozsinγ)az-

mr(roysinγ+rozcosγ)ay

(6)

2.2 动不平衡动力矩公式

如图2所示,质量动不平衡是框架质量分布不均(即存在惯性积)造成的。因此,考虑内外框架的惯性积,定义滚转框和俯仰框的惯量阵为

(7)

(8)

由图3可知,滚框与弹体和滚框与俯仰框间的坐标转换关系分别为

(9)

(10)

将滚、仰两框架视为刚体,转动刚体动量矩定理为

(11)

式中:J为框架的惯量阵;ω为框架的速度阵。

考虑俯仰框存在质量动不平衡,根据式(10)可得俯仰框的动力学公式

(12)

式中:Tp为内框电机驱动力矩;Tditp1、Tditp2均为俯仰框质量动不平衡力矩,即

Tditp1=[(Jpx-Jpy)cos2θ+2dxysin2θ]ωrxωry-

(dxzsinθ+dyzcosθ)ωrxωpz

(13)

(14)

同理,可得考虑质量动不平衡的滚框动力学公式为

(15)

式中:Tr为外框电机驱动力矩,Tditr1、Tditr2、Tditr3均为滚转框质量动不平衡力矩,即

Jeqr=Jrx+Jpxcos2θ+Jpysin2θ-dxysin2θ

(16)

Tditr1=(Jry+Jpxsin2θ+Jpycos2θ+dxysin2θ-

Jrz-Jpz)ωryωrz

(17)

(18)

(19)

3 仿真研究

在研究分析滚仰式导引头内外框架质量不平衡时,本文忽略摩擦、线绕等干扰因素,采用某滚仰式稳定平台的设计参数进行仿真研究。根据式(5)、式(6)可以建立内、外框架的质量静不平衡Simulink仿真模型,根据式(12)、式(15)可以建立内外框架的质量动不平衡Simulink模型。图4为系统仿真原理图,ωinput是输入角速度指令,Gc是速度环控制器,Kg是陀螺标度因数,Tdit是内(外)框架的质量动不平衡力矩,Tsit是内(外)框架的质量静不平衡力矩,Je是负载转动惯量与电机转子在电机轴的等效转动惯量,ωout是输出角速度,r是内(外)框电机与框架间的传动比。Kt、Lm和Rm分别是内(外)框架电机的力矩系数、等效电感和电阻值。

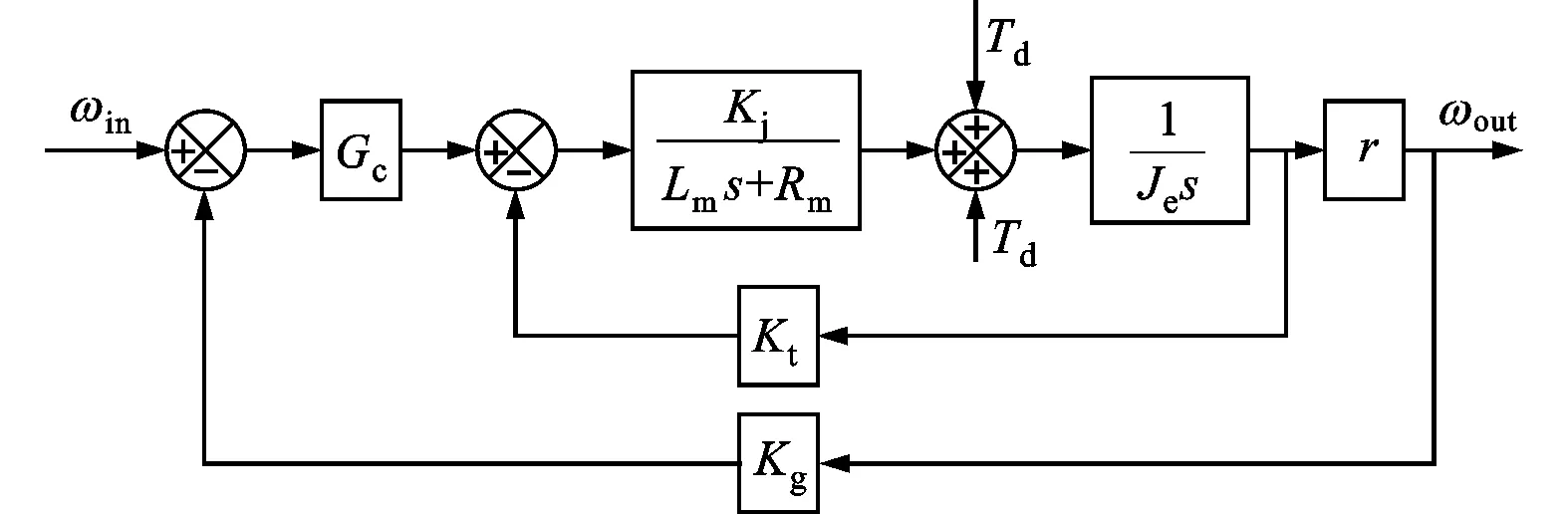
图4 滚仰式稳定平台质量不平衡仿真原理图

内框电机的力矩系数为0.034 N·m/A,转动惯量为2.5×10-6kg·m2,电感为1.1 mH,电枢电阻为7.9 Ω。内框电机的力矩系数为0.044 N·m/A,转动惯量为5.0×10-6kg·m2,电感为1.3 mH,电枢电阻为6.4 Ω。内外框速度反馈元件采用调谐陀螺,其标度系数为100 mV·s·(°)-1。外框电机与外框架间传动比为2.81,内框电机与内框间传动比为1。为使研究结果与实际相符,内外框架的转动惯量矩阵取值为某导引头的设计参数,即

(kg·m2)

(20)

(kg·m2)

(21)

在不考虑滚转和俯仰框架的质量动不平衡和静不平衡时,针对系统模型分别设计了内外框架的PI控制器,即

(22)

(23)

4 质量不平衡实验结果分析

本文采用的滚仰式导引头滚转框可以实现360°旋转,俯仰框可以±90°转动,即外框最大行程为360°,内框最大有效行程为180°。本文滚仰式稳定平台应用于近程空空格斗弹,该类型导弹从发射到击中目标,飞行时间小于60 s,故仿真时间均设置为60 s。

4.1 无质量不平衡时的系统响应

为了与考虑质量静不平衡和动不平衡影响时系统的响应作对比,首先研究了不存在质量不平衡时系统的响应。滚转框架和俯仰框架输入指令均为1 (°)/s,在不考虑质量动不平衡和静不平衡情况下,采用PI控制器,系统稳态响应分别如图5、图6所示。

图5 无质量不平衡时外框速度响应 图6 无质量不平衡时内框速度响应

在不考虑框架质量不平衡时,外框和内框超调量分别为9.6%和10.3%,系统无稳态误差,满足超调量不超过15%的指标要求。

4.2 质量静不平衡时的系统响应

取内外框架输入指令为1(°)/s,弹体扰动速度典型信号采用幅值为1(°)/s、频率为3 Hz的正弦信号。内、外框的控制器不变,在系统仿真模型中加入内、外框架的质量静不平衡,各方向弹体过载加速度取为最大值80g,内、外框架在各自坐标系中偏心距的投影均为0.001 m,弹体质心到导引头回转中心的距离取为1.5 m。在Simulink中进行仿真实验,得到存在质量静不平衡时外框架和内框架的质量静不平衡力矩和系统响应,分别如图7～图10所示。

图7 外框质量静不平衡力矩 图8 内框质量静不平衡力矩

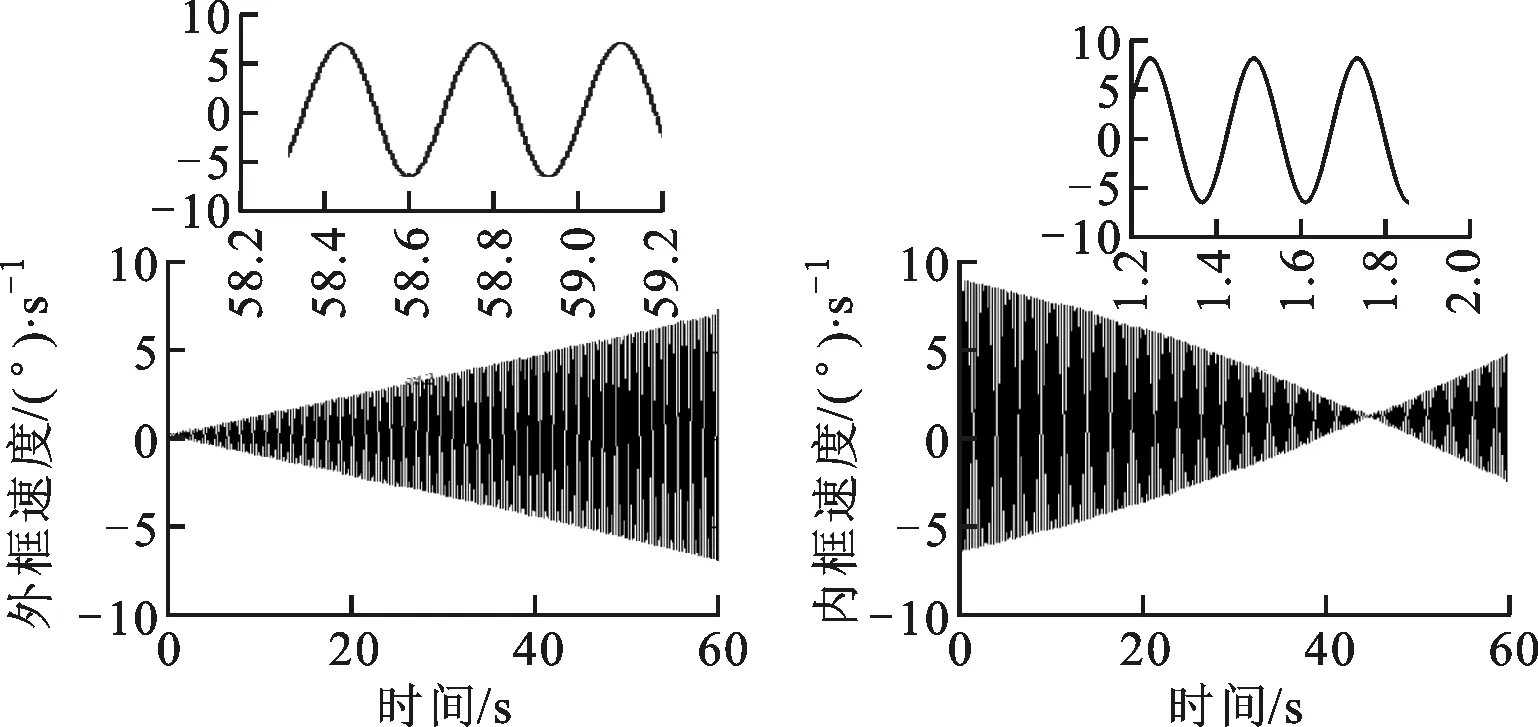
图9 存在静不平衡时外框阶跃响应 图10 存在静不平衡时内框阶跃响应

在考虑弹体扰动速度和80g过载加速度同时存在的情况下,内、外框架质量静不平衡力矩呈正弦式变化,周期与典型弹体扰动周期相同均为0.33 s;内、外框架在静不平衡力矩作用下系统振荡不稳定,振荡周期为0.33 s的正弦式变化,振荡幅值变化趋势与静不平衡力矩变化趋势一致。由此可知,静不平衡力矩会造成系统不稳定,导致导引头跟踪失效。

4.3 质量动不平衡时的系统响应

本文不仅研究了滚仰式稳定平台的静不平衡,同时研究了滚仰式稳定平台的动不平衡。同样取内外框架输入指令为1(°)/s,弹体扰动速度典型信号用幅值为1(°)/s、频率为3 Hz的正弦信号表示。采用Gp和Gr作为内框和外框的控制器,在系统仿真模型中加入内外框架的质量动不平衡,可得存在质量动不平衡时外框架和内框架的质量动不平衡力矩和系统响应,分别如图11～图14所示。

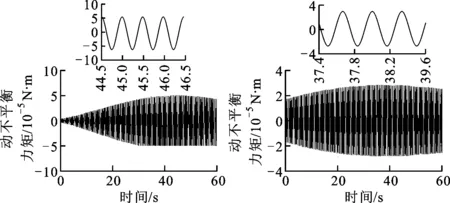
图11 外框质量动不平衡力矩 图12 内框质量动不平衡力矩

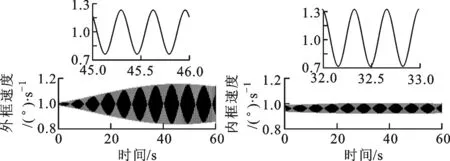
图13 存在动不平衡时外框阶跃响应 图14 存在动不平衡时内框阶跃响应

通过分析上述结果可知:动不平衡力矩也随时间呈正弦变化,且其周期与弹体扰动信号周期一致均为0.33 s;动不平衡力矩对系统超调量的影响较小,可忽略;与不考虑质量不平衡时的系统响应相比,在动不平衡力矩作用下,系统稳定但系统稳态误差影响变大,系统稳态误差呈正弦式变化,其变化周期为0.33 s,与扰动型号和动不平衡力矩扰动周期相同。综合可知,动不平衡力矩会降低控制精度,进而增大跟踪误差,从而造成跟踪图像抖动。

4.4 质量动不平衡和静不平衡时的系统响应

为充分研究滚仰式稳定平台的质量不平衡对系统的影响,本文同时考虑存在质量动不平衡和质量静不平衡下系统的响应。静不平衡实验条件和动不平衡实验条件与上文相同,可得在系统中同时加入两种不平衡时,系统外框架和内框架的静不平衡力矩、动不平衡力矩和响应速度,分别如图15～图20所示。

图15 外框质量静不平衡力矩 图16 内框质量静不平衡力矩

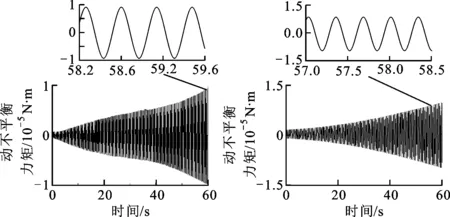
图17 外框质量动不平衡力矩 图18 内框质量动不平衡力矩

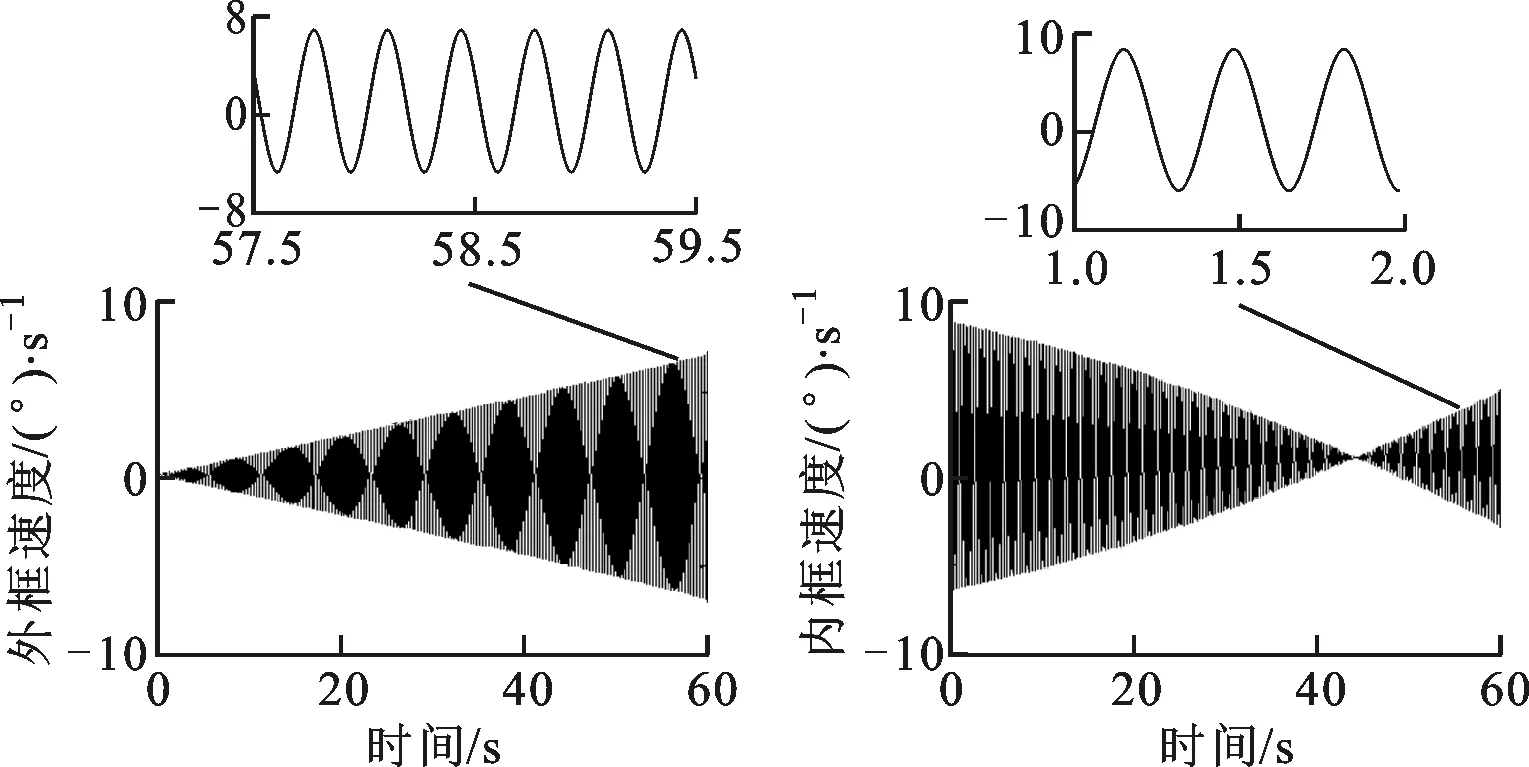
图19 存在质量不平衡时外框阶跃响应 图20 存在质量不平衡时内框阶跃响应

与仅考虑静不平衡时比较分析可知,在加入动不平衡后,考虑导弹的有效行程,可知外框架和内框架的静不平衡力矩分别为0.216 9、0.014 31 N·m,动不平衡力矩分别为9.56、1.216×10-4N·m。与静不平衡力矩相比,系统动不平衡力矩可以忽略,即系统静不平衡是影响系统稳定和响应的主要质量不平衡因素。在减小质量不平衡力矩时,在设计、加工和装配过程中,应采取措施主要减小质量静不平衡力矩。

5 实验研究

研究分析俯仰偏航式稳定平台质量不平衡时,目前的研究手段主要以仿真为主,主要是因为:实验室条件下难以模拟导引头实际工况,例如80g过载的施加、内外框架偏心距和惯性积的准确测量等;针对导引头稳定系统,其系统组成元件如陀螺、角位置测量元件、电机和探测器等因应用领域的特殊性而价格较高,在大过载情况下系统不平衡力矩会非常大,这会造成元器件的损坏。因此,目前对导引头系统的质量不平衡问题的研究方法是通过测量技术手段测量出系统实际质心位置,然后通过机械配平进行质量不平衡的消除。综合上述分析,为了确保导引头稳定平台的安全,结合实验室实验条件,本文提出质量动不平衡补偿实验方法,主要研究基于模型的动不平衡补偿,如图21所示。

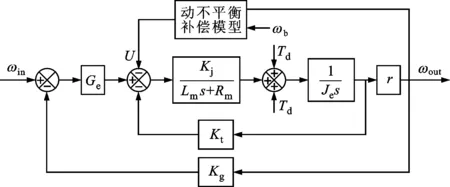
图21 动不平衡补偿原理图

在实际系统存在动不平衡力矩时,采用基于动不平衡模型的前馈补偿方案补偿动不平衡力矩。图21中ωb为弹体典型扰动速度,可以由三轴转台模拟,U为基于动不平衡模型转换得到的电压信号。力矩到电压信号的转换公式为[14]

(24)

动不平衡模型中的惯性积采用上文提到的理论设计值,分别采用1(°)/s的阶跃指令,比较施加动不平衡补偿前后滚仰式稳定平台的系统响应,滚转框和俯仰框补偿对比图分别如图22、图23所示。

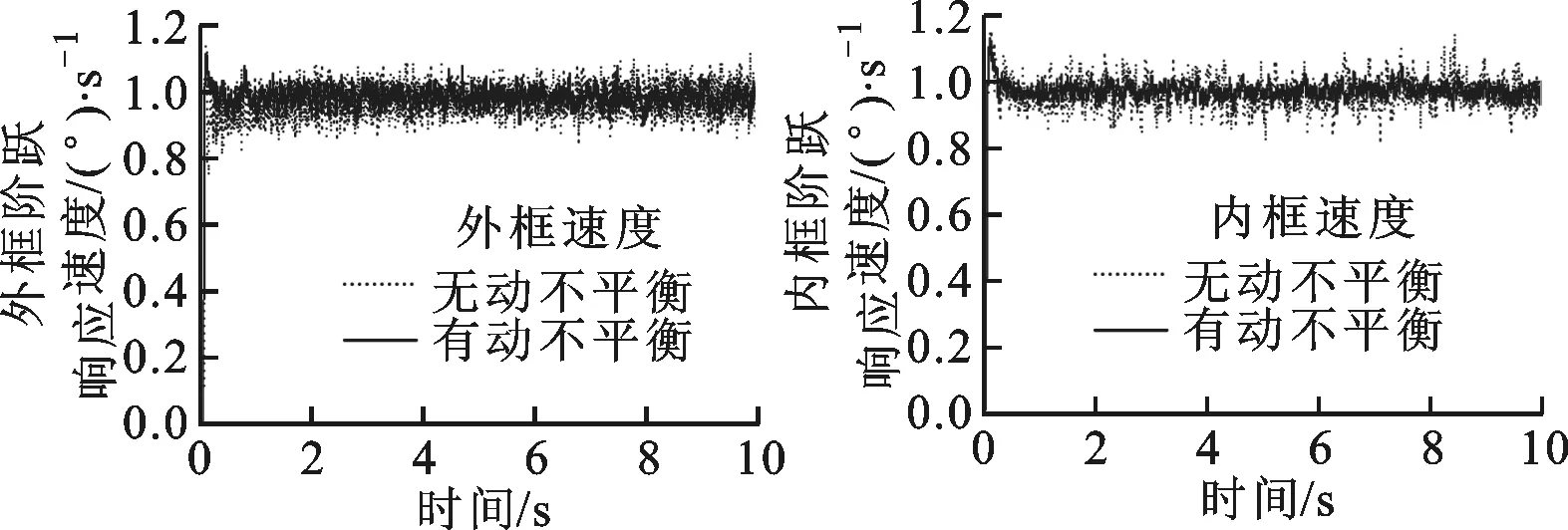
图22 滚转框动不平衡 图23 俯仰框动不平衡 补偿对比图 补偿对比图

根据图22可知,未补偿动不平衡前,滚转框阶跃响应稳态平均值为0.968(°)/s,均方差为0.039 4,补偿动不平衡后,滚转框阶跃响应稳态平均值为0.981(°)/s,均方差为0.025 6,分别提高1.34%和35.03%。根据图23可知,未补偿动不平衡前,俯仰框阶跃响应稳态平均值为0.964(°)/s,均方差为0.042 4,补偿动不平衡后,俯仰框阶跃响应稳态平均值为0.970 2(°)/s,均方差为0.019,分别提高0.64%和55.19%。根据动不平衡补偿前后对比可知,采用动不平衡补偿后,系统响应稳态误差及其波动均得到改善,从而验证了动不平衡模型的有效性。

6 结 论

本文研究了滚仰式稳定平台质量不平衡问题,在建立的质量静不平衡和动不平衡模型基础上,采用实际设计参数,研究了质量不平衡对系统的影响。针对本文的滚仰式稳定平台,研究结果表明:弹体扰动速度是造成质量不平衡力矩和系统稳态响应周期性变化的原因;静不平衡是系统振荡的主要原因;系统动不平衡力矩对系统响应的超调量影响可忽略,主要影响系统稳态误差。本文对滚仰式稳定平台质量不平衡的研究对其设计、加工及装配具有一定指导意义。今后将开展滚仰式稳定平台质量不平衡问题的实验研究,着重研究不平衡力矩的测量及消除方法。

[1] 李贤涛, 张葆, 沈宏海. 基自抗扰控制技术提高航空光电稳定平台的扰动隔离度 [J]. 光学精密工程, 2014, 22(8): 2223-2231. LI Xiantao, ZHANG Bao, SHEN Honghai. Improvement of isolation degree of aerial photoelectrical stabilized platform based on ADRC [J]. Optics and Precision Engineering, 2014, 22(8): 2223-2231.

[2] 赵明, 朱明超, 白杨, 等. 应用LPOE公式与遗传算法标定导引头运动学参数 [J]. 光学精密工程, 2014, 22(3): 687-694. ZHAO Ming, ZHU Mingchao, BAI Yang, et al. Calibration of kinematic parameters of seekers by LPOE formula and genetic algorithm [J]. Optics and Precision Engineering, 2014, 22(3): 687-694.

[3] 林德福, 王志伟, 王江. 滚-仰式导引头奇异性分析与控制 [J]. 北京理工大学学报, 2010, 30(11): 1265-1269. LIN Defu, WANG Zhiwei, WANG Jiang, Singularity analysis of roll-pitch seeker and its control strategy [J]. Transactions of Beijing Institute of Technology, 2010, 30(11): 1265-1269.

[4] 吴海龙, 贾宏光, 魏群, 等. 滚仰式导引头跟踪回路角增量优化 [J]. 光学精密工程, 2014, 22(10): 2787-2795. WU Hailong, JIA Hongguang, WEI Qun, et al. Optimization of angle increments in tracking loop for roll-pitch seeker [J]. Optics and Precision Engineering, 2014, 22(10): 2787-2795.

[5] 肖仁鑫, 张聘义, 胡海双, 等. 滚俯仰式红外导引头稳定平台控制与仿真 [J]. 红外与激光工程, 2007, 36(s1): 363-365. XIAO Renxin, ZHANG Pinyi, HU Haishuang, et al. Control and simulation of roll-pitch infrared seekers stabilization platform [J]. Infrared and Laser Engineering, 2007, 36(s1): 363-365.

[6] 王志伟, 祁载康, 王江. 滚-仰式导引头跟踪原理 [J]. 红外与激光工程, 2008, 37(2): 274-277. WANG Zhiwei, QI Zaikang, WANG Jiang. Tracking principle for roll-pitch seeker [J]. Infrared and Laser Engineering, 2008, 37(2): 274-277.

[7] CHUN Lianglin, YI-HSING Hsiao. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop [J]. IEEE Transactions on Control Systems Technology, 2001, 19(1): 108-121.

[8] 董安华, 王召义, 刘 杰. 某红外成像导弹的静平衡问题分析 [J]. 航空兵器, 2005(5): 62-64. DONG Anhua, WANG Zhaoyi, LIU Jie. Analysis of the static balance for an infrared imaging missile [J]. Aero Weaponry, 2005(5): 62-64.

[9] MCKERLEY C W. A model for a two degree of freedom coupled seeker with mass imbalance [J]. IEEE Proceedings on Control Systems Technology, 1996, 9(1): 84-87.

[10]房建成, 戚自辉, 钟麦英. 航空遥感用三轴惯性稳定平台不平衡力矩前馈补偿方法 [J]. 中国惯性技术学报, 2010, 18(1): 38-43. FANG Jiancheng, QI Zihui, ZHONG Maiying. Feedforward compensation method for three axes inertially stabilized platform imbalance torque [J]. Journal of Chinese Inertial Technology, 2010, 18(1): 38-43.

[11]于爽, 付庄, 赵辉, 等. 惯性平台不平衡力矩测试方法及补偿控制 [J]. 上海交通大学学报, 2008, 42(10): 1692-1696. YU Shuang, FU Zhuang, ZHAO Hui, et al. Measurement method and compensation control for unbalanced moment of inertial platform [J]. Journal of Shanghai Jiaotong University, 2008, 42(10): 1692-1696.

[12]朱华征, 范大鹏, 张文博, 等. 质量不平衡力矩对导引头伺服机构性能影响分析 [J]. 红外与激光工程, 2009, 38(5): 767-772. ZHU Huazheng, FAN Dapeng, ZHANG Wenbo, et al. Influence analysis of the mass imbalance torque on the performance of seeker servo mechanism [J]. Infra-

red and Laser Engineering, 2009, 38(5): 767-772.

[13]MAHER A, AHMAD R V, ALIREZA T, et al. Research on the cross-coupling of a two axes gimbal system with dynamic unbalance [J]. International Journal of Advanced Robotic Systems, 2013(10): 357.

[14]于伟, 马佳光, 李锦英, 等. 基于LuGre模型实现精密伺服转台摩擦参数辨识及补偿 [J]. 光学精密工程, 2011, 19(11): 2736-2743. YU Wei, MA Jiaguang, LI Jinying, et al. Friction parameter identification and friction compensation for precision servo turning table [J]. Optics and Precision Engineering, 2011, 19(11): 2736-2743.

(编辑 赵炜)

Analysis of Mass Imbalance for Roll-Pitch Inertial Stabilized Platform

WU Hailong1,2, JIA Hongguang1, WEI Qun1, JIANG Huhai3, ZHU Ruifei1

(1. Changchun Institute of Optics Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China; 2. University of Chinese Academy of Sciences, Beijing 100039, China; 3. South-West Institute of Technical Physics, Chengdu 610041, China)

Static imbalance and dynamic imbalance of mass for a roll-pitch inertial stabilized platform (RPISP) are analyzed to study the effects of the mass imbalance (MI) on the control system of the RPISP. Reasons and classification of MIs in the RPISP are presented and an MI mathematical model of the RPISP is given by using the theorem of moment of momentum. Then, the MI model is rebuilt in Simulink with actual parameters of the roll-pitch inertial stabilized platform and the effects of the MI on the RPISP are researched through different simulations. A compensation research to the mass dynamic imbalance is implemented through experiments. The simulation results show that the impact of the dynamic mass imbalance (DMI) on the overshoot is negligible and its main effect is on steady errors. The static mass imbalance (SMI) is the primary cause of the oscillation and instability of the system. After the compensation, the average steady-state response values of the roll gimbal and the pitch gimbal are improved by 1.34%and 0.64%, respectively and their mean square deviations are reduced by 35.03%and 55.19%, respectively. The results are useful for the analysis and elimination of the MI existed in RPISPs.

mass imbalance; roll-pitch stabilized platform; imbalance torque

2014-11-19。

吴海龙(1988—),男,博士生;贾宏光(通信作者),男,研究员,博士生导师。

中科院三期创新基金资助项目(YYYJ-1122)。

时间:2015-03-03

10.7652/xjtuxb201505017

TH113.2;TP273;E927

A

0253-987X(2015)05-0108-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150303.1110.006.html