涡旋核心分布对斜置肋片蒸汽冷却通道换热特性的影响

费继友,曾俊雄,高铁瑜,朱江楠,徐勋,肖萍

(1.西安交通大学能源与动力工程学院,710049,西安;2.大连交通大学机械工程学院,116028,辽宁大连;3.中国石油宁夏石化公司,750026,银川)



涡旋核心分布对斜置肋片蒸汽冷却通道换热特性的影响

费继友1,2,曾俊雄2,高铁瑜1,朱江楠1,徐勋1,肖萍3

(1.西安交通大学能源与动力工程学院,710049,西安;2.大连交通大学机械工程学院,116028,辽宁大连;3.中国石油宁夏石化公司,750026,银川)

数值计算了宽高比为2∶1,雷诺数为1×104～6×104,肋角度分别为30°、60°、90°时蒸汽冷却带肋通道,采用流场涡旋核心显示技术分析了各肋角度下带肋通道涡旋的产生、演变过程、形态变化以及分布规律,研究了涡旋分布规律对通道换热系数的影响。结果表明:肋角度对带肋通道涡旋形态和分布规律有较大影响,90°通道主要由横向涡组成,30°、60°通道主要由纵向涡和主涡组成;纵向涡的换热特性比横向涡更好,30°、60°通道平均换热系数比90°通道高;30°通道纵向涡的分支以及流体的黏性耗散会导致纵向涡涡旋强度和尺度减小、纵向涡的换热性能削弱,这使得30°通道平均换热系数比未发生纵向涡分支的60°通道低;相对于边界层的距离、涡旋半径,涡旋强度、涡旋核心是影响涡旋强化换热的更重要的参数。该结果可为主动控制带肋通道涡旋强化换热研究提供参考。

数值模拟;带肋通道;涡旋结构;换热特性

提高燃气透平进口温度是提高燃气轮机热效率的有效方法,当今先进燃气轮机透平的进口温度在1 500～1 700 ℃之间,远超过燃气轮机叶片材料的许用温度(约800 ℃),因此必须发展先进燃机轮机叶片冷却技术,以保护叶片免受高温腐蚀和损伤。燃气轮机常用冷却措施包括气模、冲击、强化对流、绕流柱等。在过去几十年中,以空气作为冷却介质的带肋通道强化对流冷却技术,国内外学者做了详细的研究[1-5]。蒸汽的热物性比空气更好,因此以蒸汽作为冷却介质的带肋通道冷却技术比空冷具有明显的优势[6-7]。史晓军等通过实验的方法建立了蒸汽冷却带肋通道反映雷诺数Re、肋角度和宽高比影响的传热和摩擦特性实验关联式[8]。税琳琪等通过实验和数值模拟的方法研究了肋角度α=90°时矩形通道内蒸汽过热度、压力以及Re对蒸汽换热性能的影响[9]。刘加增等通过实验的方法研究了通道宽高比W∶H分别为1∶4、1∶2、1∶1,α=45°,60°时蒸汽沿矩形通道轴向和径向传热系数的分布规律[10],结果表明45°肋矩形通道沿轴向中心线平均努塞尔数比60°肋矩形通道高15%～25%,沿着通道径向换热系数逐渐降低,这可能是斜置肋片沿肋展方向产生二次旋流引起的。Han等做了同样类似的实验[11],研究表明90°肋矩形通道内空气换热系数沿通道径向分布比较均匀,而斜置肋片通道内空气换热系数沿径向分布逐渐降低,这可能是斜置肋片产生二次流动引起的。朱江楠等采用涡旋核心分析方法研究了W∶H=1∶1、α=45°带肋通道涡旋分布及其对努赛尔数Nu的影响,结果表明,高强度涡旋区域比没有涡旋的区域的努赛尔数至少高一倍以上[12]。史晓军等通过实验研究了W∶H=2∶1、α=30°,45°,60°,90°时蒸汽与空气的换热性能,研究表明,蒸汽平均换热系数是空气的1.19～1.32倍,60°肋具有最优的换热性能[13]。

综上所述,不同肋角度带肋通道涡旋(也称二次流)的分布及其对换热系数的影响鲜为人知,因此本文采用流场涡旋核心可视化分析方法研究了不同肋角度带肋通道涡旋的产生、演变过程、分布规律以及对换热系数的影响,研究结果可对进一步优化燃气轮机带肋通道冷却结构、提高冷却效率提供参考。

1 计算方法及数据处理

1.1 物理模型

本文采用的物理模型均与文献[13]中实验研究物理模型相同,以研究W∶H=2∶1、α=30°,60°,90°带肋通道内涡旋分布规律及其对换热性能的影响。计算模型参数如表1所示,表中e为肋高,D为通道水力直径,p为肋间距,L为通道计算长度。计算几何模型如图1所示。

表1 计算模型参数

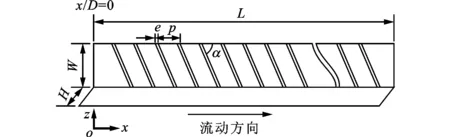
图1 计算通道几何模型

3种不同肋角度带肋通道计算区域均采用结构化网格,带肋壁面和两侧光滑壁面处网格均进行加密处理,以确保所有近壁面第一层网格满足y+<1。

经过网格无关性验证后,α=30°,60°,90°带肋通道的网格数分别为780万、830万和820万,其中60°肋带肋通道网格的局部细节如图2所示。

图2 60°肋带肋通道网格局部细节

1.2 计算方法及边界条件

采用商用软件ANSYS CFX14.5中SSTk-ω湍

流模型求解三维定场不可压缩黏性流体雷诺时均N-S方程,方程中的扩散项和源项离散采用二阶中心差分格式,对流项采用高精度离散格式,各项残差收敛到10-5。为了验证数值计算结果的可靠性,本文工况与文献[13]实验工况相同:3种不同肋角度带肋通道内流动工质为蒸汽,蒸汽进口温度为174 ℃,进口压力为0.3 MPa,Re=1×104～6×104,热流密度q=5 kW/m2。

1.3 计算结果数据处理

流场涡旋核心显示采用CFD-POST中涡旋核心区(vortex core region)功能。局部流场涡旋核心检测方法分为流线、迹线、Q判据、Δ判据、λ2判据、涡旋强度等,其中λ2判据被认为是最有效、最可靠的流场涡旋核心检测方法[14-15]。文献[14]的研究表明:实对称二阶张量S2+Ω2的3个实特征值中,若存在2个负特征值的流场区域,则定义其为涡旋核心区域,即实对称二阶张量S2+Ω2的3个实特征值λ1>λ2>λ3,当λ2<0时,存在涡核,其中u=S+Ω,S为应变率张量,Ω为旋转率张量。特别地,当λ2=0时,流场λ2等值面所围成的涡核区域为全场涡旋核心区,λ2值越小,涡旋核心强度越强。因此,本文采用λ2判据作为计算域内涡旋核心的检测方法。

为了便于处理计算结果,定义相关参数如下。

Re=ρuD/μ,其中μ为蒸汽的动力黏性系数,D=2WH/(W+H)。

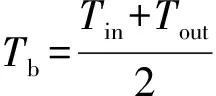
由Dittus-Boelter公式可知,光滑通道充分发展段的Nuo=0.023Re0.8Pr0.4。

由Filonenko经验关联式[16],定义光滑通道内充分发展阶段的fo=(1.58lnRe-3.28)-2。

2 数值计算结果可靠性验证

(a)α=30°

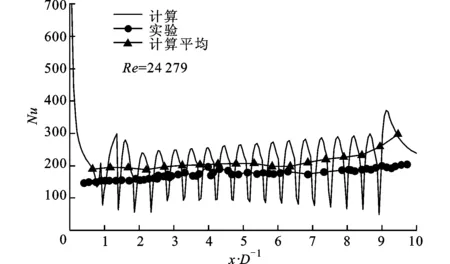
(b)α=60°

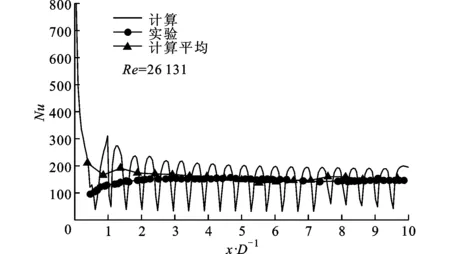
(c)α=90° 图3 3种不同肋角度带肋通道中心线上Nu计算结果与实验对比

图3为α=30°、Re=20 818,α=60°、Re=24 279,α=90°、Re=26 131带肋通道中心线上Nu的计算结果与文献[13]实验结果对比。从图中可以看出,数值计算平均值与实验值吻合良好,但是在带肋通道进口和出口处Nu与实验值误差偏大。这可能是气流受到不同进口效应扰动以及出口处数值计算通道几何形状的变化所致。α=30°,60°,90°带肋通道中心线上Nu的数值计算平均值比文献[13]实验结果分别高出8.1%、17.14%、9.02%,α=60°带肋通道数值计算与实验结果误差相对较大。这里可能存在两方面的原因:一是实验本身存在8%的不确定度误差;二是实验研究带肋通道带肋面厚度为3 mm,存在三维导热问题,实验热电偶测得的温度实际上是经过导热均匀化后的温度,而数值计算并没有考虑带肋壁面导热问题,这就导致了计算结果偏高。但是,本文数值计算误差是可以接受的。

3 计算结果与分析

3.1 涡旋分布规律分析

本文数值计算了α=30°,60°,90°带肋通道,Re=1×104～6×104时的工况,并研究了Re=6×104时不同肋角度带肋通道流场涡旋的产生、演变、形态及分布规律。

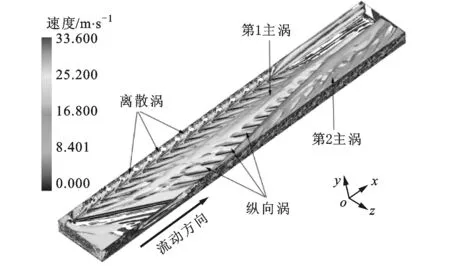
(a)α=30°

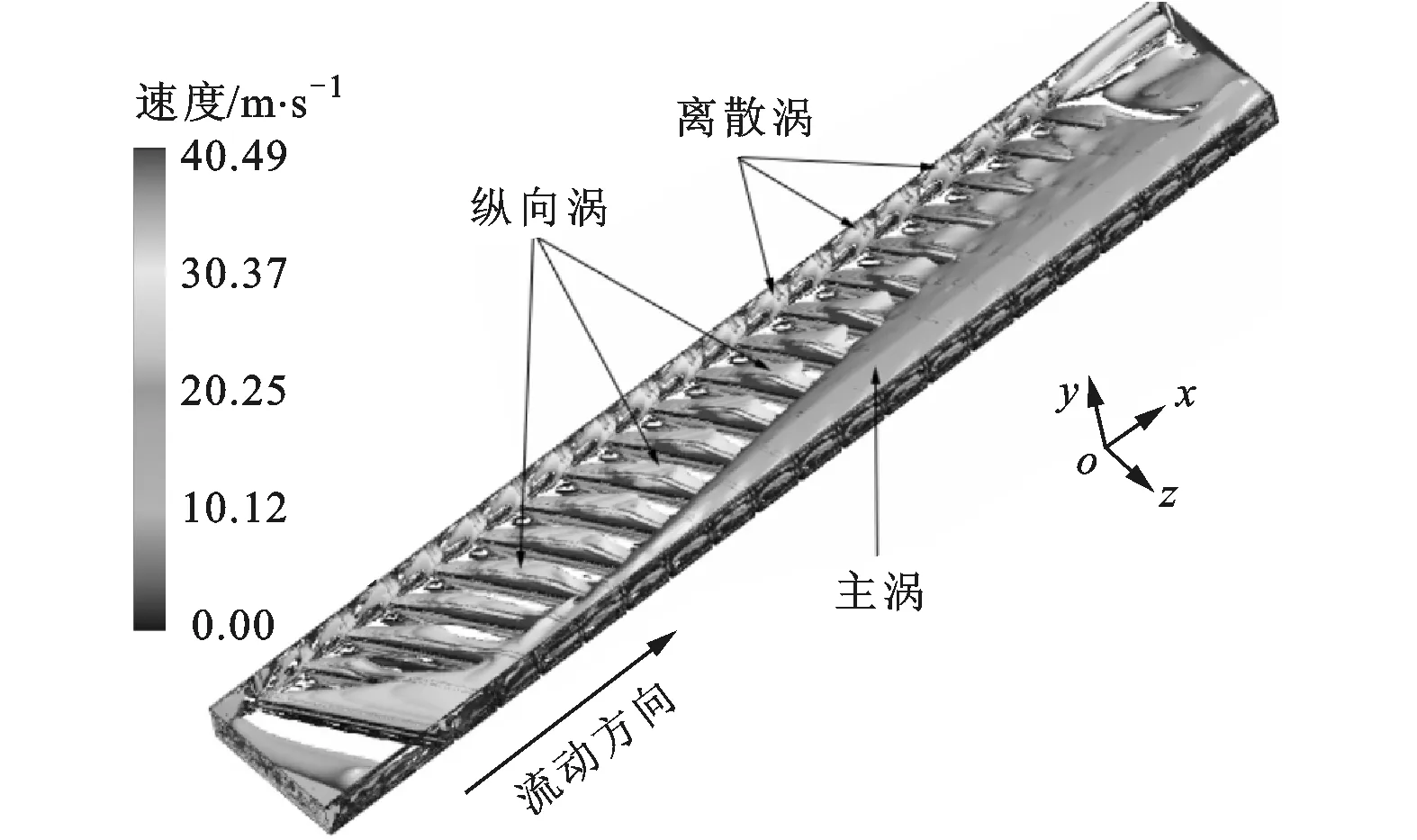
(b)α=60°

(c)α=90°图4 3种不同肋角度带肋通道全场涡旋分布

图4为α=30°,60°,90°带肋通道全场涡旋分布图。从总体上看,不同α带肋通道涡旋分布规律差别较大,但α=30°和α=60°带肋通道涡旋分布存在一定的相似性,主要由左侧光滑壁面上的离散涡、带肋面上纵向涡、主流通道主涡组成。它们之间所不同的是:α=30°带肋通道充分发展段存在第1主涡和第2主涡,主涡均由纵向涡发展而来,主涡的旋转中心轴线与主流方向平行;纵向涡分布在肋顶上,且沿着肋展方向发展,其旋转中心轴线与肋展方向平行。图4c中α=90°带肋通道涡旋分布规律与α=30°,60°完全不同,其充分发展段涡旋分布具有明显的周期性,主要由分布在肋顶上的横向涡组成。横向涡与纵向涡的区别在于其旋转中心轴线与主流方向垂直。由于3种不同带肋通道的进口段斜置肋片的角度不同,所以进口段的涡旋形态有所不同。

为了进一步分析和阐明带肋通道涡旋的产生、演变机理,本文将分别阐述了3种不同带肋通道的进口段和充分发展段涡旋的异同。

图5为α=30°,60°,90°带肋通道进口涡旋分布图。从图中可以看出,3种不同带肋通道进口处均存在一个扰动涡,扰动涡是进口处气流受到通道第1根斜置肋片的扰动产生的,其发展方向分别与斜置肋片展向方向相同,最后随主流一起流入下游而耗散掉。从图5a、图5b可以看出,α=30°,60°带肋通道进口处涡系均由纵向涡和主涡组成,这些纵向涡是气流在每一根肋片前缘出现流动分离而产生的,并沿着肋展方向发展且最后汇入主涡,这就使得主涡沿着主流发展的过程中的尺度越来越大,在出口处的体积能为通道宽度处的1/2左右,见图4a、图4b。进口处的纵向涡与充分发展段纵向涡有所不同的是,进口处纵向涡受主流的影响较大,几乎能横跨2、3根肋片。α=30°,60°带肋通道进口处纵向涡的区别是:α=30°带肋通道进口纵向涡在沿着肋展方向发展的过程中出现了分支纵向涡,这些分支纵向涡一部分横跨2根肋片并汇入位于主流中心区域的第1主涡,另一部分沿着肋展方向发展,最后汇入第2主涡,见图5a;α=60°带肋通道进口处纵向涡并没有出现分支现象,纵向涡沿着肋展方向发展,最后汇入位于通道右侧光滑壁面的主涡,并随着主涡一起运动到通道下游。从图5c可以看出,α=90°带肋通道进口处第1个横向涡同样因受到主流的影响而横跨了2根肋片,以至于在第2根肋片前缘处气流流动分离受阻,由此阻碍了第2个横向涡的形成,而从第3根肋片开始,横向涡在通道内出现周期性变化。

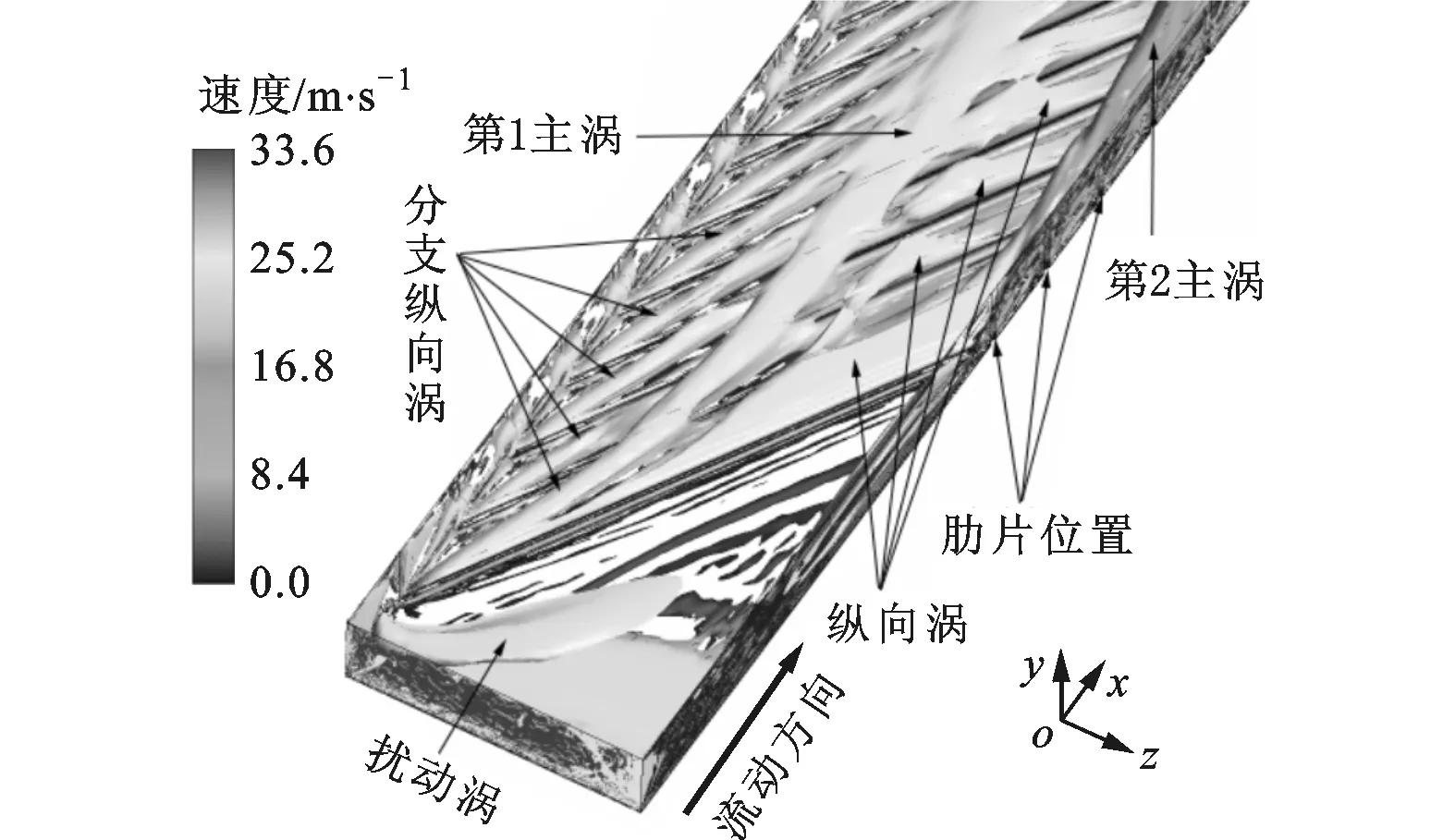
(a)α=30°

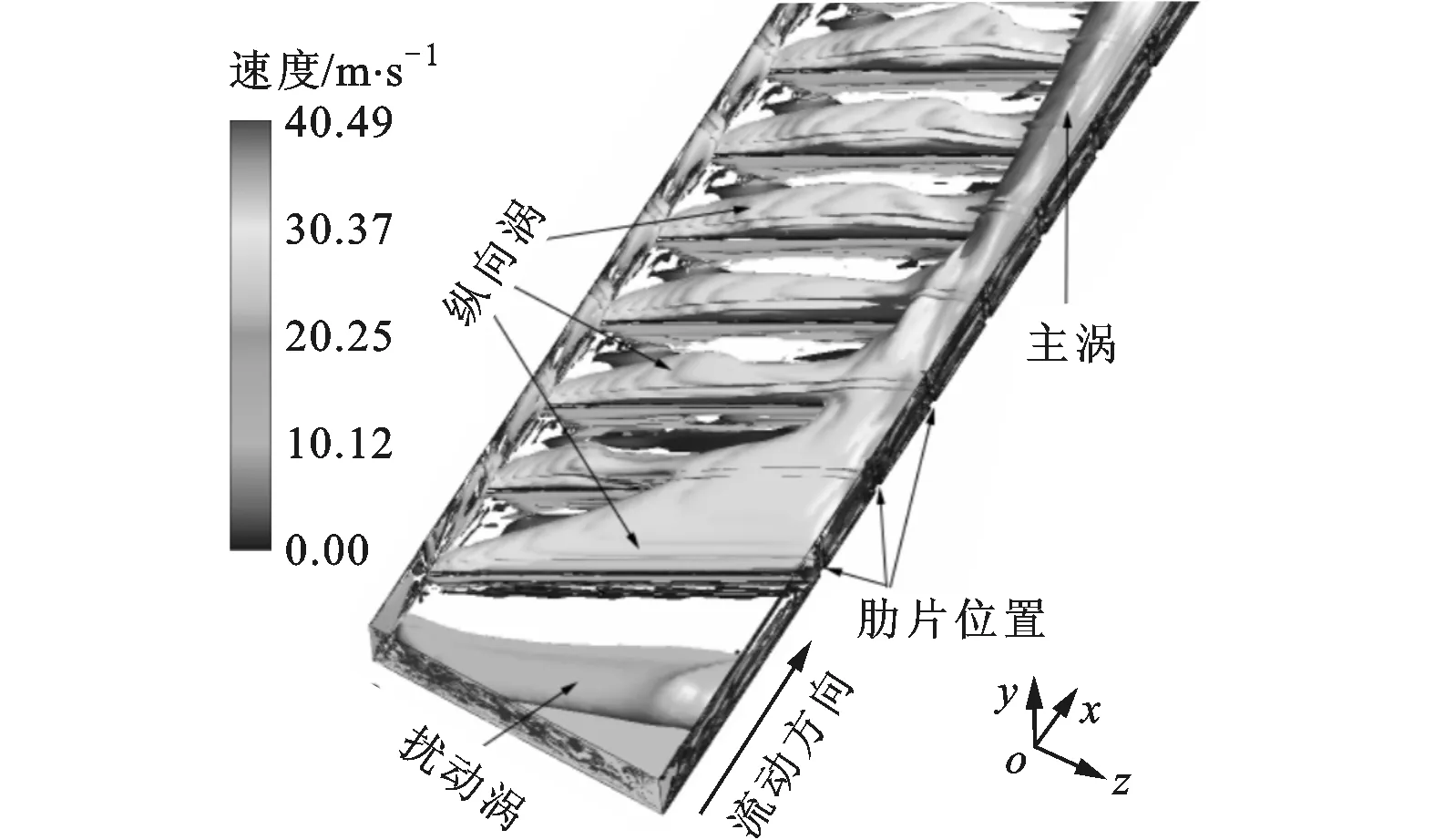
(b)α=60°

图6为不同α带肋通道充分发展段涡旋分布。α=90°带肋通道充分发展段横向涡旋分布呈周期性变化,涡旋结构相对单一,这里不再赘述。为了进一步分析α=30°,60°带肋通道充分发展段涡旋分布特征,将图6a所有涡旋细化为图6b所示的涡旋分布,此时λ2=-157 364。从图6b、图6c可以看出,α=30°,60°带肋通道充分发展段涡系主要由纵向涡、角涡、诱导涡、主涡、离散涡组成。纵向涡是气流在肋片前缘处出现流动分离而产生的,在α=30°带肋通道沿着肋展方向的下游区域,一部分分支纵向涡与角涡汇合,最后一起汇入主涡,另外一部分在肋顶上发展至主涡。角涡在每一根肋片前缘肋根处的高压区(局部滞止区)形成,并沿着前缘肋根方向发展,直至汇入右侧光滑壁面处的主涡中。诱导涡在每一根肋片后缘肋根处的低压区形成(见图6b),最后也汇入主涡,而在图6c中诱导涡被纵向涡覆盖。离散涡在主流左侧光滑壁面与每一根肋片的结合处的正上方形成,这可能是气流在此区域受到扰动产生的,它处于离散状态,最后在主流中耗散掉。

(a)α=30°(λ2=0)

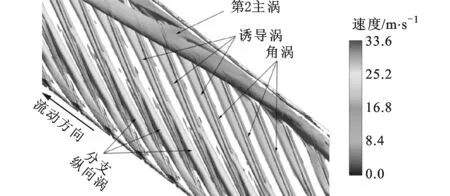
(b)α=30°(λ2=-157 364)

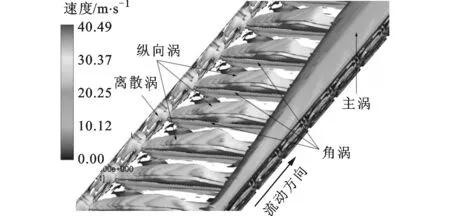
(c)α=60°(λ2=0)图6 不同肋角度带肋通道充分发展段涡旋分布

3.2 涡旋分布对带肋壁面Nu的影响

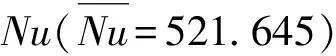
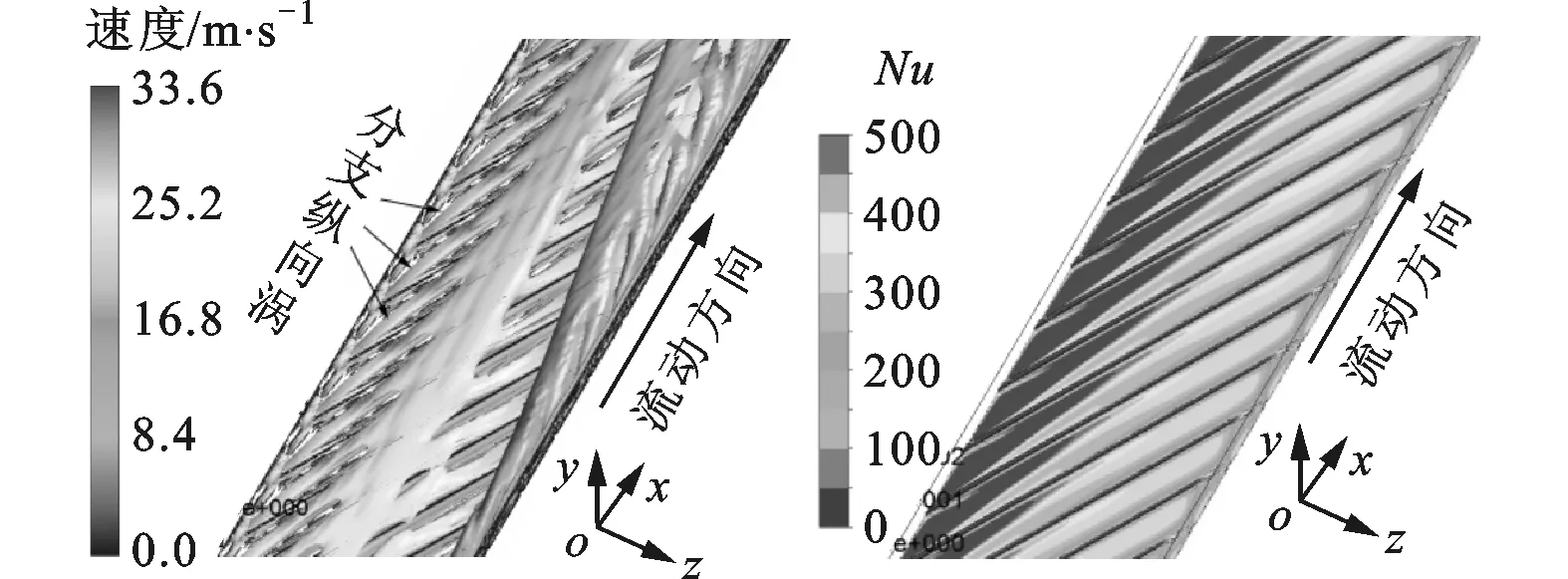
(a)α=30°

(b)α=60°

(c)α=90°图7 不同肋角带肋通道充分发展段涡旋与Nu分布

Gentry等研究了平板上由三角翼涡旋发生器产生的纵向涡与热边界层的相互作用关系,结果表明,相对于热边界层的位置δ*,纵向涡涡旋强度和涡旋核心是影响涡旋强化换热的重要参数,涡旋强度越大,涡旋核心离热边界层越近,涡旋换热效果越好[17]。按照文献[17]定义,涡旋强度环量Γ=2πrVθ,δ*=δc/δb,δc为涡旋核心到壁面的距离,δb为热边界层厚度。

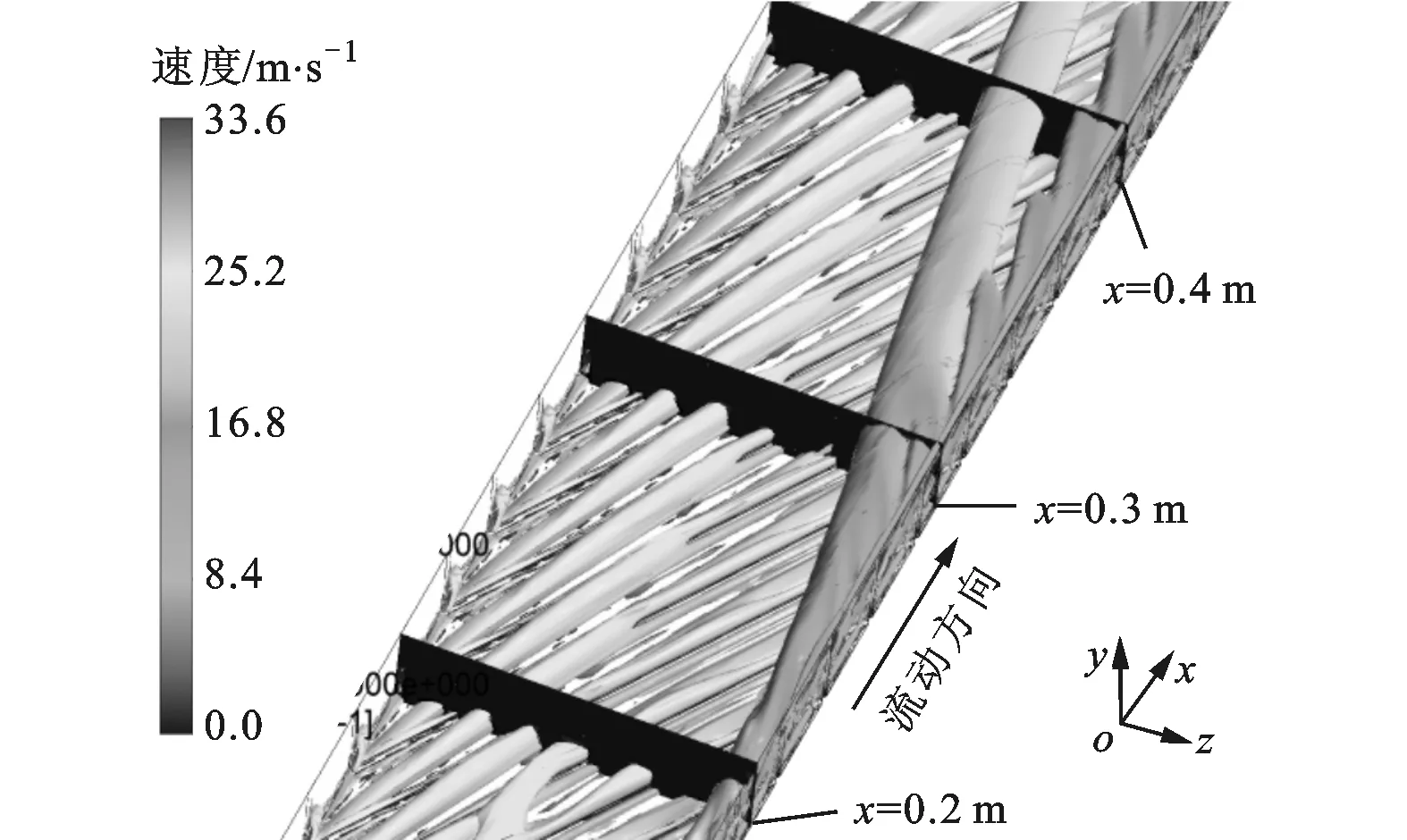
图8 α=30°带肋通道充分发展段x=0.2 m,0.3 m,0.4 m处横截面位置示意

图9 α=30°带肋通道不同横截面纵向涡旋强度分布

图8、图9分别为α=30°带肋通道充分发展段在x=0.2 m,0.3 m,0.4 m处横截面位置与对应横截面上涡旋强度的分布规律。图9a中:数字1～5表示图8中x=0.2 m横截面上纵向涡沿着通道径向变化的编号,括号里的数值分别代表纵向涡涡旋强度;数字6～9代表x=0.2 m横截面上诱导涡;数字10、11代表x=0.2 m横截面上角涡。图9b、图9c所在横截面上涡旋分布规律与图9a相同,纵向涡涡旋强度如图中的数值所示。从图9可以看出,各横截面上2号纵向涡由1号纵向涡发展而来,3号纵向涡由2号纵向涡发展而来,以此类推。沿着通道径向方向,纵向涡涡旋强度逐渐减弱,各横截面上最左端1号纵向涡涡旋强度是5号纵向涡涡旋强度的3.0～4.6倍,但是在图9b、图9c第4和第5根肋片顶端纵向涡涡旋强度有所增大,这可能是该区域纵向涡受到了沿着主流方向发展越来越大的主涡的影响。总体看来,α=30°带肋通内随着分支纵向涡向下游的发展,涡旋强度会逐渐衰减,一方面是由气流的黏性耗散导致,另一方面α=30°带肋通纵向涡分支太多,而且沿肋展方向上游区域的分支纵向涡有一部分汇入第1主涡中,这都会导致纵向涡涡旋强度沿涡旋发展方向逐渐减弱。另外,随着分支纵向涡向下游的发展,热边界层逐渐增厚,温度梯度逐渐减小。综合以上因素,最终导致图7a中α=30°带肋通道Nu沿着径向逐渐减小,换热效果逐渐变差。从通道纵向上看,除了图9c中1号纵向涡涡旋强度明显大于图9a、图9b外,各横截面上的纵向涡涡旋强度和涡旋尺度差异不大,但是沿着主流方向,处在通道最右端的主涡涡旋强度和尺度变化较大,该尺度沿主流方向逐渐增大,这是由纵向涡汇入主涡造成的。尽管主涡有足够大的涡旋强度和尺度,但是它处在主流通道中心区域,距离带肋壁面热边界层较远,即δ*较大,这一方面会削弱主涡对近壁面附近热边界层的扰动或者破坏作用,另一方面大尺度主涡同时也极大地增加了通道内的流动阻力,而流动阻力的增加远大于换热的增强。因此,综合看来,通道内主涡对带肋壁面强化换热贡献不大。相反,位于近壁面附近的纵向涡具有良好的强化换热能力。事实上,对于湍流强化换热而言,由于湍流流动的剧烈掺混作用,使得通道中大分部(除层流底层外)区域已经混合得很充分,这样再增加该区域的扰动只会进一步增加流动阻力,对强化换热作用不大,即只有在层流底层附近产生纵向涡才能实现同功耗下进一步增强强化传热效果,从而达到节能的目的。

图10、图11分别为α=60°带肋通道充分发展段在x=0.2 m,0.3 m,0.4 m处横截面位置与对应横截面上涡旋强度的分布规律。各横截面上由离散涡、纵向涡、主涡组成,纵向涡和主涡强度如图11中的数值所示。从纵向看,纵向涡涡旋强度和尺度差异不大,但主涡尺度沿主流方向逐渐增大。从图10可以看出,α=60°带肋通道纵向涡并没有出现分支,使得纵向涡涡旋强度因分支而产生的损失减小。从图11可以看出,纵向涡在近壁面处的尺度较大,且呈扁平状覆盖在肋片后缘的下游区域,这比α=30°带肋通道纵向涡对下游的影响区域要大得多。综合以上两点得出,α=60°带肋通道换热效果比α=30°更好,但是α=60°带肋通道在靠近右侧带肋壁面的Nu相对较低(见图7d),这是气流的黏性耗散造成涡旋强度衰减和主涡仍然距带肋壁面较远导致。

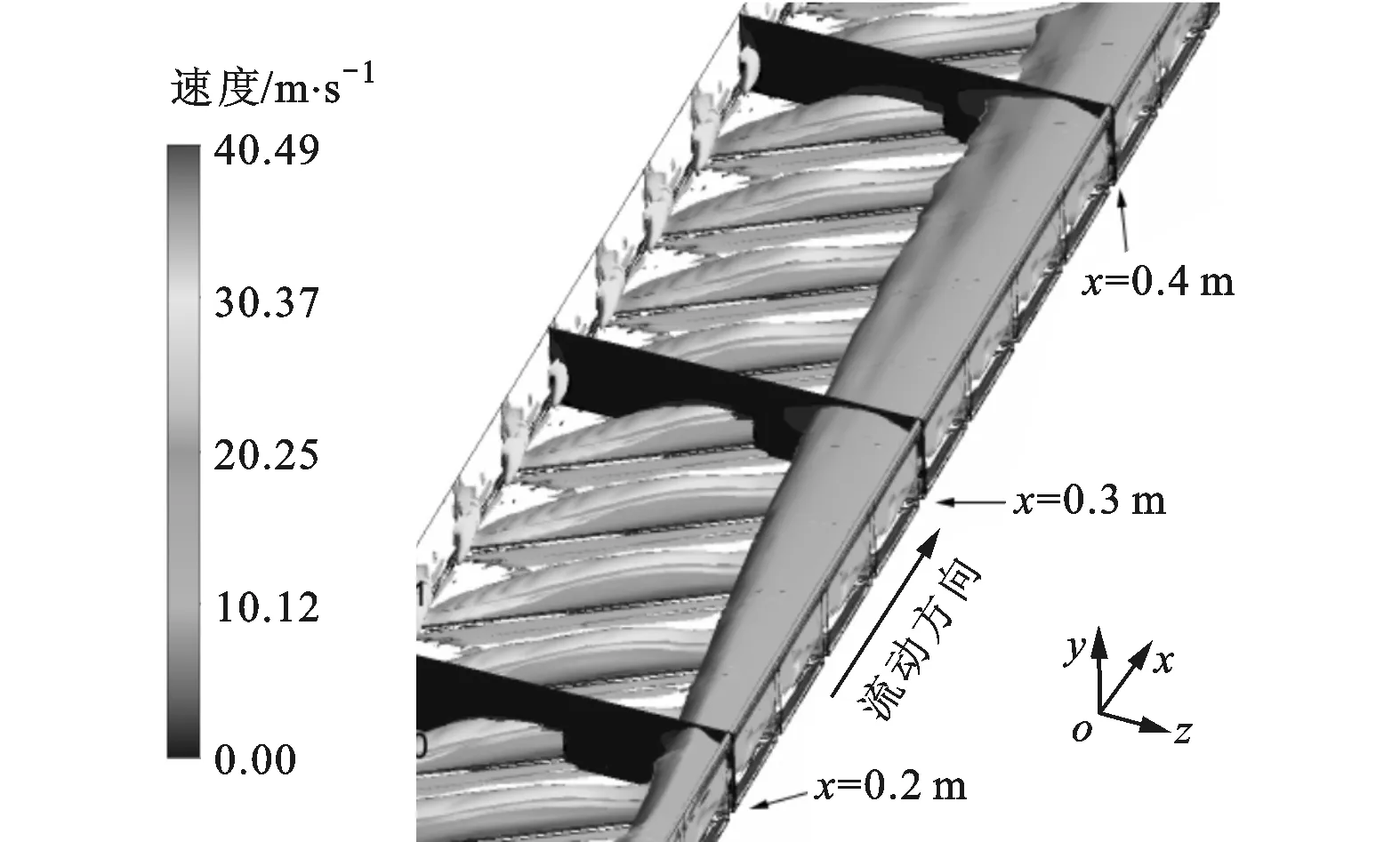
图10 α=60°带肋通道充分发展段x=0.2 m,0.3 m,0.4 m处横截面位置示意

图11 α=60°带肋通道不同横截面纵向涡旋强度分布

由图7c可知,α=90°带肋通道的Nu沿径向分布比较均匀,横向涡尺度和形态沿径向相同,因此可以推测出横向涡涡旋强度沿径向分布相同。事实上,对于横向涡和纵向涡,它们的换热机理截然不同[18]。横向涡强化换热是由流场的不稳定性以及气流的自激振动产生的。横向涡的一侧向下扫,将主流较高动量气流和较低温度气流同时带入边界层,与在边界层内的气流进行强烈的动量和能量的交换,以增大边界层内的温度梯度,减小边界层内速度矢量与温度梯度的夹角,从而增强换热;横向涡的另一侧向上卷起,将边界层内较低动量气流和较高温度气流带入主流,与主流气流再次进行强烈的动量和能量交换。

与横向涡相比,纵向涡除了以上换热机理以外,还具有以螺旋运动的方式向主流下游输运冷热流体的附加对流换热机制,这对下游热壁面边界层具有持续的破坏作用,因此在整个带肋通道内纵向涡比横向涡具有更好的换热效果。

3.3 不同肋角度带肋通道换热性能比较

图12为α=30°,60°,90°带肋通道努塞尔数比随Re的变化。从图中可以看出,α=60°带肋通道努塞尔数比最高,α=30°其次,α=90°最低,α=60°带肋通道平均Nu比分别比α=30°、90°提高了18%和63%。由上文分析可知,这是因为α=60°带肋通道纵向涡结构比α=30°通道分支纵向涡结构和α=90°通道横向涡结构具有更好的换热效果。不同肋角度带肋通道平均Nu数值计算结果与其通道内涡旋强化换热特性相一致。从图12还可以看出,努塞尔数比具有随Re的增加而逐渐降低的趋势,努塞尔数比降幅在3.9%～14.2%之间。

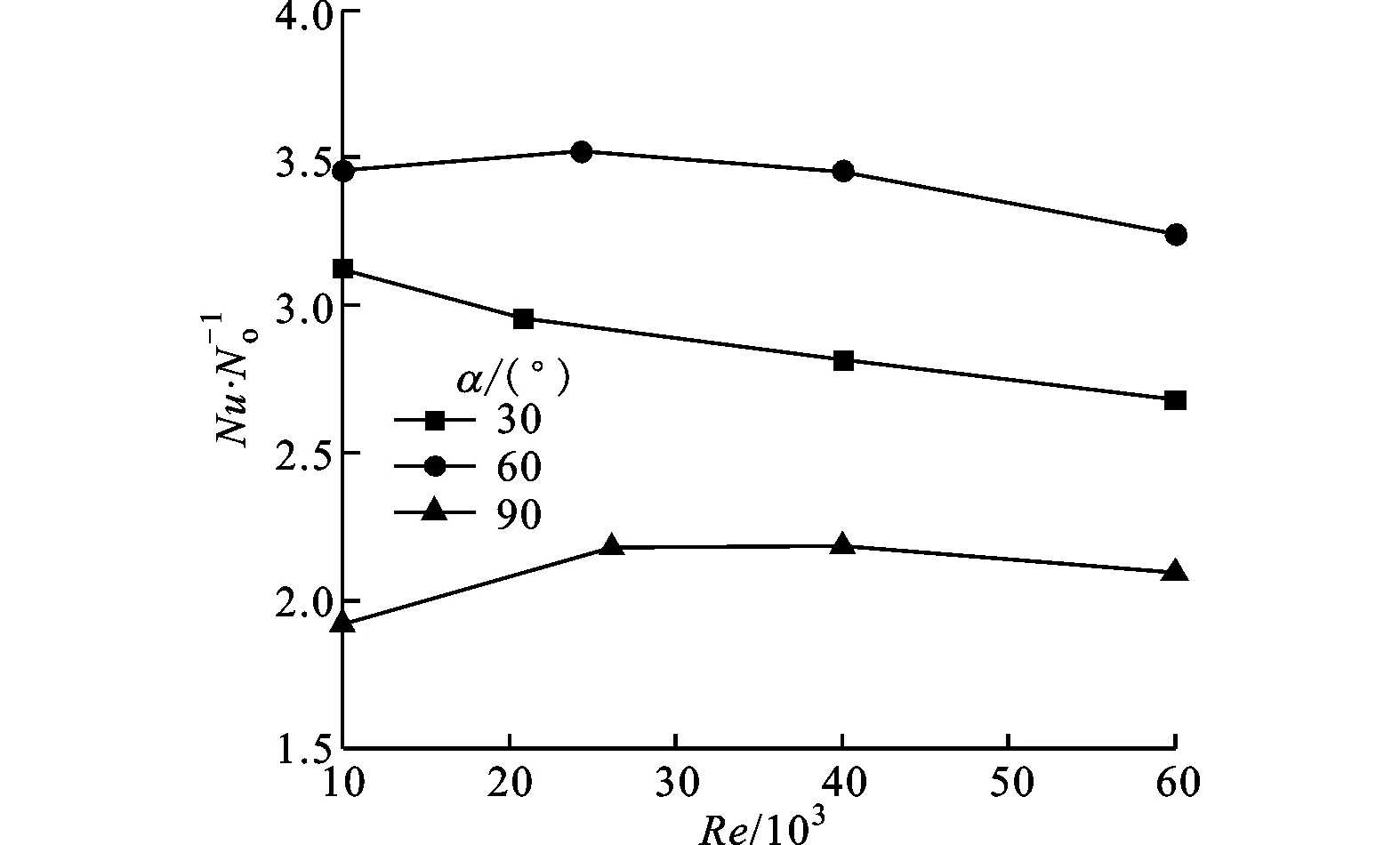
图12 不同肋角度通道努赛尔数比随雷诺数的变化

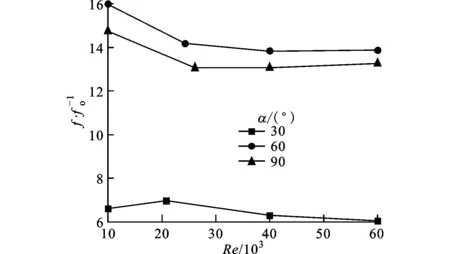
图13 不同肋角度通道摩擦系数比随雷诺数的变化

图13为α=30°,60°,90°带肋通道摩擦系数比随Re的变化。从图中可以看出,α=60°,90°通道摩擦系数比大约是α=30°通道的2.2～2.4倍,这说明α=30°带肋通道压损很小。α=60°,90°通道摩擦系数比相差不大,约5.7%～8.8%,这表明维持α=60°,90°通道纵向涡和横向涡结构的运动,需要比α=30°带肋通道消耗更多的能量。

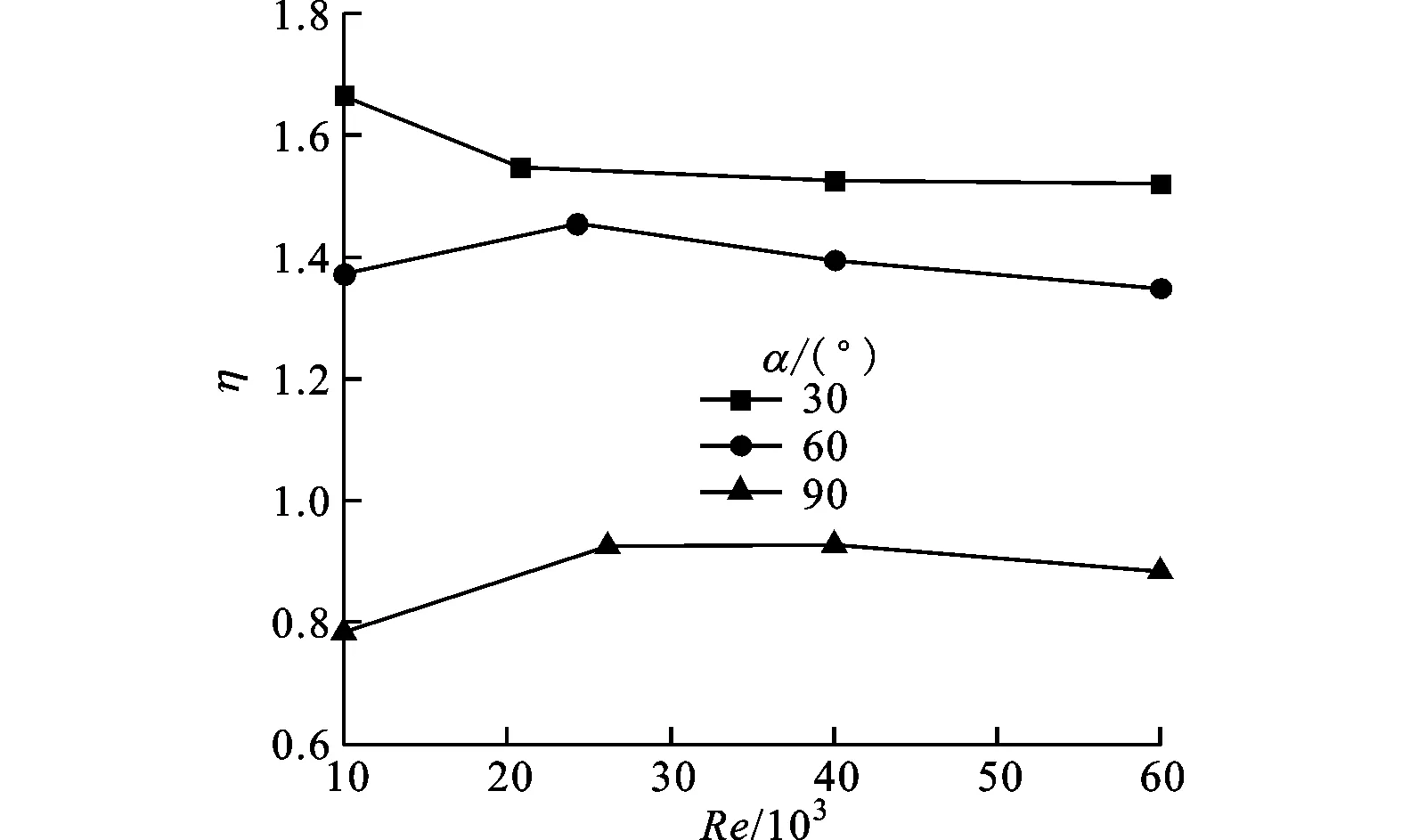
图14 不同肋角度通道换热因子随雷诺数的变化

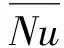
4 结 论

本文通过数值模拟方法、采用流场涡旋核心显示技术,详细地阐述了α=30°,60°,90°带肋通道内不同类型涡旋的产生、演变过程、形态变化以及分布规律,分析了带肋通道不同类型涡旋结构对换热系数的影响,并得出以下结论。

(1)不同角度的斜置肋片对带肋通道内涡旋形态以及分布规律具有重要影响,其中:α=90°带肋通道主要以横向涡旋结构为主,沿着主流方向呈周期性分布;α=30°,60°带肋通道主要以纵向涡和主涡结构为主,纵向涡沿着肋展方向发展,最后汇入主涡且以螺旋运动的方式流向下游。

(2)纵向涡比横向涡具有更好的换热特性,因此α=30°,60°带肋通道Nu比α=90°的高。α=30°通道出现纵向涡分支,这使得近壁面的纵向涡涡旋强度和涡旋尺度在沿着涡旋螺旋前进方向逐渐减小,由此削弱了对边界层的扰动能力,同时也减小了对边界层的影响区域。所以,α=30°通道Nu要比未发生纵向涡分支的α=60°低。

(3)α=30°、60°带肋通道在靠近右侧光滑壁面的主涡位于通道主流区域,距离边界层较远,对强化换热贡献不大,这也会导致靠近右侧光滑壁面的带肋面Nu较低。

(4)相对于边界层的位置δ*、涡旋核心半径r,涡旋强度、涡旋核心是影响涡旋强化换热的更重要的参数,该结果可为主动控制涡旋强化换热研究提供参考。

[1] PARK J S, HAN J C, HUANG Y, et al. Heat transfer performance comparisons of five different rectangular channels with parallel angled ribs [J]. International Journal of Heat and Mass Transfer, 1992, 35(11): 2891-2903.

[2] HAN J C, PARK J S. Heat transfer and friction characteristics in rectangular channels with rib turbulators [J]. Journal of Heat Transfer, 1988, 110(2): 321-328.

[3] HAN J C, OU S, PARK J S, et al. Augmented heat transfer in rectangular channels of narrow aspect ratios with rib turbulators [J]. International Journal of Heat and Mass Transfer, 1989, 32(9): 1619-1630.

[4] 杨力, 阚瑞, 任静, 等. 带气膜孔内部冷却通道的流动与传热特性 [J]. 工程热物理学报, 2011, 32(8): 1385-1388. YANG Li, KAN Rui, REN Jing, et al. Aero-and thermodynamic features of the flow fields in the internal cooling channels with film cooling holes [J]. Journal of Engineering Thermophysics, 2011, 32(8): 1385-1388.

[5] 阚瑞, 陈伟, 任静, 等. 梯形带肋内部冷却通道流动及传热特性 [J]. 工程热物理学报, 2010, 31(5): 753-756. KAN Rui, CHEN Wei, REN Jing, et al. Aero-thermo dynamical characteristics in a ribbed trapezoidal internal cooling system [J]. Journal of Engineering Thermophysics, 2010, 31(5): 753-756.

[6] LIU Jiazeng, GAO Jianming, GAO Tieyu. An experimental investigation of heat transfer characteristics in steam-cooled square channel with rib turbulators, 2011-GT2011-46134 [R]. New York, USA: ASME, 2011.

[7] SHUI Linqi, GAO Jianming, XU Liang, et al. Numerical investigation of heat transfer and flow characteristics in a steam-cooled square ribbed duct, 2010-GT2010-22407 [R]. New York, USA: ASME, 2010.

[8] 史晓军, 税琳棋, 高建民, 等. 蒸汽冷却带肋矩形通道传热和压降实验关联式 [J]. 西安交通大学学报, 2013, 47(11): 1-6. SHI Xiaojun, SHUI Liqi, GAO Jianming, et al. Heat transfer and pressure drop correlations for rectangular channels with ribs [J]. Journal of Xi’an Jiaotong University, 2013, 47(11): 1-6.

[9] SHUI Linqi, GAO Jianming, SHI Xiaojun, et al. The effect of cooling conditions on convective heat transfer and flow in a steam-cooled ribbed duct [J]. Journal of Mechanical Science and Technology, 2014, 28(1): 331-341.

[10]LIU Jiazeng, GAO Jianming, GAO Tieyu, et al. Heat transfer characteristics in steam-cooled rectangular channels with two opposite rib-roughened walls [J]. Applied Thermal Engineering, 2013, 50(1): 104-111.

[11]HAN J C, PARK J S. Developing heat transfer in rectangular channels with rib turbulators [J]. International Journal of Heat and Mass Transfer, 1988, 31(1): 183-195.

[12]ZHU Jiangnan, GAO Tieyu, LI Jun, et al. The effect of vortex core distribution on heat transfer in steam cooling of gas turbine blade internal ribbed channels, 2014-GT2014-25324 [R]. New York, USA: ASME, 2014.

[13]SHI Xiaojun, GAO Jianming, XU Liang, et al. Heat transfer performance comparison of steam and air in gas turbine cooling channels with different rib angles [J]. Heat Mass Transfer, 2013, 49(11): 1577-1586.

[14]JEONG J, HUSSAIN F. On the identification of a vortex [J]. Journal of Fluid Mechanics, 1995, 285(1): 69-94.

[15]SCHAFHITZEL T, VOLLRATH J E, WEISKOPF D, et al. Topology-preservingλ2-based vortex core line detection for flow visualization [C]∥IEEE-VGTC Symposium on Visualization. Piscataway, NJ, USA: IEEE, 2008: 1023-1030.

[16]KLINE S J, MCCLINTOCK F. Describing uncertainties in single-sample experiments [J]. Mechanical Engineering, 1953 (75): 3-8.

[17]GENTRY M C, JACOBI A M. Heat transfer enhancement by delta-wing vortex generators on a flat plate vortex interactions with the boundary layer [J]. Experimental Thermal and Fluid Science, 1997, 14(3): 231-242.

[18]FIEBIG M. Vortices, generators and heat transfer [J]. Transactions of IChemE: Part A, 1998, 76(2): 108-123.

(编辑 苗凌)

Effect of Vortex Core Distribution on Heat Transfer Performance in Steam-Cooled Channels with Inclined Ribs

FEI Jiyou1,2, ZENG Junxiong2, GAO Tieyu1, ZHU Jiangnan1, XU Xun1, XIAO Ping3

(1. School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. School of Mechanical Engineering, Dalian Jiaotong University, Dalian, Liaoning 116028, China; 3. Petro China Ningxia Petrochemical Company, Yinchuan 750026, China)

The steam-cooled channels with rib angles of 30°, 60° and 90°, ducts aspect ratio 2∶1 and Reynolds number ranging from 1×104to 6×104are numerically simulated. The vortex generation, evolution, morphological changes and its distribution are numerically analyzed with flow field vortex core technology and the effect of vortex distribution of ribbed channels on heat transfer performance are also investigated. The result indicates that morphology and distribution of vortex in ribbed channels strongly depend upon the rib angles. In 90° channels transverse vortex dominates, and in 30° and 60° channels longitudinal vortex and main vortex do; the average heat transfer coefficient in 30° and 60° channels is higher than that in 90° channel because of better heat transfer performance of longitudinal vortex than that of transverse vortex; the average heat transfer coefficient in 30° channel is lower than in 60° channel without bifurcated longitudinal vortex because the bifurcated longitudinal vortex in 30° channel and viscous dissipation of fluid result in the decreased strength and scale of the longitudinal vortex to weaken the heat transfer performance; the vortex strength, vortex core location relative to boundary layer and radius of vortex are all the important parameters for vortex heat transfer performance.

numerical simulation; ribbed channel; structure of vortex; heat transfer

2014-10-09。

费继友(1964—),男,博士后;高铁瑜(通信作者),男,副教授。

国家自然科学基金资助项目(51376028);教育部大学创新研究团队资助项目(IRT1280)。

时间:2015-02-27

10.7652/xjtuxb201505002

TK47

A

0253-987X(2015)05-0007-09

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150227.0845.002.html