Hadoop框架下的多标签传播算法

孙霞,张敏超,冯筠,张蕾,何绯娟

(1.西北大学信息科学与技术学院,710127,西安;2.西安交通大学城市学院,710018,西安)



Hadoop框架下的多标签传播算法

孙霞1,张敏超1,冯筠1,张蕾1,何绯娟2

(1.西北大学信息科学与技术学院,710127,西安;2.西安交通大学城市学院,710018,西安)

标签传播算法的主要思想是利用已标注数据的标签信息预测未标注数据的标签信息。然而,传统传播算法没有区别对待未标注数据与已标注数据相互之间的转移信息,导致算法的收敛速度较慢,影响了算法的性能。针对传统算法的不足,提出了差异权重标签传播算法,算法按标注信息的重要性赋予不同的权重。在解决了大规模特征矩阵相乘问题之后,将提出的差异权重标签传播算法应用到Hadoop框架下,采用分布式计算,实现了能够处理大规模数据的多标签分类算法(HSML),并将提出的HSML算法与现有主流多标签分类算法进行了性能比较。实验结果表明,HSML算法在多标签分类的各项性能评测指标和执行速度上都是有效的。

Hadoop;多标签分类;标签传播算法

传统分类学习问题研究如何将待分类样本准确地划分到唯一的某一类中,即单标签分类。然而,真实世界的对象往往并不只具有唯一的语义。每个对象由多个类别标注,学习的目标是将所有合适的类别标注赋予未见对象,即多标签分类学习。

多标签分类的研究对多义性对象学习模型的建立具有相当重要的意义,现已逐渐成为国际机器学习界一个新的研究热点[1-4]。目前,研究者针对多标签分类问题提出了基于问题转化和基于算法转化的两大类解决方法。问题转化法的主要思想是将多标签分类问题转化为多个单标签分类,再利用已有的单标签分类方法完成分类任务。常见的问题转化法是二元关系法(BR)[5]、标签幂集法(LP)[6]等。与问题转化法不同,算法转化法通过直接改进已有的单标签分类算法进行多标签分类。有多标签K近邻(MLKNN)算法[7]、基于神经网络的反向传播多标签分类算法(BPMLL)[8]、Rank-SVM多标签分类算法[9]等。

多标签学习所面临的最大挑战在于标签空间过大。若一个标签集合具有20个类别,则可能的类别标签集合数将超过一百万(即220)。为了有效应对标注集合空间过大所造成的学习困难,本文提出了分布式学习框架下的多标签分类算法HSML。

1 差异权重的标签传播算法

标签传播算法(LPA)[10]是在2002年由Zhu等人提出的一种基于图的半监督学习方法,其主要思想是利用已标注数据的标签信息来预测未标注数据的标签信息。它首先用数据间的关系建立一个关系完全图,图中节点包含已标注数据和未标注数据,连接两个顶点的边用相似度表示,顶点的标签信息通过转移概率传递给其他相邻顶点,顶点间相似度越大,标签传播的信息也就越多,反复迭代直到收敛。然而,在迭代过程中,传统传播算法没有区别对待未标注数据与已标注数据相互之间的转移信息,导致算法的收敛速度较慢,从而影响了算法的性能。针对传统算法的不足,本文提出了差异权重的标签传播算法。

1.1 算法思想

在传播算法的每次迭代过程中,未标注数据都被重新标注。因此,将这些数据从未标注数据集移到已标注数据集中,与初始标注数据集构成新的标注数据集,指导下次迭代,以达到提高分类准确率的目的。初始标签矩阵F,记为

(1)

式中:FL为已标注标签;FU为未标注标签。标签之间的转移概率矩阵为P,有

(2)

标注转移过程为:FL以PLL的转移子阵向自身转移,FL以PLU的转移子阵向FU转移,FU以PUU的转移子阵向自身转移,FU以PUL的转移子阵向FL转移。由于FL和FU所含的信息量不同,有标签数据向无标签数据转移的信息要比无标签数据之间的相互转移信息重要的多,更比无标签数据向有标签数据转移的信息重要。若对这些不同子阵间的转移不加以区分,会出现少量的真实信息被大量的虚假信息淹没,导致分类效果降低。因此,对于PLU和PUL转移子阵按信息的重要性赋予不同的权重。

1.2 算法描述

差异权重多标签传播算法描述如下。

输入:初始标注训练集XL={(x1,y1),(x2,y2),…,(xl,yl)},未标注训练集XU={x1,x2,…,xu}。

输出:未标注数据的标签FU。

步骤1 依据训练数据建立关系完全图。

步骤4 根据已标注数据初始化标注矩阵F=(FL,FU),其中FU每个分量赋值1/C,依据已标注数据的类标注给相应的FL赋值。

步骤6 从W中选出与xui最近邻的K个已标注样本,如果这K个样本中有K*个样本的标签相同,则转向步骤7,否则转向步骤4中的下一个xui。

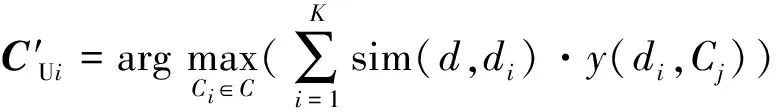
步骤9 把已标注数据的概率分布设置为类的概率值。

步骤10 重复步骤4～9,直到F收敛。

2 HSML算法

若将一个有n(n>5)类别的多标签分类问题中大量的数据计算全部投入到单机上,可能造成计算时间过长或者内存不足,从而引起分类失败。为了有效应对标注集合空间过大所造成的学习困难,本文引入了Hadoop分布式框架[11-12]。Hadoop分布式框架分为Map和Reduce两个部分,Map对一些独立元素进行相应处理,Reduce是对处理结果的一个整合。本文把多标签学习问题分解成多个单标签学习问题,利用Map和Reduce构建2n个单标签分类算法,最后整合各分类的结果,形成最终的多标签分类结果。

2.1 矩阵相乘

本文采用空间向量模型VSM表示每一个样本。若每一个样本用m维特征表示,则样本集大小为n的训练数据可以表示成一个n×m矩阵,通常这样的矩阵具有高维、稀疏的特点,而高维、稀疏矩阵相乘存在耗时长、占用内存高的问题,因此需要寻求高效解决矩阵相乘的方法。

传统的矩阵运算是矩阵A中的每一行分别与矩阵B中的每一列相乘。当矩阵规模增大时,受限于内存大小,一台服务器已经无法处理。稀疏矩阵具有天然可分块特性,出现了许多基于Hadoop的分块矩阵计算方法。算法思想是:将矩阵A中的分块分别与矩阵B相乘,通过Hadoop,每个分块的矩阵相乘可在不同的计算节点完成,最后将结果组合,大大提高了计算速度。

最小粒度相乘算法具有不受限计算节点内存限制的优势,成为矩阵相乘的主流算法。假设有两个超大矩阵A和B,A是一个m×r矩阵,B是一个r×n矩阵,则A中的每个元素Aik与B中第k行元素Bkj依次相乘,计算结果分别为Cij中的一个组成部分;B中的每个元素Bkj与A中第j列元素Aik依次相乘,计算结果分别为Cij的一个组成部分。由于Aik×Bkj是独立的,可由不同计算节点进行运算,最后依据(i,j)(记为key值)将运算结果汇总相加,得到Cij。每个计算节点计算时只加载两个数进行相乘。理论上只要Hadoop的HDFS文件系统足够大,就可以计算任意规模的矩阵相乘。然而在实际操作中,Map的每条输入记录只被处理一次便不再使用。因此,对于矩阵A中的每个元素,进行乘法运算之前,需要生成n个副本;对于矩阵B中每个元素,需要生成m个副本,并将相应位置上的副本相对应。例如,对于Aik需生成n个副本,与B中相应元素对应并以A中元素的行号、B中元素的列号作为key值,矩阵表示为

i-jAik-Bkj

(3)

这种方式势必增加时间复杂度,降低可行性。因此,本文提出了改进的基于Hadoop的最小粒度相乘算法。

2.2 改进的最小粒度相乘算法

由于key值不具备明显的区分度,且Map过程中内存不保留矩阵元素,将数据组织成式(3)格式是极其困难的,在Map输入前查询数据库所耗费的时间也是难以接受的。不难发现,最终结果CiJ是由r个值相加而成的,第k个组成成分为Aik-Bkj。为了使key值更具有区分度,将key值修改为

i-j-kAik,i-j-kBkj

(4)

这样key值所代表的是两个值相乘,得到了Cij中第k个组成元素。矩阵A与矩阵B在Map阶段完成数据副本拷贝后,所有的Map数据记录中i-j-k的key值有且至多有两个。

由于矩阵A中每个元素理论上都需要被计算n遍,矩阵B中每个元素都需要被计算m遍,因此式(4)中有j=1,2,…,k,…,n;i=1,2,…,k,…,m。每个元素的副本拷贝都是独立的,可由不同的Map进行计算,故大大加快了拷贝的速度。

2.3 Hadoop下二元分类器构建

HSML算法是对每个标签构建一个二元分类器,最后再对整个结果进行组合。Hadoop下的二元分类器构建过程如图1所示。

(1)首先对数据集进行特征选择。在后面的实验中,我们使用自建的数据集“Pubmed”,该数据集所处理的对象是文本数据,因此选择词组作为文本特征。通过统计分析,仅提取DT+NN、JJ+NN、JJ+JJ+NN、JJ+JJ+NN+NNS、JJ+NN+NN、NN等形式的名词词组,其中DT是限定词,JJ是形容词,NN是单数名词、NNS是复数名词。然后,采用信息增益的方法计算词特征权重,选择大于阈值的那些词表示数据,同时提取标注数据的标签特征属性,分别得到特征向量矩阵和类别矩阵。

图1 Hadoop下的二元分类器构建过程

(2)第一个MapReduce阶段是进行矩阵计算,完成一次标签传播过程。采用本文提出的改进的最小粒度相乘算法,充分利用分布式计算特点,实现了快速稀疏矩阵相乘。Reducer函数的输出为式(4)的格式。

(3)第二个MapReduce阶段是是采用1.2节提出的差异权重的标签传播算法,对标签数据进行重构。有标签数据向无标签数据转移的信息要比无标签数据之间相互转移的信息重要,更比无标签数据向有标签数据转移的信息重要,因此利用近邻假设,对各概率转移子阵赋予不同的权重。在传播算法过程中,未标注数据被重新标注,并将这些数据从未标注数据集移到已标注数据集中,与初始标注数据集构成新的标注数据集,指导下次迭代。

(4)重复执行上述两个MapReduce过程,直到算法收敛。

(5)将最终结果表示成(标签,数据列表)二元组形式。

(6)对每个标签都执行上述过程,最后整合结果完成多标签分类。

3 实验结果与分析

本实验平台基本配置为HP台式机,Win7、Linux操作系统,Intel酷睿i5处理器,2 GB内存,1 TB硬盘,主要使用Matlab和Java编程语言实现。

3.1 数据集描述

实验釆用Emotions、Image、Yeast和Pubmed 4个数据集。前3个是公开数据集,可从数据堂[13]下载获取,Pubmed是本文构建的数据集。首先向PubMed数据库提交“Lung Cancer”关键字,检索并收集有关肺癌文献摘要,然后提取文献中的MeSH标注作为该文献的标签数据。实验中所使用的数据集基本信息如表1所示。

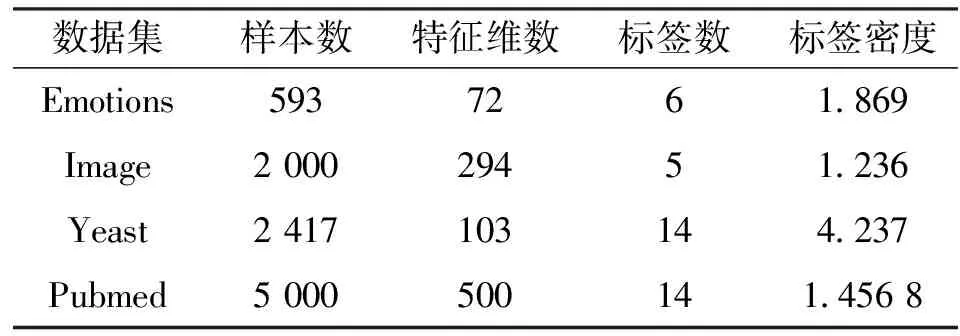
表1 数据集特征描述

3.2 评价指标

本文采用的评价指标有Hamming loss、One-error、Coverage、Ranking loss、Average-precision等。Hamming loss、One-error、Coverage、Ranking loss 4个评价指标的值越小,说明多标签分类器的性能越好,而Average precision的值越大,说明多标签分类器的性能越好。

(1)Hamming loss度量多标签分类器预测出的标签与实际标签之间的差距,即

(5)

(2)One-error度量平均对每个样本的预测标签排序中,排在第一位的标签不在该样本的相关标签集中的概率,即

∉Yi|

(6)

Coverage度量平均对每个样本的预测标签排序中,需要在标签排序列表中最少查找到第几位才可以找出所有与该样本相关的标签,即

(7)

(3)Ranking loss度量所有样本的预测标签排序中,不相关标签排在相关标签前面的平均概率

rankingloss(f)=

(8)

(4)Average precision度量所有样本的预测标签排序中,排在相关标签前面的是相关标签的平均概率,即

(9)

3.3 实验结果

表2对比了本文提出的HSML算法与现有主流多标签分类算法的性能。LIFT、ML-KNN以及BP-MLL算法源代码可从文献[14]下载获取。

由表2可知,HSML算法在Hamming loss指标上稍逊色于LIFT算法、在Coverage上分类性能比BP-MLL稍低以外,在其他指标上均占优势。尤其是对于已标注数据较少的数据集,HSML算法具有明显优势,整体性能优于其他3个算法,充分体现了半监督算法对标注数据量要求不高的优点。

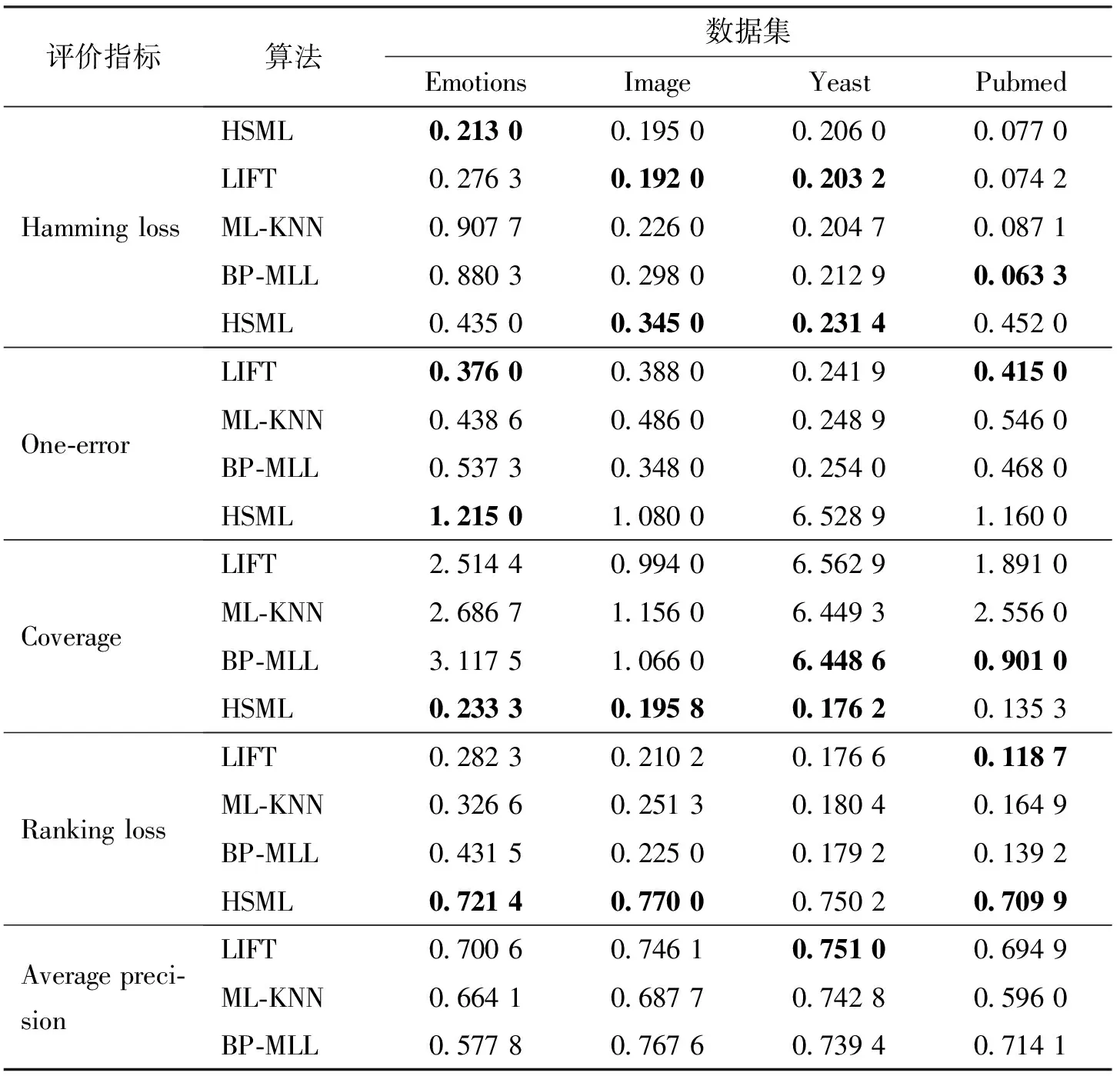
表2 4种多标签算法的分类性能

图2展示了HSML在各数据集上的加速比,从而验证了该算法的执行效率。

图2 HSML在各数据集上的加速比

从图2可以看出,当机器数量越多时,算法的加速比越大,算法的执行效率越高。当只有一台主机时,算法的加速均比小于1,这是因为Hadoop复制数据以及其它内部操作消耗时间,默认将数据备份2份的缘故。数据量越大,随着主机数量增加,其加速比越大,这充分体现了HSML算法的优势,即更易处理大数据。

表3对比了各算法在Pubmed数据集上的训练与测试时间。从表3可知,HSML算法在Pubmed数据集上所花费的时间最少。尤其是与ML-KNN算法相比,HSML算法无论是训练用时还是测试用时都明显较少。这是由于ML-KNN是一种懒惰学习技术,采用在线的方式对测试样本的类标注进行预测,因此计算量大。

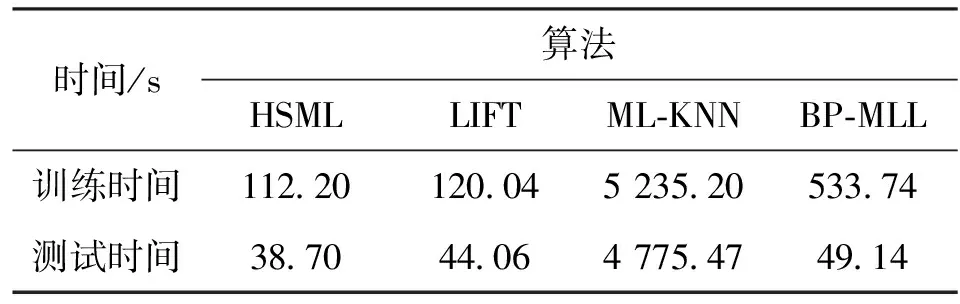
表3 各算法在Pubmed数据集上的训练与测试时间

综上所述,HSML算法具有较好的性能,理论上在主机足够多的情况下,能处理任意规模的大数据计算问题,充分发挥了Hadoop的优越性。

4 总 结

传统的标签传播算法是一种基于流行假设的半监督学习算法,通过迭代将标注信息传递给邻近节点,由于没有区别对待未标注数据与已标注数据相互之间转移信息,导致算法的收敛速度较慢。本文在迭代过程中将标注数据和未标注数据的转移概率按重要程度赋予相应的权重,利用近邻规则的Depuration数据剪辑技术把每次迭代后准确标注的未标注数据加到标注数据,重构标注数据,提出差异权重标签传播算法,从而加快算法的收敛速度,提高算法性能。将多标签学习问题分解成多个单标签学习问题,造成标签空间过大。为了有效应对这一挑战,在解决大规模矩阵相乘问题后,将提出的差别权重标签传播算法应用到Hadoop框架下,使算法能够适应大规模数据多标签分类问题。

[1] ZHANG Minling, ZHOU Zhihua. A review on multi-label learning algorithms [J]. IEEE Transactions on Knowledge & Data Engineering, 2014, 26(8): 1-59.

[2] XU Miao, LI Yufeng, ZHOU Zhihua. Multi-label learning with pro loss [C]∥Proceedings of the 27th AAAI Conference on Artificial Intelligence. Palo Alto, California, USA: AAAI, 2013: 998-1004.

[3] SUN Y Y, ZHANG Y, ZHOU Z H. Multi-label learning with weak label [C]∥24th AAAI Conference on Artificial Intelligence. Palo Alto, California, USA: AAAI, 2010:593-598.

[4] 孔祥南, 黎铭, 姜远, 等. 一种针对弱标记的直推式多标记分类方法 [J]. 计算机研究与发展, 2010, 47(8): 1392-1399. KONG Xiangnan, LI Ming, JIANG Yuan, et al. A transductive multi-label classification method for weaklabeling [J]. Journal of Computer Research and Development, 2010, 47(8): 1392-1399.

[5] BOUTELL M R, LUO J, SHEN X, et al. Learning multi-label scene classification [J]. Pattern Recognition, 2004, 37(9): 1757-1771.

[6] TSOUMAKAS G, VLAHAVAS I. Random k-labelsets: an ensemble method for multilabel classification [C]∥18th European Conference on Machine Learning. Berlin, Germany: Springer, 2007: 406-417.

[7] ZHANG Minling, ZHOU Zhihua. ML-kNN: a lazy learning approach to multi-label learning [J]. Pattern Recognition, 2007, 40(7): 2038-2048.

[8] ZHANG Minling, ZHOU Zhihua. Multilabel neural networks with applications to functional genomics and text categorization [J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18(10): 1338-1351

[9] ELISSEEFF A, WESTON J. A kernel method for multi-labelled classification [C]∥Advances in Neural Information Processing Systems. Cambridge, MA, USA: MIT, 2002: 681-687.

[10]ZHU X J, GHAHRAMANI Z. Learning from labeled and unlabeled data with label propagation, CMU-CALD-02-107 [R]. Pittsburghers, USA: Carnegie Mellon University, 2002.

[11]Welcome to Apache [EB/OL]. [2013-10-14]. http:∥hadoop.apache.org.

[12]Hadoop 集群安装 [EB/OL]. [2013-12-20]. http:∥blog.csdn.net/liou825/article/details/9320745.

[13]数据堂 [EB/OL]. [2014-04-01]. http:∥www.datatang.com/data/list.

[14]张敏灵个人主页 [EB/OL]. [2014-04-01]. http:∥cse.seu.edu.cn/people/zhangml/Publication.htm.

[本刊相关文献链接]

马莉,唐善成,王静,等.云计算环境下的动态反馈作业调度算法.2014,48(7):77-82.[doi:10.7652/xjtuxb201407014]

陈秀真,李生红,凌屹东,等.面向拒绝服务攻击的多标签IP返回追踪新方法.2013,47(10):13-17.[doi:10.7652/xjtuxb 201310003]

刘光辉,任庆昌,孟月波,等.自适应先验马尔可夫随机场模型的图像分割算法.2013,47(10):62-67.[doi:10.7652/xjtuxb201310011]

杜友田,辛刚,郑庆华.融合异构信息的网络视频在线半监督分类方法.2013,47(7):96-101.[doi:10.7652/xjtuxb201307 018]

艾波,胡军,张早校,等.含缺陷蒸汽发生器管道爆破压力预测的遗传-神经网络算法.2011,45(9):84-89.[doi:10.7652/xjtuxb201109016]

徐胜军,韩九强,赵亮,等.用于图像分割的局部区域能量最小化算法.2011,45(8):7-12.[doi:10.7652/xjtuxb201108 002]

温超,耿国华,李展.构建新包空间的多示例学习方法.2011,45(8):62-66.[doi:10.7652/xjtuxb201108011]

余思,桂小林,黄汝维,等.一种提高云存储中小文件存储效率的方案.2011,45(6):59-63.[doi:10.7652/xjtuxb201106 011]

(编辑 赵炜)

A Label Propagation Algorithm for Multi-Label Classification Using Hadoop Technology

SUN Xia1, ZHANG Minchao1, FENG Jun1, ZHANG Lei1, HE Feijuan2

(1. School of Information and Technology, Northwest University, Xi’an 710127, China; 2. Department of Computer Science, Xi’an Jiaotong University City College, Xi’an 710018, China)

A method of label propagation using Hadoop technology, named HSML, is proposed, to cope with the challenge of exponential-sized output space learning from multi-label data. Label propagation algorithms are graph-based semi-supervised learning methods, and use the label information of labeled data to predict the label information of unlabeled data. Traditional label propagation algorithms do not consider the posterior probability and distinguish information between labeled data and unlabeled data during the label propagation process, hence, the performance of traditional label propagation algorithms is affected. Therefore, a label propagation algorithm with different weights is proposed. After the multiplication problem of large-scale feature matrices is solved, the proposed algorithm is applied to the framework of Hadoop to deal with the problem of multi-label classification learning from big data. Experimental results and comparisons with some well-established multi-label learning algorithms, show that the performance of HSML is superior, and that the bigger test set is the faster HSML runs.

Hadoop; multi-label classification; label propagation algorithm

2014-11-18。

孙霞(1977—),女,副教授。

国家自然科学基金资助项目(61202184,61100166);陕西省教育厅资助项目(2013JK1152)。

10.7652/xjtuxb201505021

TP391

A

0253-987X(2015)05-0134-06