大型风电场动态等值的改进支持向量聚类算法
滕卫军,王锡凡,石文辉
(1.西安交通大学电气工程学院,710049,西安;2.中国电力科学研究院,100192,北京)
大型风电场动态等值的改进支持向量聚类算法
滕卫军1,王锡凡1,石文辉2
(1.西安交通大学电气工程学院,710049,西安;2.中国电力科学研究院,100192,北京)
针对风速波动性强与风电场多样性导致的风机聚类参数多样化的特点,提出了一种基于支持向量聚类(SVC)的大型风电场动态等值聚类算法。该算法应用遗传算法实现簇标定,采用分段多目标函数迭代求解,保证了聚类结果的精度与速度,克服了传统SVC簇标定抽样判决的不足。应用样本轮廓值修正聚类结果,保证聚类结果的合理性,根据等值前后风机机端电压不变原则建立了电缆等值模型。以实际风电场为算例进行仿真,结果表明,该算法单次聚类时间为SVC的4%左右,采用遗传算法能够实现不同精度的等值机台数优化,得到的等值机与簇内单机的有功功率、无功功率动态特性具有较高一致性,轮廓值修正能够保证聚类结果的样本轮廓值都大于0。
大型风电场;动态等值;支持向量聚类;遗传算法;分段多目标函数
随着风电大规模入网,大型风电场并网对电力系统的影响日益受到人们的关注[1-2]。一般大型风电场包含数百台风机,进行电力系统动态特性研究时,建立风电场的详细模型会大大增加系统模型的复杂度和计算仿真时间[3-4],因此,有必要研究保证动态特性精度的大型风电场动态等值技术[5-6]。目前,风电场动态等值方法主要有单机等值法和多机等值法[7-9]。单机等值法假设风机输入风速相同,风电场等值为一台风机;多机等值法将运行点相近的风机等值为一台风机,风电场等值为多台风机。受尾流效应和风机轴系的影响,为提高动态等值精度,风电场动态等值广泛采用多机等值法[10]。
目前已有较多的国内外文献对风电场动态等值技术进行了研究。文献[2]给出了装有绕线式异步风机和双馈式感应风机风电场的等值模型,将风电场等值为一台容量为单台风机之和的大容量风机。文献[3]采用支持向量技术,基于历史风速数据建立了适用于风电场一年风况的多机等值模型,前提是假设风速相同的风机动态特性相同。文献[7-8]给出了含定速和变速风机的风电场等值模型,并考虑了风速差异。文献[9]应用遗传算法,对发电机的电气参数进行遗传算子操作,得到了风电场单机等值模型。文献[4]应用聚类算法建立了含双馈风机风电场的等值模型。文献[11-14]研究了尾流效应对风电场风机风速的影响,得出不考虑尾流效应的风电场模型会产生较大误差的结论。文献[15]建立了变速变桨控制风机的风电场等值模型,能够模拟风速波动下的风电场特性。
风机聚类算法广泛采用k-means算法,该方法过程简单,实现方便,但需预先设定聚类簇数和选择初始聚类点[16],一般事先无法确定合适的聚类簇数与初始聚类点。风速波动性较强与风电场结构多样导致风机聚类参数的多样性,故风电场风机聚类算法要适应不同风况下的聚类。支持向量聚类(SVC)算法[17-21]具有对数据形状无要求、能形成任意形状簇等优点,可以更好地处理不同风况下的风机聚类。但是,支持向量聚类技术的簇标定会耗费大量时间,虽然已有很多文献对簇标定进行了研究,但除文献[21]外,其他算法都采用了抽样判决模式,以标定错误换取时间的提升。
遗传算法具有求解灵活、多点求解、适合处理离散变量等优点。针对存在的问题,本文提出了一种基于遗传算法(GA)实现簇标定的SVC优化聚类算法,该算法利用GA分段多目标函数实现簇标定,保证了聚类的精度和速度,克服了支持向量技术簇标定抽样判决造成的计算量大和易于产生误差的不足,并且可以在不预设等值机台数的条件下优化不同聚类精条件的等值机台数。应用轮廓值修正聚类结果,使样本轮廓值大于0,保证聚类结果的合理性,同时根据等值前后风机机端电压不变原则建立了风电场电缆等值模型。以风机动态方程状态变量为聚类指标,在电力系统分析软件DIgSILENT/PowerFactory中对大型风电场进行动态等值的仿真研究,结果表明了本文所提聚类方法的正确性和优越性。
1 SVC-GA优化聚类算法
1.1 SVC轮廓提取
给定数据集{x1,x2,…,xN},xi∈Rn。设a是特征空间中最小超球体球心,R是超球体半径,ξi是松弛因子,Φ是从原空间到特征空间的非线性映射,SVC优化目标函数为
s.t. ‖Φ(xi)-a‖2≤R2+ξi,ξi≥0
(1)
将式(1)转化为Lagrange函数形式,对R、a和ξi分别求偏导,根据KTT条件,消去R、a和ξi,最终目标函数简化为

(2)
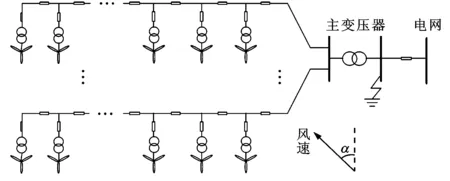
求解式(2),根据拉格朗日乘子判断数据位置,βi=0对应的点位于超球体内,称为内部向量;0<βi 以上SVC优化阶段得到了描述数据簇轮廓的支持向量。SVC支持向量形成的簇轮廓形状任意,是该算法最突出的优点,能够适用于不同风况的风电机组聚类。 1.2 SVC簇标定改进方法 由于遗传算法可以实现多点求解、求解灵活以及适用于离散变量求解等特点,本文采用遗传算法实现簇标定:首先所有支持向量单独成簇,采用式(3)分段多目标函数,应用遗传算法迭代求解。具体过程为 (3) 式中:nc为簇数;ρ为各簇数据方差之和;α为权重系数;K为迭代次数;M为预设的正整数。 本文根据支持向量之间的相似性形成染色体,染色体长度为支持向量个数,每个基因对应一个支持向量,基因值为距离该位置支持向量最近的支持向量号,遗传操作迭代时,只将该位置支持向量交叉或者变异到距离其最近的支持向量所在簇,从而保证聚类精度,并提高求解速度。支持向量聚类后,将非支持向量归入距离其最近的支持向量所在簇,计算第i次遗传操作各染色体的目标函数,继续下次遗传操作迭代。为了保证求解质量,每次迭代按目标函数值,保留一定数量的最优染色体不参与交叉变异操作。 由于遗传算法本身无法保证得到最优解与所有数据的轮廓值都大于0,所以本文根据轮廓值对遗传算法得到的分群结果进行修正,保证所有样本的轮廓值都大于0。样本轮廓值计算表达式为[4] (4) 式中:a为样本i与同簇其他样本之间的平均距离;b为向量,样本i与不同簇的簇内样本之间的平均距离。轮廓值S(i)取值范围为[-1,1],S(i)越大样本i分类越合理,S(i)<0则样本i分类不合理。 本文算法步骤为:①SVC计算支持向量,应用遗传算法对支持向量进行聚类;②将非支持向量归入距离其最近支持向量所在簇;③应用轮廓值对数据进行修正,保证数据的轮廓值都大于0,并重复上述过程,直到达到收敛条件。 1.3 分群指标 尾流效应导致风电机组运行状态不同[12-13],故对风电机组分群需要选择能够反映其动态特性的聚类参数。本文风电场等值研究的是系统侧发生短路故障条件下的风电场动态特性,根据风电机组动态方程,选取动态方程的状态变量作为聚类指标。 第i台风机的定转子电流分量以及转速作为该风机的状态向量xi,所有风机的状态向量组成状态向量组X=[x1,x2,…,xN]T,N为风电场风机台数,作为支持向量聚类技术的输入。 风电场等值需要等值的元件包括发电机、变压器、风电场内部电缆/架空线等。本文发电机、机端变压器等值参数求解采用容量加权法[4],计算公式为 (5) 式中:S、P分别为风机额定容量与额定功率;变量r、x分别表示电阻和电抗;下标s、r和m分别表示定子、转子和励磁;H、K、D分别为惯性时间常数、轴系刚度系数和轴系阻尼系数;n为风电机组数等值机台数。 实际风电场分布较广,风机距离风电场出口(PCC)电气距离不同,如图1所示,需要对风电场电缆进行等值。本文以等值前后风机端电压不变为等值原则,建立风电场电缆的等值模型,保证等值机到PCC电压降不变。为计算风机与PCC之间电缆的阻抗,有 (6) 式中:I、Ir和Ii分别为机端的电流幅值、实部和虚部;ΔUr、ΔUi分别为机端到PCC的压降实部和虚部均值;Req、Xeq分别为等值电阻和电抗。 图1 实际风电系统内部接线图 3.1 算例说明 本文风电场包含12条馈线,共133台双馈式风电机组,风机经箱变和箱变侧电缆连接到各回馈线,然后经过主变压器升压至330 kV,最后经输电线路连接至电网330 kV母线,如图2所示。 图2 风电场接线图 假设风电场风速为10.5 m/s,风向50°。由于故障时间较短(本文故障时间设为0.1 s),故可假设故障期间风电场风速不变。通过查找风电场风速分布因子表,得到的风机输入风速如图3所示。 图3 风机输入风速 本文遗传算法种群数设为70,变异率为0.02,交叉率为0.2,并保留15%的最优染色体。 3.2 聚类结果 采用遗传算法可得到多个聚类结果,本文给出了其中的24台和6台等值机的聚类和仿真结果,与单机等值模型一起,分别用场景1、2、3表示。场景1和2的聚类结果如表1、2所示。本文算法可以得到多个不同精度、不同等值机台数的聚类结果,因此,可以根据具体的应用场合与精度要求选择等值场景。 表1 聚类结果1 表2 聚类结果2 聚类结果1、2的样本轮廓值如图4所示。 图4 样本轮廓值 由图4可知,两种聚类结果所有样本的轮廓值都大于0,说明了本文方法所得聚类结果的合理性。 3.3 仿真结果 图5为风电场主变压器高压侧发生三相接地短路故障时,场景1等值机及簇内单机的动态特性曲线,为显示清晰,图中只给出了一台等值机。图中实线、虚线分别为等值机和簇内单机动态特性曲线(等值机有功或无功功率除以簇内机组数)。由图可知,等值机动态特性曲线位于其簇内单机有功、无功功率特性曲线簇内,说明等值机可以较好地代替簇内机组。 表3给出了详细模型以及场景1、2、3的仿真时间和基于本文聚类算法原理得到的单次聚类时间。由表3可知,场景1、2、3的仿真时间分别为详细模型的15.45%、3.33%和1.69%,因此风电场等值模型可大大提高系统仿真效率,且等值机台数越少,运行效率越高。结合表1、表2和图6可知,等值机台数减少,等值机变量与簇内单机变量误差增大,等值精度降低,因此需要根据实际精度要求选择风电场等值机台数。3种场景下,基于本文聚类算法得到的单次聚类时间分别是基于SVC聚类算法时间的4.00%、6.47%和2.66%,因此本文聚类算法可以快速得到指定簇数的聚类结果。 表4为本文算法与SVC算法得到的6台等值机结果对比。由表4可知,本文算法得到的等值结果簇内数据到簇中心距离方差小于SVC算法,说明本文算法可以更好地实现分群聚类。 表3 仿真结果对比 表4 各簇数据到簇中心距离均值 (a)有功功率 (b)无功功率图5 场景1第一台等值机输出变量曲线 (a)有功功率 (b)无功功率图6 主变压器低压侧动态特性 图6给出了主变压器高压侧发生三相短路故障时风电场有功功率、无功功率的动态特性曲线。由图6可知,场景1等值模型主变压器低压侧有功与无功功率的动态特性与详细模型几乎一致,场景2比场景1精度差,因此本文方法建立的风电场等值模型可以保证风电场主压器低压侧有功和无功功率动态精度。 本文提出了一种基于SVC-GA的风电场动态等值优化聚类优化方法,该算法利用GA实现簇标定,分段目标函数保证聚类精度和速度,实现了不同聚类精度下优化等值机台数,避免了抽样判决计算量大和容易产生聚类误差的不足。应用样本轮廓值修正遗传算法聚类结果,保证聚类结果合理性,并将非支持向量归入其距离最近簇。与传统SVC相比,本文算法大大减少了单次聚类时间。研究表明,等值场景1、2、3可大大减少系统的仿真时间,提高仿真效率,且等值机台数越少,仿真时间就越短,但同簇单机动态特性相似度降低。本文采用GA可得到不同精度条件下优化的风电场等值模型,因此可以根据风电场动态等值精度要求选择风电场等值模型。 根据等值前后风机机端与PCC点之间压降不变原则,建立了风电场的电缆等值模型。研究表明,本文风电场电缆等值模型可以保证等值机机端电压与簇内单机机端电压具有较高的一致性,能够提高等值机的动态等值精度,说明了本文电缆等值方法的正确性。 [1] AHMAD S D, MAHMUD F F. A reliability model of large wind farms for power system adequacy studies [J]. IEEE Trans on Energy Conversion, 2009, 24(3): 792-801. [2] FERNANDEZ L M, GARCIA C A, SAENZ J R, et al. Equivalent models of wind farms by using aggregated wind turbines and equivalent winds [J]. Energy Conversion and Management, 2009, 50(3): 691-704. [3] MUHAMMAND A, ILIE I S, MILANOVIC J V, et al. Wind farm model aggregation using probabilistic clustering [J]. IEEE Trans on Power Systems, 2013, 28(1): 309-316. [4] 陈树勇, 王聪, 申洪, 等. 基于聚类算法的风电场动态等值 [J]. 中国电机工程学报, 2012, 32(4): 11-19. CEHN Shuyong, WANG Cong, SHEN Hong, et al. Dynamic equivalence for wind farms based on clustering algorithm [J]. Proceedings of the CSEE, 2012, 32(4): 11-19. [5] TRUDNOWSKI D J, GENTILE A, KHAN J M, et al. Fixed-speed wind-generator and wind-park modeling for transient stability studies [J]. IEEE Trans on Power Systems, 2004, 19(4): 1911-1917. [6] CHOWDHURY M A, SHEN W X, HOSSEINZADEH N, et al. A novel aggregated DFIG wind farm model using mechanical torque compensating factor [J]. Energy Conversion and Management, 2013, 67(3): 265-274. [7] FERNANDEZ L M, SAENZ J R, JURADO F. Dynamic models of wind farms with fixed speed wind turbines [J]. Renewable Energy, 2006, 31(8): 1203-1230. [8] FERNANDEZ L M, JURADO F, SAENZ J R. Aggregated dynamic model for wind farms with doubly fed induction generator wind turbines [J]. Renewable Energy, 2008, 33(1): 129-140. [9] LI H, YANG C, ZHAO B, et al. Aggregated models and transient performances of a mixed wind farm with different wind turbine generator systems [J]. Electric Power Systems Research, 2012, 92(11): 1-10. [10]AKHMATOV V, KNUDSEN H. An aggregate model of a grid-connected, large-scale, offshore wind farm for power stability investigations: importance of windmill mechanical system [J]. Electrical Power and Energy Systems, 2002, 24(9): 709-717. [11]HE Yikang, HU Jiabing, ZHAO Rende. Modeling and control of wind-turbine used DFIG under network fault condition [C]∥Proceedings of the 8th International Conference on Electrical and Systems. Piscataway, NJ, USA: IEEE, 2005: 986-991. [12]曹娜, 于群. 风速波动情况下并网风电场内风电机组分组方法 [J]. 电力系统自动化, 2012, 36(2): 42-46. CAO Na, YU Qun. A grouping method for wind turbines in a grid-connected wind farm during wind speed fluctuation [J]. Automation of Electric Power System, 2012, 36(2): 42-46. [13]ALI M, MATEVOSYAN J, MILANOVIC J V, et al. Effect of wake consideration on estimated cost of wind energy curtailments [C]∥8th International Workshop on Large Scale Integration of Wind Power into Power Systems as Well as on Transmission Networks for Offshore Wind Farms. Bremen, Germany: Wind Integration Workshop, 2009: 14-15. [14]曹娜, 赵海翔, 任普春, 等. 风电场动态分析中风速模型的建立及应用 [J]. 中国电机工程学报, 2007, 27(36): 68-72. CAO Na, ZHAO Haixiang, REN Puchun, et al. Establish and application of wind speed model in wind farm dynamic analysis [J]. Proceedings of the CSEE, 2007, 27(36): 68-72. [15]TOMMASI L D, GIBESCU M, BRAND A J. A dynamic wind farm aggregate model for the simulation of power fluctuation due to wind turbulence [J]. Journal of Computational Science, 2010(1): 75-81. [16]米增强, 苏勋文, 杨奇逊, 等. 风电场动态等值模型的多机表征方法 [J]. 电工技术学报, 2010, 25(5): 162-169. MI Zengqiang, SU Xunwen, YANG Qixun, et al. Multi-machine representation method for dynamic equivalent model of wind farms [J]. Transactions of China Electrotechnical Society, 2010, 25(5): 162-169. [17]HUR A B, HORN D, SIEGELMANN H T, et al. Support vector clustering [J]. Journal of Machine Learning Research, 2001(2): 125-137. [18]LEE J, Lee D. An improved cluster labeling method for support vector clustering [J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(3): 461-464. [19]CHIANG J H, HAO P Y. A new kernel-based fuzzy clustering approach: support vector clustering with cell growing [J]. IEEE Transactions on Fuzzy Systems, 2003, 11(4): 518-527. [20]YANG J H, ESTIVILL-CASTRO V, CHALUP S K. Support vector clustering through proximity graph modeling [C]∥Proceedings of the 9th International Conference on Neural Information Processing. Piscataway, NJ, USA: IEEE, 2002: 552-559. [21]LEE S H, DANIELS K M. Cone cluster labeling for support vector clustering [C]∥ Proceedings of 6th SIAM Conference on Data Mining. Philadelphia, USA: SIAM, 2006: 151-162. (编辑 赵炜) An Improved Support Vector Clustering Algorithm for the Dynamic Equivalence of Large Wind Farms TENG Weijun, WANG Xifan, SHI Wenhui (1. School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. China Electric Power Research Institute, Beijing 100192, China) A clustering algorithm to the dynamic equivalent of large wind farms based on SVC is proposed to deal with the diversity of clustering parameter of wind turbines due to the variant of wind energies and the diversity of layout of wind farms. A genetic algorithm is used to realize clustering assignments. Piecewise multi-objective functions are used for iterative solution to ensure the speed and accuracy of clustering results, and to overcomes the disadvantage of traditional SVCs in clustering assignments. Outlier values of samples are used to modify the clustering results and to ensure the rationality of clustering results. An equivalent model for cables is built based on the principle that the terminal voltage of wind turbines keeps unchanged. Simulation results of a real wind farm show that the clustering time of the proposed method is about 4%of SVC. The proposed clustering method based on GA optimizes the number of equivalent wind turbines under different accuracies. The dynamic characteristics such as active power and reactive power of equivalent wind turbines are highly consistent with those of individual wind turbines in the cluster. Modification using outlier values ensures that all the outlier values of wind turbines are greater than 0. large wind farm; dynamic equivalent; support vector clustering; genetic algorithm; segmented multi-objective function 2014-09-19。 滕卫军(1987—),男,博士生;王锡凡(通信作者),男,教授,博士生导师,中国科学院院士。 国家电网公司科技资助项目(NY71-13-008)。 时间:2015-03-03 10.7652/xjtuxb201505015 TH-39 A 0253-987X(2015)05-0094-06 网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150303.1110.005.html2 等值元件参数计算

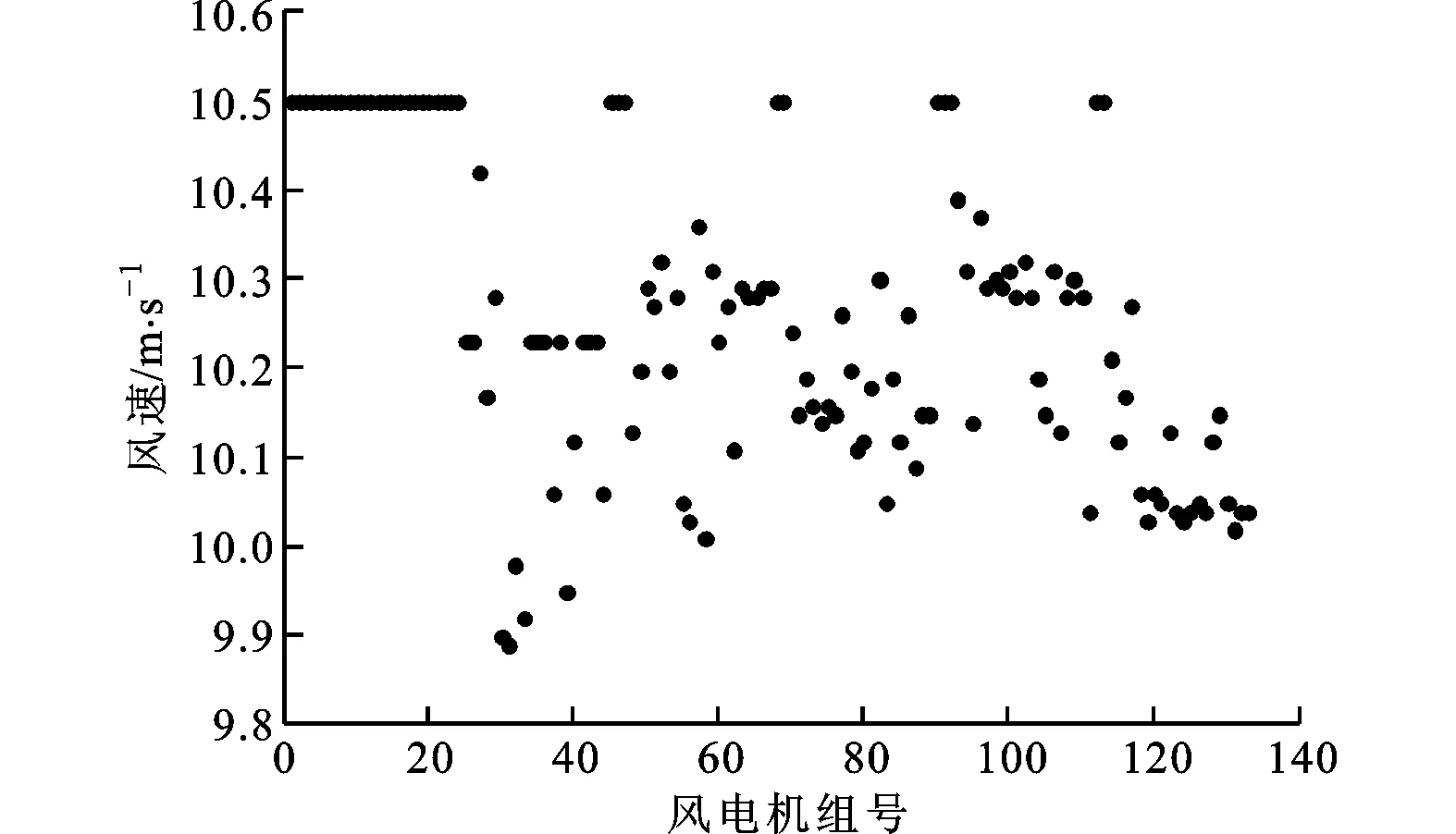
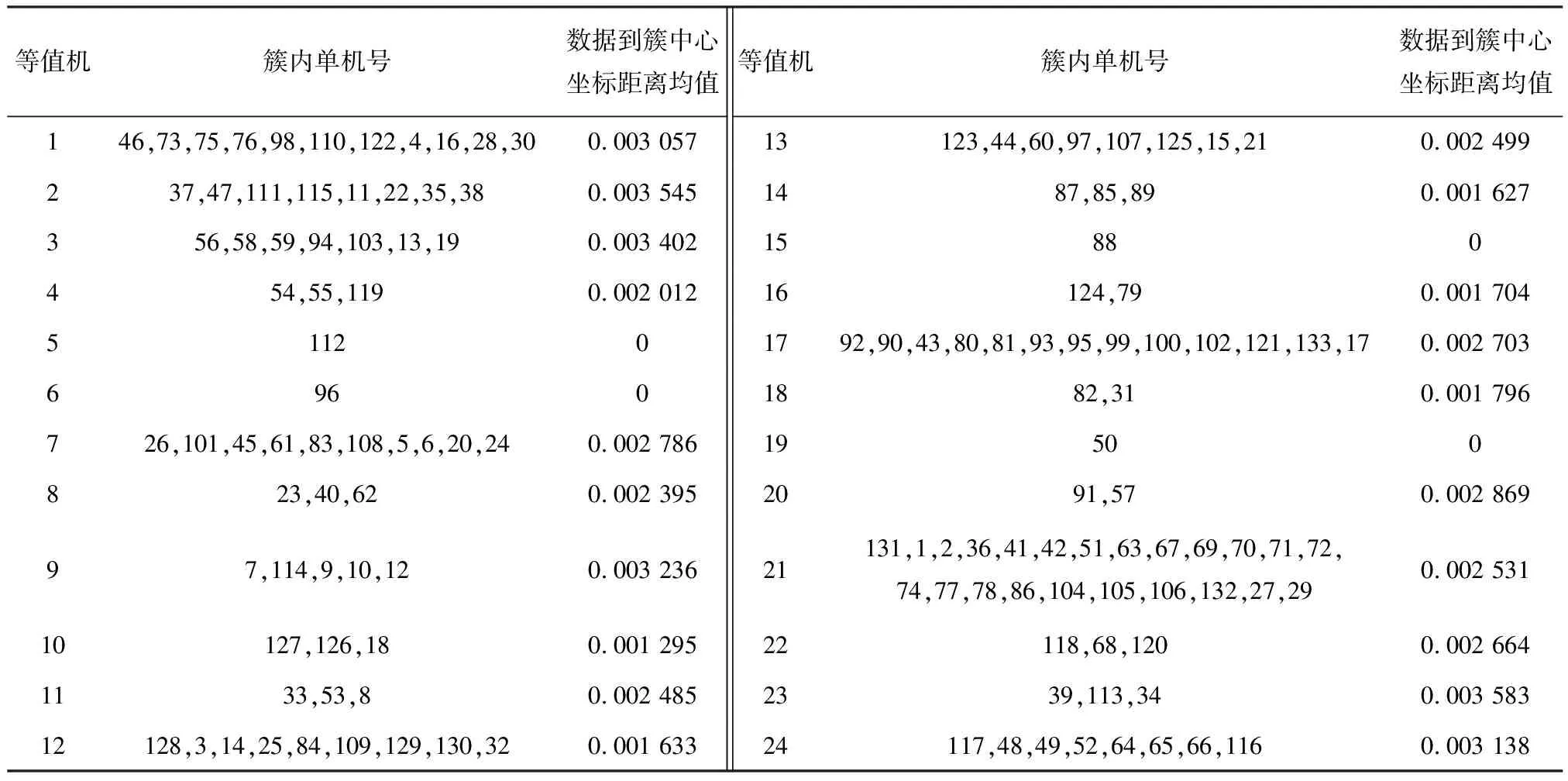
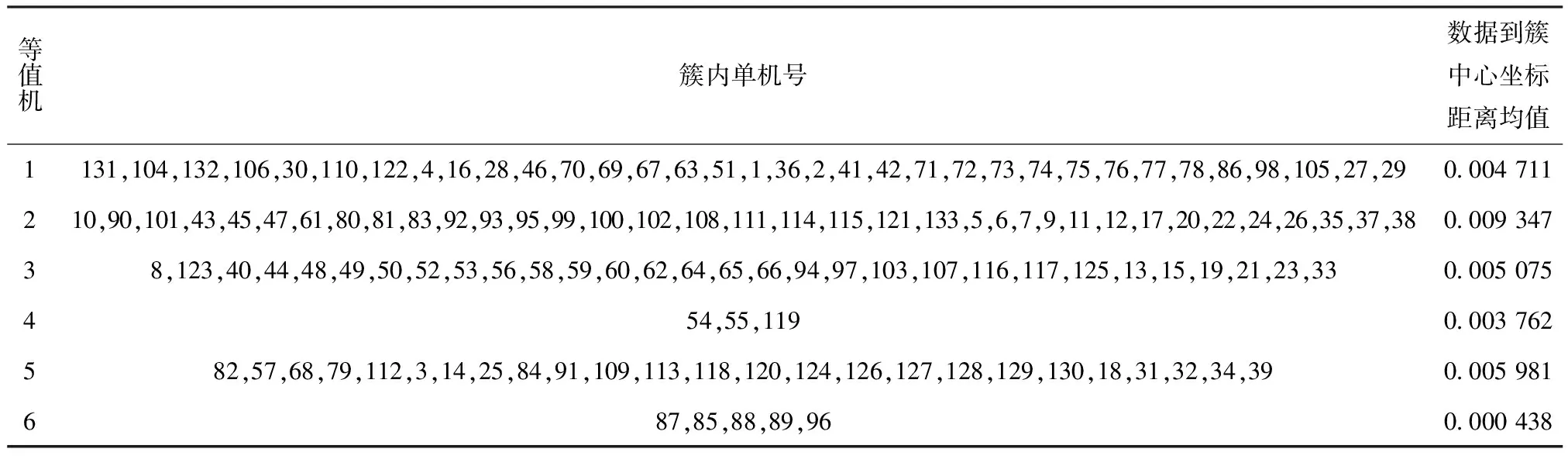
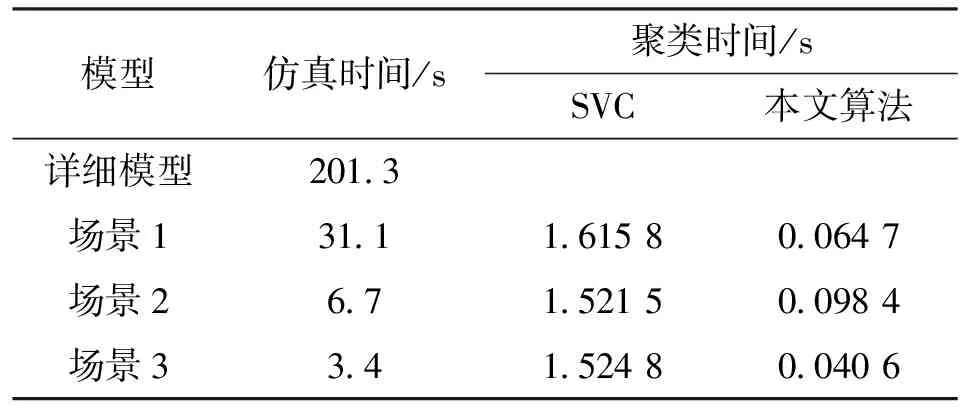
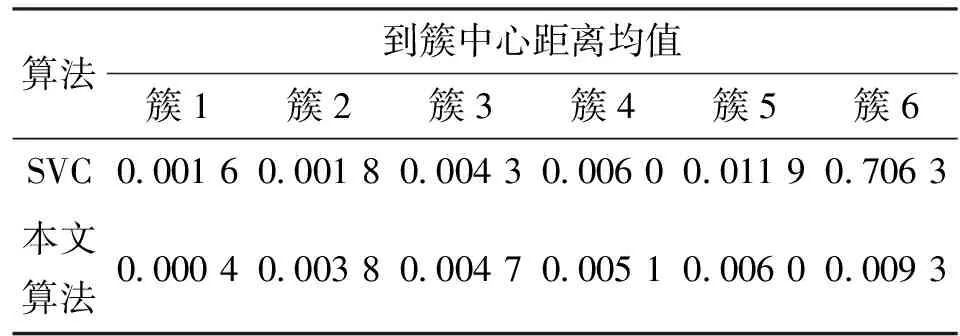
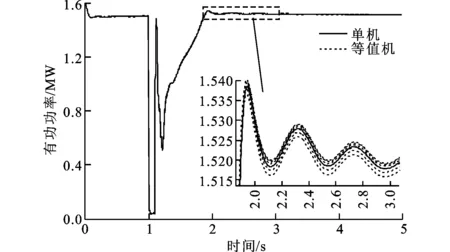
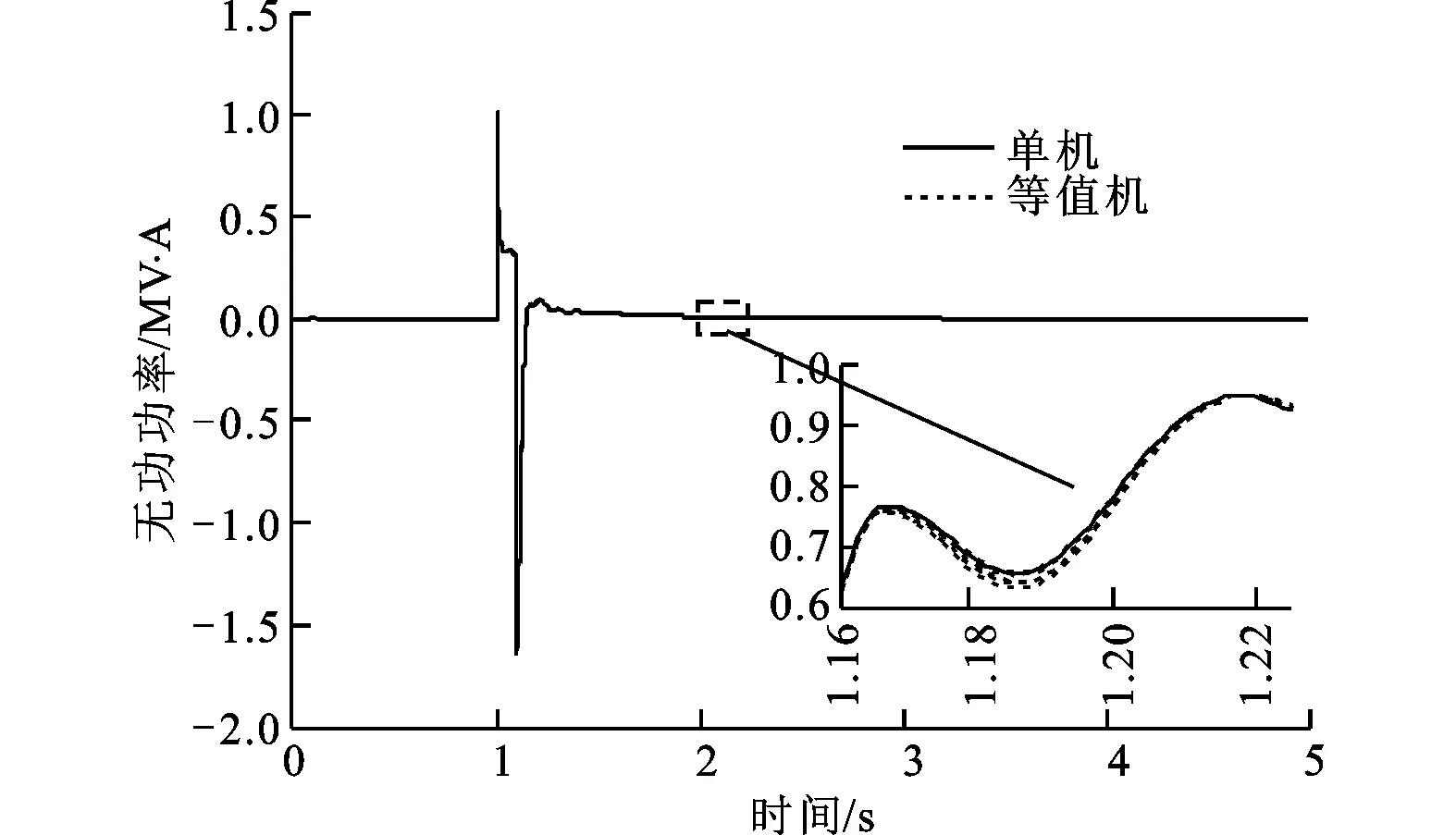
3 仿真研究

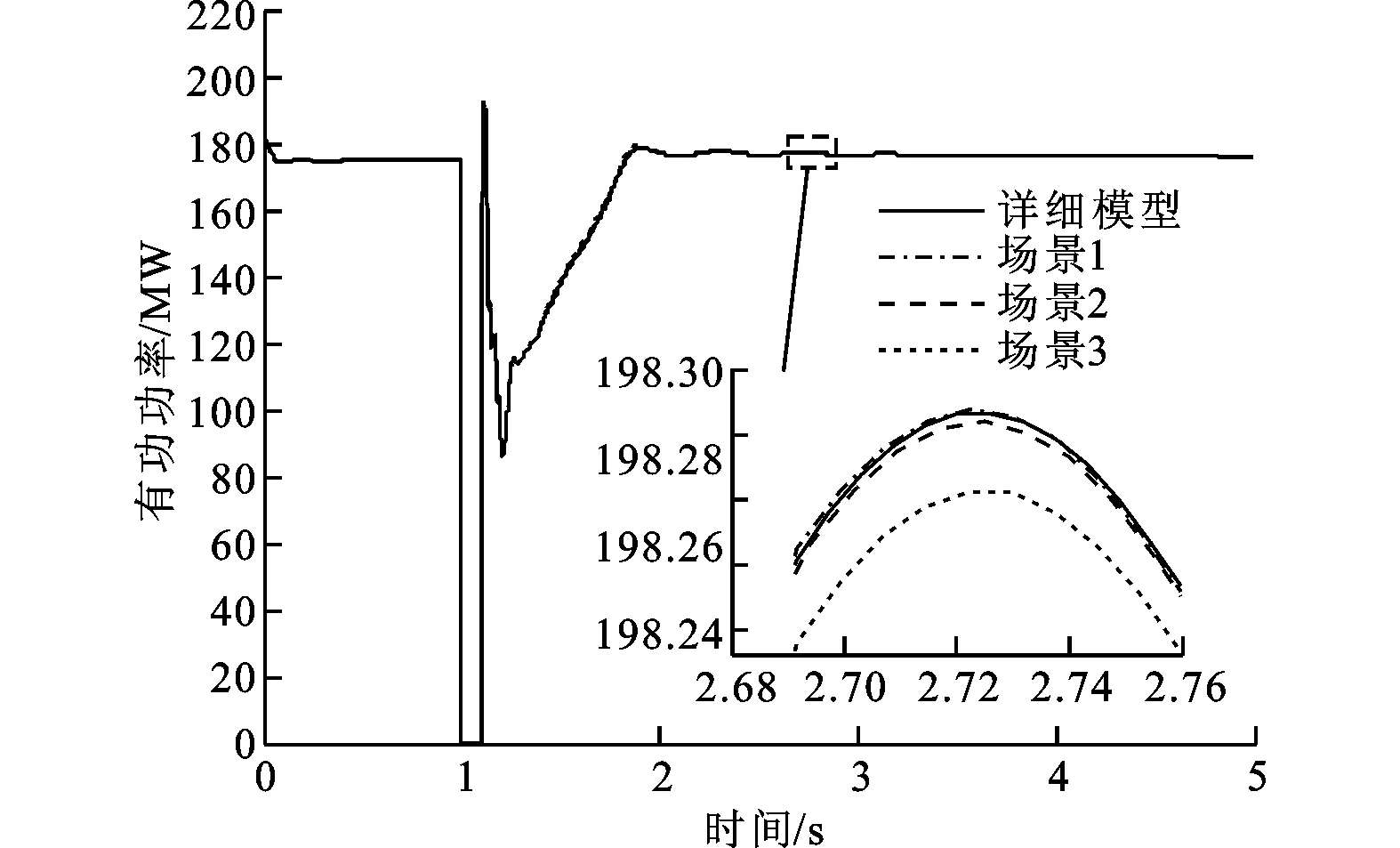
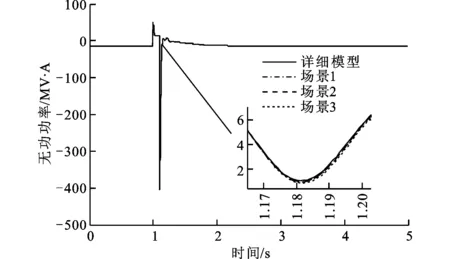
4 结 论

