交流伺服系统永磁同步电机电流及位置二级状态观测器设计

郝双晖,王磊,宋宝玉,郝明晖

(哈尔滨工业大学机电工程学院,150001,哈尔滨)



交流伺服系统永磁同步电机电流及位置二级状态观测器设计

郝双晖,王磊,宋宝玉,郝明晖

(哈尔滨工业大学机电工程学院,150001,哈尔滨)

为了提高交流伺服控制系统的反馈精度,并消除反馈信号的滞后问题,针对永磁同步电机电压控制模型及其运动学控制模型进行深入分析,并在此基础上对控制系统反馈环节的工作时序进行分析,得到了电流及位置反馈环节的滞后周期数,提出电流及位置一级状态观测器。通过当前控制周期反馈位置及电流值,对下一个控制周期的电流及反馈位置值进行精确估计,并将一级状态观测器的观测输出值作为二级状态观测器的输入,进一步抑制电流及位置反馈信号的高频振荡及时滞。结果表明:二级电流及位置状态观测器对反馈信号的高频噪声起到明显的抑制作用,并对反馈值进行了准确的预计观测;二级位置观测误差小于0.005 rad,并消除了反馈中夹杂的高频噪声。将该方法应用于交流伺服控制系统中,进行高速高响应定位控制,响应频率达到200 Hz,加速度达到62 831 rad/s2,此时系统相电流稳定,定位精度达到1.5°,从而实现了电流及位置的精确观测。

永磁同步电机;电压控制模型;状态观测器

精确可靠的反馈环节是实现高性能伺服控制的前提。电流传感器采样电机三相电流时会引入系统噪声,伺服控制计算的工作时序也会造成电流采样值的延时,引起控制系统的振荡[1]。角度反馈是实现伺服闭环控制的重要环节,角度精度影响着伺服系统的控制精度。因此,如何得到精确可靠的反馈环节是实现高精度高响应伺服控制的必要条件。

在编码器角度检测研究方面,无传感器伺服控制得到了广泛研究,但是该控制无法满足高精度以及在复杂工作环境下工作的要求[2]。虽然光电编码器精度高、电磁噪声抑制能力强,但光电编码器体积大、无法在振动剧烈的环境下工作,而磁电编码器则具有抗冲击能力强、可靠性高的特点[3]。

在电流检测研究方面,文献[4]利用电流互感器、运算放大器和可调电阻搭建了电流检测电路,充分考虑了电压跟随以及电压抬升过程的问题,实现了电流的精确检测。文献[5]针对永磁同步电动机相电流检测原理和采样时间的要求,采用一种基于单电阻采样方式的电动机相电流重构法,实现电流的高精度检测。

文献[6]提出磁电编码器的标定查表法,利用高精度光电编码器对磁电编码器的角度值进行标定修正,提高了磁电编码器的精度。文献[7]设计了一种基于状态观测器的磁电编码器解调算法,具有较强的干扰抑制能力。文献[8]利用二进制数列实现了磁电编码器绝对位置的计算,并提出了线性化反馈移位寄存器,用于实现磁电编码器的整周最细分割和提高磁电编码器的分辨率。文献[9]依据二自由度转向动力学模型建立了Kalman滤波模型,并设计了位置状态观测器,提高了角度观测精度,并有效抑制了噪声信号。文献[10]基于Lyapunov稳定性理论,利用线性不等式-LMI技术,实现了位置状态误差的逐渐收敛,提高了反馈角度精度。文献[11]基于傅里叶变换方法引入编码器的校正传递函数,实现了编码器的高精度观测。

本文基于控制系统的电压控制模型和电机转子运动模型,设计了电流环及位置环状态观测器,介绍并分析了交流伺服控制系统的工作时序及电流环、位置环状态观测器的设计过程,并进行了电流及位置观测实验,实验结果表明了该方法的有效性。

1 磁场定向控制

1.1 永磁同步电机模型

在交流伺服系统中用PWM控制产生的等幅不等宽的脉冲序列波来代替正弦波和其他波形,是因为脉冲序列波中有用的是基波成分,而且基波成分越大,这种替代的效果也就越好。

永磁同步电机电压控制方程为

(1)

(2)

力矩模型为

[φiq+(Ld-Lq)idiq]

(3)

机械运动方程为

(4)

1.2 磁场定向控制原理

式(3)的右端表示为由磁链产生的力矩和磁阻力矩,该力矩在电机弱磁高速控制下起到重要作用。一般情况下,控制系统令id=0,此时力矩方程可以写为

φiq

(5)

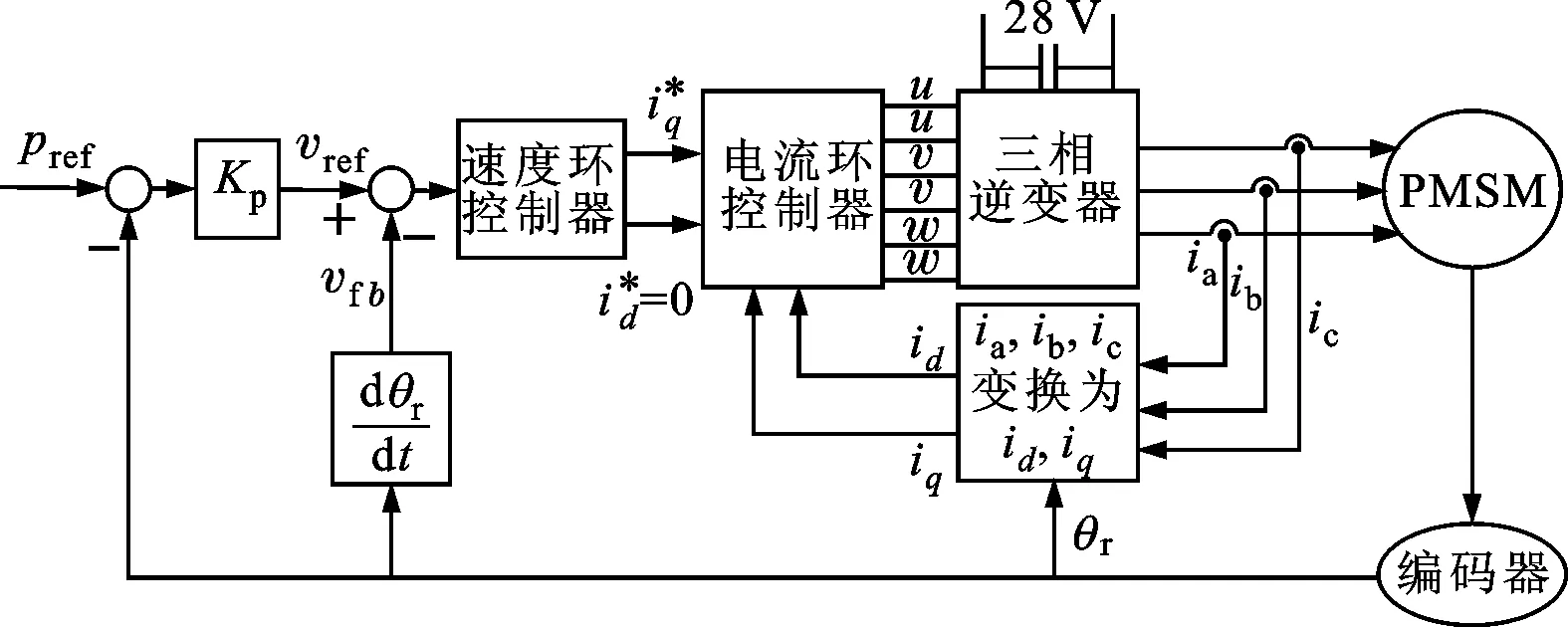
图1 控制系统结构框图

由式(5)可知,系统输出转矩与q轴电流成正比,反馈q轴电流iq的幅值及相位偏差会造成电机转矩输出偏差,影响控制系统的控制精度,并且d-q轴反馈电流值的计算依靠三相电流ia、ib、ic及转轴电角度θe,因此转轴电角度偏差会造成控制系统的空间电压矢量计算偏差。基于式(1)～(5),模型搭建永磁同步电机速度控制系统,框图如图1所示。经过控制系统电流环计算得到6路PWM输出信号,经过功率驱动放大电路将电压输入到电机,驱动电机旋转。

2 基于控制系统模型的双级状态观测器设计

2.1 交流伺服控制时序分析

交流伺服空间矢量计算时序图如图2所示。程序启动①处,首先读取上一个控制周期的模拟值,然后再次启动模拟值,利用该值计算得到的电流值滞后一个控制指令周期,在该控制周期内使用滞后一个控制周期的电流值in-1计算下个控制周期的电压矢量值Un+1。在程序末尾②处执行空间矢量变换,因此空间电压矢量的计算又滞后一个控制周期。

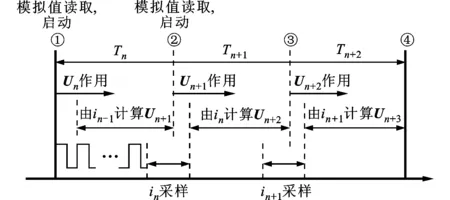
图2 交流伺服控制系统工作时序分析

2.2 电流环状态观测器构造

利用电流状态观测器是解决电流计算时滞问题的有效途径,电压控制矢量方程为

(6)

(7)

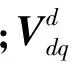
电流状态观测器观测方程为

(8)

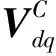
(9)

式中:lc1、lc2为电流环状态误差调节系数。

由分析可知,在程序执行末端电流值滞后电流采样点两个控制周期,将电流观测值的输出再次输入电流状态观测器实现电流时滞的补偿,双级电流状态观测器状态方程可以写为

(10)

2.3 位置环状态观测器构造

在一个控制周期内,转轴加速度u可以认为是恒定不变的,所以电机转子在一个控制周期内的转动角度可以写为

(11)

则电机转轴运行位移及速度微分方程为

(12)

(13)

式中:Te为电机输出转矩;Jm为电机及负载转动惯量;TL为负载转矩。

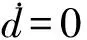
(14)

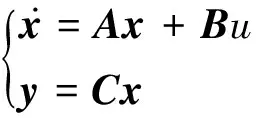
(15)

位置状态观测方程可写为

(16)

因此,电机位置环状态方程可以写为

(17)

位置环离散化状态方程可写为

(18)

式(18)极坐标可以通过调节l1、l2、l3进行任意配置,根据第k周期的观测位移,观测速度及观测加速度扰动值可以估计出第k+1周期的变量值。

由式(14)、式(17)可得观测模型误差方程

(19)

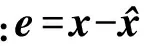
为了保证观测器的稳定性,特征方程的根在复平面的左半部分取值,特征方程为

det[Is-(A-Li)]=0

(20)

特征多项式可为

(21)

由此可得

(22)

状态观测调节系数关系到状态观测器极点坐标的确定,决定着观测误差收敛速度,选择合适的调节系数,令状态误差方程的极点坐标位于复平面坐标系的左半部分以保证状态观测器的稳定性,若想加快状态观测误差的收敛速度,则需将极点坐标配置在距离虚轴尽量远的位置,从而使观测角度快速逼近真实值。根据上述分析可知,该状态观测方程具有明确的物理意义,并且易于实现。

由分析可知,角度计算值存在着一个控制周期的滞后,空间矢量坐标2→3变换时又滞后了一个控制周期,根据式(18),将一级状态观测器的输出作为二级观测器的输入,由此得到的二级观测器离散形式为

(23)

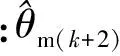
根据式(18)、式(23),构造位置环二级状态观测器结构图,如图3所示。

图3 位置环二级状态观测器结构图

二级位置状态观测器对位置观测的预计能力更强,可消除角度滞后问题,并且具有一定的滤波作用。本文提出的方法相较于文献[11]中的方法更为简单、易于实现,并且解决了文献[8]中位置观测的延时问题。

3 实验结果及分析

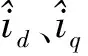
3.1 电流状态观测器实验

对电流环进行阶跃响应测试,给定d轴电流0.5 A,电流环比例增益系数设置为3 000,积分增益系数设置为550,分别应用低通滤波、一级状态观测器以及二级状态观测器得到的电流波形如图5所示。从图中可以看出,低通滤波抑制了电流振荡,但是导致电流反馈信号延时,相反一级状态观测电流不仅抑制了电流的振荡,并且解决了低通滤波造成的延时问题。从实验结果可以看出,电流状态观测器能够准确反映电流真实情况,并且对电流噪声具有明显的抑制作用,而低通滤波器虽然有效抑制高频振荡,但是造成了严重的相位滞后,没有反映当前信号的真实情况。从图5中还可以看出,二级电流状态观测器对电流的预测能力更强,并且二级电流状态观测器在一定程度上消除了一级电流状态观测器的高频振荡问题。如果将电流环状态观测的误差调节增益调节较强,则会引入较强的原始信号噪声,减弱状态观测器的除噪效果,并且由于理论计算和实际系统仍有一定偏差,因此状态观测器仅能对两个控制周期的电流状态进行近似估计。

图4 基于位置环状态观测器的控制系统框图

(a)全图

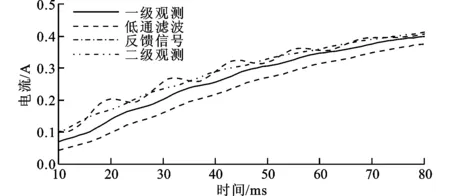
(b)局部视图Ⅰ放大图图5 电流阶跃指令电流响应波形

3.2 位置环状态观测器实验

如图6所示电流环增益系数保持不变,速度环比例增益系数设置为350,积分增益系数设置为100,令电机在450 ms内运行30°,定位500 ms,在450 ms内反向运行至初始点。从实验结果可以看出,位置环状态观测器对角度振荡具有抑制作用,并且准确地反映了当前角度状况。

在相同的运动指令下,引入二级位置状态观测器,观测结果如图7所示。在电机旋转起始段Ⅰ处,可以看出一级位置状态观测器及二级位置状态观测器均对当前角度值进行了准确的估计,并且二级状态观测的预测能力更强。在Ⅱ处,电机定位过程中反馈角度值出现高频振荡,但是一级、二级位置状态观测器对角度振荡起到明显的抑制,消除了反馈位置信号中的高频噪声,并且二级位置状态观测器角度值的预测能力更强。同样,在电机回转时的位置Ⅲ处一级、二级位置状态观测器对电机角度值进行了准确的观测,并且二级位置观测器的预估能力更强。

(a)位置环状态观测全图

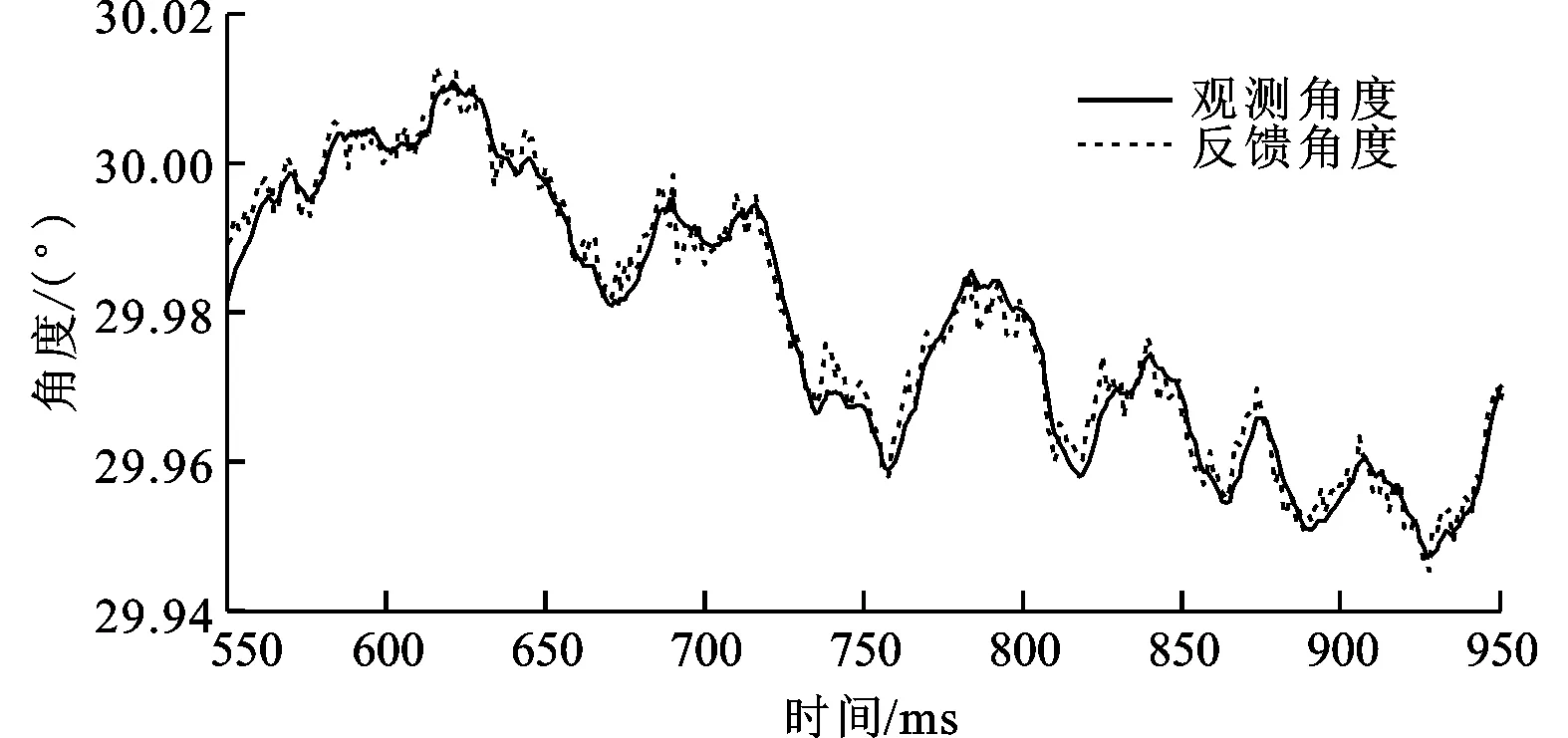
(b)局部视图Ⅰ放大图

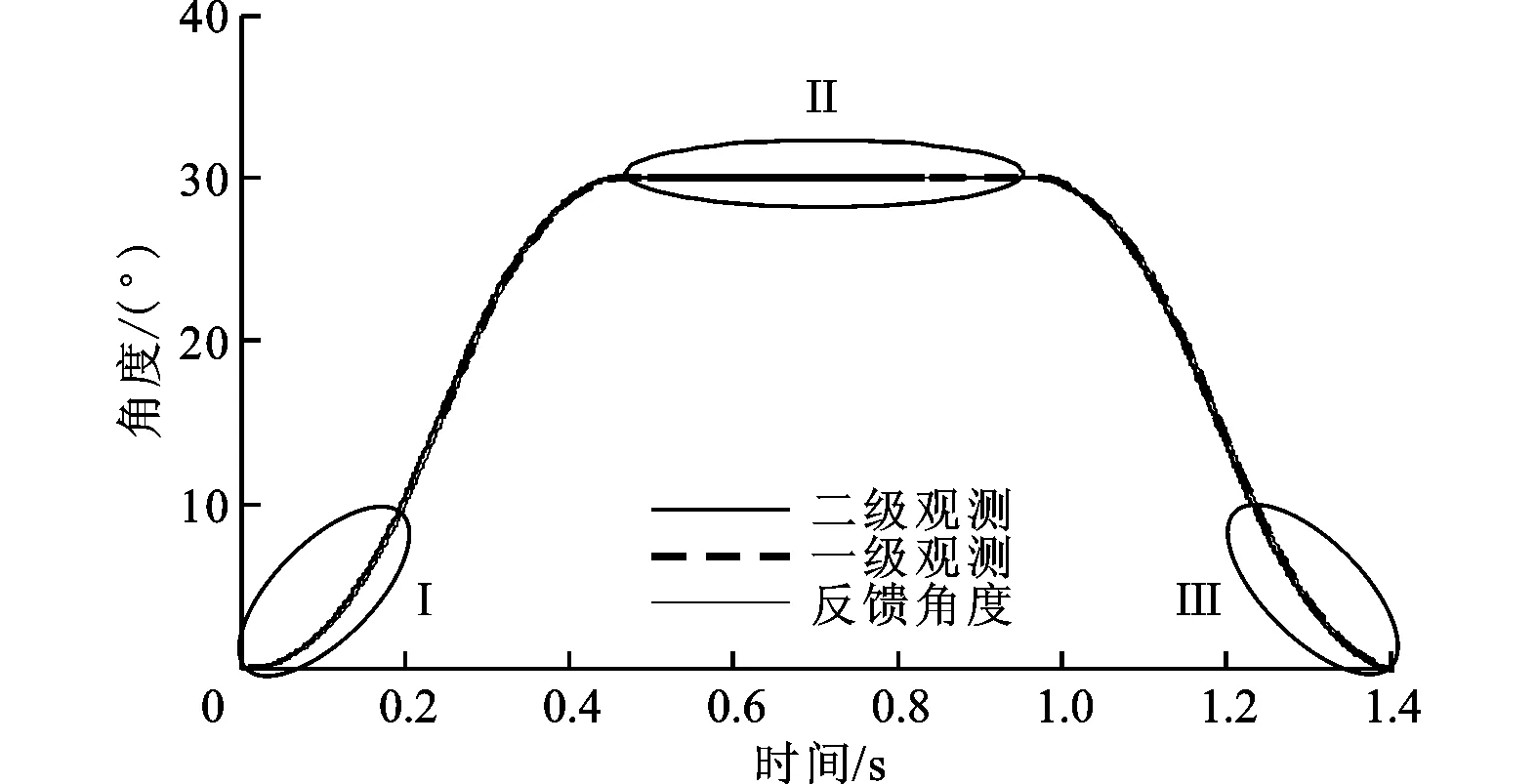
(a)全图

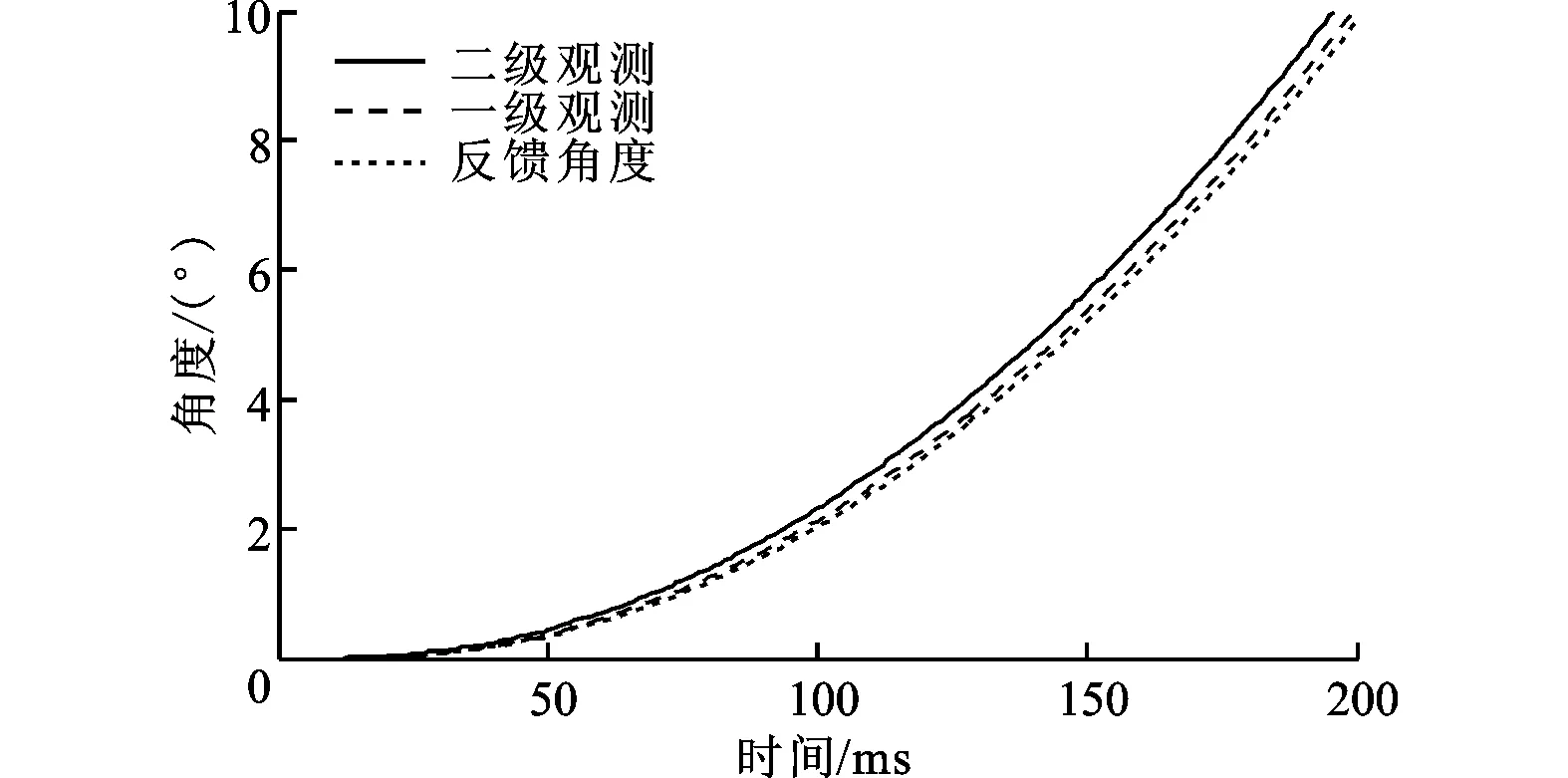
(b)局部视图Ⅰ放大图

(c)局部视图Ⅱ放大图

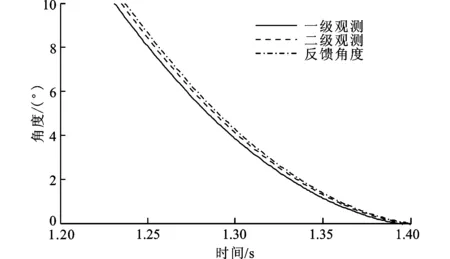
(d)局部视图Ⅲ放大图

3.3 几种角度计算方法的位置误差实验及分析

为了进一步验证本文所提出的状态观测器的有效性,对磁电编码器角度值进行角度观测并进行实验。理想d-q轴霍尔信号为相位相差90°的两路正、余弦信号,如图8所示,利用反正切公式可以计算出当前角度值。

图8 d-q轴霍尔原始信号

实验环境下霍尔安装存在机械偏差,并且每个霍尔的磁敏特性不同,另外给霍尔供电的电源引入了系统噪声干扰,导致两路霍尔信号不是标准正弦信号,由此对d-q轴霍尔信号引入噪声,如图9所示。

当电机转轴以ωm=31.42 rad/s旋转时,使用反正切算法、低通滤波、一级状态观测器以及二级状态观测器的位置输出与标准理想角度输出进行对比。实验中角度低通滤波系数τ=0.000 2 s,一级位置状态观测器误差调节系数l1=330,l2=30 000,l3=1 000 000。二级位置状态观测器误差调节系数l4=115.5,l5=367 5,l6=428 75。4种方法计算出的角度位置与标准理想角度位置误差曲线如图10所示,图10a为利用反正切角度计算公式得到的角度值与理想角度误差曲线。从图10b中可以看出,利用低通滤波方法对角度值滤波可以在一定程度上消除低频抖动,但是造成了恒定偏差值。从图10c可以看出,利用状态观测器对角度偏差的高频噪声和低频抖动均有较好的抑制效果。从图10d可以看出,二级状态观测器对角度偏差的低频抖动抑制能力更强,观测位置偏差小于0.005 rad。

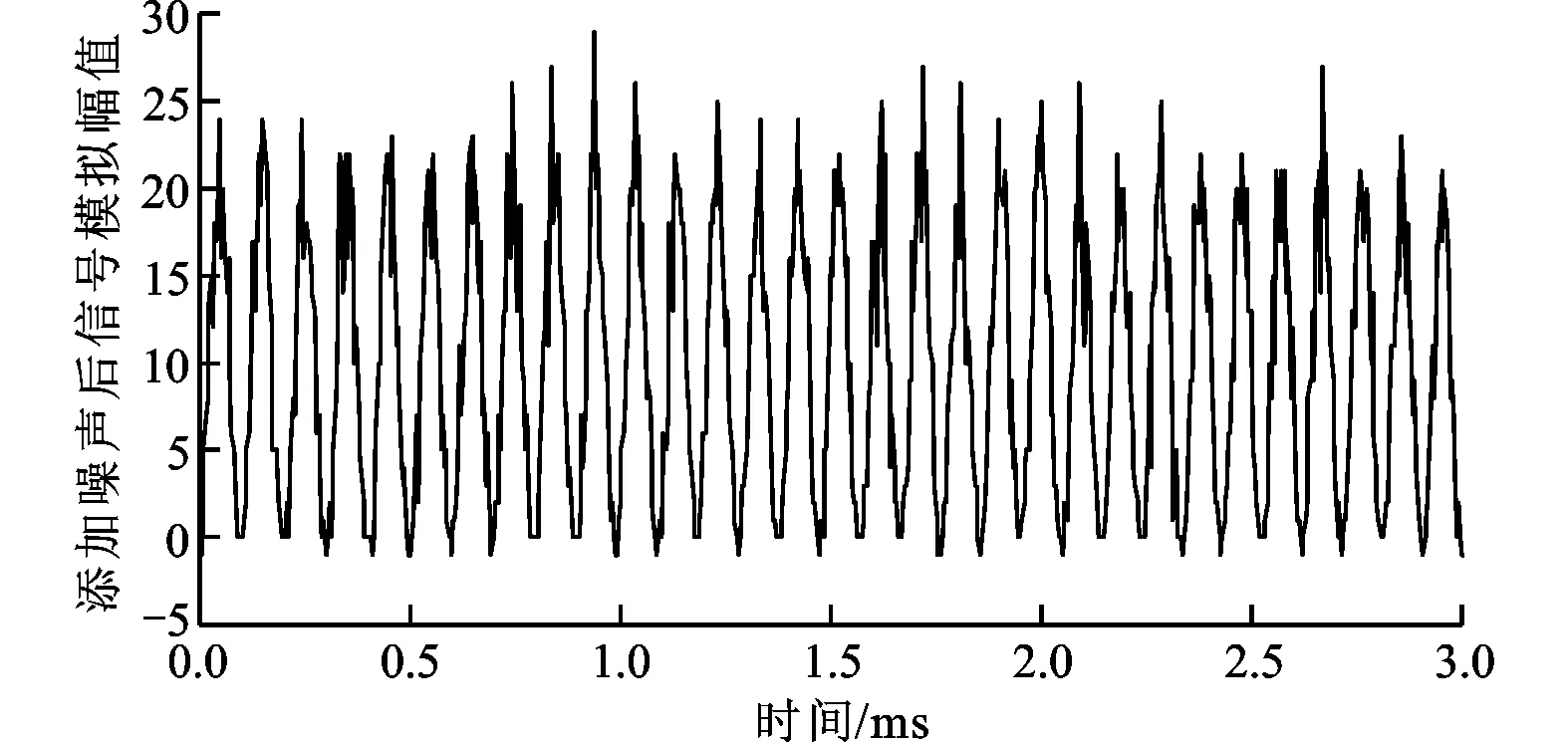
(a)d轴霍尔噪声添加信号

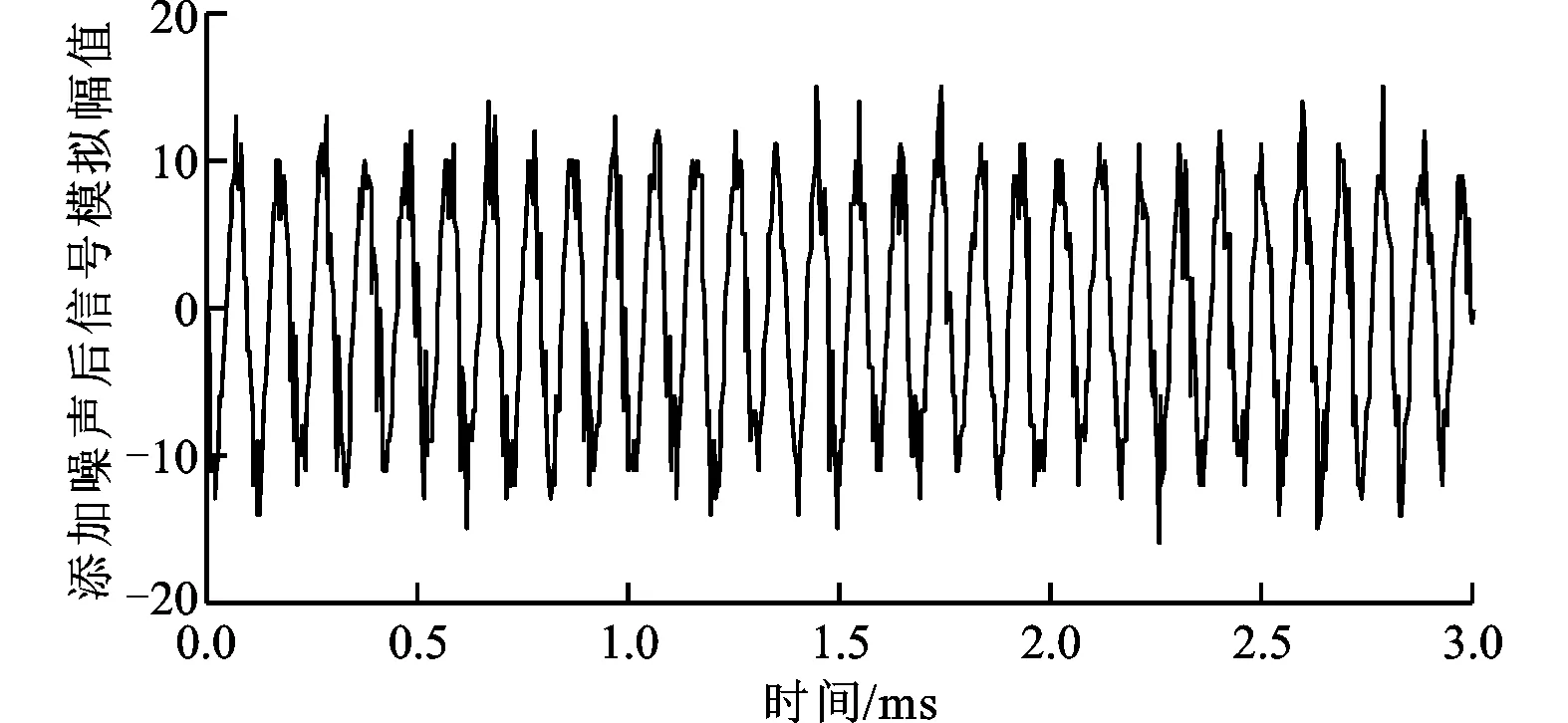
(b)q轴霍尔噪声添加信号

(a)基于反正切算法的角度误差

(b)基于低通滤波的角度误差

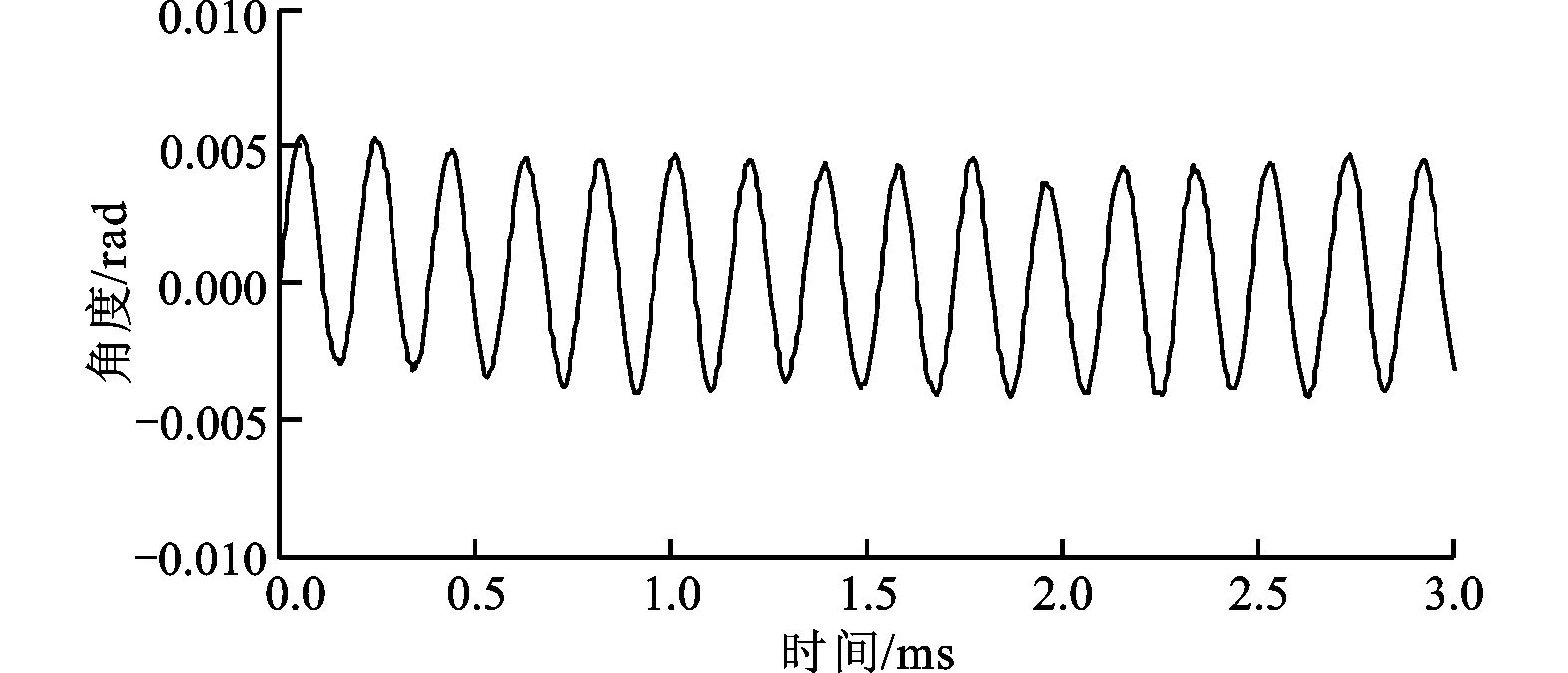
(c)基于状态观测器的角度误差

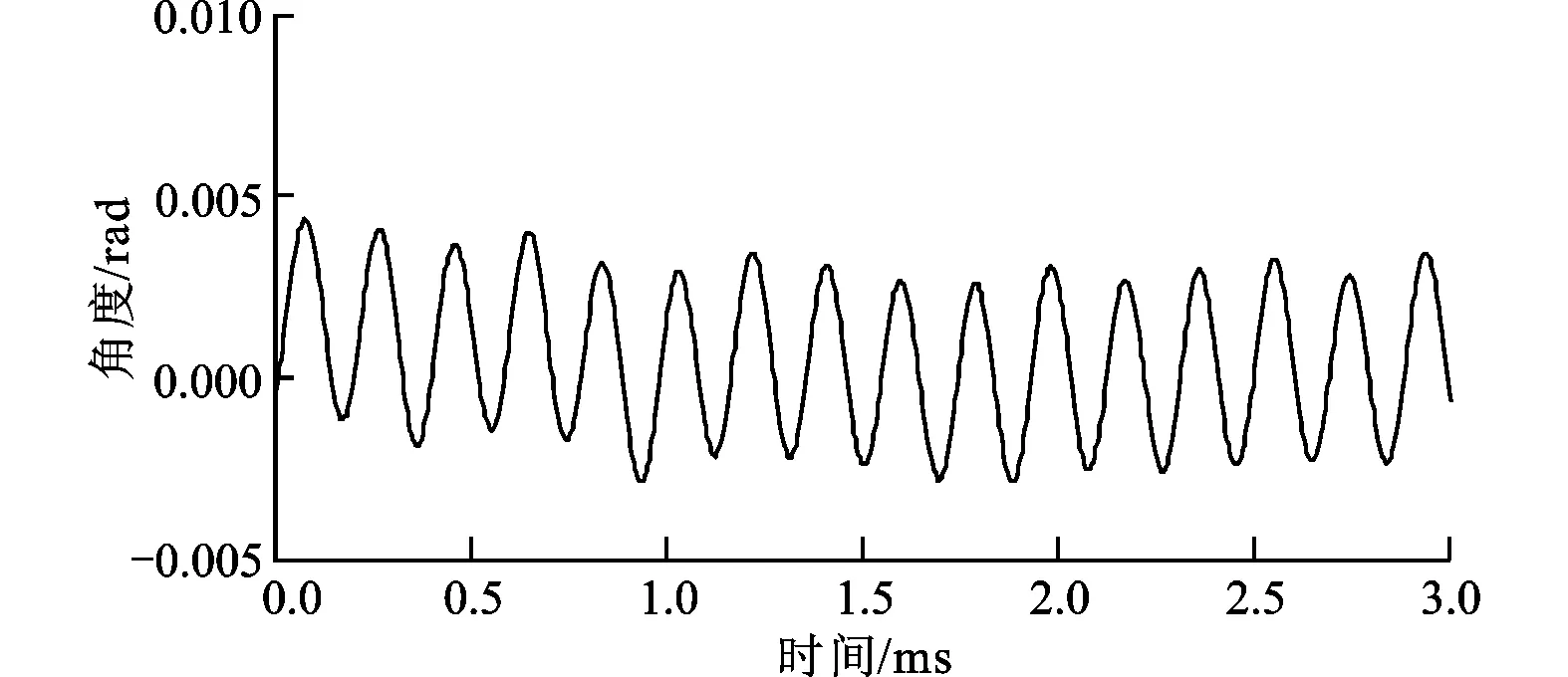
(d)基于二级状态观测器的角度误差

对图10所示信号进行一次微分处理得到图11所示波形,图11b、图11a比较可知,低通滤波抑制了反正切计算角度中夹杂的高频噪声信号。从图11c可以看出,一级状态观测位置信号中的高频噪声被大幅减小,而由图11d可以看出,二级状态观测的高频噪声抑制能力更强。

为了进一步验证本文所提方法的有效性,进行了高响应定位实验,电流环比例增益系数为3 000,积分增益系数为550;速度比例增益为350,积分增益系数为100。在该组增益系数下分别用本文所提方法与传统PI控制器进行高速定位实验。由图12可知,速度指令在5 ms内实现了1 500 rad/min的加减速运动,并在速度指令结束时保持定位状态。

实验结果表明,在指令响应频率达到200 Hz、加速度达到62 831 rad/s2的情况下,传统PI控制器在电机定位控制阶段,相电流振荡较为剧烈,并且最大位置误差达到4°。在相同的系统增益调节参数条件下,采用本文提出的方法,系统相电流振荡得到明显的抑制,位置误差最大为1.5°,定位位置偏差减小,定位过程稳定,证明了本文所提方法的有效性。

4 结 论

本文依据永磁同步电机的电压控制模型及运动模型设计了电流及位置状态观测器。分析控制系统的工作时序可知,控制系统使用的反馈电流及角度存在两个周期的滞后,由此设计了二级状态观测器,并且针对低通滤波除噪法和一级状态观测器以及二级状态观测器的位置误差进行比较。实验结果表明,二级状态观测器不仅具有精确的预测能力,位置观测误差小于0.005 rad,而且有效抑制了检测信号中夹杂的高频及低频噪声。在定位实验中,定位精度达到1.5°,实现了位置及电流的准确观测。

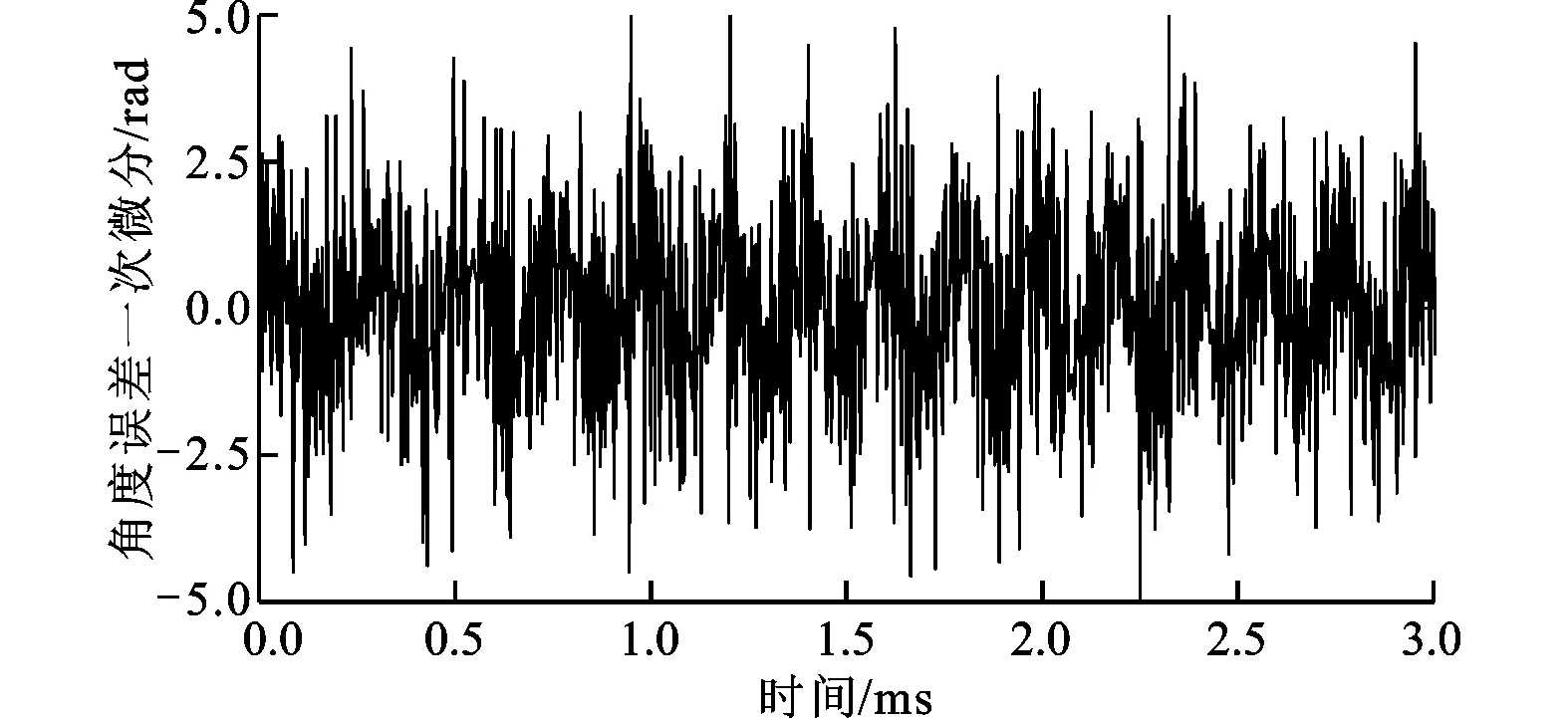
(a)反正切角度误差一次微分

(b)基于低通滤波的角度误差一次微分

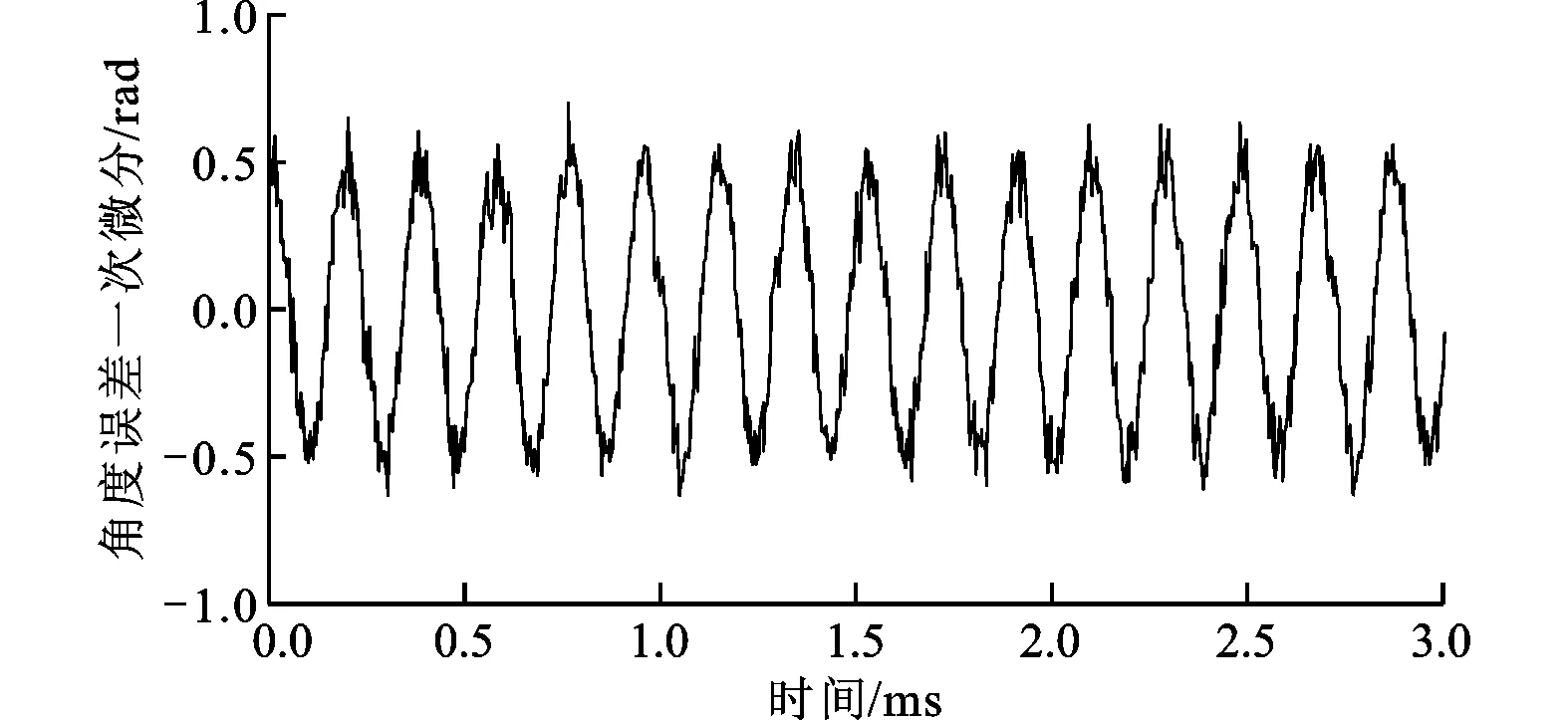
(c)基于状态观测器的角度误差一次微分

(d)基于二级状态观测器的角度误差一次微分

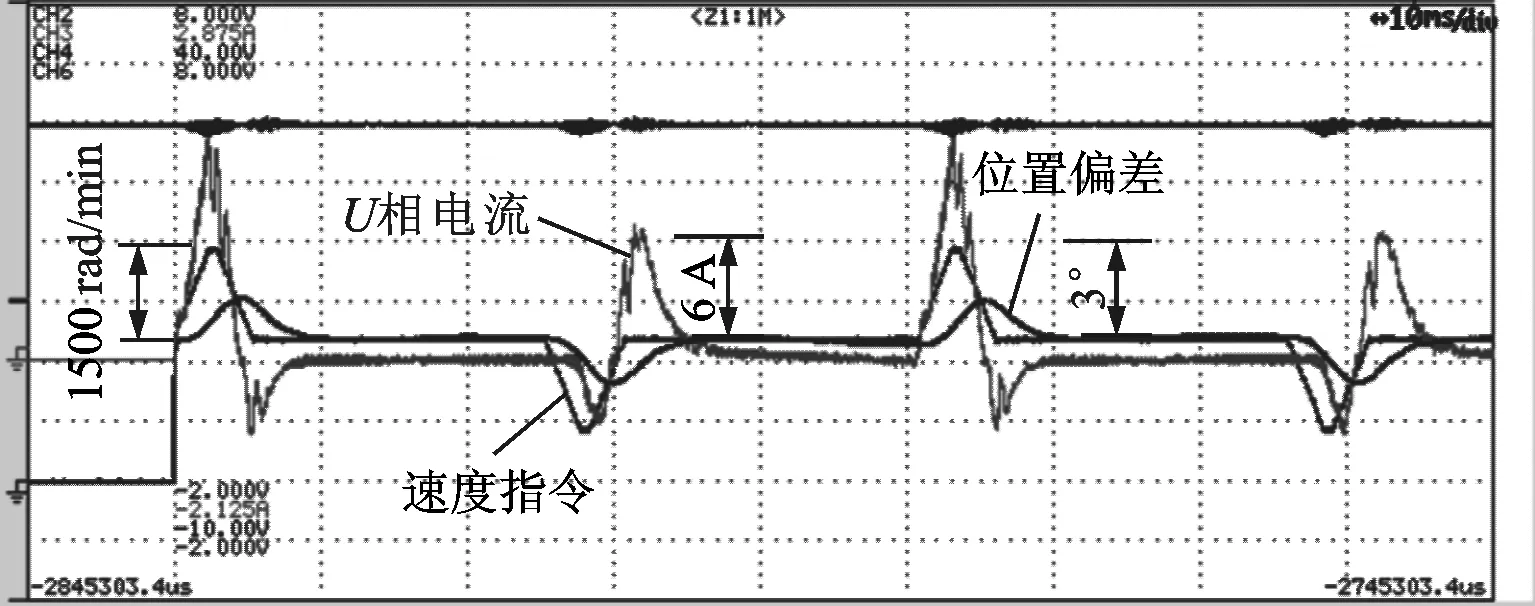
(a)本文方法

(b)传统PI控制方法

[1] 刘文静, 王民慧. 电流检测方法研究 [J]. 传感器世界, 2012(9): 28-31. LIU Wenjing, WANG Minhui. The research on current detection method [J]. Sensor World, 2012(9): 28-31.

[2] 王高林, 张国强, 贵献国. 永磁同步电机无位置传感器混合控制策略 [J]. 中国电机工程学报, 2012, 32(24): 103-109. WANG Gaolin, ZHANG Guoqiang, GUI Xianguo. Hybrid sensorless control strategy for permanent magnet synchronous motors [J]. Proceedings of the CSEE, 2012, 32(24): 103-109.

[3] LUIGI R. Design of a high-performance optical system for angular position measurement [J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(5): 2075-2081.

[4] 黄元峰, 王海峰. 基于DSP的无刷直流电机控制器中电流检测系统 [J]. 电力电子技术, 2011, 45(5): 55-57. HUANG Yuanfeng, WANG Haifeng. Design of current detection system of BLDCM controller based on DSP, 2011, 45(5): 55-56.

[5] 高强, 刘桂花. 一种永磁同步压缩机三相电流重构方法 [J]. 电机与控制学报, 2009, 13(2): 267-271. GAO Qiang, LIU Guihua. Method to three-phase current reconstruction of PMSM compressor [J]. Proceedings of the CSEE, 2009, 13(2): 267-271.

[6] 郝双晖, 刘勇. 基于查表原理的单对磁极编码器研制 [J]. 中国电机工程学报, 2006, 26(19): 165-168. HAO Shuanghui, LIU Yong. Design of single pair-pole magnetic encoder based on looking-up table [J]. Proceedings of the CSEE, 2006, 26(19): 165-168.

[7] 吴忠, 吕绪明. 基于磁编码器的伺服电机速度及位置观测器设计 [J]. 中国电机工程学报, 2011, 31(9): 82-87.

WU Zhong, LÜ Xuming. Design of angular velocity and position observer for servo motors with magnetic encoders [J]. Proceedings of the CSEE, 2011, 31(9): 82-87.

[8] FUERTES J M. Absolute-type shaft encoding using LFSR sequences with a prescribed length [J]. IEEE Transactions on Instrumentation and Measurement, 2008, 57(5): 915-922.

[9] 马雷, 王荣本. 高速智能车辆状态观测器设计 [J]. 吉林大学学报, 2005, 33(2): 174-178. MA Lei, WANG Rongben. State observer design on high speed intelligent vehicle [J]. Journal of Jilin University, 2005, 33(2): 174-178.

[10]王岩青, 姜长生. 中立型线性系统时滞独立状态观测器的设计 [J]. 吉林大学学报, 2006, 44(2): 207-210. WANG Yanqing, JIANG Changsheng. Design of delay-independent state observer for neutral linear systems [J]. Journal of Jilin University, 2006, 44(2): 207-210.

[11]GECKELER R D, FRICKE A. Calibration of angle encoders using transfer functions [J]. Measurement Science and Technology, 2006, 17(10): 2811-2818.

(编辑 赵炜)

Second Level State Observer of Current and Position for Permanent Magnet Synchronous Motor on AC Control System Model

HAO Shuanghui, WANG Lei, SONG Baoyu, HAO Minghui

(School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China)

The voltage control model and the rotor kinematic model of PMSM(permanent magnet synchronous motor) are analyzed to improve the feedback accuracy of servo control system and to solve the delay problem of feedback signal. The analyzing results are further used to analyze the work timing of control system’s feedback loop and the number of hysteretic cycles is obtained. Then, a first level state observer of current and position for PMSM is proposed. The current and position values in the current control cycle are used to obtain accurate estimations of the current and position values in the next control cycle, and the observation output of the first level state observer is served as the input of the second level state observer so that the high frequency oscillation and the time-delay of the current and position’s feedback signal can be further suppressed. Results show that the second level state observer of current and position has a significant inhibition on the high frequency noise and an accurate prediction on the feedback value. The observation error of the second level position is less than 0.005 rad, and the high frequency noise included in feedback has is eliminated. When the proposed method is applied in an AC servo control system for position control with high speed and high response, the response frequency of the system reaches 200 Hz, and acceleration arrives at 62 831 rad/s2, and its positioning accuracy is 1.5, while the system’s phase current is stable. It can be concluded that the proposed method realizes the accurate observation on current and position values.

permanent magnet synchronous motor; voltage control model; state observer

2014-10-21。

王磊(1986—),男,博士生;郝明晖(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(50975057)。

10.7652/xjtuxb201505016

TH-39

A

0253-987X(2015)05-0100-08