平均弹道一致性检验方法分析及改进*
宋艾平,郭晓刚,王益华,熊 伟
(1 63863部队,吉林白城 137000; 2 63867部队, 吉林白城 137000)
平均弹道一致性检验方法分析及改进*
宋艾平1,郭晓刚1,王益华2,熊伟1
(163863部队,吉林白城137000; 263867部队, 吉林白城137000)
摘要:文中针对利用少量样本进行检验造成平均弹道一致性检验判据中正态特性发生变化等问题,利用正态性检验、稳健估计等统计学方法,对试验样本进行了预先检验和数据预处理,重建了检验模型,得出了新的检验方法,并对改进后的检验方法进行了验证,结果表明该方法具有更好的可靠性和适用性。
关键词:弹道一致性;正态分布;正态性检验;M估计
0引言
兵器科学领域对于采用配对t检验[1]验证弹道一致性的方法,普遍对判据合理性、散布和样本量大小以及系统误差选取等因素对检验结果的影响存在质疑[2-3],在试验中也曾发现两弹种未通过弹道一致性检验仍能通过射表检查的案例。文中尝试通过对原始数据进行分析、统计探寻矛盾存在原因,抽取随机数比较计算,以期获得更为科学的检验办法。
1平均弹道一致性检验方法分析
1.1 平均弹道一致性检验方法
目前,按发交叉射击时弹道一致性评定采用如下评定标准[4]:
(1)

检测点若满足下列条件[5],则认为其可作为配对检验观测值。
1)2个不同的满足正态分布的个体,除了检验假设所涉及的系统误差d外,其他所有方面都相似;
2)2个观测值之差满足正态分布。

1.2 存在的问题
1)观测样本的正态性

表1 各口径弹药弹着点坐标正态性统计结果
对各口径弹着点坐标的正态性检验统计结果如表1所示。结果表明平均约10%的数据组不服从正态分布。从正态分布中抽取10 000组随机数,每组7个样本,结果4.38%不服从正态分布。
2)观测样本之差的正态性
对各口径弹着点之差的正态性统计结果如表2所示。结果表明平均约10%的数据组不服从正态分布。从标准正态分布中抽取10 000组随机数,每组7对样本,配对做差,结果4.57%不服从正态分布。

表2 各口径弹药弹着点之差的正态性统计结果
3)对比弹序的选取
在平均弹道一致性试验中发现,利用原有数据,采用剔除首发和末发弹着点数据,即改变对比弹序的方法进行计算,存在与原检验结果不一致的情况。

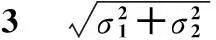
表和σΔ比较的统计结果
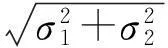
1.3 原因分析
对试验条件及样本量进行分析,产生上述现象原因如下:
1)弹药加工、装配、装填、射击诸元赋予差异以及气象波动造成弹着点存在差异,在数据处理过程中不作任何修正即纳入一致性判据,使抽样样本偏离了正态总体;
2)样本量小,极少数偏离样本数学期望的样本作为典型样本数据混入数据处理,致使样本及样本差值均不能真实反映样本总体及两个总体差所在总体的样本特征。
上述原因造成了弹着点及其差值不满足正态分布、减差时弹序对结果有影响、计算获得的方差不符合正态分布特性等情况。
2平均弹道一致性检验方法的改进
2.1 平均弹道一致性检验模型
根据上述论述,为保证抽样样本满足配对t检验的检验假设,有必要对抽样样本进行以下处理:
1)对抽样样本是否正态进行甄别。
2)对非正态样本,进行样本处理。
非正态样本处理可以通过数学方法弱化异常样本对样本总体的影响或者剔除异常样本两种方法来实现。试验中,除少量离群值外,难以将异常样本与样本其他数据区分开,且剔除异常样本可能造成抽样样本特征的改变,获得错误的估计参数,增加研制方或鉴定方的风险。稳健估计采用对样本数据加权的方法,能在拒绝和接受1个观测值之间起到平滑的作用,既保留了观测值的样本特征,又降低了异常样本特征对参数计算的影响,使其更加接近实际应服从的分布类型。其中M估计[6]用于解决异常样本呈非正态性分布问题具有较好的抵抗异常样本的能力,更适于该类处理。

改进后平均弹道一致性检验模型如图1所示。

图1 平均弹道一致性检验模型
2.2 正态性检验
正态性检验的方法主要有χ2拟合优度检验、柯尔莫戈洛夫检验、W检验、D检验、偏度检验、峰度检验和偏度、峰度联合检验。前两种方法为万能检验方法,对正态性检验不具有特效;W检验适用于样本容量为3≤n≤50的情况;D检验适用于样本容量为50≤n≤1 000的情况。根据Shapiro和Wilk对以上正态性检验的研究,W检验法更适于无方向上偏离先验信息且样本容量较小的弹道一致性试验,即:
假设H0:总体服从正态分布,H1:总体不服从正态分布。
将n个样本测量值按由小到大次序排列为X(1)≤X(2)≤…≤X(n),则有统计量[7]:
(2)
式中:ai(W)为W检验的检验系数;[n/2]为对n/2取整,其中n为样本容量。
给定置信水平α,查表获得ai(W)及统计量W的分位数Wα,计算W,若W M估计的基本原理是在一般极大似然估计的基础上,将异常样本归于随机模型,通过定义某个优化的影响函数来取代最小二乘函数,并根据逐次迭代平差的结果不断的改变观测值的权或方差,最终使异常样本的权趋于0,或方差趋于无穷大,以减小奇异点的影响,具有良好的统计特性和广泛的适用性。对比常用的稳健函数,Huber函数分别基于最小最大偏差准则和最大渐进方差准则,计算量最少,对正态分布数据具有95%的估计效率,同时能有效抵抗奇异点干扰,对于均值和方差的估计具有较好效果[5-6,8]。文中利用Huber位置、刻度函数组成泛函方程组(3)对样本均值和方差进行稳健估计。t、s分别为样本均值和方差的M估计值,取自变量为(Xi-t)/s,c=1.345,β=0.710 1。 (3) (4) (5) (6) (7) 3试验应用 某型弹药2 000m立靶试验中,发交叉射击2组,每组研制弹、对比弹各10发。按式(1)检验发现,高低坐标不满足一致性要求。对研制弹进行通用射表检查发现二者通用射表与检验结果相矛盾。 分别按现行检验方法和改进方法进行计算,结果见表4。分析计算结果,可以获得以下结论: 1)经W检验仅62.5%符合正态分布,利用传统参数计算方法不能获得准确的总体分布参数; 3)改进后方法获得的结果与通用射表检查结果一致。 上述检验结果表明,在样本正态分布比例较小时现行检验方法与通用射表检查结果存在差异,按新模型处理后,更能反映弹着点样本特征,进而获得了与射表检查一致的检验结果。 表4 某型弹药平均弹道一致性检验结果 4结论 文中结合现行平均弹道一致性检验实际应用及随机数抽样计算情况,对配对t检验理论进行深入研究,发现该理论在试验客观条件及小样本的影响下出现样本、对比样本之差不满足正态分布或正态特性等问题,据此提出了用样本正态性检验、M估计、摒弃成对作差的样本预处理方法,建立了新的检验模型,获得了新的检验方法,验证试验证明改进后方法与通用射表检查结论一致,具有更高的可靠性和适用性。 参考文献: [1]闫章更. 试验数据的统计分析 [M]. 北京: 国防工业出版社, 2001: 97-118. [2]董满才, 刘云南. 弹道一致性检验若干问题的辨析 [J]. 弹箭与制导学报, 2011,31(4): 152-154. [3]王声生. 弹道一致性试验判据的分析与建议 [J]. 四川兵工学报, 2011(10): 64-66. [4]GJB4225-2001 榴弹定型试验规程 [S]. 2001. [5]张领科, 王中原, 王枫. 弹道一致性检验准则应用中的问题分析和建议 [J]. 弹道学报, 2005, 17(4): 17-21. [6]王家帮, 脱立文, 吴友平. M估计的权函数选取及其抗差性比较 [J]. 山西建筑, 2008, 34(13): 351-352. [7]梁小筠. 正态性检验 [M]. 北京: 中国统计出版社, 1997. [8]王声生. 基于稳健估计的弹道一致性试验方法 [J]. 舰船电子工程, 2011, 31(11): 132-135. 版 权 声 明 凡稿件被本刊录用,即视为作者同意将该论文的复制权、发行权、信息网络传播权、翻译权、汇编权等权利在全世界范围内转让给本刊。本刊已许可中文科技期刊数据库(维普)、万方数据数字化期刊群和中国知网(中国学术期刊(光盘版)电子杂志社)在其各自的系列数据库产品中以数字化方式复制、汇编、发行及在信息网络传播本刊全文。作者著作权使用费和稿酬一并支付(即包括印刷版、光盘版和网络版各种使用方式的报酬)。如作者对本声明持有异议,请在投稿时说明。 本刊编辑部 收稿日期:2014-11-08 作者简介:宋艾平(1979-),女,吉林白城人,硕士,研究方向:弹药鉴定。 中图分类号:TJ4 文献标志码:A The Analysis and Improvement on Test Method of the SONG Aiping,GUO Xiaogang,WANG Yihua,XIONG Wei (1No.63863 Unit, Jilin Baicheng 137000, China; 2No.63867 Unit, Jinlin Baicheng 137000, China) Abstract:Aiming at the question of the test criterion of average trajectory consistency, it thinks out that small sample is the reason of normal characteristic’s charge. The pretest and data pretreatment is give with normality test and robust estimation for test sample. It rebuilds a test model and obtains a new test method. According to the testing result, the method has high applicability and reliability. Keywords:the average trajectory consistency; normal distribution; normality test; M-estimation2.3 M估计


Average Trajectory Consistency

